助力幼小衔接的数学学习任务设计

2022年版课标提出：“注重幼小衔接，基于对学生在健康、语言、社会、科学、艺术领域发展水平的评估，合理设计小学一至二年级课程，注重活动化、游戏化、生活化的学习设计。”同时要求“关注幼小衔接，帮助学生积累数学活动经验”。那么，我们如何从数学学习角度做好幼小衔接工作，帮助儿童更好地适应小学课堂教学呢？下面几位老师从不同角度进行阐述，并用不同方式进行了尝试。到底哪一种方式更好呢？阅读了这个“幼小衔接研究专辑”，也许您会有不一样的思考，也期待您将自己的研究成果写成文章与大家分享。

幼儿园与小学教育中都涉及数学学习内容，其目标与学习方式既有区别又有联系，厘清这些区别与联系是做好幼小衔接的关键点，抓好联系是落实幼小衔接的根本。幼儿园与小学一年级数学教学中的联系点是根据五六岁儿童的认知特点，设计充分调动他们动手动脑、有趣好玩的探究性学习任务（活动）。本文所呈现的探究性学习任务既适合幼儿园大班学生，也适合小学一年级学生，落实的活动方式、目标要求略有不同。助力幼小衔接的数学学习任务或活动主要有如下几类，这些任务主要来源于一线教师的教学实践以及改编自剑桥大学NRICH（https：//nrich.maths.org）项目中的题目。

一、制作类的探究性、实践性活动

婴儿从一出生就开始用身体认识世界，身体在认知的实践中发挥关键作用。实践性活动给学生带来亲身参与学习活动的机会，是幼小衔接重要的联系点。

（一）实践性活动：跳格子。

活动方式一：在操场或教室地面上画一条数线。数线上的数让学生自己标，可以是百以内的任何一个区域的数。（如图1）

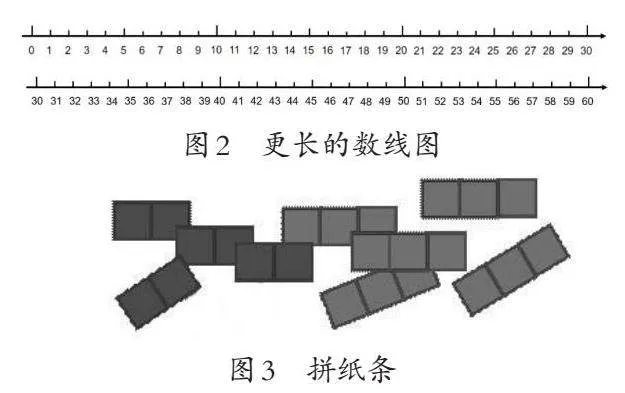
活动方式二：请学生在数线上（如图2）边跳边数。可以按照下面的规则进行，也可以按照自己的规则进行。

（1）从0开始，从左往右，每次跳2个格子，跳5次。

（2）从10开始，从右往左，每次跳2个格子，跳5次。

（3）任选一条数线，任选一个数，从左往右，每次跳5个格子，跳5次。

活动方式三：在地面上画一条数线，从0到100标上数，做更具挑战性的活动。

投两次骰子，第一次投出的结果是起始数的十位，第二次投出的结果是起始数的个位，然后得出一个起始数。如第一次投骰子结果是2，第二次投骰子结果是3，则起始数为23。接下来，从起始数所在的点开始，向左或者向右移动5次，使最后所在的点尽可能接近50。同时要注意，每次移动的距离只能是1、10、100。如当起始数是23时，可以先向右移10格到33，再向右移10格到43，再向右移10格到53，向左移1格到52，再向左移1格到51。

和同伴们试一试，并且比一比你们的策略。你是否最终正好到达50？你最终和50差了多少？你有没有想出多种方法？哪些初始数可以让你正好到达50？哪些初始数没办法让你到达50？

在蹦蹦跳跳的活动中，学生不仅有身体参与还有思维参与，用到了不同的数数方法，感受到在数线上，从左往右数越来越大，从右往左数越来越小，往右跳就是几个几个地加，往回跳就是几个几个地减，背后还有对乘法与加法、除法与减法的关系的孕伏。小学数学的重要内容应该自然地卷入儿童熟悉的肢体活动中。

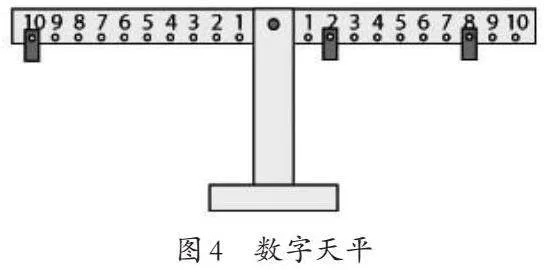
（二）拼纸条。

活动准备：两人一组用小方块拼成一些纸条，一个人用两个红色小方块拼成一条红色纸条，另一个人用三个蓝色小方块拼成一条蓝色纸条。多做一些。（如图3）

活动要求：分别用自己做的纸条首尾相接排成一列，拼成了一条长纸条。想一想：两个人能不能拼出两条相同长度的长纸条呢？在拼成相同长度的长纸条时，你们分别用了几条纸条？这时这两条长度相同的长纸条有多长呢？除了这个长度，还有没有拼出别的长度的可能呢？

学生在熟悉的拼接活动中把图形的个数和长度结合起来，通过比较、反思理解单位和长度之间的关系，简单的活动过程蕴含小学数学中重要的思想方法。

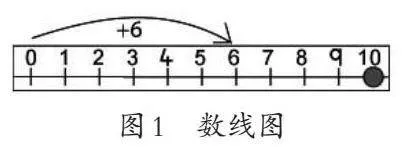
（三）好玩的数字天平。

有一个数字天平（如图4）以及很多个质地相同的数字砝码。在天平左侧“10”的位置放上1个数字砝码时，要想使天平保持平衡，你可以：

①在天平右侧“10”的位置也放上1个数字砝码；

②在天平右侧“1”的位置放10个数字砝码；

③在天平右侧“2”和“8”的位置分别放1个数字砝码。

想一想，如果左侧“10”的位置放了1个数字砝码，那么在右侧放置什么样的砝码才会使天平保持平衡呢？你有几种方法？

如果左侧“3”和“4”的位置各放置了1个数字砝码，右侧“2”的位置放置了3个数字砝码，需要在右侧怎样增加砝码才能使天平保持平衡？

数字天平的工作原理与天平类似，两边相等就会平衡，不过在数字天平中，要求相等的是两个算式的和（包括数与数、数与式），这是帮助学生建立相等关系的绝妙工具。学生从直观的“同数即等式”到“等值即等式”，通过数字天平初步理解等式，培育代数思维的萌芽。

二、有规律的数数与计算

学生对数学的认识往往是从数数开始的，数数中也确实蕴含丰富的规律，这些规律与计算有千丝万缕的联系。

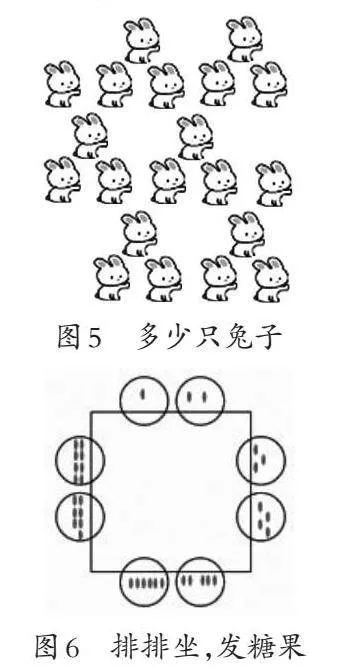
（一）数兔子。

图5中有多少只兔子？圈一圈（摆一摆）、数一数。你有几种数的方法？

数数对于儿童来说是很熟悉的活动，对数数方法的关注则让他们的思考深入小学数学的学习中。不同的数数方法与小学数学的核心概念“计数单位”相对应，同时为乘法与“倍”的关系的学习埋下了伏笔。

（二）排排坐，发糖果。

活动准备：在一次聚会上，你和七个朋友围着桌子坐下。

活动要求：坐在上边左侧的是主持人，他有一袋糖果，准备从他开始按照顺时针方向给所有人发糖：第一个人（他自己）发1颗糖，第二个人发2颗糖，第三个人发3颗糖，以此类推。

方式一：选好你的位置，然后思考下面的问题。

你和对面那个人加起来有几颗糖？桌子每一边的两人一共得到几颗糖？你和斜对面的那个人加起来有几颗糖？

方式二：想象有一张更大的方桌，桌子每边可以坐的人更多。比如，每边分别坐三人、四人和五人时，某个人和对面那个人加起来有几颗糖？桌子的每一边各需要发几颗糖？某个人和斜对面的那个人加起来有几颗糖？

同时，想一想：如果是五边形或六边形的桌子，情况会怎样呢？

起初学生可能只是根据活动中的信息做简单的加法口算，随着口算的进行，学生会逐步关注和的变化和加数的变化之间的关系。

（三）口算小玩具中的规律。

对于计算内容的教学教师们研究得比较多，但是要想让学生基本的口算技能过关并非易事。枯燥的练习给学生带来了烦恼，我们可以给口算练习穿上游戏的外衣，让学生在玩中练起来。

方式一：做个数字小转盘，（如图7）把9放在中间，转动转盘玩一玩，转到哪里快速说出得数。

方式二：做个加法运算滚筒，（如图8）和同桌玩一玩。

这样的游戏活动通过游戏的思维和机制，让儿童乐于参与学习，实现数学知识的再创造。游戏过程中，儿童的四肢、情感、大脑共同参与，也是实践、感知、思考的交互作用，关注了学生的身体认知。“身体的经验在情境的展开中获得实现，教师或学生在这种情境中体验到与知识接触的快乐，体验到身体的意志和归属。情感的心智和理智的心智在这种情境中双双获得成长”[1]，游戏化活动使学生的学习增添许多自我感受，也获得学习数学的自信心，为学生的后续学习积蓄了能量。

三、将数学与自然科学相融合的探究性任务

在幼儿园阶段，幼儿学习的学科界限不明显，儿童主要是在生活中、在认识自然界的过程中学习，对大自然的向往与好奇是保持学习愿望的动力。小学阶段设计数学与自然科学融合的探究性任务，不仅可以关注到学生学习的兴趣，而且从跨学科的角度考虑，还有利于学生综合素养的发展。

（一）动物运动会。

一天，花园里的五只小动物准备办一次运动会。五只小动物分别是：长长的、爱睡觉的毛毛虫，整天忙忙碌碌的瓢虫，长着长腿的蜘蛛，能跳得很高的青蛙，全身黏糊糊、行动迟缓的蜗牛。

它们准备进行四场比赛：游泳、赛跑、跳高和跳远。同学们，你们觉得每场比赛的获胜者分别是谁呢？你们判断的依据是什么呢？

第二天，几只小动物又想办一次运动会，可是毛毛虫在家里睡觉，一直都没有醒来。青蛙说：“等它过几天醒了之后，我们再办运动会吧！”其他三只小动物纷纷赞同。

过了几天，毛毛虫从睡梦中醒来，变得和以前大不一样。同学们猜一猜，毛毛虫发生了什么变化？

小动物们准备再办一次运动会，这次同样有四个项目：游泳、赛跑、跳高、跳远。这一次同学们觉得每场比赛的获胜者分别是谁呢？毛毛虫的变化会给比赛结果带来什么改变呢？你们判断的依据是什么呢？

根据动物的生物特点确定运动会各项目的成绩，甚至蝴蝶的羽化过程也融入问题情境中，自然科学与数学的有机融合为学生适应期的学习减缓了坡度。

（二）幼儿版鸡兔同笼问题。

鸡兔同笼问题是我国古代的数学名题。大约1500年前的《孙子算经》中记载了这个有趣的问题，学生具备一定的知识储备之后会有多种解决问题的方法。虽然处于入学适应期的学生还不能解决这样的问题，但是我们可以让学生思考相关的数量关系，融入小动物的身体结构的问题会激发学生的探究热情。

探究一：每种动物有几只？

小鸡、小鸭、刺猬和小狗去坐小火车。小明看见座位上一共有12条腿。他看到的可能是哪些动物呢？你能想到几种可能的搭配？你是怎样找到答案的？

探究二：每种瓢虫有几只？

花园里有两种瓢虫，一种是七星瓢虫，另一种是四星瓢虫。

小杰和小米看到一片叶子上有3只瓢虫。

小杰说：“一共3只瓢虫，2只四星瓢虫和1只七星瓢虫。”

小米看了看说：“那就是说它们的身上一共有15颗星。”

小杰听完，有了新问题：“几只瓢虫加起来会有16颗星呢？”

小米跟着问：“什么情况下几只瓢虫加起来会有14颗星呢？”

你能解决他们两个人的问题吗？你发现了几种可能的情况？

用4和7可以组成多少种可能的结果？在4至35之间，哪些数可以组合出来，哪些数无法组合出来？

学生可以根据对小动物身体结构的了解，根据某种小动物的腿数和瓢虫身上的点子数进行尝试。从无序试误到有序思考，学生的生活经验会逐步数学化，不知不觉进入数学内部，把握数学的学习方法。

参考文献：

[1]叶浩生.具身认知：认知心理学的新取向[J].心理科学进展，2010，18（05）：705-710.

（作者单位：北京教育学院数学系，北京市东城区教育科学研究院，吉林敦化市黄泥河镇中心小学）