在抽象中建模，在运用中理解

【理念解析】

加法数量关系是2022年版课标在第二学段“数量关系”中新增的内容，旨在帮助学生在理解四则运算含义的基础上，逐步认识并掌握“总量等于各分量之和”这一加法模型的本质。基于对课程标准的分析和教学内容的特点，在设计本节课时，我们努力做到如下几点：

1.激活学生已有的生活经验。学生的已有经验是抽象模型的基础。数学建模的起点是用数学的眼光观察生活情境并发现和提出问题。因此，本节课基于学生的生活经验，在学生的生活背景中甄选数学素材，激发学生提取加法模型的逻辑雏形，引领其在真实情境中揭示数学本质，自主建构加法模型。

2.引领学生完整经历抽象数学模型的过程。抽象的过程表现为以下三个步骤：首先，依托对加法的原始理解，抽象出具体的数量关系式；其次，抽取具体数量关系式的共同点，进行儿童化的本质表述；最后，从儿童的表征出发，概括出加法数量关系，完成模型的抽象。这样遵循儿童认知规律的学习过程，有助于发展学生的模型意识。

3.在运用模型中培养学生的数学应用意识。在教学中利用典型实例，让学生感受数学模型可以用来解决一类问题，认识到现实生活中大量的问题都与数学有关，进而感受数学的价值，激发学生主动用数学眼光观察现实世界，主动运用数学原理解释现象和解决问题的意识。

【教学过程】

一、激活经验，丰富研究素材

师：同学们，你们知道南京的紫金山天文台吗？我们一起来感受一下。

（课件播放紫金山天文台的视频介绍）

师：（出示图1）上个周末，三（1）班的同学到这里开展了一场研学活动，还发现了三个数学问题。

师：你会列算式解决这三个问题吗？

（学生逐一解决问题，然后汇报算式）

【设计意图】从学生熟悉的生活场景出发，唤醒学生关于加法的已有经验，自然地引出三个加法实际问题并将其作为研究素材。这三个加法问题涵盖了三种不同的加法类型——合并、添加、减法逆运算，拓宽了加法模型的外延。

二、自主建构，经历建模过程

1.解决问题，抽象数量关系式。

师：这三个问题各不相同，为什么都用加法解决呢？先来看第一题，说说你的想法。

生：要求星期六上午的人数，就是把星期六上午中小学生的人数和星期六上午成人的人数合起来。

师：是的，星期六上午的人数=星期六上午中小学生的人数＋星期六上午成人的人数。（板书）这就是第一个加法问题的数量关系。对于第二题和第三题，你也能像这样说一说它们的数量关系吗？先和同桌互相说一说，再交流汇报。

师：谁来说给大家听听？

生：原来的个数=卖出的个数＋还剩的个数。

生：现在的人数=原计划的人数＋增加的人数。

（黑板上相机呈现以上两个数量关系）

师：同学们，生活中像这样的加法问题还有很多，谁会自己编一个加法问题？

（学生自主列举一些生活中的加法问题）

师：对于生活中的加法问题，你们都能说出像刚刚那样的加法数量关系吗？（生：能）这样的加法数量关系说得完吗？

生：说不完。

2.自由表征，尝试归纳。

师：仔细观察这些加法数量关系，它们有什么共同特点呢？你能用一个式子或一幅图把它们的共同特点表示出来吗？

（学生活动，自主表征）

师：老师收集了几幅有代表性的作品，我们一个个来看。

师：（呈现①号作品，如图2）这是什么意思呢？谁上来介绍一下？

生：○表示那些数量关系等号左边一共的数量，△和□是等号右边的两个部分。

师：看来，这样一幅简洁的作品真能把它们的共同特点表示出来。

师：第2幅和第3幅（图略），也是这个意思吗？谁再来说说看？

师：原来，这三幅作品虽然看上去都不相同，但本质上是一样的。

生：都表示总的数量等于一部分加另一部分。

师：（呈现②号作品，如图3）我们聚焦用文字表示的②号作品。

师：一共的个数，在数学上有一个特殊的名字，谁能猜猜？

生：总数。

生：总和。

生：总量。

师：同学们，你们的感觉是对的！其实就叫作总量，一个部分叫作分量，另一个部分也叫作分量。

师：这三者之间是什么关系呀？

生：总量＝分量＋分量。

师：理解什么是总量和分量了吗？在刚刚这些作品里，能看到总量和分量吗？

（学生分别指一指每幅作品里的总量和分量）

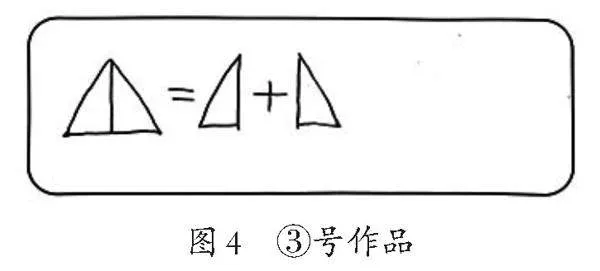
师：（呈现③号作品，如图4）在③号作品里，如果去掉等号后面的部分，还能看到总量和分量吗？

生：能，整个三角形部分就是总量，左边是分量，右边也是分量。

师：真有数学眼光，会思考！如果把这个三角形换成椭圆，还可以表示总量与分量之间的关系吗？

生：可以。

师：这个椭圆就是——（出示加法模型的集合图，图略）

生：总量。

师：这两个部分是——

生：分量和分量。

师小结：刚刚我们在解决问题的过程中，发现了这些数量关系，找到了它们的共同特点，还用这样一幅简洁的图表示。这就是我们今天研究的加法数量关系。（揭示课题：加法数量关系）

【设计意图】通过核心问题“为什么都用加法计算”的回应，引导学生在解释用加法计算的道理的时候，规范地说出具体的数量关系。接着，列举生活中的加法问题，为接下来的观察、对比、分析、概括加法数量关系，积累更丰富的素材。然后，鼓励学生自主表达对数量关系共同特点的理解，用一个式子或一幅图，尝试自主表征，完成儿童化的抽象。最终在交流讨论中，共同完成加法模型的抽象。这样的设计符合学生的认知特点，充分发挥了他们学习的主观能动性。

三、运用拓展，感悟模型价值

1.感受分量与总量之间的关系。

（1）感悟分类标准不同，分量也不同。

师：同学们，让我们带着对加法的新认识继续解决问题。根据表格中的信息，你还能提出哪些加法问题？

师：“紫金山天文台星期六一共有多少人参观？”你会用今天我们研究的加法数量关系解决这个问题吗？为了便于研究，老师带来了这样四块彩板分别表示表格中的四个数据。

（黄色的，黄色加条纹的，红色的，红色加条纹的，四块彩板分别对应贴到如图1的表格中）

师：这四块彩板分别表示什么意思？

师：你能用这些彩板，在这幅图里摆一摆（贴上空白的集合图，图略），表示出这个复杂问题中总量与分量之间的关系吗？

（学生摆，然后展示交流不同摆法，如图5）

师：同一个总量，为什么会有不同的分量？

生：一种是按照星期六上午和下午来分的，一种是按中小学生和成人来分的。

师：同学们总结得太棒了！分类标准不同，同一个总量会产生不同的分量。

（2）感受“此分量是彼总量”。

师：“星期六上午的人数”在这里是什么量？在上一个问题中又是什么量呢？

生：“星期六上午的人数”在这个问题里是分量，在上一个问题中是总量。

师：为什么一会儿是总量，一会儿又是分量呢？

生：因为每次的问题不同，它所扮演的角色也不同。

师：同一个量，有的时候是分量，有的时候是总量，需要具体问题具体分析。

2.感受加法与减法之间的关系。

师：“星期六上午的人数”在第一个问题里是总量，求总量我们用的是什么方法？

生：求总量，用加法计算。

师：那如果求分量，该怎样求呢？

生：分量=总量-分量。

师：真会推理！你能根据分量=总量-分量这样的关系，把这道题（指图1左下角关于望远镜的题）改编成求分量的减法问题吗？

生：原来有36个望远镜，卖出24个望远镜，还剩多少个？

生：原来有36个望远镜，卖出了一些，还剩12个，卖出了多少个？

师：看来今天所学的加法数量关系，不仅能解决加法问题，也能解决减法问题。

3.感受模型的普适价值。

师：（出示图6）“三（1）班有多少人？”你能从老师带来的信息中选择两个合适的条件，并解决这个问题吗？

出示活动要求：

①想一想：可以选择哪两个条件呢？

②填一填：把所选条件的序号填入图中的框里，并列式计算。

（ ）＋（ ）＝（ ）（人）

③说一说：把什么看作总量，把什么看作分量？

师：谁愿意和大家说一说你是怎么选的？

生：我选的是①号和⑥号。

师：选择“三（1）班比三（2）班多4人”和“三（2）班一共有35人”这两个条件时，想一想，是把什么看作总量，谁是它的两个分量？

（借助线段图帮助学生突破难点，明确分量）

生：三（1）班和三（2）班相等的人数是一个分量，比三（2）班多的人数是另一个分量。

师：还可以怎么选？

生：我选②号和④号。

师：这个时候，分量是谁呢？

生：前三组每组有10人，算出前三组共多少人，这是一个分量，第四组人数是另一个分量。

师：原来，把前三组每组10人，看成一个整体，也是一个分量。

师：为什么“三（1）班周三下午有16人参加舞蹈组”“三（1）班周三下午有10人参加体育组”这两个信息没有选？

生：因为这两个部分加起来不等于总人数，应该还有别的组。

师：那样的话，你觉得会有几个分量呢？

生：可能是三个、四个，或者很多个。

师：可是今天学习的加法数量关系式“总量＝分量＋分量”，为什么只有两个分量呢？

小结：总量里的分量可以有若干个，无论多少个，都是把所有分量相加得到总量。

【设计意图】初步概括出加法数量关系后，带着加法模型进一步应用解决问题，让学生在初步运用和相互交流的过程中加深对加法数量关系的理解，进一步感受加法数量关系在分析与解决问题中的价值。在具体情境中，感受分类标准对分量的影响以及理解“此分量是彼总量”；进一步拓宽加法模型的外延，感受虽然数量关系式和图中看起来都只有两个分量，但实际上总量里可以是三个分量，也可以是四个分量，甚至若干个分量。

四、回顾整理，总结提升 （略）

（作者单位：南京师范大学附属小学）