“乘法口诀尾数的对称性”教学实录及赏析

【教学目标】

1.进一步认识乘法口诀和对称性，掌握乘法口诀尾数对称性的特点。

2.在经历探寻乘法口诀尾数对称性的过程中，感悟数形结合思想，积累基本数学活动经验，发展空间观念和推理意识。

3.体会数学与其他学科知识之间的联系，感悟数学在生活中的作用与价值。

【课堂实录】

一、导入

师：今天这节课我们一共要研究五个问题。（课件出示：1.关于乘法口诀。2.关于尾数。3.关于对称。4.关于乘法口诀尾数的对称性。5.关于本节课的意义）下面就先研究第一个问题。

（一）关于乘法口诀。

师：乘法口诀我们大家都很熟悉，你能说一句吗？

四个学生分别说出：四八三十二，九九八十一，三八二十四，七七四十九。

教师依次板书：4×8=32，9×9=81，3×8= 24，7×7=49。

师：乘法口诀有很多，说得完吗？

生：（随口回答）说不完。

师：（笑了）不要老师一问“说得完吗”，大家就马上回答“说不完”。要动脑子，其实口诀就那么几句，当然说得完。好了，第一个问题解决了，就叫作乘法口诀，难吗？

生：不难。

【赏析】刘老师开门见山，清晰明了，同时充满童趣。重要的是，刘老师没有人为地“设计乘法口诀”，而是大胆地把学生的生成当成例题和素材，教学内容是学生即时生成的，这增加了教学的亲切感和可信度，使学生积极主动地参与数学学习，体现了“以生为本”的生态课堂。

（二）关于尾数。

师：下面研究第二个问题——“关于尾数”。大家都知道，任何一句乘法口诀都有得数，得数里就有尾数。你知道这个尾数是什么意思吗？

生：尾数的意思就是：比如最后那句七七四十九，结果49后面的9就是尾数。

生：那要是三三得九呢？

师：问得好！善于提出问题，特别是主动提出问题，是特别好的学习品质。

教师补充板书：3×3=9。

师：9的尾数是——

生：9是一位数，9就是尾数。

师：真不错！那我们一起说一说，这几句乘法口诀得数的尾数分别是几？（教师指板书）

生：32的尾数——2，81的尾数——1，24的尾数——4，49的尾数——9，9的尾数——9。

师：尾数嘛，就是“尾巴上的数”（有学生笑了），也就是个位上的数，对吧？下面我们研究第三个问题。

（三）关于对称。

师：第三个问题，“关于对称”。对称，学过吗？

生：学过。

师：轴对称图形，大家可能还记得，一个图形，如果把它对折以后能做到完全重合的话（教师双手做对折手势），那它就是轴对称图形。生活中对称的现象特别多，谁能举个例子？

生：蝴蝶的翅膀、花纹是对称的。

生：爱心也是对称的。

生：长方形和圆都是对称的。

师：没错，很多很多。同学们往黑板上看，刚才刘老师写了10个字的课题“乘法口诀尾数的对称性”，如果我们在中间画一条虚线当作对称轴的话（教师在“尾”和“数”中间画虚线）。我们看看两边，不看字的形状，只看位置，你看有没有对称的关系？你发现谁和谁对称？

生答略，效果如图1。

师：真好！大家看得很清楚。我再出几个数，看我这里。

教师在黑板上粘贴磁性数字卡片，如图2。

师：如果以5为对称轴，是不是两边也有对称关系？哪位同学能一个人把所有的对称关系都说出来？

生：1和9是对称的，2和8是对称的，3和7是对称的，4和6是对称的。

师：很好，很完整，也很有顺序。可是她怎么不说5和谁对称呀？

生：（纷纷地）5和自己是对称的。

师：你们说的也有道理吧。其实5正好在对称轴上，我们就再也找不到另外一个数和它相对应了，因此在这里没有和5相对称的数。

【赏析】学生之前学习的“对称”是图形的对称，其实对称也是一种关系。为了理解这种关系，刘老师利用文字之间和数字之间的位置关系引导学生展开想象，从而找到它们的对称性，既打破思维定式，发展了空间想象力，又感受到数学的美妙。

二、新授

（一）直观感受乘法口诀尾数相同时位置的对称性。

师：下面我们研究第四个问题“关于乘法口诀尾数的对称性”。

师：这是什么意思呢？我们举个例子，比如刚才有同学说了一句口诀：九九八十一，尾数是1，你觉得还有哪句乘法口诀的尾数也是1？

生：三七二十一。

生：还有一一得一。

教师板书：9×9=81，3×7=21，1×1=1。

师：（慎重地）还有吗？

生：（果断地）没有了。

师：能够很快做出否定的判断，也是需要勇气的。

师：尾数是1的口诀一共有3句，我们这样做，还是看“九九八十一”，我在数字卡片9的下面贴2个磁珠来表示2个9相乘，明白吗？

生：（点点头）嗯，明白。

师：谁到前面来帖“一一得一”？要是贴对了，请给他鼓鼓掌，表示赞同和鼓励。

一位学生在“1”下面摆了2个磁珠，其他学生热烈鼓掌。

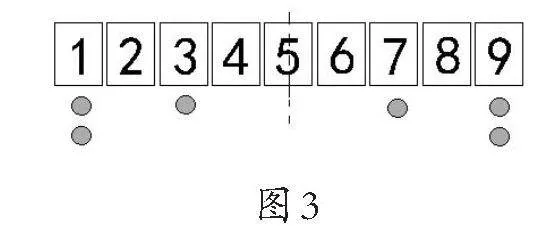
师：大家注意到了吗？这2个珠子（9下面的）和这2个珠子（1下面的），如果以5为对称轴的话，怎么样？

生：（兴奋地）是对称的。

师：对呀！居然是对称的，好玩吧？

生：（享受地）好玩！

另一个学生摆“三七二十一”，3下面摆1个珠子，7下面摆1个珠子。

师：鼓掌吧！大家看对称轴的左边和右边，想象一下，如果能够对折的话（做对折的动作），怎么样？

生：一样。

师：别说一样，应该说完全重合。

生：（齐）完全重合。

最后效果如图3所示。

师：好了。再看黑板，刚才还有同学说“四八三十二”，那么尾数是2的乘法口诀还有哪些呢？

学生找到尾数是2的乘法口诀一共有6句，教师一一板书。学生依次到前面来，把这6句口诀的因数贴到相对应的数字下面，如图4。

师：好了孩子们，对称吗？

生：（鼓掌）对称！

【赏析】“乘法口诀”和“对称性”分别属于不同年级、不同领域、不同单元。刘老师创造性地把貌似毫无关联的两个内容“交”在一起“相通”整合。通过“贴磁珠”，引导学生在做中学，直观感受乘法口诀中相同尾数的位置对称性，培养学生从不同角度思考问题。

（二）数形结合体会乘法口诀相同尾数形成的对称性。

师：下面我们进一步研究这个问题。尾数是1的口诀有3句，我们在乘法口诀表上把它们表示出来。当然，这个口诀表只有得数（如图5）。

师：来，观察一下，这是什么图形？

生：（齐）三角形。

师：不仅是一个简简单单的三角形，而且是——

生：（信心满满地）对称的三角形。

师：对，这个三角形有2条边相等，是轴对称图形。那么对称轴在哪里呢？

学生用手指在空中斜着画直线。

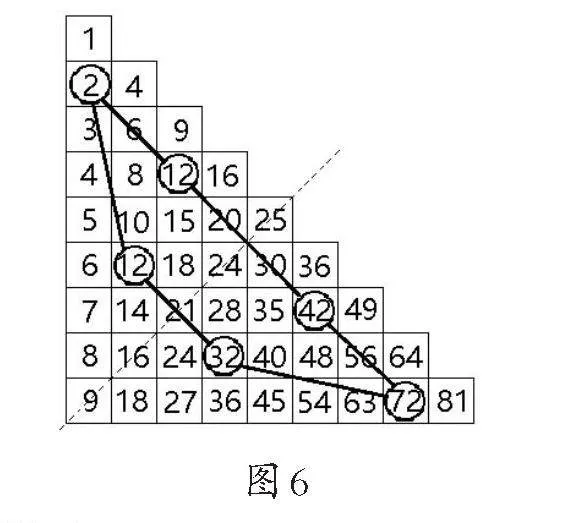
师：我们再看看尾数是2的口诀，一共有6句，我们依然按顺序把它们连接起来，得到的是什么图形（如图6）？

生：梯形。

师：（欣喜地）啊，你们还知道梯形啊！这个梯形也是轴对称的。我们再画出它的对称轴，像什么？

生：（惊喜地）像一把弓，还有箭。

生：对称轴是箭。

【赏析】通过研究尾数是1或2的乘法口诀各有几句，以及在乘法口诀表里找到尾数相同的得数并连接起来，刘老师引导学生在这个过程中体会到“数”与“点”的对应关系，在形成的图形中建立“数”与“形”的对应关系，渗透数形结合思想。伴随着直观图的呈现，学生不断经历着从“眼中有图”到“脑中有图”的过程，不断想象图形的形状，发展几何直观能力。

（三）探究乘法口诀尾数相同句数之和的对称性。

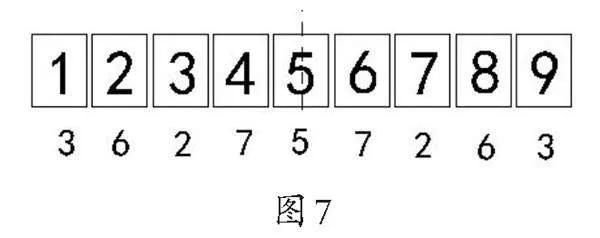
学生在老师的指导下，随机地把尾数是1～9的所有图形都在课件中展示了出来，而且各有多少句口诀也在黑板上书写出来（如图7）。

师：还有一个规律不知道你们发现没有。最左边3加6等于9。

生：右边6加3也等于9。

师：很好，接着说。

生：2加7等于9，7加2也等于9。

师：1个9，2个9，3个9，4个9，尾数是5的口诀只有5句，要是有9句就好了，正好就是45句口诀。好像丢了几句，我们在哪里丢了4句口诀？

大家都茫然了，面面相觑。

生：（忽然发现）丢了尾数是0的。

很多学生都表示赞同。

师：好，鼓掌祝贺！好多人往往只能看得到我们看得到的东西，看不到不容易看到的东西。满黑板都是我们能看到的，而这位同学却看到了黑板上没有的尾数是0的口诀，这种能发现数学问题的眼光就是非常有价值的能力。那么尾数是0的口诀有吗？

生：有，四五二十，二五一十，五六三十，五八四十。

生：（纷纷地）一共有4句。

就这样，老师继续带领学生在口诀表上，完成了尾数是1～9以及0的研究任务，画出来一个又一个轴对称图形，这里就不再赘述了。

不过有两个情况需要说明一下：

1.尾数是5的乘法口诀有5句，尾数是0的乘法口诀有4句，一共9句，它们可以在同一个等腰直角三角形上（如图8）。

2.尾数是3或7的乘法口诀都只有2句，在图上只能画出一条线段（如图9所示为尾数是3的情况），而线段也应被认为是轴对称图形。

主要板书如图10。

【赏析】当有学生发现丢掉了尾数是0的乘法口诀时，刘老师充满智慧的评语“好多人往往只能看得到我们看得到的东西，看不到不容易看到的东西”，鼓励学生逐步形成敢于质疑、深入思考的科学态度。

三、总结

师：刚才我们辛辛苦苦地研究了半天，刘老师忽然发现我们三（7）班的同学，包括我在内，好像都有点懵。

学生有些茫然。

师：你看，我们今天研究的这节课，数学书上没有，除了咱们三（7）班，其他三年级，甚至全国三年级小朋友都不学这个内容，而且考试也不考这些东西，你说我们学这干吗，有什么用？这就涉及我们今天研究的第五个问题。看屏幕，第五个问题是“关于本节课的意义”。这节课的价值在哪？意义是什么？为什么要上这节课？因为乘法口诀和轴对称图形看起来毫无关系，实际上是有联系的。知识间都是相通的。我写一写（准备板书）。同学们，我要写的是相通还是相同？

生：相通。

师：那相同是什么意思？

生：一样。

师：轴对称图形和乘法口诀一样吗？

生：不一样。

师：虽然不一样，不相同，但是它们是相通的。可以这样说，它们不同但是相通。这个“通”特别重要，而且在汉语里用“通”可以组很多词，谁来组词？

生：畅通，通过，通道，通关。

师：不错。刘老师也搜集了一些词语，用“通”组词较为重要的有——

课件出示，学生齐读：交通、沟通、贯通、普通、相通、通行、通话、通讯、通商、通航、通道、通过、通风、通读、通分、通顺、通畅、通透、通识、通达。

师：很好，我们这节是语文课吗？

生：不是，是数学课。

师：我们干吗要说这么多关于“通”的词语，是在做组词练习吗？

生：也不是。

师：那是为什么？

生：因为“通”很重要。

师：（十分肯定地）对极了！“通”很重要，很有意义。中国古代有一本书大家可能不太熟悉，叫作《易经》。

生：《易经》？

师：对。《易经》这本书很早，大约2000多年前，春秋时期，就是孔子生活的那个年代，是一部博大精深的古代哲学经典著作。《易经》里有这样一句话，可能对我们三（7）班同学很有帮助，大家请看——（出示课件，如图11）这是篆书，大家可能不太熟悉，现在大家写字经常用的是楷书，也叫楷体。试试看，能不能读出来。

生：（边笑边猜）天……地……

师：这种字体很难认，还是我来写吧。

教师板书：天地交而万物通。

师：来，读一遍。（生读）什么意思？谁能试着解释解释？

生：我觉得意思是天和地是相通的。

生：所有的东西都是相通的。

师：真好，鼓掌祝贺。古人认为天是最高的，地是最低的，那么在天地之间所有的万物都是相通的。其实数学知识之间是相通的，数学和语文之间、和体育之间、和外语之间，甚至和我们生活的方方面面之间都是相通的。万物都是相通的，用这种思想指导自己的学习，特别有帮助。

【赏析】乘法口诀尾数的对称性是教材中没有的内容，这是刘老师自己设计、自己执教的一节拓展课，也可以称为整合课。这节课的意义是什么？刘老师最后给出了答案：“相通”是这节课的灵魂。在刘老师的课中，我们可以看到：乘法口诀和对称性是相通的，数与形是相通的，数学学科与语文学科是相通的，数学与生活是相通的，数学与哲学是相通的……正如《易经》中所说：“天地交而万物通。”万物之间都是相通的，这是多么了不起的发现！

2022年版课标中强调对数学知识内容进行结构化整合，要关注知识的整体性、一致性和阶段性。其实也是在提醒我们教师教学时要注意联系，具有“天地交而万物通”的意识。只有这样，才能像刘老师一样，在数学教学中，上出以数学文化为底蕴，以培养数学思维为本质，以哲学为指导思想的有意义的好课。

刘老师三十年前就提出了“跳出数学教数学”的主张，其中涵盖“跳出教材教数学”“跳出教室教数学”“跳出教师教数学”“跳出学科教数学”等，把教学目标、教学内容、教学过程以及教学形式与生活实践相结合，与立德树人相结合，在更广阔的天地间开展教学活动，体现出生活中处处有数学、数学中也处处有生活的道理，这样的数学教育令人敬佩，也激励我们不断前行。

（作者单位：北京教育学院宣武分院，北京教育学院附属大兴实验小学）