让儿童在一致性视角下建构乘法的意义

乘法不仅与“数与代数”领域的整数、分数、小数、比例等概念和相关运算定律有关，而且与“图形与几何”领域的周长、面积、体积等概念和计算公式也有密切联系。建构乘法意义、形成乘法模型，可以让儿童更好地掌握小学阶段的基本数学概念、法则和原理。但在实际教学中的情况如何呢？

【一道题引发的思考】

这是一道二年级上学期的期末试题（如图1），主要测评学生“在具体情境中理解乘法运算的意义”的水平，通过对G区地处城市、农村的三个班级共162份样卷的分析，大致可以分为图中的4种典型作答情况。学生对于“乘法意义”的不同理解水平引发我们的深入思考。

思考一：儿童为什么会用数数的方法求总数？

为什么经过一学期23个课时关于“乘法意义及其运算”的专项学习后，当学生遇到一个“零散的实物堆”情境图时，还是用数数的方法求总数呢？张奠宙教授明确指出：自然数的加法说白了就是数数。A、B两堆石子，先数A堆的a颗，接着数B堆的b颗，最后的结果就是（a＋b）颗。当代数学教育心理学的一个经典结果就是用数数这样一种行为性的操作活动来形成自然数的概念。加法概念不是来自更多的小石子，而是来自添加或合并的操作活动。

思考二：如何让儿童理解乘法、加法运算和数数的一致性？

乘法运算可以追溯到加法，而加法运算可以追溯到数数。这样，就保持了运算的一致性。数数是学习乘法意义的起点，要让儿童经历数数的过程，认识到乘法与加法是同构的。因此，“乘法的初步认识”的教学可以从数数活动引入，引导学生感受加法与数数的一致性；接着在解决“多个相同数连加问题”的过程中，引导学生初步理解乘法是同数（整数）相加的简便运算。

【“乘法的初步认识”重安排】

一、激活数数经验，感受加法与数数的一致性

数数是儿童最早的也是最普遍的关于数学学习的活动经验。如果只是从教材主题图中的3道加法算式引出乘法，那么，既不能加深儿童对乘法与加法之间联系的认识，也不能有效地激发其“求简”的愿望。因此，我们精心创设了丰富的数数活动，引导儿童列举更多的、更长的同数相加的算式，在顺承数数经验的同时，乘法的意义呼之欲出。

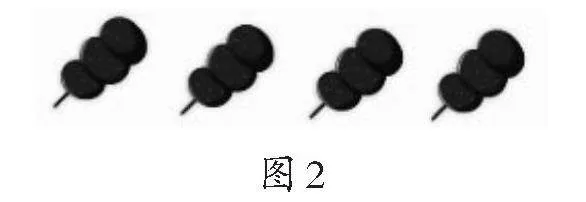
1.用课件出示图2：

师：一共有多少个山楂？

生：1、2、3、4、5、6、7、8、9、10、11、12。

师：1个1个地数，数了12次，一共有12个山楂。还可以怎么数？

生：还可以3个3个地数，3、6、9、12。

师：你能根据自己的数法列出算式吗？

生：3＋3＋3＋3=12（个）。

2.用课件出示图3：

师：黄瓜又有多少根呢？

生：可以5个5个地数，5、10、15，算式是5＋5＋5=15（根）。

师：真好，这比1个1个地数数更加简便了。

师：大家认真观察一下，这两个加法算式有什么相同点？

生1：加数都相同。

生2：第1题是4个3相加，第2题是3个5相加。

师：生活中也有这样用相同数连加来解决的问题吗？

生：1只蚂蚁有6条腿，3只蚂蚁一共有6＋6＋6=18（条）腿。

生：在学校吃午餐时，每人发2个小蜜橘，全班就要发2＋2＋2＋……一口气说不完了。

生：这样写太麻烦了，有简单些的写法吗？

二、再编绘本情境，发现乘法与加法的一致性

乘法的意义是不断丰富、发展起来的，弗赖登塔尔、格里尔等都对乘法的现实模型进行研究，总体而言，乘法主要包括等组模型、倍数模型、矩形模型和笛卡儿积模型等。以上四种模型中，最基本的是第一种模型，其他几种模型都可以转化为第一种模型，但其缺点是只能写出一个加法算式。而矩形模型不仅直观，而且可以多元表示，写出两个不同的加法算式。为了帮助儿童深入理解一个加法算式可以写出两个乘法算式，一个乘法算式对应两个加法算式，我们精心再编了《幸运农夫的三个宝贝》的绘本情境，拾级而上地使用等组模型和矩形模型，让低年级儿童在“善”的故事、“美”的画面中，真正理解“乘法是加法的简便运算”的内涵。

1.女儿剥的花生——在等组模型中发现特殊加法的简便。

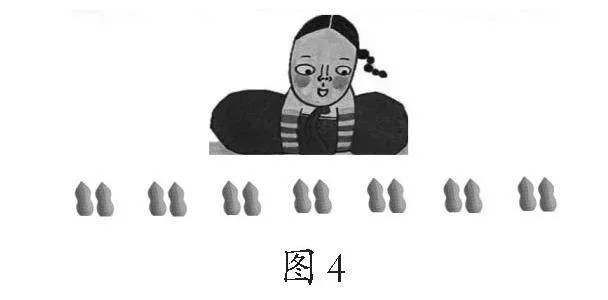
师：大家在生活中遇到过相同数连加的情况，国外的小朋友也有相似的经历。在一个僻静的村子里，住着一个勤劳的农夫。有一天，他在地里劳动时发现了一个五彩袋，于是赶紧回家送给了宝贝女儿。女儿把正在剥的2颗花生放进了五彩袋，神奇的事情发生了……（如图4）

师：一共有多少颗花生？你是怎么知道的？

生：2＋2＋2＋2＋2＋2＋2=14（颗）。

生：我可以列出7×2=14（颗）来计算。

师：出现乘法算式了，同学们有什么不明白的问题，可以大胆地提出来。

生：“×”是什么意思？

生：7是怎么来的？2表示什么意思？

生：7×2又表示什么呢？

师：大家提的问题很有价值，我们一起来认真观察。

课件出示图5：

师：你们有什么发现吗？

生：这3道题里的加数都相同。

师：对，我们刚才数山楂的总个数时，每次数3，数了4次；数黄瓜的总根数时，每次数5，数了3次；数花生的总颗数时，每次数2，数了7次。像这样把几个相同数加起来就可以用乘法表示。

教师结合课件的动态演示，介绍乘号的来源。（如图6）

师：这样，我们在求花生的总颗数时，除了可以用2＋2＋2＋2＋2＋2＋2=14来计算，还可以写成乘法算式：2×7=14或7×2=14。现在你知道2表示什么，7又表示什么了吗？

生：2表示每次数2个，7表示数了7次。由此我还解决了一个新问题，上一周我会背诵《春江花月夜》了，大家知道吗，这首七言长诗一共有36句，252个字。要是用以前的加法算式来表示，恐怕要写上两三行，但今天学过乘法后，就可以简简单单列式为36×7=252，或者7×36=252，太方便了！

2.妈妈喜欢的花——在矩形模型中阐发乘法的意义。

师：农夫的妻子看见五彩袋也很好奇，就把自己最喜欢的花放进去，不一会儿，五彩袋就变得鼓鼓囊囊，一朵又一朵的花飞出来，她认真地数了数花的总数，正好可以用乘法算式5×3来表示。大家能用自己的学具摆一摆吗？

学生操作后，呈现不同的摆法：（如图7）

师：看来大家摆的小花图有些不同，哪些方法是正确的呢？

生：第一种是正确的，因为每次数5朵，这样数3次，就是有3个5相加，可以列成乘法算式5×3。

生：第二种也对，因为每堆摆3朵花，摆5堆，就可以表示5×3。

生：第三种比较特殊，横着看是3个5，竖着看是5个3，都可以用乘法算式5×3来表示。

师：明白了，原来一个乘法算式可以表示两种意义，最后一种摆法对吗？

生：不对，他虽然也用到了5和3，但是她摆的是5＋3，是把5和3直接合起来，而不是3个5相加。

师：如果五彩袋又变出了3×10朵花，一共会是多少朵呢？

生：10个3相加不好算，但3个10加起来就简单得多，我们可以用10＋10＋10=30。

生：我发现了，虽然两个加法算式改写成的乘法算式写法一样，但由于乘数表示的意思不一样，所以一个表示的是10个3相加，另一个表示的是3个10相加。

生：是的，“10个3相加”和“3个10相加”都可以写成10×3或3×10。但只要是表示“10个3相加”的含义，就是指每次数3，数了10次；而“3个10相加”就是指每次数10，数了3次。

三、解决实际问题，领悟运算与数数的一致性

儿童从数数的经验、加法的经验出发，在计算多个相同数相加时产生求简的朴素愿望，他们通过“多个数相加”“换一种算式表示相加”“同一个算式表示的意义不同”的探索过程，初步理解了“乘法是加法的简便运算”的内涵，将乘法纳入了“特殊加法”的运算结构。但这还不是“乘法的初步认识”的终点，我们要让乘法回到真实且复杂的生活情境中去，使学生领悟乘法和加法运算与数数的一致性，以促进他们在将来学习除法运算时，发现除法也依然是数数活动，只是除法与乘法有“倒着数”“正着数”的区别。为了促进儿童深刻领悟乘法和加法运算与数数的一致性，认识到运算是“快速地数数”，而乘法相对于加法来说“数得更快”，我们精心设计真实且复杂的生活情境，着力打造低门槛、多层次、大空间的“看图列乘法算式”（如图8）。即第1题是乘法意义的巩固；第2题是“解决问题”的雏形，4是显性的，2是隐性的；第3题通过圈一圈自主确定加数，可以是1、2、3、4、6中的任意一种；第4题是“创造乘法”，将2本书移到4本书上，变出相同加数“6”。

【本文系河南省教育科学“十三五”规划2017年度一般课题“指向儿童数学核心素养发展的问题情境创设的研究与实践”（编号：2017—JKGHYB—0485）的研究成果之一】

（作者单位：河南郑州市管城回族区教体局教师发展研究中心）