基于数字散斑相关的土体剪切带自动识别方法与应用

徐晓华 ，李元海 ，朱鸿鹄，王迎超

(1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221116；2. 中国矿业大学 力学与土木工程学院，江苏 徐州，221116；3. 南京大学 地球科学与工程学院，江苏 南京，210023)

剪切带的萌生、发展和贯通是岩土体灾变过程中应变局部化的宏观表现，是多数岩土体变形破坏的征兆和前提，如边坡土体的滑动破坏，室内土工试验土样的剪切破坏等，自20世纪80年代以来，一直受到固体力学、材料科学、岩土力学等领域科技人员的密切关注[1-3]。

目前，在土体剪切带的形成机理、识别和变形分析等方面，研究者展开了许多细致的研究，并取得了丰富的成果，但在模型试验中，土体剪切带的自动识别方法与应用方面还需要进一步研究。在岩土模型试验中，土体剪切带的分析研究主要依靠内部观测和表面观测2种方法。内部观测有X 射线、CT 扫描以及光纤传感等技术。X 射线技术可以用于分析土样在剪切过程中的微观力学行为，但该方法所使用的测试设备昂贵，试验操作复杂，剪切带的形状识别也比较粗糙[4]。CT 扫描技术可以通过扫描得到3D图像来定量分析剪切带的扩展演化过程，但设备昂贵[5-6]；利用埋入式的应变传感光纤，可以推算土体剪切变形量，但分析结果受到纤土耦合性的影响，需要借助于较为繁琐的标定工作来提高精度[7-8]。

土体剪切带的表面观测方法主要有描画网格法和数字照相法。ALSHIBLI 等[9-10]采用描画网格法分析剪切带形成的过程，通过在薄膜上描绘网格，比较摄像机采集的试验图像，测量剪切带取向角和厚度，但该方法对操作要求高，且识别精度较低。与之相比，数字照相技术克服了接触式变形量测的不足，操作简单且成本低。李元海等[11]提出了一种基于DSCM 的土体剪切带识别与量测方法，并应用于一个大型砂土剪切试验，其结果表明了该方法的可行性。金爱兵等[12]采用数字图像相关(digital image correlation, DIC)技术开展了矿岩散体直剪试验，研究了剪切作用下矿岩散体颗粒剪切面颗粒运动、局部应变和剪切带的演变规律。王学滨等[13]提出了改善剪切带边界附近位移测量精度的环绕测点子区分割一阶DIC方法，通过对虚拟剪切带位移进行测量以及与基于粒子群优化和Newton-Raphson迭代的粗-细方法结果进行了对比，验证了该方法的有效性。上述基于数字照相的土体剪切带测量都是在得到高清图像的前提下，利用相关图像分析软件进行识别，其过程需要辅助大量的人工处理，尚未实现土体剪切带的自动、准确识别。

李元海等[11,14-15]自主研发的数字散斑相关分析软件PhotoInfor可以有效分析模型试验图像的剪切带的演变过程，但其分析过程中仍需人工辅助处理。为此，本文作者对其进行二次开发，提出并实现了土体剪切带的自动识别，以减少人工识别的误差，对土体剪切带形状准确识别和变形精细分析具有重要意义。

1 剪切带数字散斑相关分析方法

1.1 数字散斑相关方法

数字散斑相关方法的基本原理是：对于利用数字图像设备连续采集的含位移的数字散斑图像，在首张图像中设置量测像素点(这里称之为“测点”)，以测点为中心，构建一个固定大小的像素区域(又称“子区”[16])，通过图像相关性搜索的方法计算与相邻图像上指定搜索区域内所有测点子区像素点灰度的相关系数，并将最大相关性系数对应的测点作为搜索目标点，以此实现序列图像上设定测点位置的连续追踪，然后，根据图像间对应测点的坐标变化进行微小位移计算，通过连续累加获得测点的最终位移，从而实现观测目标数字散斑图像上测点的位移测量。

本文采用的PhotoInfor软件是一款自行研制的高精度岩土变形量测软件系统[17-18]，相对于国内外同类软件，PhotoInfor 针对岩土材料非连续与局部化两大变形特点进行了专门处理。软件采用稳定的相关性计算公式进行图像分析和位移计算，应用有限元四边形等参单元变换的方法实现图像校准和应变计算。同时，为适应砂土模型复杂的变形特点，采用平移和旋转搜索方法进行位移追踪，可满足土体剪切带识别、分析的精度要求。

1.2 土体剪切带分析流程

利用PhotoInfor软件对试验中采集的图像进行剪切带分析，主要包括剪切带形状和边界点的自动识别、变形分析和厚度计算，具体分析流程见图1。其中，图像采集分辨率越高、测线布置越密集都可以有效提高剪切带的识别精度，但会大大增加计算量，因此，在实际操作过程中，应根据实际需求进行调整。由于本文研究的主要内容在土体剪切带形状、边界点自动识别以及剪切带的变形分析和厚度计算，有关流程的详细介绍可参见文献[14]。

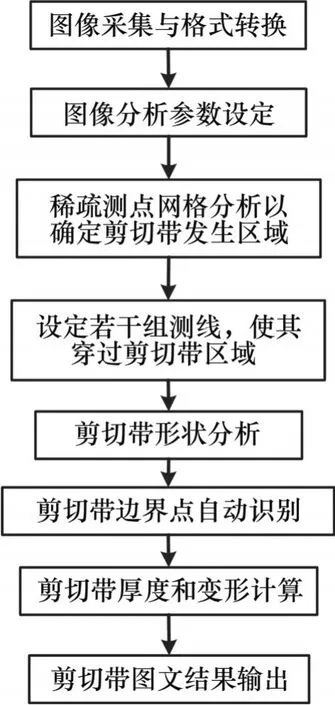
图1 剪切带分析流程Fig. 1 Shear band analysis process

2 砂土剪切带自动识别与变形计算方法

2.1 剪切带形状识别

由于颗粒大小和颜色各不相同，砂土图像呈现为明显的散斑状，无需手动绘制散斑场。因此，本文基于砂土直剪试验采集的连续剪切变形图像，采用PhotoInfor 进行剪切带形状分析，其过程如下。

1) 剪切带范围圈定。考虑到多测点图像分析计算量大且耗时长，并且在剪切带范围不明的条件下，布置较少的测点不利于剪切带的识别，布置较多的测点又会增加图像分析的时间和计算量，可以通过稀疏网格测点进行初步粗略分析，找到剪切带的分布区域，缩小剪切带测线的布置范围，如图2所示。

2) 剪切带正式分析。在已知剪切带分布范围的基础上，布置垂直穿越剪切带的多条测线，每条测线由连续排列的测点组成，各测点之间相距1像素。通过测点的连续追踪，计算测线上各测点的位移，获得多组测线的“弯折”形态来实现剪切带形状的自动识别。方法原理如图3 所示，其中，图3(b)中的褐色填充区域为分析得到的剪切带区域，将相邻4个边界点首尾相连构成的封闭四边形称为测点单元。

剪切带分析结束后，需要找到剪切带边界点来构造测点单元以便分析变形和计算厚度，目前在边界点识别方面主要依赖人眼识别和人工选取，效率低且受主观性影响大，并且由于边界点附近测点较为密集，难以依靠人眼选出边界点。因此，本文对PhotoInfor软件中的剪切带识别功能进行完善，以实现土体剪切带边界点的自动识别功能。

2.2 剪切带边界点自动识别方法

针对上述砂土剪切带分析中测线会在边界点点处产生明显“弯折”的特征，基于测点的坐标，提出一种基于最小二乘法拟合与曲率最大值判断的剪切带边界点自动识别方法，具体算法如下。

1) 亚像素线性插值。依据单条测线的坐标可绘制其对应的测点分布图，如图4所示。从图4可以看出，剪切带两侧的测点分布较为密集，而剪切带内部测点较为稀疏，其主要原因是剪切带内部位移变化较大，使得测点之间的间距也变大，测点数目变少。

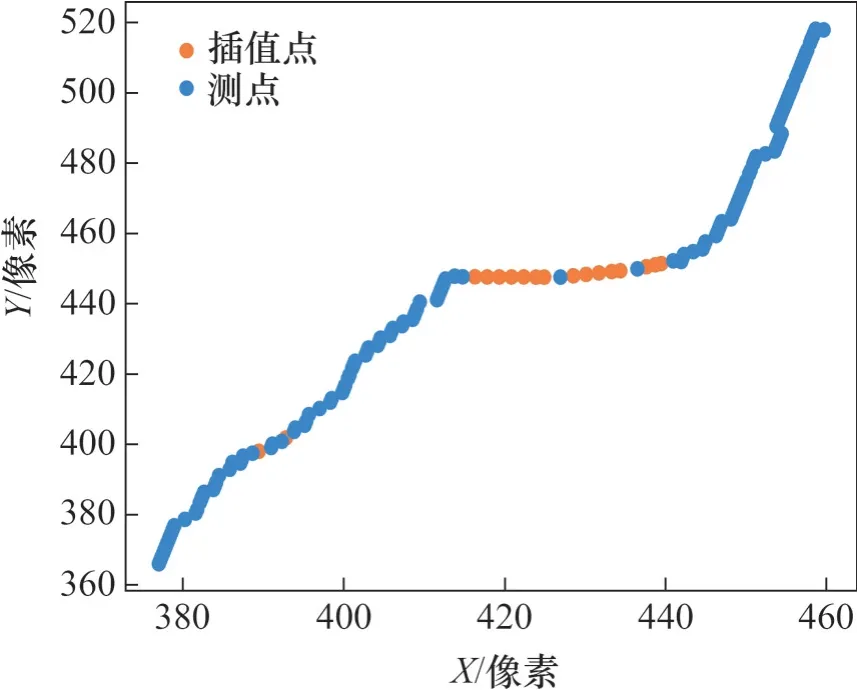
图4 单条测线变形后测点分布Fig. 4 Distribution of measuring points after deformation of a single measuring line

为了保证拟合曲线尽可能贴合测点分布，防止曲线有过大起伏，需要在距离过大的测点间进行插值。考虑到本文测线绘制时测点的布置间隔设置为1像素，可以近似认为任意两测点间的亚像素点变形是相同的。因此，本文采取线性的方式对测点间距高于一定阈值的部分进行插值处理(图4)。

2) 拟合曲线。针对离散测点，采用多项式拟合方程和最小二乘法拟合数据。在实际拟合中发现，当多项式最高项次数过小时，拟合效果较差，无法达到预期要求；而当多项式次数过高时，又会造成过拟合，曲线弯折点较多。因此，最终将多项式最高项次数确定为8次。拟合线方程为

式中：i为幂指数，最小取值为0，最大取值为8；ai为第i项系数。测点拟合曲线见图5。

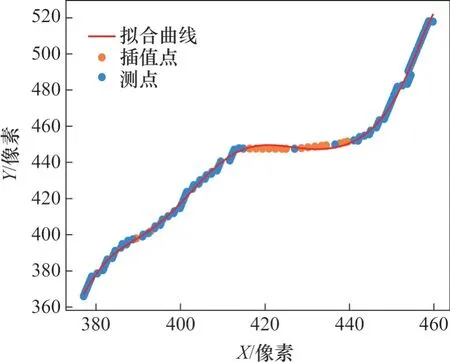
图5 测点拟合曲线Fig. 5 Schematic diagram of measuring point fitting curve

3) 边界点识别。剪切带边界点通常为土体由应变缓慢增加到急剧增大的转折点，在拟合曲线上则表现为弯曲程度最大的2 个点。依据这种思想，本文采用曲率作为弯曲程度的衡量指标，通过式(2)计算曲线上各点的曲率K(x)，找到其中最大的2个极值点即为最大弯曲点。

式中：F′(x)和F″(x)分别为拟合曲线一阶与二阶导数，

图6所示为各点曲率的分布图。从图6可以看出，有2个明显较大的极值点，对应曲线的最大弯折点；此外，还有其他较小的极值点，这主要是因为剪切带外的部分测点分布不均匀，拟合时形成了较小的弯折，对识别效果影响较小。

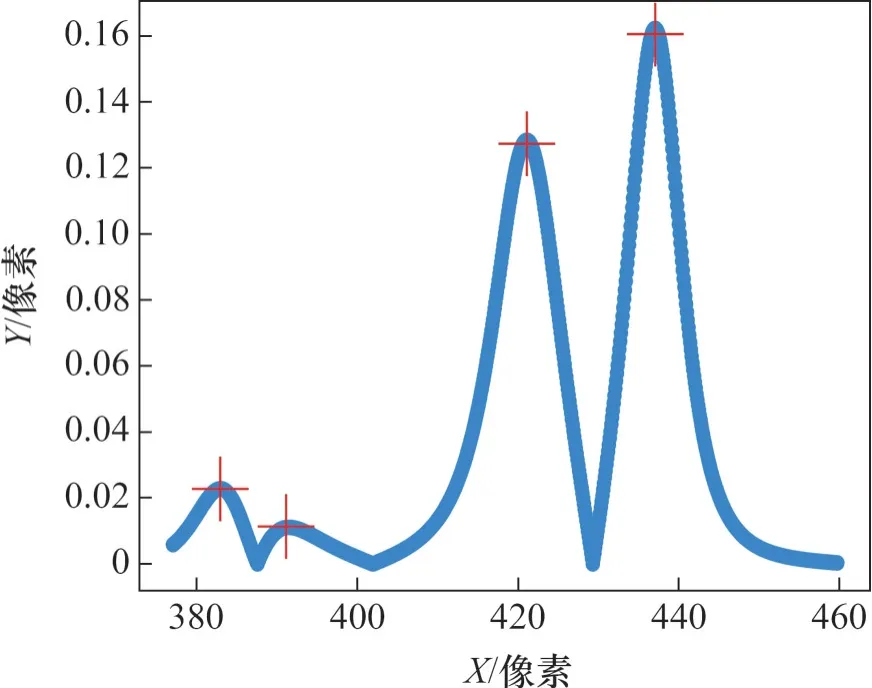
图6 拟合曲线的曲率分布图Fig. 6 Curvature variation of fitting curve

实际上，曲率最大点并不是剪切带测线上的边界点，而是离边界点最近的拟合曲线上的点。因此，需要进一步计算各测点到曲率最大点的距离，距离最小的测点为实际边界点。图7所示为某条测线穿越的剪切带边界点最终识别结果。

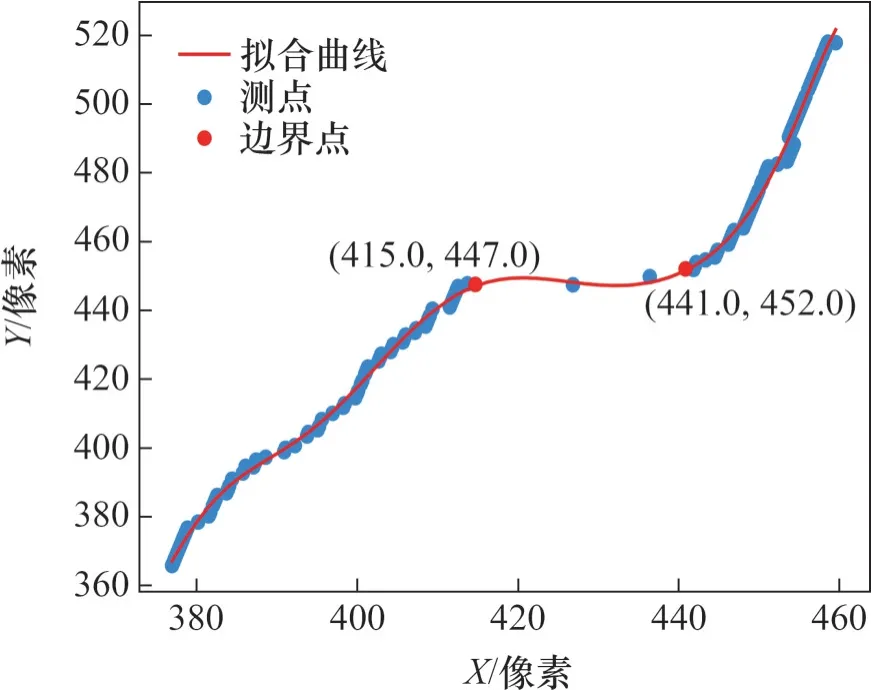
图7 剪切带边界点识别结果Fig. 7 Identification result of shear band boundary point

2.3 不同倾角下剪切带边界点的识别

在实际剪切试验中，剪切带可能会形成不同的倾角，其测点分布也会呈现不同的形状，影响曲线的拟合效果。为此，本文通过测点旋转的方法模拟不同倾角下剪切带测点分布，开展曲线拟合研究，并引入拟合优度R2对拟合效果进行定量评价。R2的取值范围为[-∞， 1)，其越接近1，则拟合效果越好。式(3)和式(4)分别为测点逆时针旋转的坐标变换公式和R2计算公式。

式中：(X′i，Y′i)为旋转后测点坐标；(Xi，Yi)为初始测点坐标；(XS，YS)为基准点坐标；θ为逆时针旋转的角度；yi为拟合值；Yi测点坐标，-Y为测点平均坐标，n为测点个数。

图8所示为通过旋转前后不同倾角下的测点的拟合效果。从图8可以看出，对于旋转前测点分布图，剪切带倾角较大，拟合曲线的R2偏差值较大，测点拟合效果极差，无法继续搜索边界点；对于旋转后测点分布图，剪切带倾角较小，拟合曲线的R2接近于1，曲线拟合效果较好。因此，亟需研究一种适用于不同倾角的边界点识别算法。

图8 旋转前后测点的拟合效果Fig. 8 Fitting effect of measuring points before and after rotation

针对上述问题，本文提出一种最优拟合线搜索的边界点识别算法，即通过测点旋转与拟合效果评定来确定拟合线，继而求得边界点坐标。具体算法如下。

1) 旋转范围的确定。为了保证搜索范围能够包含所有的倾角，本文选择-90°～90°作为旋转范围，考虑到旋转角度的间隔相差较小时对拟合曲线影响不大，且会增加计算时间，因此，将旋转间隔确定为0.5°。

2) 测点旋转与拟合。以第一个测点为基准点，依次在-90°～90°范围内每隔0.5°对测点分布图执行旋转操作，然后按照上述所示的方法对旋转后的测点进行插值与曲线拟合并计算相应的R2。

3) 边界点识别。找出R2最大时的旋转角度β，将该角度下的拟合曲线确定为最佳拟合线，并对此曲线执行边界点识别。图9所示为R2最大时的边界识别图，可见：边界识别曲线拟合效果与识别结果都符合预期。最终将识别到的边界点绕基准点顺时针旋转β即可得到实际边界点。

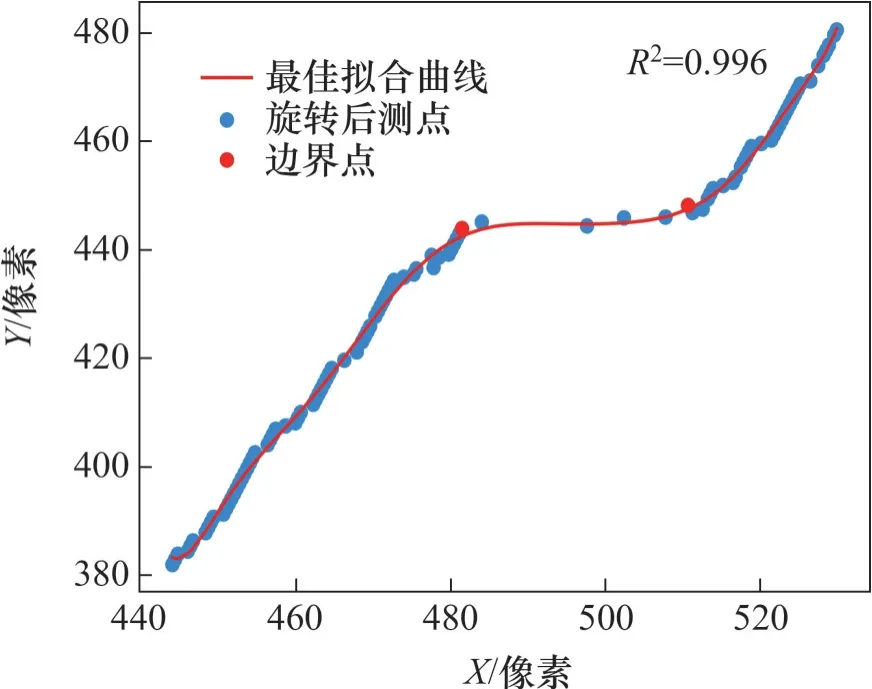
图9 最优拟合线下的边界点识别结果Fig. 9 Recognition results of boundary points under the optimal fitting line

2.4 剪切带厚度计算方法

目前剪切带的厚度测量主要有理论推导和试验测量2种方法。本文在自动求得边界点坐标的基础上，提出一种求解剪切带厚度的简单方法。首先，将相邻4 个边界点相连构成1 个四边形单元，并将量测线上边界点(下边界点)相连的直线作为该等参单元的上边界线(下边界线)；然后，根据边界点的坐标，计算得到每个边界点到非所在剪切带边界线的距离，最终求取这4个距离平均值作为剪切带的厚度。图10 所示为剪切带厚度计算原理的示意图。图10 中，A、B、C、D为相邻两条测线上的4个边界点，分别求出A、B点到线段CD的距离和C、D点到线段AB的距离，以D点到线段AB距离D4的求解为例，假设A、B、D点的坐标分别为(xA，yA)、(xB，yB)、(xD，yD)，通过式(5)求得线段AB、BD和AD的长度LAB、LBD和LAD，则D4可由式(6)计算得到。

图10 剪切带厚度计算原理Fig. 10 Principle of shear band thickness calculation

同理，可求得A点和B点到线段CD的距离D1和D2以及C点到线段AB的距离D3，最终剪切带的厚度可表示为

2.5 剪切带变形计算方法

测点的位移可以通过不同图像上对应点坐标的变化直接求得。借用有限元中常用的四边形等参单元的概念与方法，可以实现测点应变的计算[17]。在自动识别得到剪切带边界点坐标后，以4个边界点为角点的矩形可看作1个四边形单元，在4个角点的坐标和位移已知的情况下，通过图11所示的坐标变换可进行中心点的位移计算，计算公式如式(8)所示。

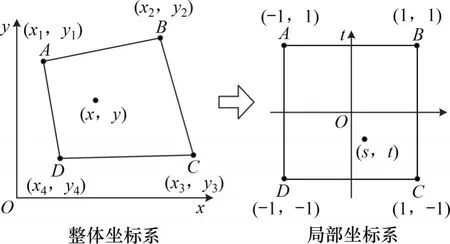
图11 基于四边形等参单元的坐标变换Fig. 11 Coordinate transformation based on quadrilateral isoparametric element

式中，(si，ti)为局部坐标系下第i个顶点的坐标；i=1，2，3，4；(s，t)为点(x，y)对应的局部坐标；(ui，vi)为第i个角点在x和y方向上的位移分量。

由式(9)可求出四边形中任意一点(x，y)的正应变εx、εy以及剪应变γxy和体积应变εv。

式中：(X，Y)为变换后的坐标。

3 应用试验

3.1 试验概况

采用自行设计的剪切试验装置，试验模型长×宽×高分别为300 mm×200 mm×40 mm，采用日本标准豊浦砂，应用空中下落法制作而成，砂漏出口在剪切盒上方约1 m处，以剪切盒竖向中心线为准，砂漏左右移动范围各为30 cm，移动速度为30 cm/s，移动6～7次将砂土填满剪切盒。具体试验过程见文献[11]。制作的模型相对密度可以达到85%以上，平均密度为1.60 g/cm3。水平剪切前后土体变化如图12 所示，图中，FV为垂直荷载，FT为水平荷载。经过剪切后，土体上下部分发生错动。

图12 砂土剪切试验示意图Fig. 12 Schematic diagrams of sand shear test

3.2 剪切带识别

图13(a)和(b)分别为试验图像在剪切带分析前后的测线布置情况。由图13(a)和(b)可以看出：砂土中间部分出现明显的应变局部化现象，即剪切带形成与发展区域。由自动分析得到的边界点位置可见剪切带在测线3 出现了明显下降。图13(c)所示为剪切带边界点自动识别效果和绘制的测点单元，可见，在剪切带分析完成后，通过二次开发的自动识别功能，可自动计算并将边界点位置与序号标在原图上，将这些边界点按顺序依次相连，得到的带状区域即为剪切带的形状。

图13 剪切带分析与四边形等参单元标识Fig. 13 Shear band analysis and drawing of quadrilateral isoparametric element

总体来看，识别程序可以较好地识别出剪切带的边界点和形状。将相邻的4 个边界点依次相连，可以得到图13(c)所示的5 个测点单元，分析这些测点单元可得到剪切带不同位置的位移变化和剪切带厚度。

3.3 边界点识别结果对比

为了验证边界点自动识别的准确性，分别对边界点采用人工选取和自动识别2种方法进行对比验证，对比结果如表1所示，其中，ID号与测点一一对应，人工选取结果与自动检测结果越接近表示识别效果越好。

表1 边界点识别结果(测点ID号)对比Table 1 Comparison between results of two boundary point identification methods

由表1 可得，人工识别与自动识别的测点ID号基本一致，仅在上边界点2和上边界点5处略有差异，其主要原因是这两处测点较为密集，判断难度大。自动识别能够提高识别效率，且能够有效避免人工识别的误差。

3.4 剪切带变形分析

识别出剪切带边界点后，每相邻4个边界点可构成1 个四边形单元。除了具有识别边界点功能外，PhotoInfor 还有变形自动计算功能，通过分析剪切带得到了正应变、最大剪应变γmax和体积应变随剪切位移的变化规律，如图14所示。

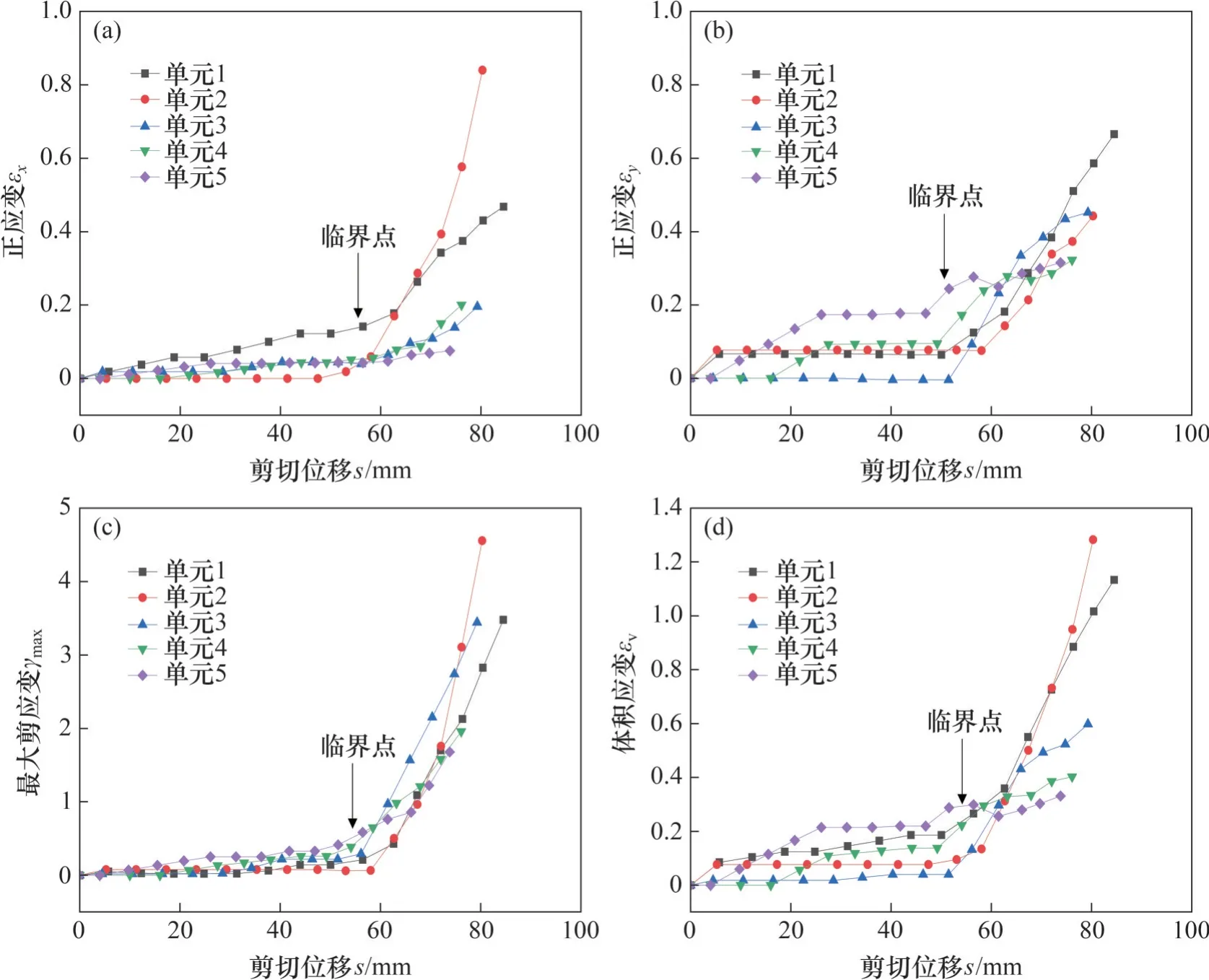
图14 剪切带不同位置处应变-剪切位移关系曲线Fig. 14 Strain and shear displacement relation curve at different positions of shear band

从图14(a)和(b)可以看出：在砂土剪切过程中，x和y方向上正应变的变化过程相似，当剪切位移s在临界点前(s=55～60 mm)，正应变保持为零或缓慢增加，此阶段剪切带变形相对缓慢；当s超过临界值时，正应变急速增长，此阶段剪切带变形急剧增加。需要注意的是，单元5的y方向正应变在剪切位移较小时(s=4 mm)突然增加，然后保持稳定，又在s=55 mm时开始激增。其主要原因是：图13 中测线6 边界点上方部分土体较早时产生了局部滑移，其边界点位置也相应地发生了变化。从图14(c)和(d)可以看出：最大剪应变在临界点前时接近于0，而在临界点后最大剪应变开始急速上升，与正应变变化过程相似；体积应变也在临界点前增长缓慢，而在临界点后激增。由于剪切带变形先后经历了缓慢增长和急速增长2个阶段，并且各个单元的体积应变均大于0，剪切带内土体都具有为体积膨胀的特点。

综上分析可以看出：剪切带内有2 个变形特征，一个是剪切带变形可分为缓慢增长和急速增长2个阶段；另一个是在剪切过程中，剪切带内的土体始终呈现剪胀的特点。

3.5 剪切带厚度分析

在识别出剪切带边界点后，PhotoInfor 软件可根据各等参单元自动生成剪切带不同位置处的厚度。表2所示为等参单元1～5中心点处的剪切带最终厚度测量结果。由表2可以看出，剪切带不同部位处的厚度有所差异，除单元2外，其余的剪切带厚度都在3 mm以上，且差别较小；但在单元2处，剪切带厚度为1.27 mm，与其他部分相比差异较大，主要原因是在图13 中测线3 处剪切带明显下降，使得等参单元2较为扁平。最终得到除去单元2厚度后的剪切带平均厚度为3.50 mm。

表2 剪切带厚度测量结果Table 2 Results of shear band thicknessmm

4 结论

1) 基于数字散斑相关原理，提出了一种基于最小二乘法曲线拟合与曲率判断的土体剪切带自动识别新方法。针对不同倾角下剪切带边界点识别问题，设计了一种最佳拟合线搜索算法，并将其集成到自行研制的软件系统PhotoInfor中。

2) 基于土体剪切带边界点坐标识别结果，进一步给出了一种土体剪切带厚度的简明计算方法，并分析了砂土在大型直剪试验中剪切带的厚度及其空间分布特点。

3) 在土体剪切带自动识别基础上，利用PhotoInfor 分析获得了砂土在大型直剪中剪切带内应变的演化特征，发现剪切带变形可分为缓慢增长和急速增加2个典型阶段，剪切带内土体变形始终呈现剪胀特征。

4) 人工手动所得结果和程序自动识别的结果基本一致，但程序自动识别的效率显然更高，且能够减少人工识别的人为误差。