基于改进迭代求解的双孔洞围岩应力场解析研究

蔡鑫，陈立业，周子龙，谭力海，阳俊

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；2. 南华大学 资源环境与安全工程学院，湖南 衡阳，421000；3. 湖南有色金属职业技术学院 资源环境系，湖南 株洲，412000)

地下工程中常包含不同形态的孔洞，如硐室、隧(巷)道、溶洞以及采空区等。由于孔洞周围的应力集中引起岩体变形与裂纹萌生扩展，极易诱发岩体整体失稳[1-3]。在地下工程中，局部区域内往往存在多个孔洞，这些地下孔洞几何形态与空间分布特征各异，当孔洞间距较小时，彼此会相互影响，致使其周围应力场分布特征十分复杂[4-5]。为揭示外荷载作用下多孔洞围岩系统的损伤破裂特征及机制，国内外学者进行了大量研究，如YANG 等[6-9]开展了外荷载作用下圆形、椭圆、矩形双孔洞的室内试验与数值仿真研究，获得了不同形状孔洞的方位角及相对位置对岩石力学性质及裂纹演化的影响规律。然而，以上研究局限于孔洞对岩石试样力学性质与破坏模式的影响，对相邻孔洞相互作用机理研究较少，更缺乏对孔洞体系周边围岩应力分布的定量分析。实际上，相较于室内实验和数值模拟，应力解析方法可靠性高，能对地下孔洞相关的工程问题进行快捷计算，并对相关设计参数进行分析，可为地下工程设计与施工提供重要参考，具有重要的理论意义与应用价值。在含孔洞围岩应力分析研究中，对非圆类复杂几何形状，常用复变函数方法求解以获得高精度的解析解[10-14]。目前，对单个孔洞问题的复变函数解析理论较完善[14-17]，但对于2个或多个孔洞的情况，由于邻近孔洞之间的相互影响，此时围岩的应力分布与单个孔洞情况存在显著区别，其应力函数也变得更加复杂。为此，JEFFERY[18]采用双极坐标法研究了含双圆孔无限域的应力场，并给出了双坐标下双调和应力函数的一般形式。在此基础上，LING[19]对含双圆孔无限域的应力场进行了研究。KOOI等[20]对深埋双平行巷道的应力场进行了计算。MINDLIN[21]对孔洞应力场进行了初始化处理，并推导了考虑重力场的应力函数。朱大勇等[22-23]基于应力叠加原理，将含多个孔洞的无限域中应力场当作各个单独孔洞在洞口内边界上作用虚拟面力产生的应力场的叠加。此外，Schwarz交替法也是解决含多孔洞的多连通域问题的一个重要方法。早期受限于当时的计算条件，只能完成1 次迭代，其求解精度较低[24]。近年来，随着计算机计算能力提升，张路青等[25]利用Schwarz 交替法对双圆形孔洞体系区域应力场求解，通过2次迭代，显著提高了求解精度。

基于迭代求解双孔洞体系应力场的核心问题是通过求解每步迭代过程中的应力解析函数得到在孔洞边界产生的多余面力，而这涉及复变应力解析函数或孔洞边界坐标点在不同坐标系的转换问题。对于圆形孔洞，其映射函数和逆映射函数表达式简单，可直接对应力解析函数进行上述转换。而对非圆孔洞，其形状需要通过复杂的映射函数进行描述，对应的应力解析函数也十分复杂。对于双孔洞体系这种多连通域问题，Schwarz交替法局限于圆形孔洞体系问题的求解，而对于复杂形状多孔洞问题缺少有效的求解方法。为此，张路青等[26]利用孔洞边界坐标点的转换代替复应力解析函数的转换，根据不同孔洞的映射函数、逆映射函数以及孔洞相对位置关系对孔洞边界多余面力进行求解。LÜ 等[27]针对双直墙半圆拱形孔洞体系，通过傅里叶级数形式将多余面力的函数展开，并进行20 余次迭代，从而获得高精度的应力解析解。ZHANG等[28]借鉴此方法获得了无限域中含2个以上椭圆孔洞体系的应力场解析解。卞晓琳等[29]进一步结合复变函数解析拓延法，对2个相邻深埋隧道的应力场和位移场进行求解。以上研究极大推动了复杂形状双孔洞体系应力解析理论的发展，但由于非圆孔洞的逆映射函数十分复杂，特别是当孔洞形状与圆形差异较大时，运用现有方法求解应力函数时求解精度较低。

本文在Schwarz交替迭代法的基础上，提出一种新的理论解析方法。通过引入最优化技术，直接完成不同坐标系平面中孔洞边界坐标点的变换，无需在求解过程中引入逆映射函数，可避免逆映射函数求解造成的误差，在理论上可显著提升求解精度。基于此方法，以拱形孔洞为例，构建无限平面域含单拱形孔洞和双拱形孔洞体系的数学模型，获得拱形孔洞周边应力场分布规律，并利用数值模拟方法对解析结果进行验证与拓展。

1 基于交替迭代法求解双空洞体系应力场

1.1 交替迭代法求解双孔洞体系应力解基本原理

含任意形状双孔洞模型平面示意图如图1 所示。考虑弹性半空间内存在2个任意形状孔洞(孔洞1与孔洞2)且分布在任意位置，以孔洞1、孔洞2的形心为坐标系原点分别建立直角坐标系Z1(x1O1y1)和Z2(x2O2y2)，对应的映射函数分别为z1=ω1(ζ1)与z2=ω2(ζ2)(其中，ζ1与ζ2分别为含孔洞1 平面与含孔洞2平面在含单位圆映射平面上点的坐标，计算时使用复数形式ρeiθ，ρ为实部，i 为虚数，下同)。令远场水平应力、垂直应力与剪切应力分别为σx∞、σy∞与τx∞y，根据交替迭代法原理，孔洞2 应力求解过程如下。

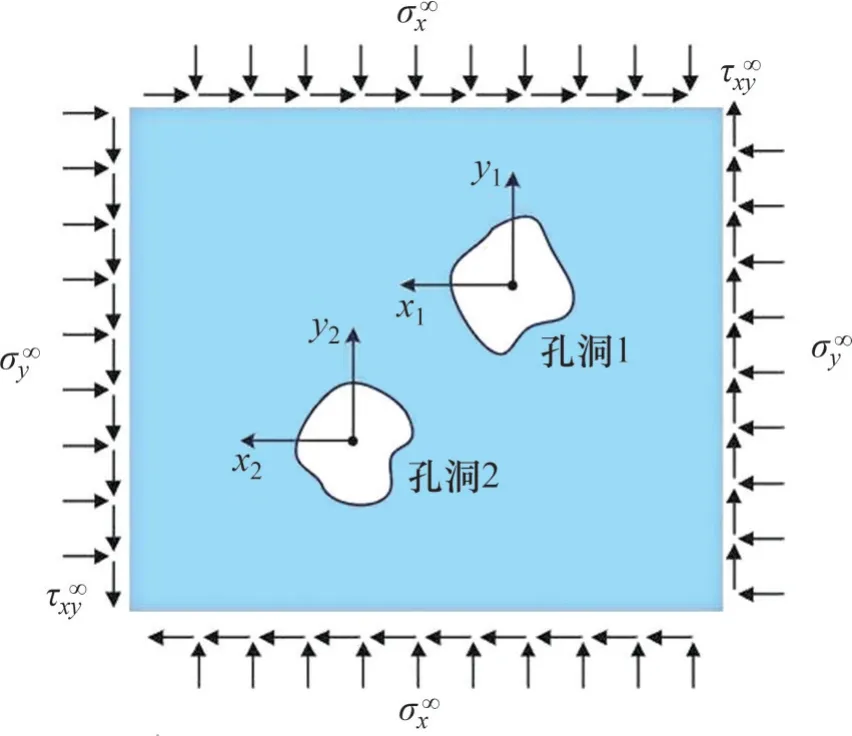
图1 含任意形状双孔洞模型平面示意图Fig.1 Schematic of a plate model containing two holes with arbitrary shapes

1) 假设当孔洞1 开挖完成时，孔洞2 尚未开挖，在远场应力作用下，只存在孔洞1的应力。

2) 计算坐标系Z1下孔洞1开挖后虚拟的孔洞2边界的多余应力。

3) 下一步开挖孔洞2时，必须给孔洞2边界施加外力以平衡孔洞1 在孔洞2 边界产生的多余面力。假设此时孔洞1不存在，将坐标系转为Z2，则可根据孔洞2边界应力平衡条件计算相应的应力函数，而此时孔洞2 又会在孔洞1 边界产生多余面力，需要再转换到Z1坐标系，计算新的边界平衡条件下关于孔洞1的应力函数。

随着迭代次数增加，某一孔洞在相邻孔洞边界产生的多余面力会越来越小，求解结果逐渐逼近真实结果。一般地，当求解精度满足实际要求时，便可停止迭代计算，完成应力求解。

1.2 逆映射函数未知情况下多余面力的求解

针对非圆形孔洞映射函数与逆映函数求解复杂、误差大等问题[30]，本研究提出在不考虑逆映射函数的情况下，采用交替迭代求解复杂形状双孔洞体系外部应力解析解的改进方法。

假设只存在孔洞1时，令解析函数为φ10(ζ1)与ψ10(ζ1)，则孔洞应力边界条件为

式中：σ1为ζ1平面单位圆周上点的坐标；t1为Z1坐标系下孔洞1边界上点的坐标，t1=ω1(σ1)/′(σ1)，其中′(σ1)为ω1(σ1)的共轭导数；(σ1)为φ10(σ1)的共轭导数；(σ1)为ψ10(σ1)的共轭。

φ10(ζ1)与ψ10(ζ1)可表示为

式中：φ01(ζ1)与ψ01(ζ1)可以通过Laurent 级数表示。常数B、B′与C′反映了远场围岩应力的情况。

求出解析函数φ10(ζ1)与ψ10(ζ1)的解后，需消除孔洞2 边界的多余面力，其核心问题是利用φ10(ζ1)与ψ10(ζ1)得到多余面力分布函数。在此过程中，需对ζ2平面的单位圆上点σ2进行坐标系变换，以得到孔洞2边界多余面力f112(σ2)：

式中：γ1为点σ2经过坐标系变换到ζ1平面中的对应点的坐标。

早期研究表明，对类圆形孔洞，由其逆映射函数得到的近似单位圆与实际单位圆基本吻合。然而，对于矩形、梯形、拱形等含棱角形状，其逆映射函数求解精度较低[29]。为此，本文引入低维变量最优化技术，通过不同平面与不同坐标系中采样点坐标转换，替代逆映射函数对σ2点对应的γ1点以及σ1点对应的γ2点进行坐标求解，最终得到对应的多余面力表达式，避免了逆映射函数的繁琐求解及与理论解之间的误差。下面以计算σ2点对应γ1点的坐标为例，对该方法步骤进行简要说明。

1) 确定孔洞2 对应单位圆上σ2点采样个数n，则采样间距(Δσ2)为Δσ2=2π/n。第j(j=1，2，3，…，n)个采样点的坐标为σj2=eiΔσ2×j。

2) 根据映射函数z2=ω2(σ2)确定σ2采样点在Z2坐标系中孔洞2边界上点t2的坐标。

3) 计算点t2在Z1坐标系中的对应点坐标η1=t2+c。

4) 利用最优化技术求解点η1在ζ1平面对应的映射点γ1，如图2所示。令初始域(图2中着色扇形区域)角度范围为[αa，αb]，半径范围为[ra，rb]。将初始域角度以0.5(αa+αb)为增量，半径以0.5(ra+rb)为增量，分为4 个子域，通过比较每个区域的端点值，确定最优值所在的子域(图中红色区域)。之后，再将子区域按照前面的方法分为4 个子区域，如此反复迭代，直至区域中心值达到设定的精度为止。

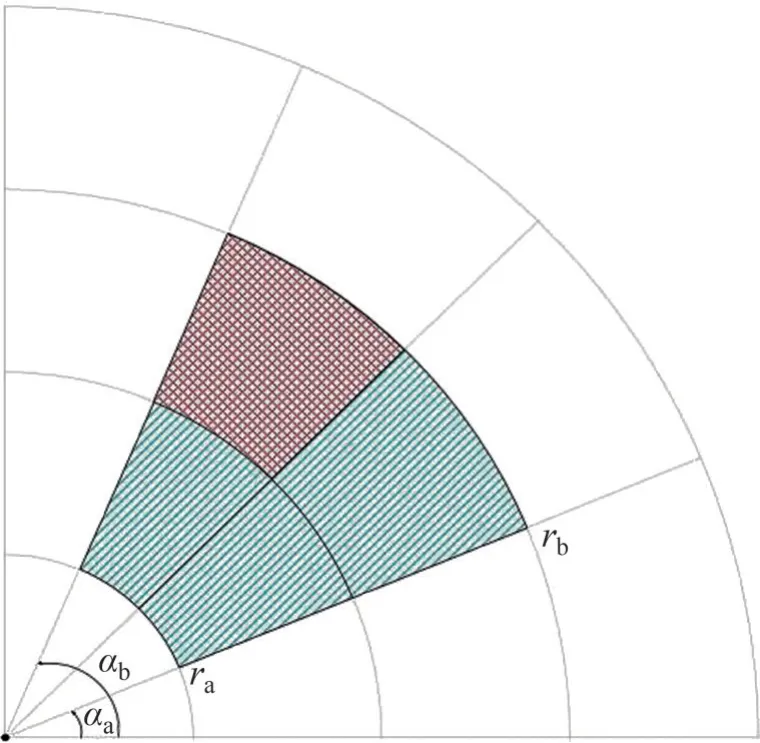
图2 利用最优化技术求解映射点坐标Fig. 2 Determination of mapping point coordinates by using optimization method

5) 依次确定采样点在ζ1平面中的坐标值，计算各点对应的多余面力。

同理，可根据以上步骤计算σ1点经过坐标系变换到ζ2平面中的对应点γ2，仅需改变相应的映射函数表达式即可。

当确定了孔洞采样点在映射单位圆上的多余面力之后，可利用傅里叶复数级数形式表示多余面力的分布。以f112(σ2)为例，令其傅里叶复数级数表达式为

将采样点坐标值代入式(5)，则可以建立高维方程组，求解可得f112(σ2)的傅里叶级数表达式。

1.3 复应力函数迭代求解

在确定f112(σ2)表达式之后，在第1次迭代计算中，孔洞2对应单位圆的应力边界条件可表示为

由式(6)求解得到的孔洞2 的应力解析函数φ12(ζ2)、ψ21(ζ2)与孔洞1 的应力解析函数φ10(ζ1)、ψ10(ζ1)叠加即可得到第1次迭代计算得到的求解结果，至此，任意形状双孔洞的第1次迭代完成。

由于迭代求解是从孔洞1开始的，故在第1次迭代后，孔洞2边界已满足零面力的边界条件，但孔洞1边界会产生新的多余面力f211(σ1)，故需要继续在孔洞1的边界施加新的反面力进行平衡，其计算过程与首次的迭代过程一致，在此后的每次迭代过程中，只需根据其上一步的迭代求解结果对双孔洞应力解析函数进行更新，直至两洞周边附加面力在要求范围之内。

2 算例分析与数值模拟验证

以岩体工程中常见的拱形隧道为例，利用提出的改进迭代求解方法计算双拱形孔洞围岩应力场，并采用有限元模拟对理论解析结果进行对比验证。随后，利用离散元软件PFC2D 对含双拱形孔洞围岩破坏模式进行分析。

2.1 拱形孔洞映射函数求解

以拱形孔洞为研究对象(图3)，其具体尺寸为：R1=6.30 m，R2=8.80 m，R3=1.60 m，R4=15.60 m，L1=12.25 m，L2=2.50 m，L3=4.64 m，L4=0.96 m，坐标原点为孔洞的形心。

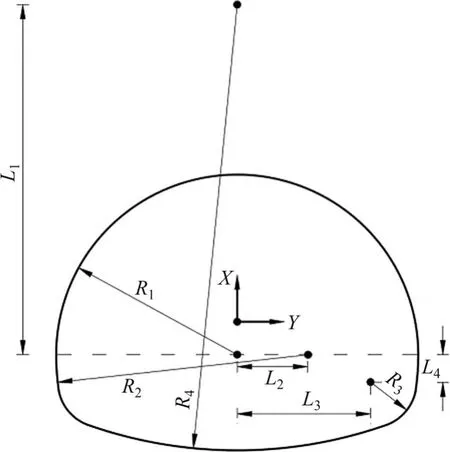
图3 拱形孔洞示意图Fig. 3 Schematic of an arched hole

Z平面上孔洞外区域变化到ζ平面上单位圆外区域的映射函数表达式为[30]

式中：R为实数，与Z平面上孔洞尺寸有关。当孔洞关于x轴对称时，Ck为实数，c为孔洞边界的积分路径。一般地，孔洞形状越复杂，就需要越大的k来提高映射形状的精度，即确定R和Ck后便可得到孔洞的映射函数。

令孔洞周边任一点Aj极坐标为(rj，αj)，其在ζ平面上单位圆上对应点Bj极坐标为(1，θj)，则由式(7)可得

由式(8)可得

根据欧拉公式，将式(9)中实部与虚部分开得：

对平面上单位圆上均匀分布的m个点进行采样，当孔洞自身关于x轴对称时，可只对范围为[0，π]的单位圆进行采样。令孔洞中心为坐标原点，Bj极坐标为(1，θj)，其通过式(11)确定的Z平面对应点Aj坐标为(rj，αj)，实际对应点A′j坐标为(r′j，αj)。此时，采样点与目标点的平均离差平方和f为

本文采用Box复合型最优化算法求解映射函数的系数。该算法的核心在于在n维空间可行域内构建具有N(N≥n+1)个顶点的多面体(又称复合形)，然后逐一比较复合形各顶点目标函数值。在每一步计算中，获取并删除复合形中使目标函数值最大的顶点(坏点)，同时生成使目标函数值更小的新点。如此反复迭代，使得复合形不断收缩，其顶点不断移向最优点，直至满足中止迭代条件，本文中设定的精度为5×10-4[31]。复合形法求解过程中孔洞映射形状的演化见图4。在迭代求解过程中，随着平均离差平方和f不断降低，根据复合形中当前最优点Xb得到的映射孔洞形状逐渐趋近于目标拱形孔洞形状。

图4 复合形法求解过程中孔洞映射形状的演化Fig. 4 Evolution of the mapping shape during the solving process using complex method

最终得到的拱形映射函数表达式为

根据式(13)得到的拱形孔洞映射形状与目标形状进行对比，见图5。从图5 可以看到：拱形孔洞的映射形状与实际形状高度吻合，证明了复合型最优化算法的适用性。

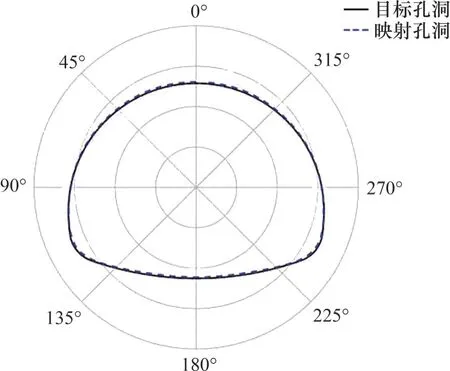
图5 孔洞映射形状与目标形状比较Fig. 5 Comparison between the mapping shape and original shape of the hole

2.2 双拱形孔洞体系应力场解析结果与数值验证

双拱形孔洞体系布局示意图如图6所示。双拱形孔洞体系以孔洞1形心为中心，两孔洞形心距为9 m，两孔洞形心连线与水平线夹角(下称连接角)为θ。为研究两孔洞连接角的影响，取θ的范围为0°～90°，以15°间隔递增。令σx∞=p，σy∞=τx∞y=0，利用本文提出的改进迭代求解方法计算双拱形孔洞周边应力分布。

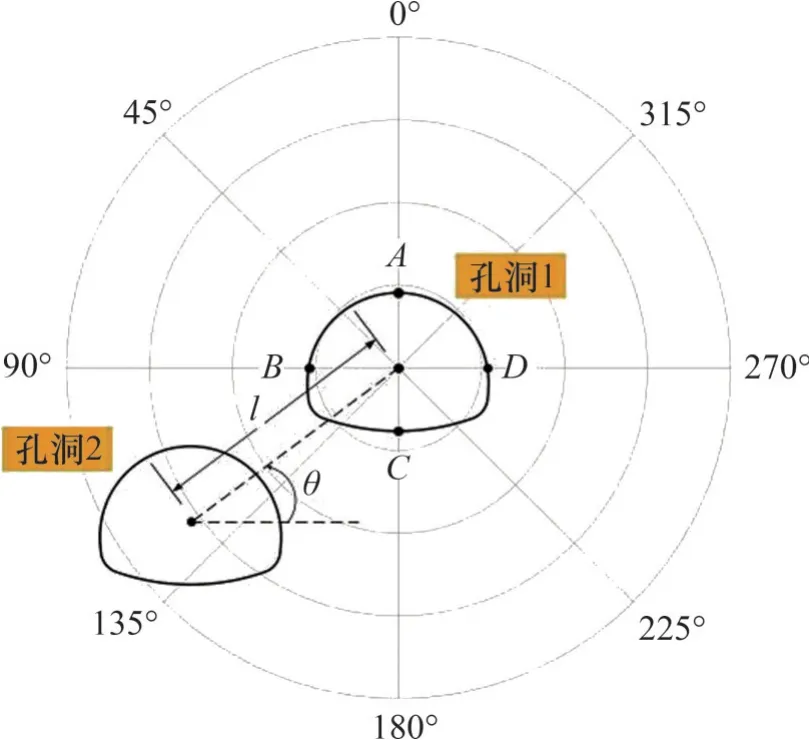
图6 双拱形孔洞体系布局示意图Fig. 6 Schematic of the two arched holes system

为验证应力场解析解的准确性，采用有限元分析软件ANSYS建立二维平面应变模型，获得侧压系数为0时的双拱形孔洞应力分布规律，并将其与理论解析结果进行比较。模型中，围岩材料选用线弹性本构模型，单元类型为PLANE183 平面单元，岩层弹性模量取5 GPa，泊松比取0.3，垂直方向远场应力σx∞取1 MPa。为减少边界效应的影响，模型尺寸需大于孔洞尺寸的10 倍，故平面数值模型的尺寸设为300 m×300 m。

当θ为0°时，孔洞1周边环向应力的分布规律(以压应力为正)见图7。从图7 可见：整体上，理论解析与数值模拟结果变化趋势近乎一致，这说明本文提出的双孔洞应力解析解方法是准确、可靠的。值得注意的是，在局部位置，特别是左右边墙底端拐角处解析结果与模拟结果存在很小的差异，其原因是：一方面，在数值模拟中，孔洞并不是处于无限域之中，边界对孔洞周边应力场可能会产生一定影响；另一方面，受计算精度影响，映射形状与目标拱形孔洞形状也并不完全吻合，但这种差别很小，可以忽略不计。

图7 孔洞1周边环向应力分布理论解析与数值模拟结果比较Fig.7 Comparison between analytical and numerical results of stress around the hole 1

2.3 连接角对孔周应力分布的影响规律

在无侧压情况下，单拱形孔边界以及双拱形孔体系中孔洞1边界环向应力分布随连接角θ的变化见图8。图8 中，位于孔洞外部的应力为正，即为压应力，反之则为拉应力；红点和绿点分别表示最大压力、拉应力所在位置。

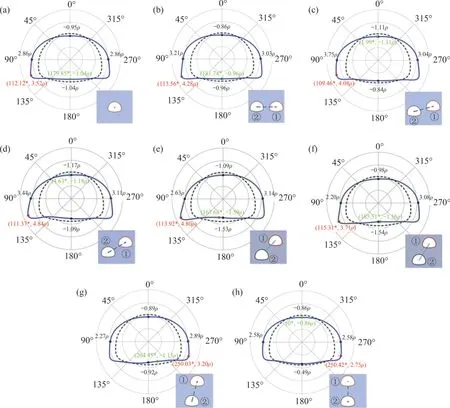
图8 单孔洞与不同布局双孔洞体系中孔洞1边界环向应力解析解Fig.8 Hoop stress results around the boundary of a single hole and hole 1 in the two-hole system with different layouts

由图8(h)可见：当连接角θ为90°时，孔洞1边界的切向应力呈对称布置；但在其他角度下，孔洞2的存在影响孔洞1周边应力的对称性；当连接角为0°～60°时，孔洞1环向最大压应力在孔洞左侧拱底位置，而当连接角为75°时，孔洞1 左侧拱底环向压力显著降低，最大压应力出现在孔洞右侧；随着连接角的变化，孔周最大拉伸应力位置会在孔洞顶、底中心位置附近变动，但无明显变化规律；当连接角为0°、45°、60°、75°时，最大拉应力在孔底中心位置附近，而在其他角度下，最大拉应力在孔顶中心位置。此外，从图8还可见：当2个孔洞沿斜线布置时，靠近相邻孔洞一侧与远离相邻孔洞一侧的边界应力呈现明显的差异；在靠近孔洞2 的侧边(如左侧边墙和孔底)，环向应力随连接角变化明显，而在远离孔洞2 的侧边(右侧边墙和孔顶)区域，应力变化幅度相对较小，说明相邻2个孔洞之间的相互影响主要集中在相邻一侧的区域。

双拱形洞体系中孔洞1最大解析拉、压应力集中系数随着θ的变化规律见图9。由图9可见：

1) 随着θ增加，双拱形洞体系孔1周边最大拉伸应力集中系数先增大后减小；当θ为45°时，孔洞1的顶板区域拉应力达到最大。

2) 最大压应力随着θ增加表现出先降低、后增加再快速降低的变化趋势；当θ为30°时，孔洞1边界切向压应力达到最大，此后逐渐降低，直到θ为90°时，切向压应力集中系数最小，仅为2 个孔水平布置时(θ=0)的64.2%。

2.4 连接角对双拱孔洞体系承载特性与破坏模式的影响

离散元数值仿真可通过微观尺度研究孔洞周边的微裂纹的萌生和演化，从而反映出孔周应力场的分布情况。为研究连接角对双拱孔洞体系承载特性与破裂模式的影响，本文采用离散元软件PFC2D开展含双拱形孔洞体系岩体数值模拟。孔洞形状、尺寸及其布局均与理论求解中的模型一致，模型长×宽为100 m×100 m，侧压系数为0(如图10所示)，竖直方向以恒定速率加载直至模型完全被破坏。采用PFC2D模拟时，首先以某砂岩为参照对象，基于该砂岩标准单轴压缩试验结果对数值模型微观参数进行标定，各参数取值如表1所示。图11 所示为砂岩室内试验单轴压缩试验与数值模拟结果。从图11可见：数值模型除了无压密阶段外，其强度和弹性模量都与室内试验结果一致；同时，在破坏模式上，两者都属于斜剪切破坏，这说明可利用表1中参数很好地模拟砂岩的力学行为。

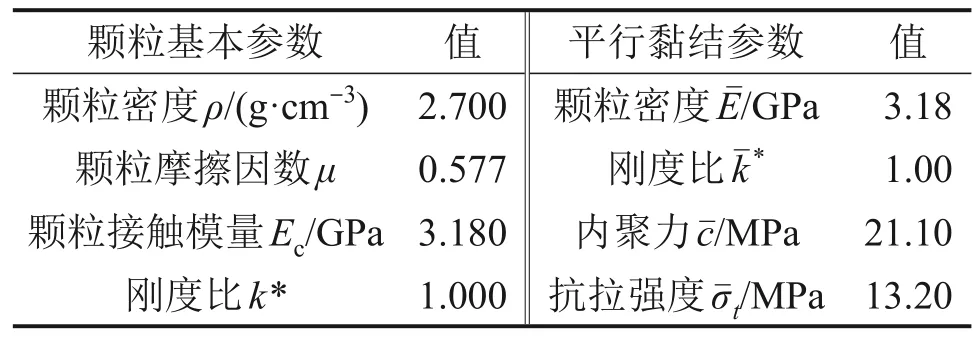
表1 PFC2D离散元数值模型微观参数Table 1 Micro-parameters for the PFC2D numerical model

图10 离散元数值模型Fig.10 Discrete element numerical models

图11 数值模型标定结果Fig.11 Calibration results for numerical model

数值模拟中含双拱形孔洞试样峰值应力随连接角θ的变化规律见图12。从图12可见：随着θ增加，试样的峰值应力在15°时增加，随后降低；当θ超过30°时，试样的峰值应力持续增加。双拱形孔洞体系峰值应力与应力集中系数的关系见图13。从图13 可见：随着压应力集中系数增加，峰值应力呈单调降低的趋势；红色虚线为峰值应力与压应力集中系数线性拟合曲线，较高的确定系数(0.907)表明可用线性函数表征两者的联系；而拉应力集中系数，与峰值应力无明显关系，这说明含双孔洞岩体的破坏主要受压应力集中系数控制。

图12 双孔洞模型峰值应力随θ的变化Fig.12 Variation in the peak stress of numerical model containing two holes against θ

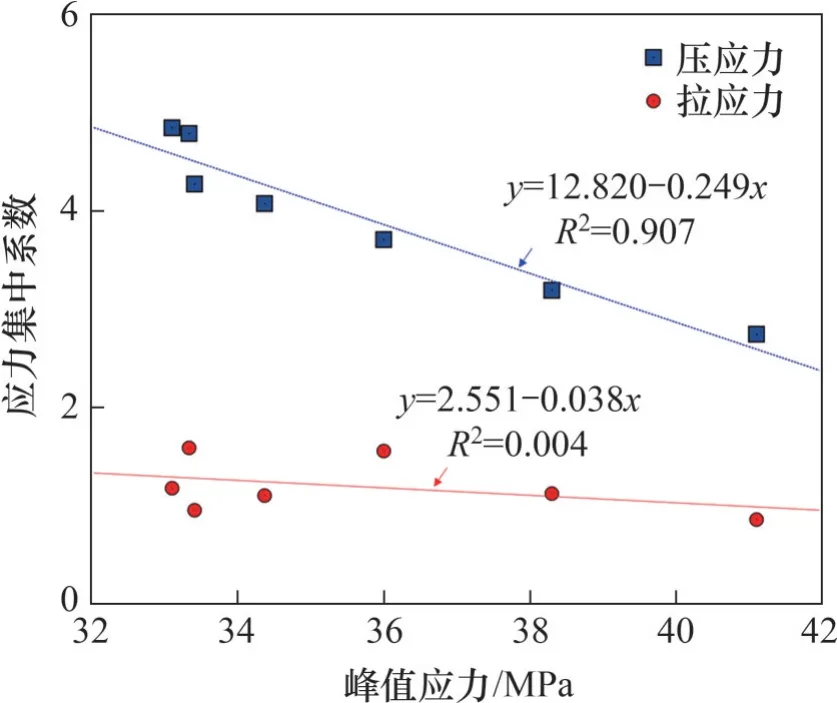
图13 双拱形孔洞体系峰值应力与应力集中系数的关系Fig.13 Relationship between the peak stress and stress concentration factor in the twin arched hole system

PFC模拟中含拱形孔洞围岩破坏模式见图14。图14 中，红色点代表裂纹，蓝色圆圈表示岩石起裂位置。含单孔洞围岩裂纹萌生于最大拉应力集中的底板中心位置(图14(a))，主裂纹从孔洞顶底部中心沿着竖直方向延伸。对于双孔洞围岩，破裂主要发生于2个孔洞连接处，起裂位置、破坏程度均与连接角有关；当θ为0°或90°时，2个孔洞间的裂纹方向与加载方向平行，其贯通模式属于拉伸破坏。然而，当2个孔洞倾斜布置时，其破坏属于剪切破坏或拉/剪混合破坏。值得注意的是，当θ为30°时，初始破坏出现在理论计算中孔洞1 边界最大压应力所在位置附近，但该区域的破坏并未随着初始破坏的出现而继续发展，而是在2个孔洞的顶板或底板的拉伸裂纹发展到一定程度后才出现剪切贯通破坏。而对于其他角度，起裂位置均发生在孔洞顶底部(即拉应力集中处)，但与中心位置略有偏移，这是第2孔洞的存在对应力分布造成的影响(见图8)。

图14 孔洞周围区域破坏模式Fig.14 Failure patterns around the hole

3 结论

1) 利用最优化技术进行不同平面和坐标系下孔洞边界坐标点的变换，直接求解孔洞边界的多余面力分布函数，实现了地下2个任意形状孔洞在任意相对位置下的应力求解。该方法无需进行逆映射函数的繁琐求解，避免了逆映射函数求解造成的误差，适用于任意双孔洞形状和布置情况，降低了计算难度并提高了求解精度。

2) 邻近孔洞的存在会改变现有孔洞边界切向应力分布，加剧应力集中程度，其主要影响区域为靠近相邻孔洞的一侧。对于拱形孔洞，在单轴压缩条件下，当连接角θ到达30°时，孔洞边界切向应力的压应力集中程度达到最大；而θ为45°时，其拉应力集中程度达到最大。

3) 理论计算与数值模拟结果表明，在单轴压缩条件下，孔洞体系的初始萌生裂纹为孔洞顶底板拉应力集中区域形成的拉伸裂纹，但最终破坏表现为双孔洞间的贯通破坏。不同连接角的双孔洞体系峰值应力与压应力集中系数呈线性相关关系，说明双孔洞岩石的破坏取决于孔洞边界的压应力集中程度。