长江经济带生态经济效率时空差异特征及驱动因素

李思迪，贾彬彬，钟永德，任 腾

（中南林业科技大学a.旅游学院；b.物流与交通学院，长沙 410004）

0 引言

目前由沿海地带和沿江地带共同组成的“T”字型空间架构已经成为中国经济增长最具潜力的两大区域，长江经济带作为其中唯一横跨东、中、西三大地区的一级发展轴线，推动其高质量发展具有重大意义[1]。长期以来，长江经济带部分地区依赖能源、化工等产业的传统发展模式实现了经济高速增长，同时也为其带来了生态环境方面的负面影响。为此，习近平总书记在2016—2020年相继于重庆、武汉和南京主持召开长江经济带发展座谈会，提出了“坚持生态优先、绿色发展”的战略定位，努力实现以生态环境保护来推进经济社会发展。在此背景下，如何协调好生态、经济和社会之间的关系，实现以最小的生态资源消耗获取最大的经济和社会产出，争取生态经济效率的最大化，是现阶段社会各界所面临的重要问题。

推动区域生态经济发展首先需要准确把握区域生态经济发展现状及发展趋势，而生态经济效率作为全面考虑生态环境、经济增长、社会福利等因素的一种综合指标，能够有效衡量区域生态经济发展水平[2]。现有相关研究普遍认为虽然生态、经济和社会系统的性质与功能互不相同，但其各自的生存和发展却是相互联系的，因此须视其为一种复合系统，即生态-经济-社会复合系统[3,4]。由于该复合系统存在多投入、多产出的特征，因此，近年来学者们普遍运用数据包络分析（DEA）方法测算区域生态经济效率[5—7]。

早期的相关研究往往将决策单元的各子系统视为平行结构，不考虑其相互作用关系，多运用单阶段DEA模型对其展开效率评价。之后，部分学者从博弈角度出发，通过构建矩阵型DEA[8]、网络DEA[9]等模型来刻画复合系统中各子系统间的合作关系。然而，上述模型皆是基于当期截面数据通过逐年测算的方式计算各年内的相对效率，不利于纵向分析效率的动态变化情况[10]。因此，韩晶和陈曦（2021）[11]从动态角度出发，将Malmquist 指数引入DEA 评价框架中。上述做法虽然考虑了时间序列带来的影响，但仍存在一定局限性，即全要素生产率指数用于表征两个时期间的变化趋势，无法从全周期视角来分析效率的变动情况。相比而言，全局DEA 模型以全周期投入产出数据构造的全局生产可能集为共同参考系，避免因基期选择的不同而造成的差异，同时能够缓解因单期异常数据而导致的效率结果不稳健问题。

综上所述，目前国内外学者关于区域生态经济效率评价领域取得了丰富的研究成果，但仍存在一些不足：一方面，以往关于生态经济效率评价的研究往往忽略了生态子系统在区域发展战略中的优先地位，仅简单地将生态-经济-社会复合系统中各子系统视为平行结构，且大部分研究尚未考虑子系统之间的双向反馈特性，导致所得效率值可能存在误差；另一方面，现有研究中多利用当期截面数据以逐年测算的方式进行效率计算，因此无法从全周期的视角对区域生态经济效率展开纵向分析。鉴于此，本文首先在考虑反馈关系的基础上剖析了生态-经济-社会复合系统中各子系统之间的相互作用关系，以此探究其内部结构特征；其次，为使不同时期间的效率值具有纵向可比性，基于全局DEA 理念构建考虑反馈特性的全局BLP-DEA模型对长江经济带生态经济效率测算；然后，借助Dagum基尼系数和核密度估计探究其时空差异特征；最后，利用Tobit模型对其驱动因素展开分析。

1 研究设计

1.1 考虑反馈特性的全局BLP-DEA模型构建

根据“生态优先”的发展战略，长江经济带生态-经济-社会复合系统的发展目标应是希望在生态优先的基础上，实现经济-社会子系统的高质量发展。受此启发，本文将生态子系统作为上层系统，将经济子系统与社会子系统所构成的经济-社会子系统作为下层系统。此外，为了更加全面地刻画生态-经济-社会复合系统的内部结构特征，本文除了考虑上层系统对下层系统的作用联系之外，还考虑了下层系统对上层系统的物质反馈，即将经济-社会子系统所取得的环境改善成果作为反馈变量投入生态子系统中，具体如图1所示。

图1 考虑反馈特性的生态-经济-社会复合系统示意图

假设在研究周期内共有T(t=1，…，T)个时期，每个时期皆有n个决策单元。对于t时期的第j个决策单元DMUj(j=1，…，n)，和分别表示其生态子系统的投入和非期望产出；和分别表示其经济-社会子系统的外部投入和期望产出；作为中间变量，其既是生态子系统的期望产出，也是经济-社会子系统的投入；而作为反馈变量，其既是经济-社会子系统的期望产出，也是生态子系统的投入。

本文考虑反馈特性的生态-经济-社会复合系统的特征，运用Leader-Follower 模型刻画生态子系统和经济-社会子系统的主从关系，构建了考虑反馈特性的全局BLP-DEA 模型，其中下层系统的优化模型中部分约束由上层系统的优化模型的求解结果确定。根据以上分析，以生态子系统为Leader，经济-社会子系统为Follower，假设规模报酬不变，构建以投入为导向的考虑反馈特性的全局BLP-DEA模型，具体如式（1）和式（2）所示：

上层系统：

下层系统：

式（1）中βe和γk、σi和αw分别为上层系统中相应投入和产出的权重，式（2）中σi和ξq、δc和γk分别为下层系统中相应投入和产出的权重，其中中间变量权重σi和反馈变量权重γk皆由上层系统决定。生态经济效率则由上下层系统效率值以0.5为权重加权求和所得，由此可知，当且仅当上下层系统效率值皆为1 时生态经济效率才能为1，即表现为DEA有效，否则视为无效。

1.2 核密度估计

核密度估计作为一种非参数检验方法，能够基于给定样本集合以连续密度函数曲线详细刻画随机变量的形态、位置和延展性特征，因此被广泛运用于变量的动态分析中，具体计算公式如式（3）和式（4）所示。其中，f(x)为随机变量x的密度函数，K(u)为核函数，h、N、Xi分别为带宽、观测值个数和独立同分布观测值。

1.3 Dagum基尼系数及其分解

为从空间视角探究长江经济带生态经济发展水平的差异特征及其来源，本文利用Dagum基尼系数对长江经济带及各地区生态经济效率的基尼系数展开测算，具体公式如下：

式（5）中，长江经济带生态经济效率总体基尼系数（G）可分解为地区内差异贡献（Gw）、地区间净值差异贡献（Gnb）和超变密度差异贡献（Gt），可分别由式（9）、式（11）和式（12）计算得出。其中，ρji（ρhr）表示j(h)地区中i(r)省份的生态经济效率；α表示长江经济带三大地区的生态经济效率总体均值；αh表示h地区的生态经济效率均值；n表示长江经济带包含的省份个数；nj表示j地区包含的省份个数；k表示地区个数；式（13）中，Djh表示j和h地区之间生态经济效率的相对影响。将djh定义为j和h地区之间的生态经济效率差值，可理解为j和h地区中所有ρ ji-ρhr＞0 的样本值总和的数学期望，见式（14）。将pjh定义为超变一阶矩阵，可理解为j和h地区中所有ρhr-ρji＞0 的样本值总和的数学期望，见式（15）。式（14）和式（15）中，Fj（Fh）表示j(h)地区的累积密度分布函数。

1.4 Tobit模型

为探究长江经济带生态经济发展的关键驱动因素，本文从环境规制、城镇化水平、地区开放程度、地区科技水平、产业结构等方面展开驱动因素研究。其中，被解释变量（Y）选取所求的2010—2019年长江经济带各省份生态经济效率值，解释变量依据上述五个方面选取如下：（1）环境规制（ENR）选择各省份环境污染治理投资总额占地区生产总值的比重来衡量；（2）城镇化水平（UR）选取城镇化率来衡量；（3）地区开放程度（FDI）选取各省份的外商直接投资来衡量；（4）地区科技水平（TI）选取各省份的专利申请授权数来衡量；（5）产业结构（IND）选取第三产业增加值与地区生产总值的比值来衡量。由于生态经济效率的取值范围受限于(0,1]，因此本文选择Tobit模型进行驱动因素分析。此外，为减少多重共线性和量纲的影响，本文对上述部分解释变量进行对数化处理，式（16）和式（17）分别为当期变量、滞后一期变量的Tobit回归模型。

其中，i代表地区，t表示年份，α为方程中的常数项，εit为随机干扰项，Y表示生态-经济-社会复合系统效率值。

1.5 指标体系构建及数据来源

本文通过对区域生态经济的投入产出过程特征进行分析，依据指标体系的构建原则，借鉴相关研究构建如下生态经济效率评价指标体系[12—15]，如表1所示。

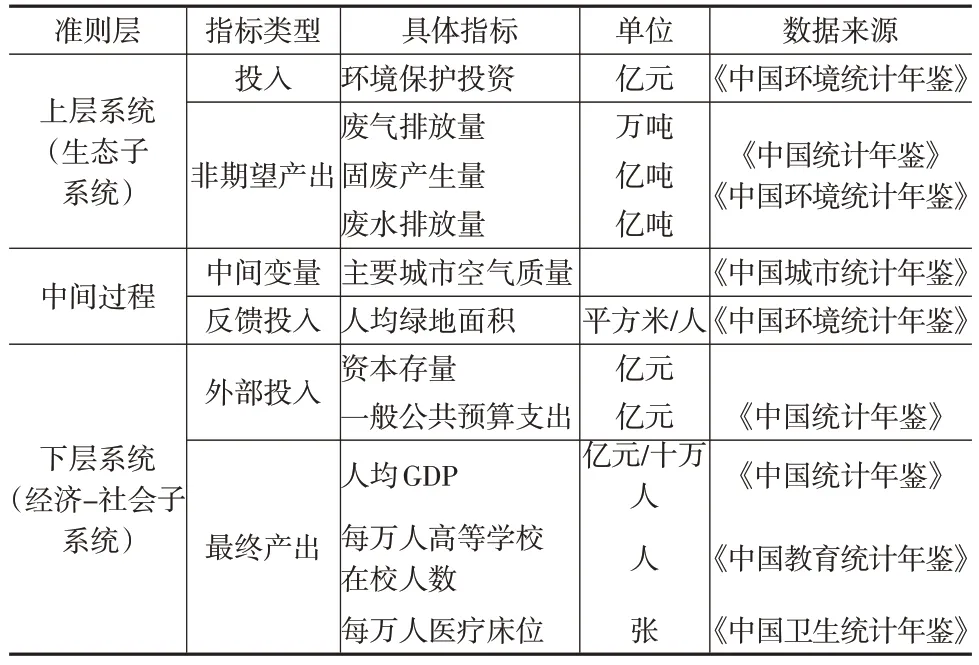
表1 生态经济效率评价指标体系

结合数据的可获得性和可比性，本文选取2010—2019 年长江经济带11 个省份为评价对象，并依据相关研究的普遍做法，将重庆等4 个省份划分为上游地区，将湖南等4个省份划分为中游地区，将浙江等3个省份划分为下游地区。值得说明的是，由于我国并未公布各省资本存量的相关数据，因此本文依据永续盘存法进行计算。

2 实证分析

2.1 长江经济带生态经济效率总体特征

由于式（1）和式（2）皆为非线性规划模型，难以直接求解，因此本文先用C-C 变换方法将其转化为线性规划模型，再利用MATLAB软件进行求解，结果如表2所示。

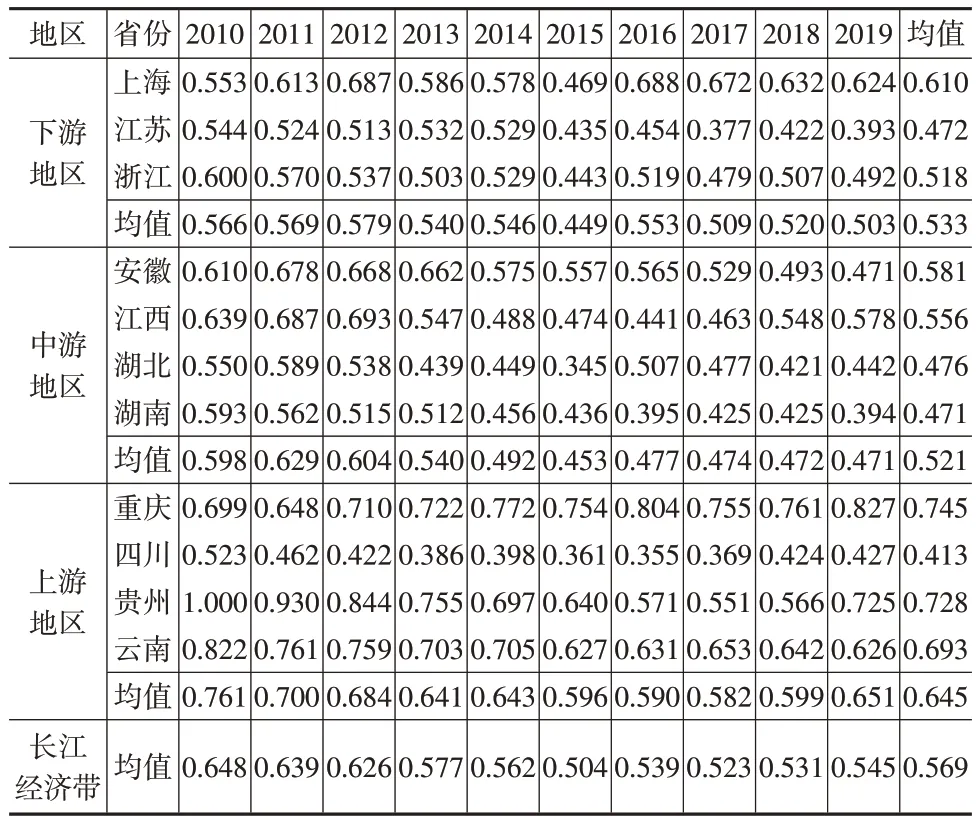
表2 2010—2019年长江经济带生态经济效率

由表2可知，2010—2019年长江经济带生态经济效率均值为0.569。从效率的时序变化特征来看，2010—2019年长江经济带生态经济效率总体呈现波动中略微下降趋势，由2010 年 的0.648 下 降 到2019 年 的0.545，降 低15.9%。值得注意的是，2016—2019年长江经济带生态经济效率实现了稳步回升。从效率的空间分布来看，2010—2019年重庆的生态经济效率居于领先地位，贵州、云南和上海紧随其后，四川、湖南、江苏等省份排名相对靠后。整体而言，长江经济带各省份之间的生态经济效率存在显著差异，并呈现上游地区、下游地区、中游地区依次递减的分布格局。

2.2 长江经济带生态经济效率分布动态

本文基于生态经济效率测算结果，利用核密度估计方法对长江经济带生态经济效率的动态分布特征展开进一步分析，结果如图2所示。

图2 2010—2019年长江经济带生态经济效率的核密度曲线

由图2可知，2010—2019年长江经济带生态经济效率核密度曲线的变化区间先缩小再扩大，说明长江经济带生态经济效率整体差异有所扩大。核密度曲线的主峰高度在上下波动之中，总体呈现主峰高度下降，波峰宽度则逐渐减小，这说明各省份生态经济效率的绝对差异近年来有扩大趋势。此外，图2 中核密度曲线存在尾部抬升现象，形成“一主一次”两峰并立的格局，说明长江经济带生态经济发展存在微弱的两极分化态势。具体而言，在2010 年与2013 年，次峰高度逐渐上升，尤其以2013 年最为明显，说明两极分化态势逐渐凸显，但在2015年、2017年及2019年，次峰高度渐趋平缓，说明两极分化态势得到明显减缓。

2.3 长江经济带生态经济效率的空间差异及分解

为从空间视角进一步分析长江经济带生态经济效率的差异特征，本文对长江经济带生态经济效率Dagum基尼系数及其分解系数进行计算，结果如表3所示。

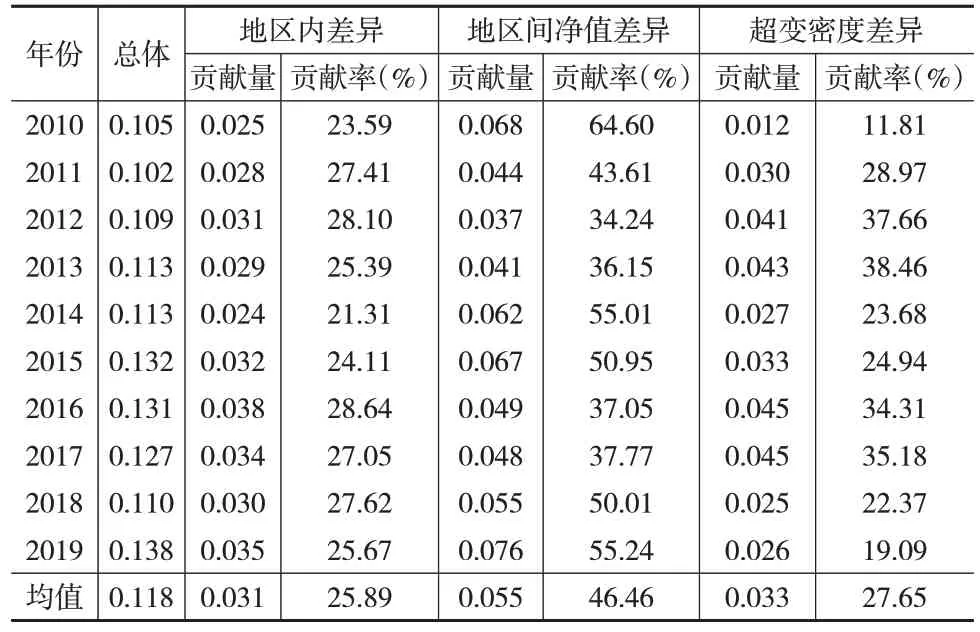
表3 长江经济带生态经济效率Dagum基尼系数及其分解

总体来看，长江经济带生态经济效率Dagum基尼系数以2011 年、2015 和2018 年为转折点呈现“先减后增再减再增”的“W”型变化趋势，并于2019 年达到最大值（0.138）。该现象表明在研究期内，长江经济带的生态经济存在非均衡性发展，且其差异呈扩大趋势。

从差异来源来看，长江经济带各地区内部生态经济效率基尼系数的变化较为平稳，对总体差异的贡献率保持在25.89%左右；各地区间的生态经济效率基尼系数分别以2012 年、2015 年、2017 年为节点，呈现“W”型的波动变化趋势；超变密度在2010—2017年呈现递增趋势，其贡献率由11.81%增加至35.18%，但在2017 年后递减，其贡献率降低至19.09%。总体而言，在研究期内超变密度贡献率呈现“M”型变化趋势。2010—2019 年的各分解系数的均值显示，超变密度均值为0.033，对总体差异的贡献率为27.65%；各地区之间的差异贡献量为0.055，对总体差异贡献率为46.46%；地区内差异贡献量为0.031，对总体差异贡献率为25.89%。以上分析说明地区之间的差异是长江经济带生态经济效率总体差异的主要来源。

2.4 驱动因素结果分析

本文运用Stata 软件，运用Tobit 回归模型对长江经济带及其上、中、下游地区生态经济效率的当期与滞后一期的驱动因素展开实证分析，结果如下页表4所示。

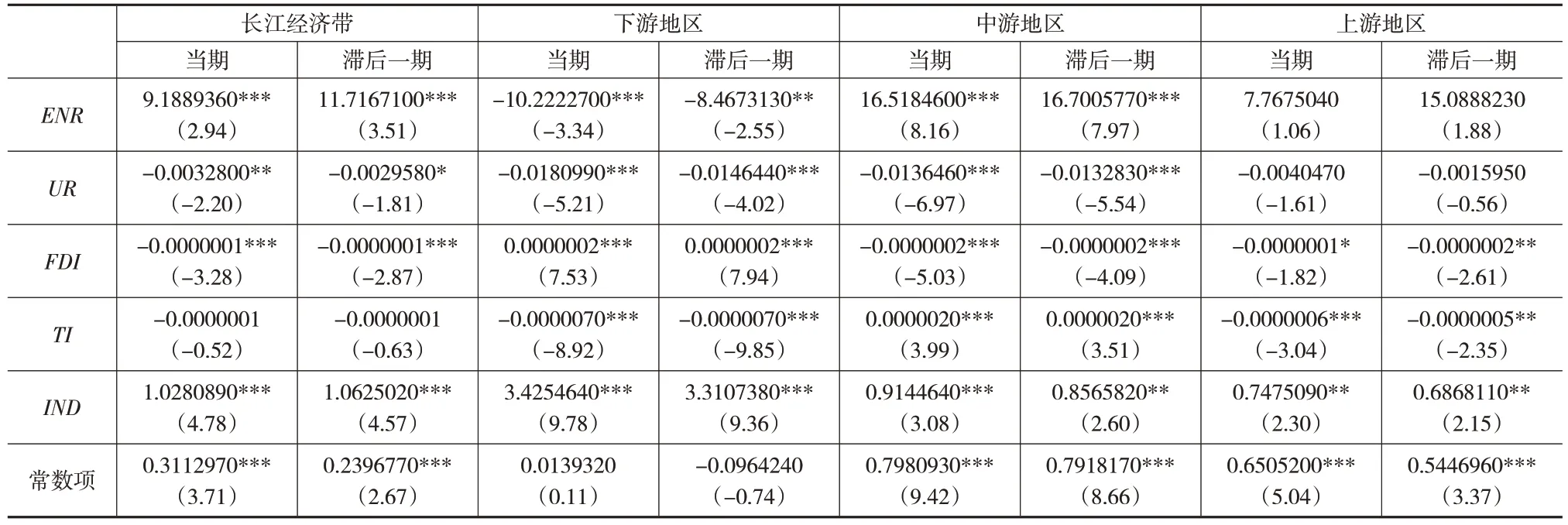
表4 长江经济带及各地区生态经济效率的驱动因素回归结果

由表4可知，（1）整体来看，环境规制和产业结构对长江经济带当期和滞后一期的生态经济效率皆具有显著的正向促进作用，且环境规制对滞后一期的生态经济效率影响的回归系数高于当期，而产业结构对滞后一期及当期的生态经济效率影响的回归系数相差较小，说明前者的滞后影响强度更高，而后者的影响不仅具有即时性，还具有同等强度的滞后性。此外，城镇化水平和地区开放程度和对长江经济带当期和滞后一期的生态经济效率皆具有显著的抑制作用。（2）从各地区来看，在下游地区，环境规制、城镇化水平和地区科技水平对当期及滞后一期的生态经济效率产生了显著的抑制作用，地区开放程度和产业结构产生了显著的促进作用。在中游地区，环境规制、地区科技水平和产业结构对当期及滞后一期的生态经济效率产生了显著的促进作用，城镇化水平和地区开放程度则抑制了其发展。在上游地区，地区开放程度和地区科技水平对当期及滞后一期的生态经济效率具有抑制作用，而产业结构对其却具有正向的促进作用。环境规制和城镇化水平并未通过显著性检验。

3 结论

本文在考虑反馈特性的基础上首先详细刻画了生态-经济-社会复合系统的内部结构特征，并据此构建考虑反馈特性的全局BLP-DEA 模型对2010—2019 年的长江经济带及其上、中、下游地区的生态经济效率展开评价，然后借助Dagum 基尼系数和核密度估计从多维角度对其时空差异特征进行挖掘，最后利用Tobit 回归模型揭示其驱动因素，得到结论如下：

（1）从总体特征来看，2010—2019 年长江经济带生态经济效率均值为0.569，总体处于中等偏上水平。其中，生态经济水平发展良好的省份基本分布于上游地区，零星分布于下游地区，发展相对落后的省份则连片集中分布于中游地区。

（2）从动态分布来看，2010—2019 年长江经济带生态经济效率总体呈下降趋势，并以2016 年为节点，表现出“逐渐下降”“保持平稳”两个阶段。此外，核密度曲线“一主一次”两峰并立的格局说明长江经济带生态经济发展存在微弱的两极分化态势，次峰的高度和宽度随着时间的推移呈现波动减小的趋势，表明两极分化现象得到缓解。

（3）从空间差异特征来看，长江经济带生态经济效率在空间上形成上游、下游、中游地区依次递减的发展格局。长江经济带各地区生态经济效率内部差异变化相对较为平稳，而各地区之间生态经济效率差异和超变密度差异皆处于波动变化之中。总体而言，长江经济带的生态经济效率空间差异存在扩大趋势，其中地区之间的效率差异是导致其扩大的主要来源。

（4）从驱动因素来看，环境规制是推动长江经济带生态经济发展的重要原因，对提升长江经济带生态经济效率具有显著的促进作用；城镇化水平对长江经济带生态经济效率具有显著的抑制作用；地区开放程度对长江经济带生态经济效率具有显著的抑制作用，但却促进了下游地区的生态经济发展；地区科技水平对长江经济带下游、上游地区的生态经济发展具有显著的抑制作用，对中游地区的生态经济发展具有促进作用；产业结构对长江经济带及各地区皆存在显著的促进作用。