融合类信息的函数型矩阵填充方法与应用

高海燕，马文娟，薛 娇

（1.兰州财经大学 统计与数据科学学院；2.甘肃省数字经济与社会计算科学重点实验室，兰州 730020）

0 引言

智能交通系统（ITS）是缓解交通拥堵、提高交通效率的有效途径。收集和分析车辆平均速度、车辆流量、平均车道占用率等实时交通监控数据，不仅能快速发现交通异常，方便交通管理，而且挖掘数据潜在特征信息有助于提高交通管理运行效率和道路通行能力。交通数据在ITS建设中具有至关重要的作用，是交通分析、规划与设计的基础。然而，由于临时软件或硬件故障、维护操作、探测器构造、传输失真以及在ITS中传输期间数据包丢失等原因使得交通设备（如环路检测器）收集的数据往往不完整[1]。这些缺失值不仅影响交通实时监控，还会影响数据挖掘、推断预测等数据分析的性能。因此，交通监控数据中缺失值的准确插补具有重要价值和现实意义。

针对数据缺失问题，学者们提出了诸多缺失插补方法。“均值类”插补方法[2,3]（如均值插补、中位数插补、众数插补等）以及K 近邻算法[4]的插补性能有限。当数据高度集中时，热卡插补法[5]填充效果差，并在模拟数据的分布特征时缺乏准确性。多重插补[6]考虑了缺失数据的不确定性，插补效果虽好但计算量巨大，不适用于处理大规模缺失数据。基于最大似然估计（MLE）的方法[7,8]中，如概率主成分分析（PPCA）采用特定的参数模型，可以同时实现模型拟合和缺失数据插补，但在估计模型参数时，由于EM（Expectation Maximization）算法的固有特性，当缺失率较高时，PPCA插补效果较差[9]。基于回归的插补方法试图构建从已知属性到缺失属性的映射函数。其中局部最小二乘（LLS）插补[8]最为典型，当出现大规模缺失时，LLS 插补精度不高。近年来，矩阵填充技术在机器学习领域得到了充分发展[10,11]，其目标是根据观测数据对缺失数据进行预测和恢复，用以处理矩阵数据的大规模缺失问题。与其他插补方法相比，矩阵填充技术的插补精度更高[6]。然而，经典的矩阵填充把样本看作一个整体，潜在地假设所有样本数据同等重要，更加强调样本的共性，从而忽略样本数据内的复杂结构，不可避免地降低了矩阵填充的性能。

随着交通流数据采样频率的增加，其函数的特性变得越来越明显。大规模交通流数据的外在表现形式虽是离散、稀疏的片段点集，但内在结构却呈现连续、动态的函数曲线（或曲面）特征。因此，函数型数据分析方法（Functional Data Analysis，FDA）[12]被广泛用于交通流数据的研究中[1,13]，能够充分考虑交通数据相邻时间、相邻探测器之间的相关特征信息以及变化轨迹的潜在模式[14]。FDA 在处理缺失数据时具有优势，它放松了数据采集的结构约束和分布设定，能够从交互的函数视角深层次挖掘数据潜在的动态信息。函数型数据缺失处理的一种策略是忽略缺失数据，在对数据分布进行假定的基础上对包含缺失值的数据直接进行建模分析。这种做法属于纵向数据分析方法，常采用混合效应模型，利用EM 算法进行处理；另一种策略是将缺失数据补齐，进而针对完整数据展开分析。当缺失规模较大时，函数型数据缺失处理可以转化为曲线轨迹预测问题，进而转化为矩阵填充问题。在一定条件下，函数型数据修复问题等价于秩约束的矩阵填充问题[15]，可通过对基函数施加连续型约束，并对观测数据矩阵使用稀疏矩阵分解技术来进行处理[16]。Kidziński 和Hastie（2018）[16]将矩阵填充和函数型数据拟合相结合，为函数型数据的缺失插补提供了两种实现方法——SFI、HFI。然而，当面临非负函数型数据时，以上缺失插补方法不能保证结果非负，限制了这些方法的适用范围。

本文试图构建非负函数型数据缺失处理的修复方法，通过引入非负约束，在函数型数据分析视角下，借助非负矩阵分解（Nonnegative Matrix Factorization，NMF）和类信息，提出融合类信息的函数型矩阵填充方法（Functional Matrix Completion Method with Class Information，CFMC）。CFMC 方法不仅考虑样本数据之间的时空相关性以及潜在变化模式，还在整体学习框架下集成融合每条样本的多个插补结果，可以进一步提高插补性能。

1 交通流量数据插补问题的描述

设每天每个环路检测器监测到的交通流轨迹为受测量误差污染的随机函数的实现，表示为L2(T)中的随机函数X，其中L2(T)表示封闭时间间隔T上平方可积函数的Hilbert 空间。假设yij（i=1，2，…，n;j=1，2，…,m）为函数xi(t)的第j个离散观测值，由以下一般形式的回归模型生成：

xi(t)可以在有限维度下近似表示为：

其中，ϕi(t)=[ϕi1(t)，ϕi2(t)，…，ϕir(t)]T是给定空间中的一组基，αi=[αi1，αi2，…，αir]T是待估系数列向量。为了方便表示，将式（1）和式（2）改写为矩阵形式：

式（3）中，Y为函数型数据矩阵，Φ∈Rm×r为基矩阵，A=[α1，α2，…，αn]∈Rr×n为待估系数列向量形成的矩阵，E为误差矩阵。式（4）中，ϕ(t)是统一表示各交通流曲线的基函数，曲线向量x(t)中元素之间的差异由系数矩阵A决定。

假设共有交通检测器M个，交通流量数据采集时间间隔为Δt，采集天数为d天，则交通流量样本曲线总数n=M×d，观测时间j=m1=m2=…=mn=m，观测值个数N=n×m。定义为第i条交通流量样本曲线观测时间点的集合，i=1，2，…，n，S={ti1，ti2，…，tim}为第i条样本曲线的已观测时间点。假设第i条样本曲线xi有观测值{(tij，yij)，j=1，…，m}，则缺失值的观测时间点集合为͂=S/Si。交通流量数据缺失插补可由曲线轨迹预测问题转化为矩阵填充问题，故本文交通流量缺失插补问题可视为基于观测矩阵Y，通过观测值集合{yij|i=1，2，…，n，j∈S}预测缺失值集合

由于交通检测点的分布不同以及人们的出行行为具有一定的规律性，因此各交通流量变化轨迹之间存在显著的差异，考虑时空相关性，距离越近的检测点同一时间段的观测数据之间相关性越强。样本之间的相关性是缺失值插补的重要依据[17]，类内的交通流变化轨迹越相似、样本之间的相关性越高，则局部的类内信息越有助于提高插补准确性。

2 融合类信息的函数型矩阵填充方法

2.1 融合类信息的函数型矩阵填充方法框架

为了处理非负函数型数据缺失插补问题，本文在函数型数据分析的框架下，充分考虑不同样本之间的潜在差异、挖掘样本之间的时空相关性，提出融合类信息的函数型矩阵填充方法（CFMC）。首先，构造函数型矩阵填充模型进行初始插补，以获取完整数据集；其次，利用聚类分析探索相关性强的同质子群，将具有相似变化轨迹的样本划分到同一类中；然后，对每一类样本利用类间信息进行插补；最后，利用集成学习方法将不同类别下每条样本的插补结果融合，得到最终的插补值。CFMC方法具体实现步骤如下：

步骤1：构建函数型矩阵填充模型（Functional Matrix Completion Model，FMC）对含缺失值的观测矩阵Y进行初始插补。

针对非负函数型数据缺失情况，引入非负约束，融合非负矩阵分解、矩阵填充等思想，构建函数型矩阵填充模型FMC：

其中，Y∈Rm×n为函数型数据的离散观测矩阵，O∈Rm×n是与Y同型的投影矩阵，即若Y中的条目可观测，则Oij=1；否则Oij=0。Φ∈Rm×r为通过B-样条基函数 形成的 基 矩 阵，U∈为NMF 的 非 负基矩 阵，V∈为NMF 的非负系数矩阵，m为原始数据的变量数（维数），n为样本量，r为曲线拟合基函数的数量，p为NMF的秩。FMC算法的具体执行过程见下页表1。

表1 FMC算法

步骤2：通过聚类划分引入样本类信息，使得每一类样本相似度尽量高，并借助类内样本相关性插补缺失值。

借助聚类结果挖掘函数型数据样本曲线的时空相关性，进一步提升插补精度。由于每一类中的样本相关性较强、具有相似的变化轨迹，因此在每一簇样本中利用FMC方法进行局部缺失填充，类内样本的高相关性有助于提高FMC 方法的插补精度。具体地：（1）对步骤1 中的矩阵V应用函数型聚类算法（FNMF），将样本划分为k类(k=1，2，…，K)，设最终聚类结果为{C1，C2，…，CK}；（2）对每个同质子群Ci应用FMC 方法，得到对应第i类的插补结果并将k个插补结果排列组合为Ŷk；（3）重复过程（1）和（2），直到k=K。最终得到Y的多个插补结果，记为

步骤3：采用自加权集成学习算法动态赋权计算出最终插补值。

不同的聚类数k会得到不同的插补结果，为充分利用不同聚类里的插补结果以及降低k的影响，本文采用自加权集成学习算法动态赋权对K个插补结果进行融合，得到最终的插补结果̂。以第l条样本曲线为例，将样本Y·l的K个插补结果融合得到最终的插补结果，满足：

其中，ωk为权重，定义，根据聚类数为k时插补值与真实值的误差动态调整。求解式（6）的优化问题，得样本Y·l的最终插补结果为：

CFMC方法在FMC方法初始插补的基础上，考虑交通流量样本的相关性，利用函数型聚类算法挖掘同一路网中交通流量样本的时空相关性，嵌入类内信息，使得类内样本相关性强，在有效利用全局数据特征的同时保留更多的局部信息。与FMC方法利用全局数据特征信息插补缺失值的优异表现相结合，由于NMF 的非负约束性与类内局部特征信息的提取，因此相比其他插补方法，CFMC 方法有更好的解释性和准确性。此外，CFMC方法采用自加权集成学习算法，不仅降低了聚类数k对插补结果的影响，还对每条样本曲线的多个插补结果进行融合，有助于进一步提高插补的有效性。

2.2 时间复杂度分析

FMC方法的时间复杂度主要体现在U和V的更新迭代中。对于U的更新，需要O(2mnr+2nrp+mrp+mnp+rp)加法运算、O(2mn+2mnr+2nrp+mrp+mnp+rp)乘法运算、O(rp)除法运算。则在一次迭代中，更新U的时间复杂度为O(2mn+4mnr+4nrp+2mrp+2mnp+3rp) 。同理，更新V的时间复杂度为O(mn+6mnr+6nrp+3np)。故FMC 方法迭代一次的时间复杂度为O(mn+mnr)，当迭代次数为t时，时间复杂度为O(t(mn+mnr))。在CFMC方法中，当执行K个FMC 局部填充时，时间复杂度为O(Kt(mn+mnr))。

3 交通流量数据实例应用

3.1 数据集

为了评估CFMC方法的插补性能，本文在实例数据集中进行模拟插补实验。数据来源于公共交通数据集PeMS（http://pems.dot.ca.gov）美国加州路网中6 个检测站①美国加州路网中的6个检测站ID分别为：716421、716424、716440、716442、718155、716453。2014年5月和6月的交通流量数据。检测器采集数据的时间间隔Δt为5min，每天每条数据包含m=288 个观测值。考虑到交通流量在节假日与正常工作日之间有显著差异，故不考虑节假日，只分析正常工作日的交通流量数据，为便于比较，选取不含缺失值的连续30天观测值，交通流量数据样本总数n=180。

3.2 对比方法与评价指标

本文利用实例数据集验证所提CFMC 方法的有效性和优越性。为便于比较，对完整数据集随机生成缺失值，缺失率P分别设置为15%、20%、30%、40%、50%、60%、70%。本文将10种常用插补方法作为对比方法，分别是传统多元插补方法，包括均值填充、线性插值、K 近邻算法、热卡填充、MICE；函数型插补方法，包括SFI[16]、HFI[16]、PACE[1]、FM[1]以及步骤1中的FMC方法。同时，采用3个广泛使用的定量指标来评估插补性能：均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）。具体计算公式为：

其中，n0是包含人工缺失条目的曲线轨迹数，mi是第i条曲线轨迹的缺失点数，ti*j是第i条曲线轨迹第j个生成缺失的时间点。RMSE、MAE以及MAPE越小，说明方法的插补精度越高，性能越好。实验主要通过R 4.1.3 实现，实验的计算机环境为：Intel（R）Core（TM）i5-5200U CPU＠2.20 GHz，内存6GB，Windows 10 64位操作系统。

3.3 交通流量数据相关性分析

基于皮尔逊相关系数（r）计算不同交通流量样本之间的相关性大小，如图1所示。观察图1可知，交通流量数据具有较强的正相关性，且相关系数实际分布在一个较大范围（[0.4,1]）内。说明对于不同检测器和工作日，交通流量样本的相关性波动较大。随机选取一条测试样本，并寻找与其最相关以及最不相关的样本，结果如图2所示。测试样本与最相关和最不相关样本之间的皮尔逊相关系数分别为0.993 和0.366，显然，最不相关样本的变化轨迹呈现更复杂的形状，说明不同样本之间的变化模式有显著差异。基于交通流量样本之间的相关性划分不同的类别，类内样本具有相似的变化模式，相关性较大，最相似的样本对于缺失值插补能提供更可靠的信息。

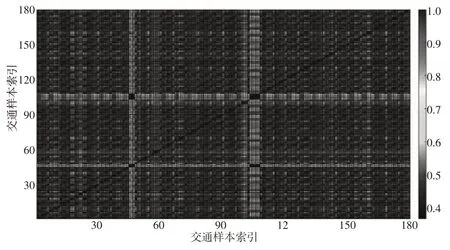
图1 样本间皮尔逊相关系数矩阵

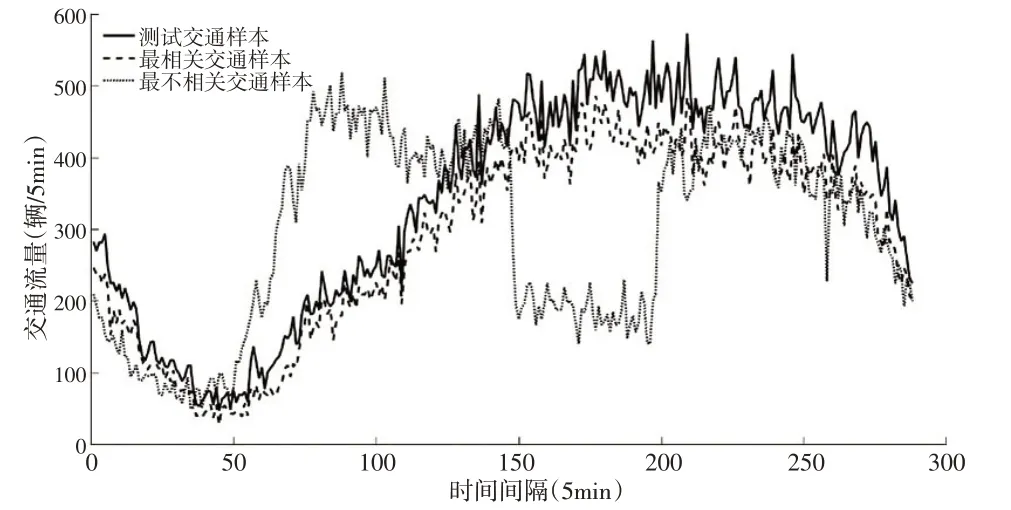
图2 最相关和最不相关交通样本

3.4 聚类数的确定与聚类结果展示

在CFMC方法中，聚类数k对缺失值的插补有显著影响。k值越小，类内样本方差越大，填充缺失值时可用相关信息越少，导致插补误差越大；反之，k值越大，聚类数越多，类内样本方差越小，且各样本相关性越强，但同时也使类内样本数减少，进而影响FMC 算法的插补性能。此外，为说明CFMC 算法中集成学习的有效性，还需研究无集成学习（即只进行步骤1和步骤2）时填充方法的插补性能，故在不同缺失率下，分别比较所提方法在无集成学习与有集成学习时，插补性能随聚类数k的变化，如图3 所示。观察图3 可知，无集成学习时，插补误差随k的增大而减小，但当k超过某一值时，插补误差逐渐增大，表明过多的聚类数反而会增大方法的插补误差，降低插补性能；而有集成学习时，插补误差随k的增大不断减小，集成不同的插补结果比单一聚类数下的插补误差更小，意味着自加权集成学习算法显著提高了插补精度。实验测试结果表明，当k=9 时插补误差趋于平稳，故确定CFMC方法在交通流量数据插补实验中的聚类数为9。

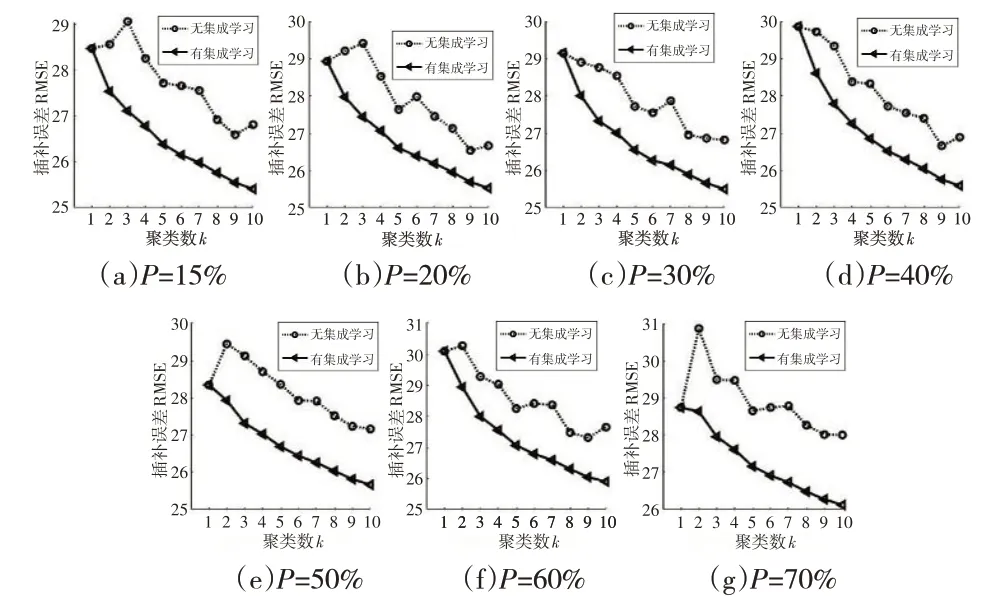
图3 不同缺失率下插补误差RMSE随聚类数的变化曲线

为进一步说明交通流量样本之间的相关性以及存在的潜在差异，选取9类中的3类可视化展示其部分样本，如图4所示，一横排代表一类。从图4可以更加直观地看到，不同类别之间交通流量样本的变化趋势、达到车流量早晚峰时间以及持续时间等有显著差异，而同一类样本的变化模式更相似，样本轨迹基本相同。因此，聚类结果展示了预期的效果，即类间差异大、类内差异小。

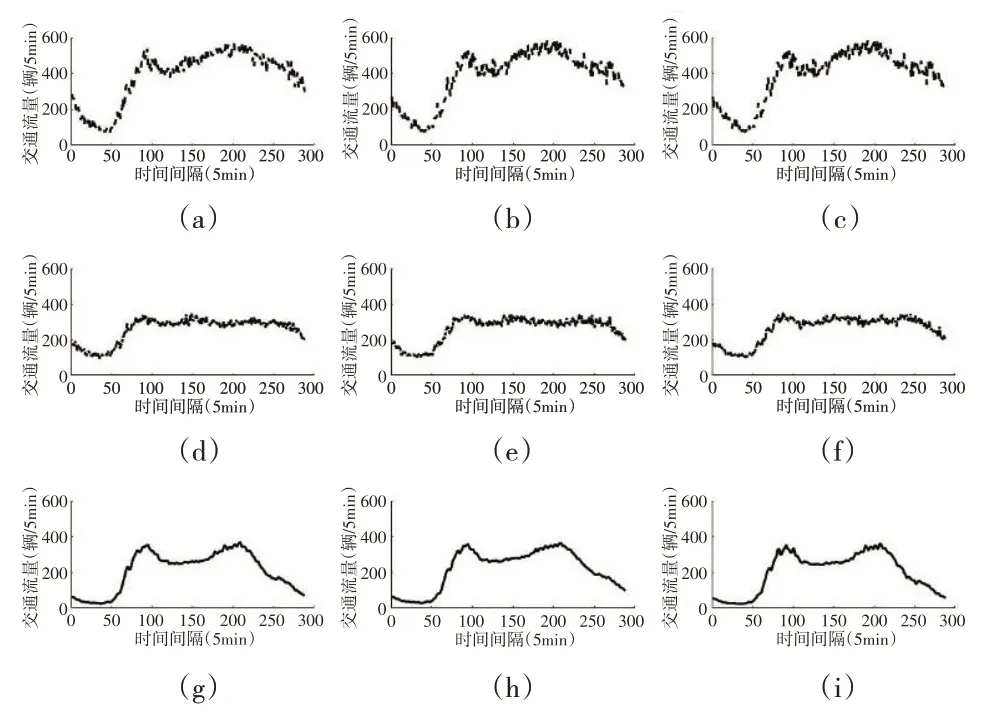
图4 CFMC方法聚类的部分结果

3.5 插补结果分析

不同缺失率下交通流量数据的插补结果如下页表2、表3和表4所示，可以得到以下结论：

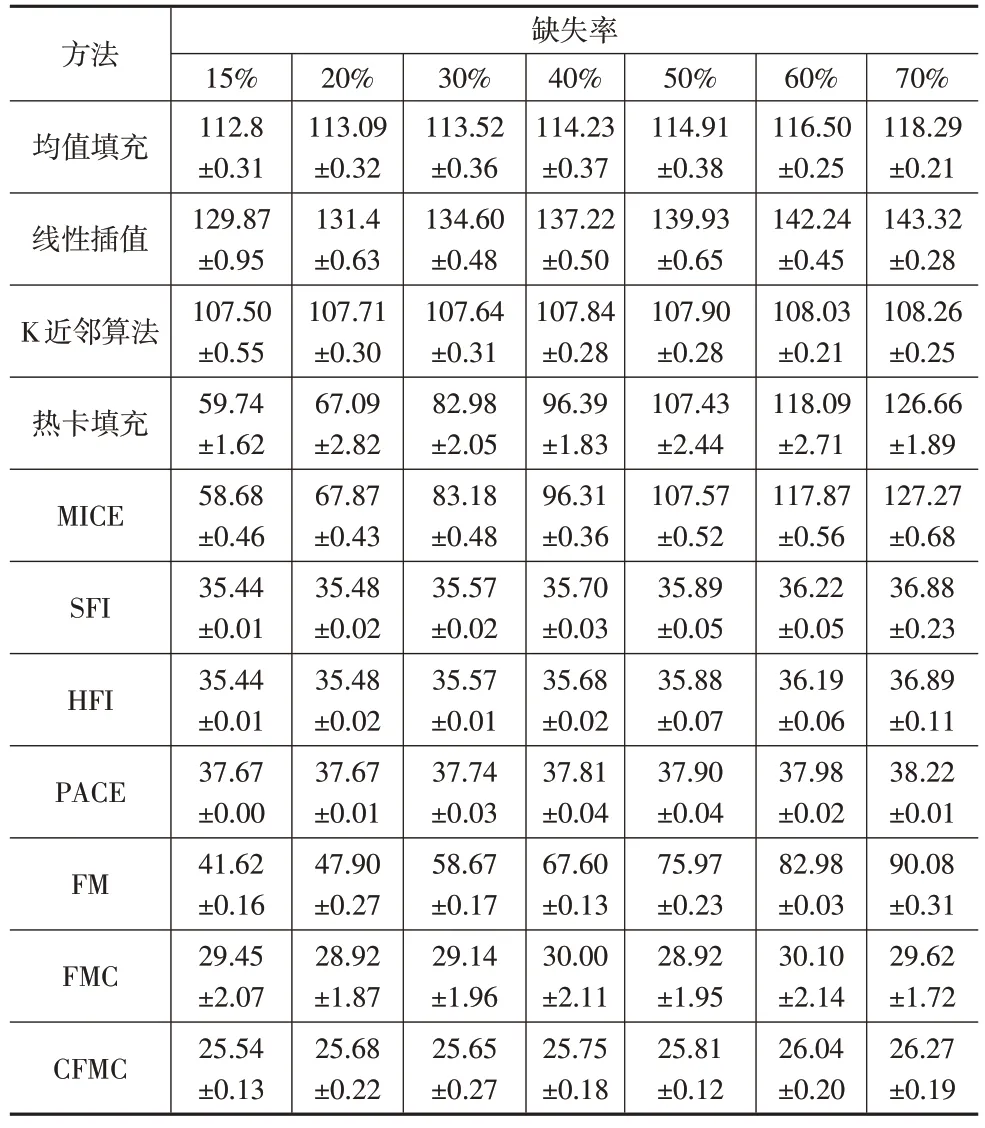
表2 不同缺失率下RMSE结果(10次重复模拟结果均值±标准差)

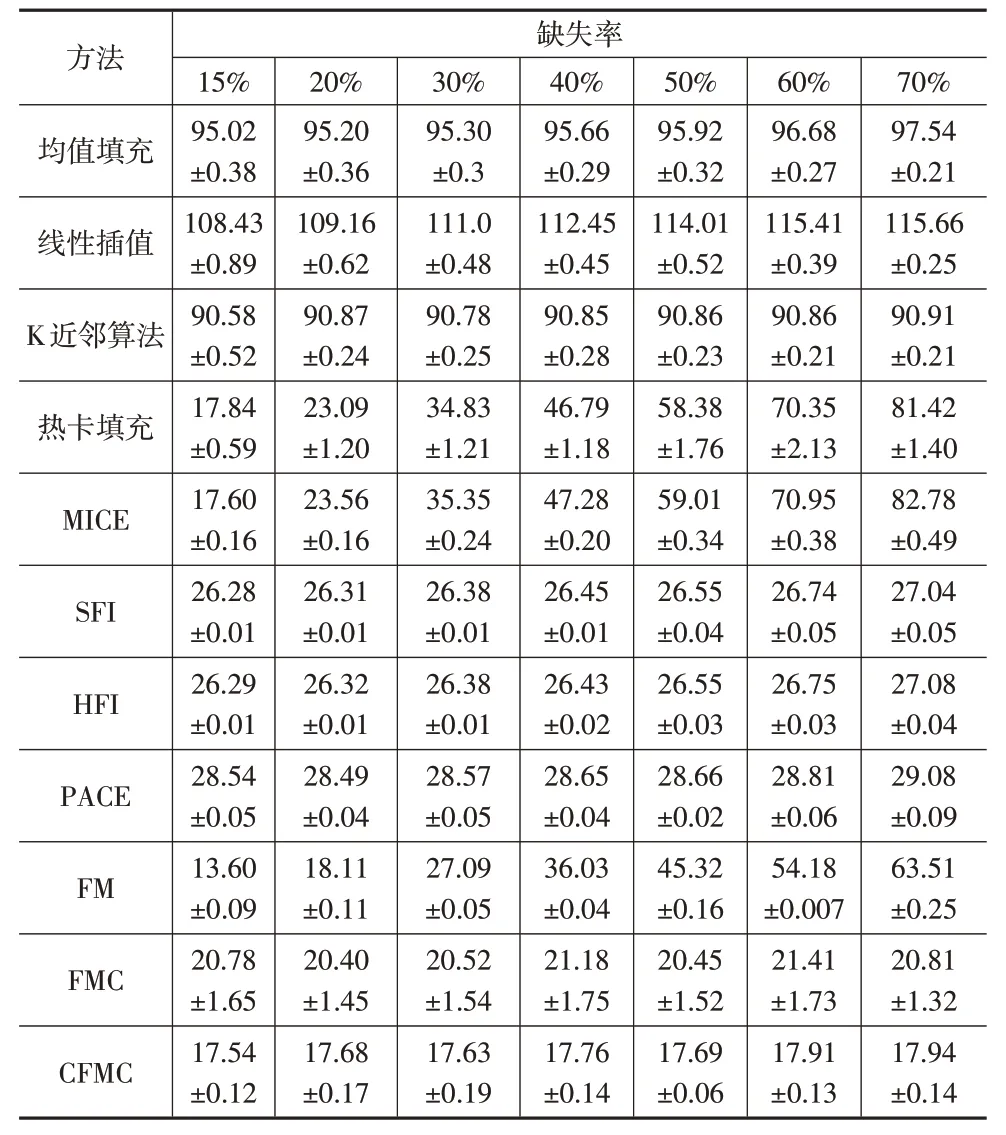
表3 不同缺失率下MAE结果(10次重复模拟结果均值±标准差)

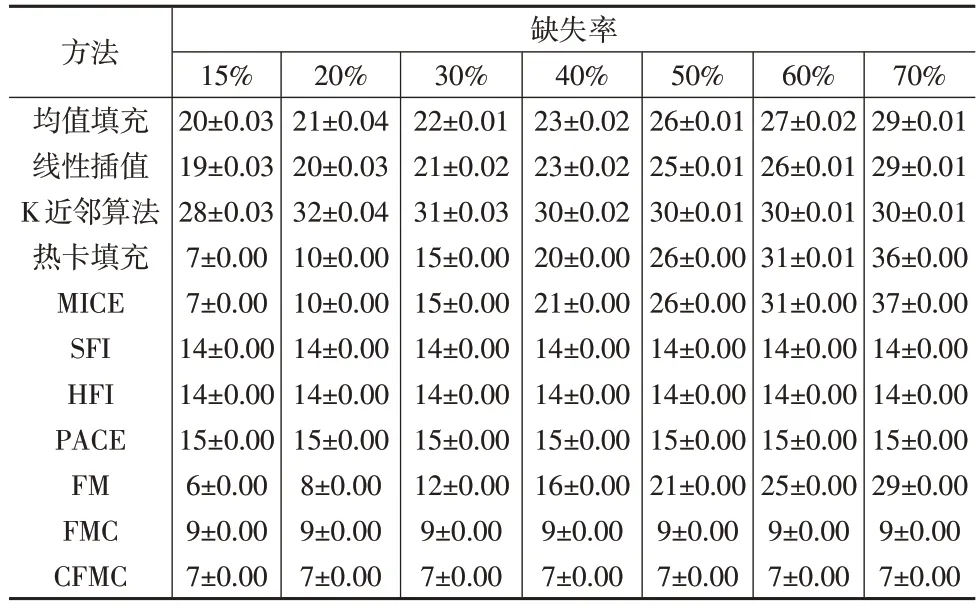
表4 不同缺失率下MAPE（%）结果（10次重复模拟结果均值±标准差）

（1）传统多元统计插补方法中热卡填充、MICE的插补性能显著优于均值填充、线性插值、K近邻算法，然而热卡填充、MICE 的插补误差受缺失率的影响较大，鲁棒性差；在所有缺失率下，均值填充、线性插值的RMSE 均高出K近邻算法4.93%～32.38%，其原因在于这两种方法没有充分考虑到交通流样本曲线之间的相关性。

（2）函数型插补方法SFI、HFI、FPCA、FM 以及FMC 方法的插补误差均低于传统多元统计插补方法，说明这5种方法在插补交通流函数型数据时具有一定的优越性。同时，由于FMC方法融合了函数型数据分析、矩阵填充以及非负矩阵分解等思想，因此其RMSE 比SFI、HFI、FPCA、FM低16.90%～67.11%，插补性能在5种方法中最优。

（3）不同缺失率下CFMC 方法的RMSE 均显著小于其他缺失值插补方法，插补性能最优。此外，相较于FMC方法，CFMC 方法利用集成学习将多个插补结果进行融合，RMSE 显著降低了10.75%～14.16%。因此，通过探索交通流数据的潜在变化模式，利用样本曲线之间的相关性以及差异性填充缺失值，并对不同插补结果进行集成学习，可以显著提高CFMC方法的插补性能。

（4）为了进一步比较插补性能，分别计算插补方法的RMSE、MAE、MAPE 曲线下面积（Area Under Curve，AUC）作为度量指标[1]：

此处PL=0.15，PU=0.70。各个插补方法的AUC 插补误差如图5 所示。观察图5 可知，相较于其他方法，CFMC 方法的AUC 误差最小，FMC 次之，说明整体上CFMC方法的插补精度优于其他方法。

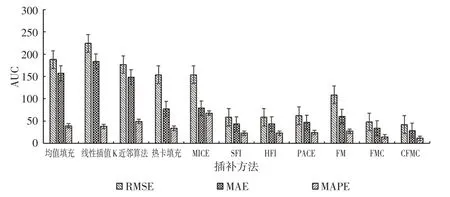
图5 不同插补方法的AUC误差

（5）对比表2、表3、表4 可以发现，所有插补方法的插补误差RMSE、MAE、MAPE 均随着缺失率的增多而增大，说明函数型数据出现大规模连续缺失对缺失值的插补影响较大。通过观察可以发现，CFMC方法的插补结果在所有缺失率下都十分稳定，RMSE、MAE、MAPE 平均变化仅为0.47%、0.37%、0.00%，故所提CFMC方法受缺失率P的影响较低，鲁棒性较好。

（6）不同缺失率下各个插补方法运行一次的时间消耗如表5 所示。观察表5 可知，虽然CFMC 方法相较于均值填充、线性插值、K 近邻算法、热卡填充耗时显著增加，但相比于MICE、PACE、FM 优势显著，其中不同缺失率下经典函数型插补方法PACE、FM 处理一次缺失值耗时为CFMC 方法的40.27～199.98 倍。实验表明，CFMC 方法相比其他方法插补精度更高，且处理时间可控，故CFMC 方法在处理大规模缺失数据方面具有显著的优势。

表5 不同缺失率下各插补方法运行一次的时间消耗 （单位：min）

4 结束语

为了处理交通流量数据的缺失问题，本文提出一种融合类信息的函数型矩阵填充方法（CFMC），通过类信息挖掘交通流量数据的相关性，并利用相似样本填充缺失值可以提高插补性能，同时应用自加权集成学习算法融合不同聚类数下的插补结果有助于进一步提高插补方法的精度。本文还以公共交通数据集PeMS 中车流量数据为例，验证了CFMC方法的插补能力。结果表明，针对不同的缺失率（15%～70%），与K 近邻算法、MICE、PACE 等10 种插补方法相比，本文提出的CFMC 方法具有优越性，能够保证插补的有效性和准确性。均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）这3个量化指标分别降低了10.75%～81.69%、0.34%～84.48%和12.5%～81.08%，且处理时间可控。因此，针对大规模稀疏交通流量数据研究时，利用CFMC方法进行插补处理可进一步保障后续研究的准确性。