考虑电解槽和蓄电池寿命衰减特性的分布式电热氢系统优化调度策略

陈 杨，陈 健，张 文，倪筹帷，赵 波

（1.山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061；2.国网浙江省电力有限公司电力科学研究院，浙江 杭州 310014）

0 引言

大量具有随机性和波动性的可再生能源接入电网，给电网的安全稳定运行带来了挑战，如何高效利用可再生能源来减少弃风弃光是一个重要问题。分布式电热氢系统（distributed electric-thermo-hydrogen system，DETHS）作为一种灵活、高效的能源供应模式，集成了多种能源和转换设备，能够有效整合可再生能源和多元储能技术，实现可再生能源的高效利用和多元负荷供应，从而实现能量的梯级利用和系统的高效自治［1-6］。然而，DETHS 在运行中面临诸多问题，如可再生能源波动性导致的蓄电池［5］和电解槽［7］的寿命衰减加速等问题，因此，需要对这些问题进行深入研究，以提高系统的经济性以及延长设备寿命。

电解槽作为电氢耦合的核心设备，将电能转化为氢能，进而由储氢设备储存氢能。然而，电解槽在长时间运行过程中会受到输入功率波动的影响，从而导致其寿命衰减。目前，已有关于输入功率波动对电解槽寿命影响的研究，变功率运行与恒功率运行电解槽寿命衰减情况的对比结果显示，变功率运行的电解槽衰减更快，波动幅度更大，且频率越快，衰减越快［8-10］。文献［11］综述碱性电解槽和质子交换膜电解槽在波动性电源输入下的性能衰退机制和材料劣化机理；文献［12］提出一种电解槽阵列优化控制策略，将电解槽工作状态分为额定功率、波动功率和停机3 种状态，提升了电解槽阵列的综合寿命，但没有建立具体的电解槽寿命衰减模型；文献［13］考虑电解槽长时运行的效率衰减及其输入功率波动对电解槽耐久性的影响，建立电解槽全寿命周期成本模型；文献［14］建立一种考虑不同运行工况下电解槽的效率和寿命衰减模型，但没有考虑不同功率波动强度下的电解槽寿命衰减情况。

蓄电池作为储能设备，在DETHS 中起着削峰填谷的关键作用，其寿命直接影响到系统的能量存储和释放能力，对系统的经济性有重要影响。蓄电池的寿命衰减与其充放电过程中的充放电速率和荷电状态（state of charge，SOC）密切相关。充放电速率越快，则蓄电池的寿命衰减越快，放电深度越深，对其寿命影响越大［15-18］。文献［19］综合考虑蓄电池剩余容量、充放电功率及充放电次数对其寿命的影响，通过推导得出反映蓄电池每次放电损耗的数学模型；文献［20］将蓄电池寿命损耗带来的经济损失加入经济调度计算模型中，在提升系统经济性的同时延长了蓄电池寿命；文献［21］考虑蓄电池充放电深度和次数对其寿命的影响，利用加权吞吐量法建立蓄电池寿命评价模型，并在分布式电源的优化配置评价指标中考虑蓄电池寿命。

综上，现有文献已对蓄电池寿命衰减特性的建模和量化进行较多研究，但较少研究电解槽的寿命衰减特性及其建模和量化，且较少同时考虑电解槽和蓄电池的寿命衰减特性。电解槽的寿命衰减主要受电解槽功率波动和电解槽启停的影响，体现在效率的降低；蓄电池的寿命衰减受充放电深度、充放电频率等影响，体现在有效吞吐量的消耗。电解槽和蓄电池在DETHS 中均承担着促进可再生能源消纳的作用，电解槽的调度曲线可能会影响蓄电池的充放电行为，反之亦然，因此，有必要探索一种在提升DETHS 经济性的同时减少电解槽和蓄电池寿命衰减损耗的优化调度策略。

为此，本文对现有的电解槽寿命衰减模型进行改进，结合现有的蓄电池寿命衰减模型，将电解槽和蓄电池的寿命衰减统一量化到目标函数中，提出一种考虑电解槽和蓄电池寿命衰减特性的DETHS 优化调度策略，采用场景法处理可再生能源出力的不确定性，并且采用MATLAB 中的YALMIP 工具调用Gurobi 求解器进行仿真求解，验证所提优化调度策略能够在有效提升系统经济效益的同时减少电解槽和蓄电池的寿命损耗。

1 DETHS结构及设备建模

DETHS 可以实现系统内部多种能源供应，满足多类型负荷需求。本文研究的DETHS 包含能量供给、能量转换、能量储存和能量消耗4 个部分，其结构示意图如图1 所示。光伏和风机提供清洁电能，系统可通过向上级电网购电弥补系统内的能量短缺；以电解槽和燃料电池（本文采用质子交换膜电解槽和质子交换膜燃料电池）为主体的能量转换单元可以有效降低能源的梯级损耗，提高综合利用率；能量储存部分包含电储能、氢储能、热储能等多能储存设备，可以起到削峰填谷的作用。

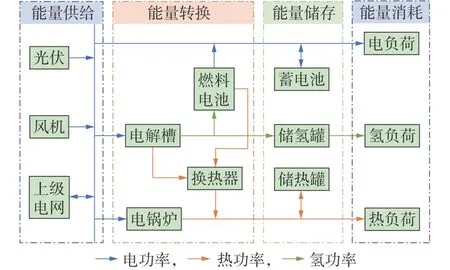
图1 DETHS结构示意图Fig.1 Schematic diagram of DETHS structure

1.1 电解槽数学模型

本文在文献［22-23］的基础上，根据电解槽的启动延时、启停能力、产氢和产热特性、工作范围、启动功率、爬坡能力、温度范围等特性参数建立电解槽模型。

1）电解槽启停模型。

考虑启动延时的电解槽启停特性的数学模型为：

式中：t为当前采样时段；T为采样时段总数；αEC为电解槽启动延时；分别为电解槽的开始启动动作和开始关停动作；U为0-1 变量，表示电解槽的开关状态；Δt为单位时间间隔分别为电解槽日内开机和停机次数上限。

2）电解槽产出模型，即：

式中：m为产出的氢气质量；分别为电解槽产氢和产热效率；P为电解槽工作功率；γ为1 kg氢气的热值等效系数；Q为电解槽产生的热功率。

3）电解槽功率模型。

电解槽工作功率上、下限约束分别为：

电解槽爬坡功率约束为：

式中：ΔP为电解槽在开机状态下的单位时段最大爬坡功率。

4）电解槽温度模型，即：

式中：T为电解槽温度；Q为电解槽损失的热功率为输出系统外的热功率；CEC为电解槽集总热容；T为电解槽外界温度；REC为电解槽热阻；分别为电解槽温度上、下限。

1.2 氢燃料电池模型

类似地，本文建立考虑氢燃料电池的启动延时、启停能力、产氢和产热特性、工作范围、启动功率、爬坡能力、温度范围等特性参数的氢燃料电池模型，具体如附录A式（A1）—（A14）所示。

常规设备如电锅炉、蓄电池、储氢罐、储热罐等的数学模型如附录A式（A15）—（A20）所示。

2 电解槽和蓄电池的寿命衰减模型

2.1 电解槽的寿命衰减特性及建模

电解槽的持续运行会导致电解槽寿命衰减，目前难以直接对电解槽的寿命衰减进行准确的数学建模，大多研究通过试验测量电解槽的电压变化间接反映寿命衰减情况，这是由于电解槽运行时催化层会产生不可逆损失，膜内阻变大，电解槽过电压增加，在保证输出氢气流速不变的条件下，需要保持电流不变，而工作电压上升表明电解槽制氢效率下降。当电解槽工作电压上升至最高工作电压时，为保证系统效率，需要更换电解槽，相关研究表明，在温度、压强等参数确定的情况下，电解槽电压变化与其功率波动情况关系密切。

电解槽平稳运行时会有一定的寿命衰减，在输入风、光等波动电源的情况下，电解槽输入功率的频繁波动以及电解槽的频繁启停会导致其寿命衰减加快。基于以上特性，本文参考文献［14］，用电解槽效率的衰减反映电解槽的寿命衰减，考虑平稳运行、波动运行和启停这3 种典型工况下的电解槽寿命衰减。在平稳运行时，电解槽的效率衰减系数很小；在波动运行时，波动越大，对应的效率衰减量也越大；启停对电解槽寿命的影响最大。

本文建立的电解槽寿命衰减模型为：

2.2 蓄电池的寿命衰减特性及建模

蓄电池的寿命损耗与SOC和充放电功率密不可分。文献［19］指出，蓄电池的寿命可表示为蓄电池可供使用的有效吞吐量之和，当累积的有效吞吐量达到蓄电池额定寿命时，需要更换电池。蓄电池的额定使用吞吐量为：

式中：GR为蓄电池的额定使用吞吐量；LR为蓄电池的额定循环寿命（额定放电深度和额定放电电流下的循环寿命）；DR为蓄电池的额定放电深度；CR为在额定放电电流下的蓄电池额定容量。

简化后的蓄电池寿命衰减模型为：

式中：St为t时段的蓄电池SOC；deff为使用一次蓄电池所消耗的吞吐量；k0、k1、k2为由蓄电池参数计算出的常数；u0、u1为仿真过程中测试得到的参数；dR为单次放电所消耗的额定吞吐量。

3 DETHS优化调度模型及求解步骤

3.1 源荷不确定性的处理

可再生能源和负荷均无法在日前准确预测，这导致电热氢系统源荷双侧均存在不确定性，给系统维持实时功率平衡和优化调度带来了挑战，因此，需要在制定调度方案时预先考虑不确定性的影响。本文采用场景法处理风、光出力和电、热、氢负荷需求的不确定性，场景法可以将具有不确定性的电、热、氢负荷和风、光预测结果转化为确定性的场景集，对每个典型场景进行调度，在调度方案中考虑不同的误差水平，并简化计算［24］。

3.2 DETHS多场景随机优化调度模型

3.2.1 目标函数

本文的优化目标是在提升各场景下电热氢系统经济性的同时提升电解槽和蓄电池的寿命，目标函数包含寿命损耗成本和运行净成本。

1）寿命损耗成本，即：

式中：Flife为寿命损耗成本；πκ为场景κ出现的概率；K为场景数；为在场景κ下电解槽寿命损耗成本为在场景κ下蓄电池寿命损耗成本和维护成本之和；为在场景κ下电解槽的寿命衰减量；分别为电解槽和蓄电池的配置成本为在场景κ下蓄电池消耗的有效吞吐量为蓄电池的单位维护成本分别为t时段在场景κ下蓄电池的充、放电功率。

2）运行净成本，即：

式中：Fop为运行净成本；分别为场景κ下的弃风弃光惩罚成本，切负荷惩罚成本，购、售电成本，碳排放惩罚成本和售热售氢收益；c为弃风和弃光惩罚系数分别为弃光和弃风功率分别为切电、热、氢负荷的惩罚系数；P为切电负荷功率；Q为切热负荷功率；m为切氢负荷质量分别为购、售电单价；分别为购、售电功率；ccar为碳排放的环境惩罚因数；ηele-car为电-碳转换系数分别为出售热功率和氢气的单价；分别为售出的热功率和氢气质量。

3.2.2 约束条件

调度中除了需满足各种设备的运行约束外，还需满足风机、光伏出力和负荷约束，购电功率约束以及电、热、氢能量平衡约束。

风机、光伏出力和负荷约束为：

购、售电功率约束为：

电功率平衡约束为：

热功率平衡约束为：

氢气质量平衡约束为：

3.3 求解步骤

考虑电解槽和蓄电池寿命衰减特性的DETHS优化调度模型以运行成本最低和寿命衰减最小为目标，以30 min 为单位采样时段，制定DETHS 的日前出力计划，模型求解流程图如图2所示。

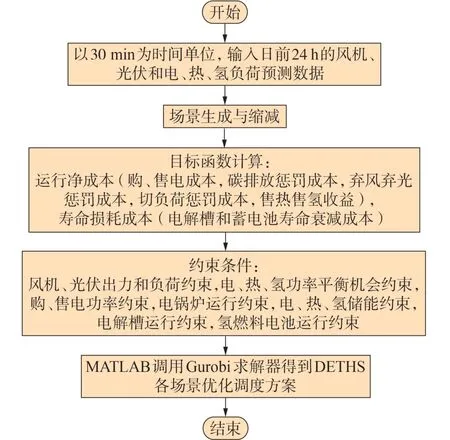
图2 模型求解流程图Fig.2 Solving flowchart of model

4 算例分析

4.1 算例概况

4.1.1 算例数据

以图1的DETHS为研究对象进行算例分析。电解槽和燃料电池参数见附录B 表B1，储能设备参数见附录B 表B2，分时购电价见附录B 表B3。售电价为购电价的80 %；电锅炉产热效率为0.9，日最大启停次数为4；电解槽成本为4 000元／kW，蓄电池成本为1 500元／（kW·h）；氢气售价为40元／kg，售热单价为0.5元／（kW·h）；电氢转换系数为33 kW·h／kg；蓄电池容量为1 000 kW·h，储氢罐容量为500 kg，储热罐容量为10 000 kW·h，电锅炉容量为1 000 kW。

4.1.2 源荷不确定性的处理

采用拉丁超立方采样生成1 000个场景，并通过改进的层次k-means算法进行场景削减，得到日前预测的5 个典型场景，如附录C 图C1 所示，场景1 — 5的概率分别为0.318、0.347、0.116、0.113、0.106。

4.2 算例结果分析

为分析考虑电解槽和蓄电池寿命衰减特性的合理性和有效性，本文设置4 个案例进行对比分析：案例1，不考虑电解槽和蓄电池的寿命损耗，目标函数为期望运行成本最低；案例2，不考虑电解槽的寿命损耗，目标函数为期望运行成本与蓄电池的寿命损耗成本之和最低；案例3，不考虑蓄电池的寿命损耗，目标函数为期望运行成本与电解槽的寿命损耗成本之和最低；案例4，综合考虑电解槽和蓄电池的寿命损耗，目标函数为期望运行成本与电解槽和蓄电池的寿命损耗成本之和最低。

优化结果如图3 所示，具体数据如附录B 表B4所示。

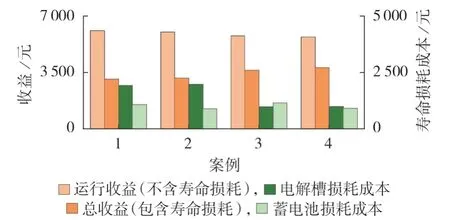
图3 不同案例的优化结果Fig.3 Optimization results of different cases

由图3 可知：案例1 不考虑设备寿命损耗成本，其运行收益最高，但该案例的调度方案导致的电解槽和蓄电池寿命损耗也最严重，在运行收益中减去寿命损耗成本后，总收益反而最低；案例2 的运行收益比案例1稍微降低，这是由于案例2考虑了蓄电池的寿命衰减成本，为了尽量降低蓄电池的寿命损耗，会牺牲一部分运行收益，但由于蓄电池成本相对较低，这对调度结果的影响不大；案例3 的运行收益比案例1降低幅度更大，这是由于案例3考虑了电解槽的寿命衰减成本，且电解槽的成本更高，电解槽的寿命损耗成本在总目标函数中的权重也会更大，因此该案例的调度方案会舍弃更多的运行收益以降低电解槽的寿命损耗；案例4 的运行收益最低，这是由于同时该案例考虑了蓄电池和电解槽的寿命损耗成本，但该案例的寿命损耗成本最低，系统综合收益最高。

1 000 个场景下案例1 和案例4 的各项成本和收益统计情况如附录C 图C2 所示。由图可知，相较于不考虑寿命衰减的情况，考虑寿命衰减时，为了减少电解槽和蓄电池的出力曲线波动，会增加购电量，从而增加了碳排放惩罚成本，这在大幅降低电解槽和蓄电池寿命损耗的同时也增加了售氢和售热收益，因此，案例4 的运行收益略低于案例1，但总收益却高于案例1。

为了进一步分析考虑电解槽和蓄电池寿命损耗对各设备调度方案的影响，以出现概率最高的典型场景2 为例进行分析，该场景下案例1 和案例4 的各设备调度结果如图4所示。

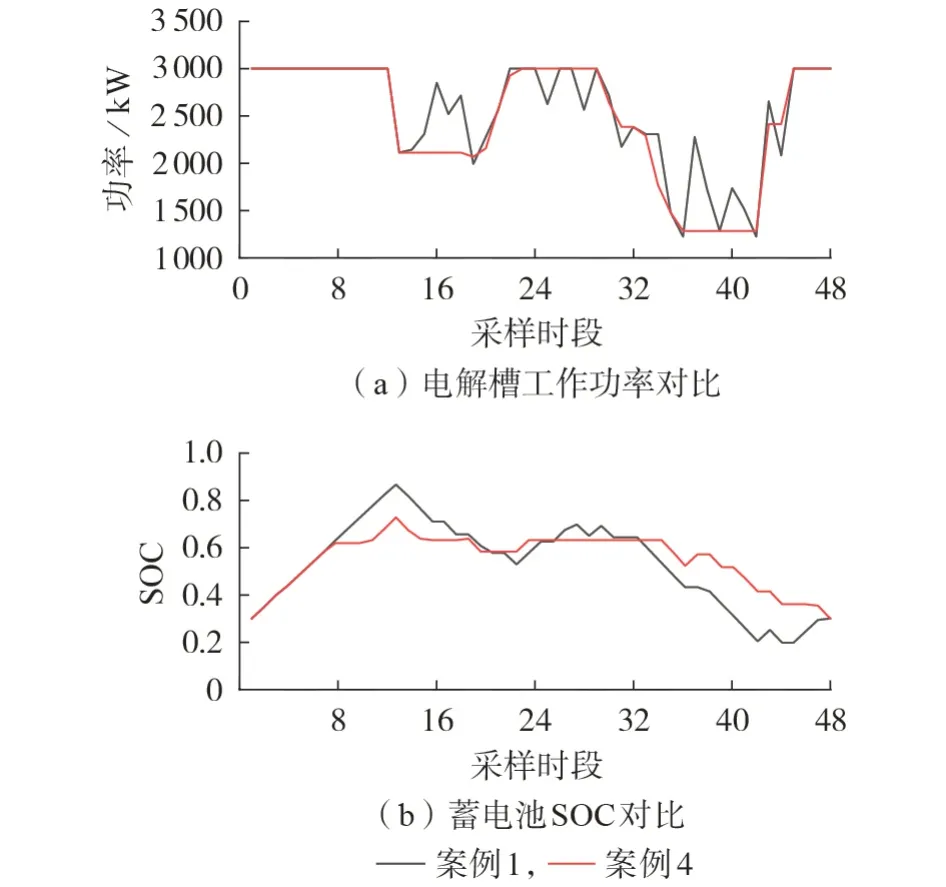
图4 电解槽和蓄电池的调度结果Fig.4 Scheduling results of electrolytic cell and battery

由图4可知：案例4的电解槽工作功率曲线比案例1 更平稳，波动更小，这是由于电解槽功率波动会加速其寿命衰减，为了降低电解槽寿命损耗成本，在案例4 的调度方案中会使用其他设备综合消纳可再生能源的波动，而不考虑寿命损耗成本的案例1 会优先使用电解槽消纳功率波动；案例4 的蓄电池SOC 在采样时段8 — 20 低于案例1，而在采样时段33 — 48 高于案例1，大多时候保持在0.6 左右，这是由于蓄电池的寿命衰减与SOC 水平相关，蓄电池的SOC 过高和过低均会使其寿命损耗增加，为了降低蓄电池的寿命损耗成本，会尽可能使蓄电池工作在合适的SOC下。

案例1 和案例4 的电功率平衡结果如附录C 图C3所示。由图可知：在案例4中，为了减少电解槽和蓄电池的出力曲线波动，会调节电锅炉的出力和购电功率，在风、光出力不足时从外部电网购电，在风、光出力过大时利用电锅炉将电能转化为热能供给热负荷；在案例1 中，为了降低运行成本，会通过直接快速调节电解槽的输入功率和充、放电平衡可再生能源的波动。

热功率和氢气质量平衡结果分别如附录C 图C4、C5 所示。由图可知，在案例4 中，在保证电解槽功率曲线更加平稳的同时，为了平衡热负荷的波动，增加了电锅炉、燃料电池以及储热罐的使用频率。

由于本文模型中电解槽和蓄电池的寿命损耗成本与其配置成本密切相关，且考虑到随着技术的成熟，电解槽和蓄电池的成本将会逐渐降低，为了体现电解槽和蓄电池配置成本变化对其出力曲线的影响，在案例4 中固定电解槽成本，改变蓄电池成本，蓄电池的SOC 曲线变化如图5 所示。蓄电池配置成本越高，则蓄电池寿命衰减成本在目标函数中的权重越大，蓄电池工作的SOC范围会越大，从而降低蓄电池寿命损耗成本。

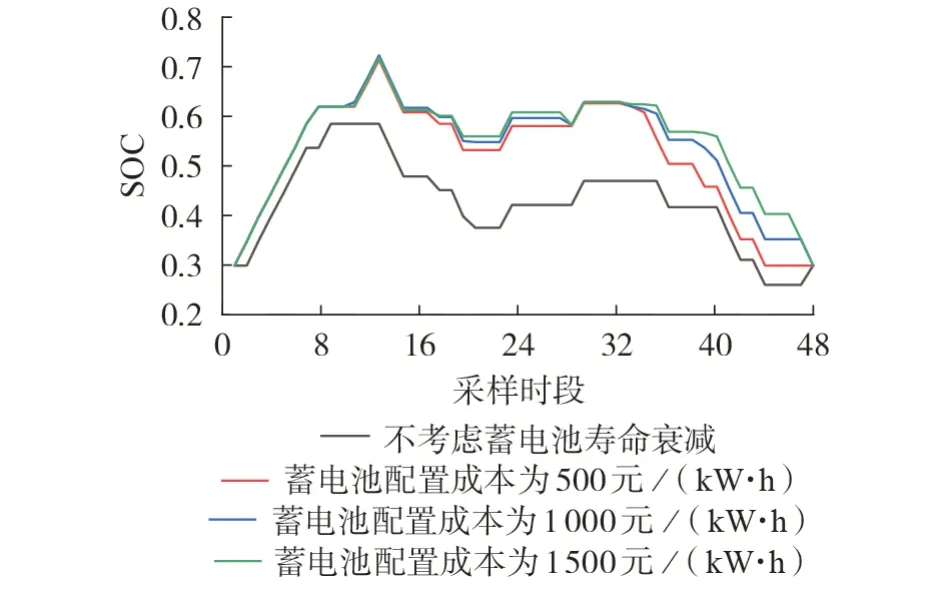
图5 SOC曲线与蓄电池配置成本的关系Fig.5 Relationship between SOC curve and allocation cost of battery

固定蓄电池配置成本，改变电解槽成本，电解槽的工作功率曲线变化如图6 所示。电解槽配置成本越高，则电解槽寿命衰减成本在目标函数中的权重越大，电解槽的工作功率曲线会越平稳，从而降低电解槽的寿命损耗成本。

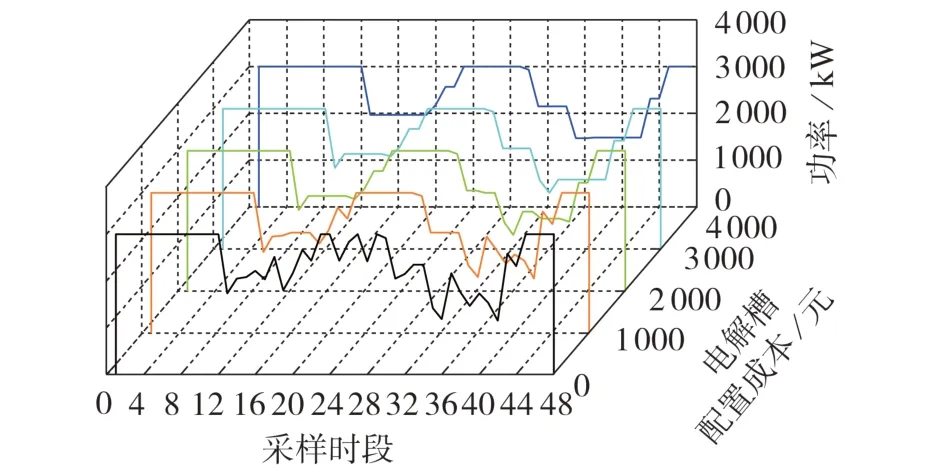
图6 电解槽出力曲线与配置成本的关系Fig.6 Relationship between output curve and allocation cost of electrolytic cell

由于售热和售氢价格变化也会对本文所提优化调度策略产生不可忽视的影响，因此，在不同的售热和售氢价格下进行优化调度，结果如附录C 图C6 所示。由图可知：在售热单价较低时，系统不会向外售热，而是在氢气价格较高时出售氢气，在氢气价格较低时将多余的电能向外出售，电解槽制氢供给氢负荷，存在部分功率波动，因此，电解槽寿命衰减较大，同时由于直接向外售电，蓄电池的使用频率较低，蓄电池的寿命衰减成本较低；随着售热单价的增加，系统开始向外售热，且在氢气价格较低时只向外售热，当氢气价格增加后同时向外售热和售氢，此时售电量急剧减少，电解槽寿命衰减成本逐渐降低，这是由于当售热和售氢价格增高后，系统通过从外部购电使电解槽高功率平稳运行，同时将电解槽产出的氢气和氧气向外出售，尤其在售氢和售热价格均最高时，系统大量购电，此时电解槽寿命衰减最小，而蓄电池更多地参与平抑电功率波动，从而使其寿命衰减增加。

5 结论

本文提出一种综合考虑电解槽和蓄电池寿命衰减特性的DETHS优化调度策略。通过对比分析4个案例下的系统运行收益、电解槽和蓄电池的寿命损耗成本及总收益，得出以下结论。

1）不考虑电解槽和蓄电池寿命损耗成本的调度方案能够获得最高的经济收益，但使电解槽和蓄电池的寿命损耗最严重。

2）在考虑电解槽和蓄电池寿命损耗成本的调度方案中，电解槽的工作功率曲线更平稳，蓄电池工作的SOC 在大多时候维持在合适水平，从而降低了设备寿命损耗成本，这使系统的经济收益略微降低，但使综合收益更高。

3）在考虑寿命损耗成本的情况下，售氢和售热单价对系统优化调度结果具有关键性的影响，售氢和售热单价较低时，蓄电池的寿命衰减成本较低，电解槽的寿命衰减成本较高，而售氢和售热价格较高时则相反。

为了制定更加准确的DETHS 优化调度方案，后续笔者将深入研究电解槽的效率变化特性，考虑电解槽温度对电解槽效率的影响，并将更加全面地考虑DETHS 中其他设备（如燃料电池、储氢罐等）的寿命衰减特性。

附录见本刊网络版（http：//www.epae.cn）。