三款弹性层状体系理论电算程序应用技术评析
李政贤 蒋 鑫 沙马伍呷 向嫣然 张 免
(1.西南交通大学土木工程学院 成都 610031;2.西南交通大学 道路工程四川省重点实验室 成都 610031;3.西南交通大学 高速铁路线路工程教育部重点实验室 成都 610031)
沥青路面具有表面平整、无接缝、行车舒适、耐磨、振动小、噪声低、施工期短、养护维修简便、适宜于分期修建等优点,因而得到了广泛的应用[1]。目前可应用于沥青路面结构力学分析的主要方法包括弹性层状体系理论、有限单元法(含轴对称有限元法、三维有限元法)、连续有限层法等[2],这些方法各有特点。在这些方法中,基于沥青路面各结构层水平层状分布之显著特征,弹性层状体系理论无疑是其中最为成熟、已被广泛采纳的经典理论。我国现行JTG D50-2017《公路沥青路面设计规范》[3]在开展沥青路面结构力学指标计算时即采用双圆均布垂直荷载作用下的弹性层状体系理论。
为解决弹性层状体系理论推导繁琐之弊端,随着数值计算、电子计算机等技术的发展,基于该理论所编制开发的电算程序纷纷涌现。比较具有代表性的程序包括由加州大学伯克利分校(University of California,Berkeley)开发的ELSYM5[4]、美国陆军工程兵团水道试验站(The Water-ways Experiment Station,US Army Corps of Engineers)开发的WESLEA,以及华盛顿州交通部(Washington State Department of Transportation)开发的EVERSTRESS[5]等。这些程序已获得一些应用,如文献[6]报道了ELSYM5程序与巴西国家公路局环形试验场地中传感器实测数据对比;文献[7]表明WESLEA程序可应用于评估路面的允许通过次数和允许的最大荷载;文献[8]则表明EVERSTRESS程序的疲劳和车辙计算结果与现场测量结果契合度较好。
但令人遗憾的是,迄今鲜有学者对这3款程序进行横向评析与深入挖掘,也未有人注意到这3款程序应用时可能存在的某些漏洞,这无疑大大增加了应用这些程序的风险性。本文尝试从结构层、荷载、计算点等方面出发,探讨以上3款基于弹性层状体系理论开发的沥青路面结构电算程序在开展轮载作用下附加应力计算时的差异,通过具体算例,经与解析解答比较,讨论WESLEA、EVERSTRESS这2款程序在处理结构层时的特点及缺陷,从而为这些电算程序的正确使用奠定坚实基础。
1 3款程序特点评析
1.1 结构层
ELSYM5程序可计算1~5层路面结构的力学响应,结构层自上而下由1开始连续依次予以编号。最下一层可为无限厚度的半无限体土基或有限厚度的土基。每一结构层均视为线弹性体,用弹性模量、泊松比来表征各结构层的材料性质。当最下一层为半无限体时,所有层间界面的结合状况只能视为完全连续;当最下一层为有限厚度时,其与上一结构层之间的层间界面结合状况可视为完全连续或完全光滑。
WESLEA程序可直接计算2~5层路面结构的力学响应,结构层亦按照从上至下由1开始的顺序依次编号。每一结构层均为线弹性体,需输入的材料参数为弹性模量、泊松比。层间结合状况可以考虑为完全连续或完全光滑。当输入的结构层数目<5时,最下一层无法直接考虑为半无限体,程序会在不改变用户已输入结构层的基础上自动将结构层数量添补至5层,添补的结构层全部位于用户所定义的最下一层之下,弹性模量、泊松比均与用户定义的最下一层保持一致,层间结合状况为完全连续。经添补所形成的第5层为半无限体,其余添补层厚度均为999 in或cm,以此达到考虑半无限体的目的。
EVERSTRESS程序可计算1~5层路面结构的力学响应,结构层编号方式为从上至下依次编号。每一结构层可为线弹性体、模量随体应力变化的粒料类材料或模量随偏应力变化的细粒土,其中若材料为线弹性体,则需输入的材料参数为弹性模量、泊松比;若为非线性弹性体,程序则使用式(1)、式(2)所示的幂指数模型分别来描述材料的动态回弹模量,此时需输入初始弹性模量、泊松比之外,还需输入式(1)和式(2)中所示的参数K1、K2或K3、K4。最下面一层土基固定为半无限体。层间接触关系可以考虑为完全连续、完全光滑或部分光滑。
Eb=K1θK2
(1)
(2)
式中:Eb为粒料类材料的动态回弹模量,MPa或ksi;Es为细粒土的动态回弹模量,MPa或ksi;θ为体应力,MPa或ksi;σd为偏应力,MPa或ksi;K1、K3为与含水率相关的回归常数;K2、K4为与材料类型有关的回归常数 。
1.2 荷载
3款程序均只能考虑圆形垂直均布荷载。为精准描述荷载作用位置,3款程序均引入空间直角坐标系。其中ELSYM5和EVERSTRESS两款程序限制坐标系的XY平面位于路表,Z方向竖直向下。WESLEA程序则稍有不同,由于其自带的荷载库(单轴双轮、双联轴、三联轴、单轴单轮)中轮距、轴距等几何参数已固定,为避免混淆,故无论是使用自定义荷载还是程序自带的荷载,程序均会对坐标系做出如下限制:XY平面位于路表,X方向为车轴方向,Y方向为行车方向,Z方向竖直向下。
ELSYM5程序可考虑1~10个大小、集度、半径均相同的圆形垂直均布荷载,无法考虑每个荷载的差异性。输入荷载力学参数时仅需输入荷载大小、集度、半径3个参数中的2个即可,程序会自动计算第3个参数。由于荷载作用于路表(XY平面),意味着荷载作用的Z坐标恒定为0,故输入荷载位置参数时仅需输入每个荷载圆心的XY坐标即可。
WESLEA程序内荷载分为两类,第一类是自带的荷载库,第二类是自定义荷载。其中自带的荷载库包括单轴双轮、双联轴、三联轴、单轴单轮4种类型。当使用自带的荷载库时 ,程序认为半轴的荷载对于另外半轴的路面结构影响甚小,可以忽略,故使用了对称性,仅需输入半轴的荷载,每种类型中荷载的位置参数已固定,见图1。自定义荷载的数目则限制在1~20个,但未限制荷载的位置。荷载力学参数仅有荷载大小和集度,无需输入半径。

图1 WESLEA程序自带荷载库的荷载圆心位置(单位:in)
EVERSTRESS程序可考虑1~20个大小、集度、半径互不相同的圆形垂直均布荷载,即可考虑每个荷载的差异性。此处应注意,根据作者多次尝试,EVERSTRESS程序似乎存在1个漏洞,荷载个数处无法输入“9”和“19”,若用户的确需要输入9个或19个荷载,那么可输入“10”或“20”,同时将其中一个荷载大小和集度均设为“0”。其余方面与ELSYM5程序相同。
1.3 计算点
3款程序均通过输入绝对坐标来确定计算点的位置。
ELSYM5程序至多可考虑10(XY坐标数)×10(Z坐标数)个计算点。确定计算点位置的参数为X、Y、Z坐标。计算点的位置信息输入方式为先输入计算点的X、Y坐标来确定计算点所在的纵剖面,再输入计算点所在的Z坐标来确定计算点所在的横剖面。这种输入方式的逻辑见图2,可以看出其本质上是X、Y坐标与Z坐标的排列组合,当需要计算的点为一层一层整齐排列的点时,这种输入方式可以极大提高输入效率。对于路表的计算点,Z坐标输入0即可。若输入的Z坐标刚好与结构层界面Z坐标相同,则程序会判定此计算点位于上一结构层的底部。
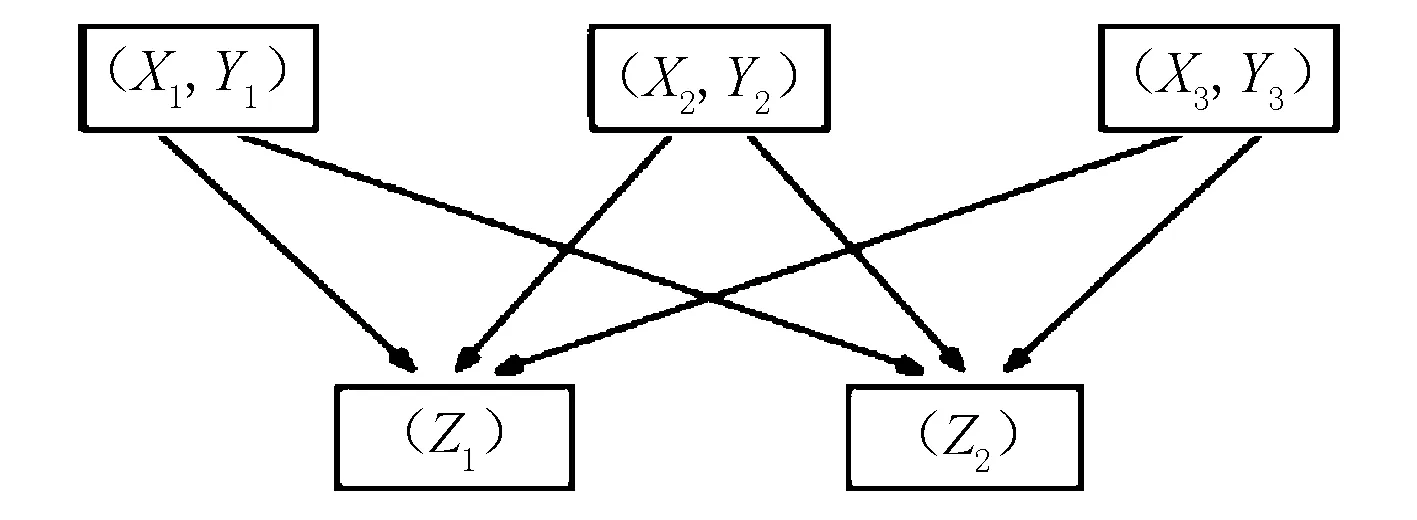
图2 ELSYM5程序计算点坐标输入逻辑
WESLEA程序至多可考虑50个计算点。确定计算点位置的参数为计算点所在的结构层号、X、Y、Z坐标。计算点位置信息需依次输入。对于路表的计算点,Z坐标输入0即可。若输入的Z坐标刚好与结构层界面Z坐标相同,则程序会根据计算点所在的结构层号判定此计算点是位于上一结构层的底部还是下一结构层的顶部。另外若使用的是自带的荷载库,则可选择使用程序所定义的标准计算点,标准计算点平面位置见图3,竖向位置有2个,分别为第一层底部和用户定义的最后一层顶部。
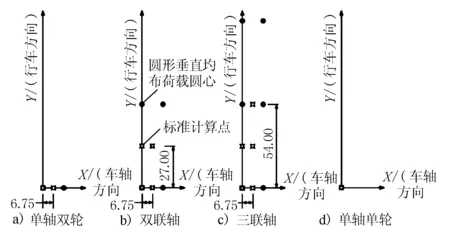
图3 WESLEA程序标准计算点平面位置(单位:in)
同时,对于WESLEA程序,若用户既选择了自带的荷载库,又使用了标准计算点,程序即可通过式(3)和式(4)计算路面达到疲劳破坏和车辙达到最大容许值时的荷载累计作用次数,计算图示见图4。之后按照式(5)计算损伤值。
(3)
(4)
(5)
式中:Nf、Nd分别为路面达到疲劳破坏和车辙达到最大容许值时的荷载累计作用次数;εt为第一层底部所有标准计算点的微拉应变的最大值;εv为用户定义的最后一层顶部所有标准计算点的微压应变的最大值;D为损伤值;N为荷载实际作用次数。
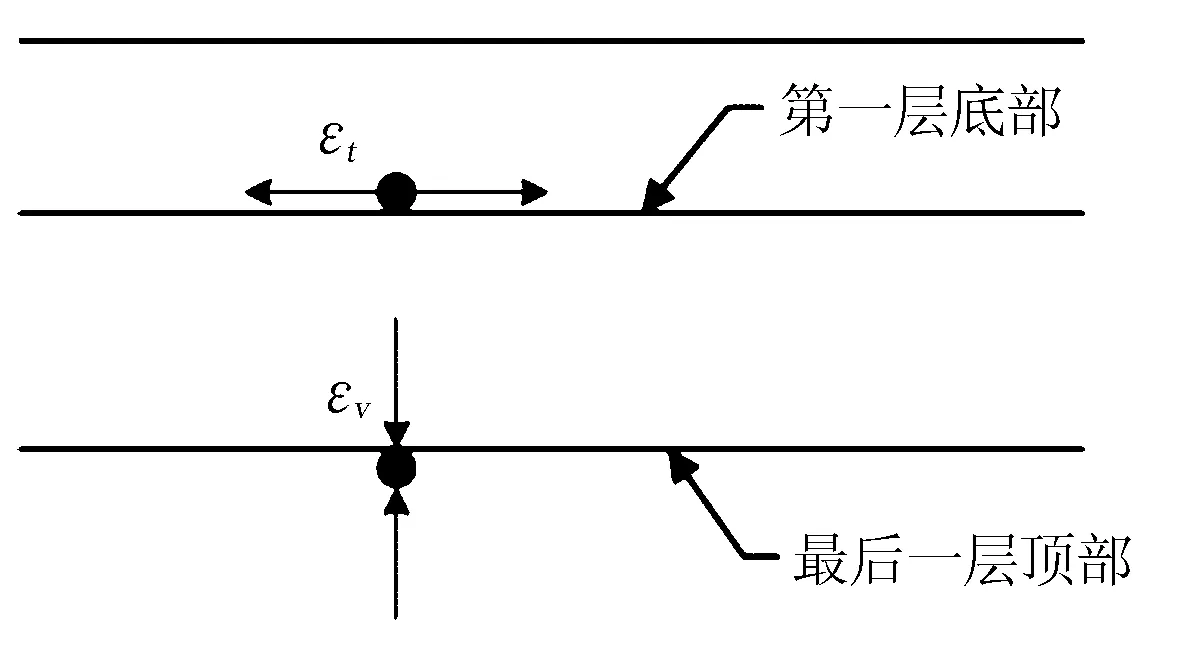
图4 WESLEA程序计算疲劳与车辙的计算点图示
EVERSTRESS程序至多可考虑50个计算点。确定计算点位置的参数为X、Y、Z坐标。计算点位置信息的输入方式与ELSYM5程序类似。对于路表的计算点,Z坐标输入0即可。若输入的Z坐标刚好与结构层界面Z坐标相同,则程序会判定此计算点位于上一结构层的底部。
3款程序针对前述计算点所输出结果的项目有所不同,具体列于表1。可以看出ELSYM5程序计算结果输出较为丰富,WESLEA程序的优势在于可以计算路面的疲劳和车辙寿命,而EVERSTRESS程序其特点在于可分析包含非线弹性体的路面结构的力学响应。
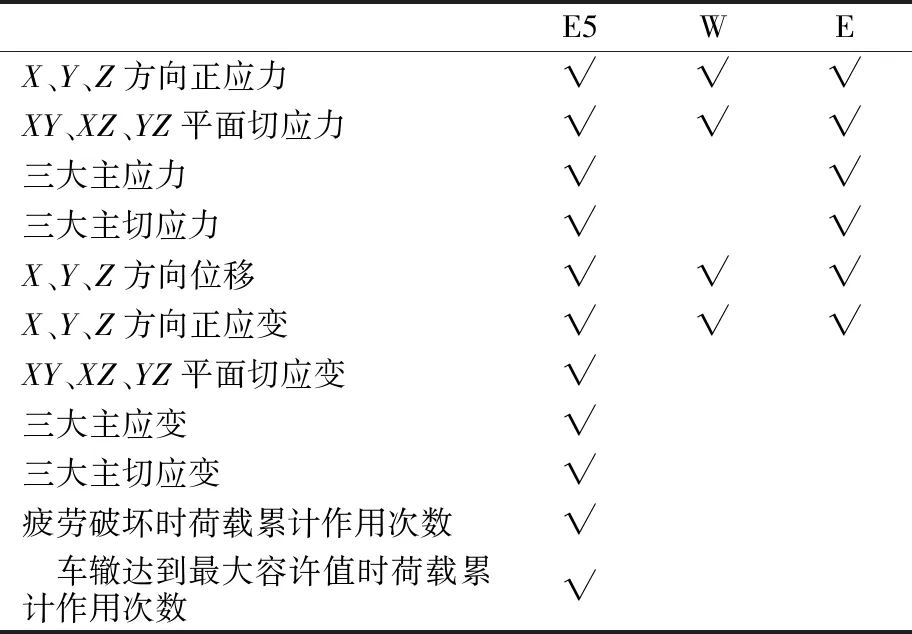
表1 3款程序输计算结果对比表
2 3款程序应用中存在的问题
2.1 WESLEA与EVERSTRESS两者共存的问题
虽然WESLEA与EVERSTRESS 2款程序在输入时可将路面结构拟定为5层,但是在作者实际使用过程中发现若将路面结构拟定为5层,则第5层结构中的计算点所有计算结果都将输出为0,这无疑是异常的,故有理由怀疑可能是程序设计方面存在缺陷。为验证此想法,此处以图5[9]所示算例为准,同时应用这3款程序分别视为2层、5层结构予以计算,并将结果与文献[9] 所提供的封闭解析解答对比。文献[9] 的计算公式如式(6)~(10)所示。
(6)
(7)
(8)
(9)
(10)
其中:σz为荷载中心竖向应力,psi;σr为荷载中心径向应力,psi;εz为荷载中心竖向应变;εr为荷载中心径向应变;w为荷载中心竖向位移,mm;q为荷载集度,psi;a为荷载作用半径,in;z为计算点深度,in;v为泊松比;E为弹性模量,psi。
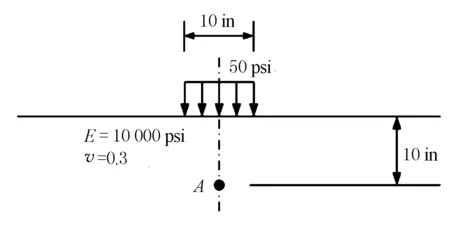
图5 路面结构
为验证前述想法,刻意将路面结构人为划分为2层、5层2种情况,层间接触均为完全连续,每层的弹性模量和泊松比均与图5中完全相同,并使A点均落在最下面一层结构中,划分后路面结构见图6。使用3款程序对这2种结构层输入方式分别予以计算,通过计算,表2列出了3款程序关于A点的竖向应力σz、径向应力σr、竖向应变εz、径向应变εr、挠度w等结果。文献[9]解析解答也一并列于表2中。需说明的是,各程序对正、负符号定义有所不同,只需关注计算结果绝对值即可。

图6 人为划分后的路面结构图

表2 计算结果汇总
可以看出,3款程序在人为地将路面结构划分为2层后的计算结果与解析公式算得的结果十分接近,证明此种划分方式是可行的。但是,WESLEA和EVERSTRESS 2款程序在人为地将路面结构划分为5层后的计算结果全为0。经作者多次验证,当同时满足以下2个条件时,3款程序均会出现此情况,即:路面结构层数达到上限,即5层,同时计算点位于第5层。故在实际使用中应特别注意3款程序的此项特性。
2.2 EVERSTRESS程序的特有问题
前文提到WESLEA程序会自动添补路面结构至5层,且可在其结果输出文件中轻易发现,以图6中输入的人为划分为2层的路面结构为例,其结果输出文件中关于结构层参数的内容见图7。其实经作者多次尝试后发现EVERSTRESS程序也有添补结构层至5层的特性,但在结果文件中体现得很不明显。其添补规则区别于WESLEA,具体规则如下:
若用户定义的路面结构总层数是X层时(X=2、3、4),程序在进行计算时会自动将结构补成5层,且自动补充层数后的路面结构有如下特点。
1) 程序自动补充的5-X层路面结构的厚度与用户自己定义的第X-1层结构相同。
2) 程序自动补充的5-X层路面结构的泊松比和弹性模量与用户自己定义的最下面一层结构(半无限体层)相同。
3) 第五层结构仍为半无限体层,与用户定义的半无限体层完全相同。
4) 自动生成的路面结构不影响用户定义的计算点位置。
5) 自动生成的路面结构不会显示在数据输入文件中,也不会直接显示在结果输出文件中,2个文件中显示的路面结构与用户输入的结构相同,但实际参与计算的是程序自动生成的路面结构。
用户自定义的路面结构与程序自动生成的路面结构对比见图8,可以看到其添补的实质就是在半无限体路基上额外增加若干结构层,这些结构层的弹性模量、泊松比与半无限体路基完全相同。

图8 EVERSTRESS程序结构层添补规则示意图
综合此特性和2.1节中提到的共性问题,使得在用户输入的路面结构小于5层的情况下仍可能出现计算点的力学响应仍全为0的错误,且由于自动生成的路面结构不会显示在数据输入文件中,也不会直接显示在结果输出文件中,使得此漏洞极难被发现。
为验证此结论,仍以前述图5所示算例为准,应用EVERSTRESS程序重新划分结构层再次予以计算,路面结构划分见图9。按前文所述,程序将会按照图8方式划分结构层,那么输入图9中1 in+9 in(9 in为半无限体层的一部分)所示的结构层将会被程序自动划分为1 in+1 in+1 in+1 in+6 in(6 in为半无限体层的一部分),则A点将会位于第5层中,A点的计算结果将全为0。同时除A点以外,此结构额外选取8个验证点,8个验证点的坐标列于表3。如此选定验证点坐标意在结合“程序的结果文件中会输出计算点所在的结构层号”这一特点验证每一层的厚度取值方式。

图9 验证EVERSTRESS时人为划分的路面结构图
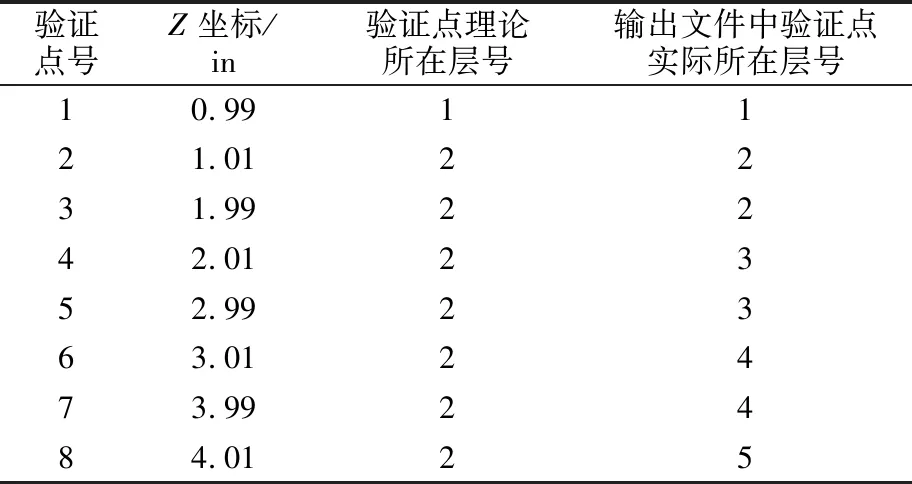
表3 8个验证点坐标及结果文件中显示其所在层号
EVERSTRESS程序结果文件中输入参数的部分见图10,可以看到其的确是用户输入的1 in+9 in(9 in为半无限体层的一部分)的路面结构。但是计算结果的部分截图见图11,统计结果后列于表3第4列。可以看到每个验证点所在的层号并非表3第3列所示,以此验证了EVERSTRESS程序对于结构层的添补规则。同时注意到A点(Z=10 in)的计算结果全为0,也与上一段相呼应。

图10 EVERSTRESS程序结果文件中部分输入参数
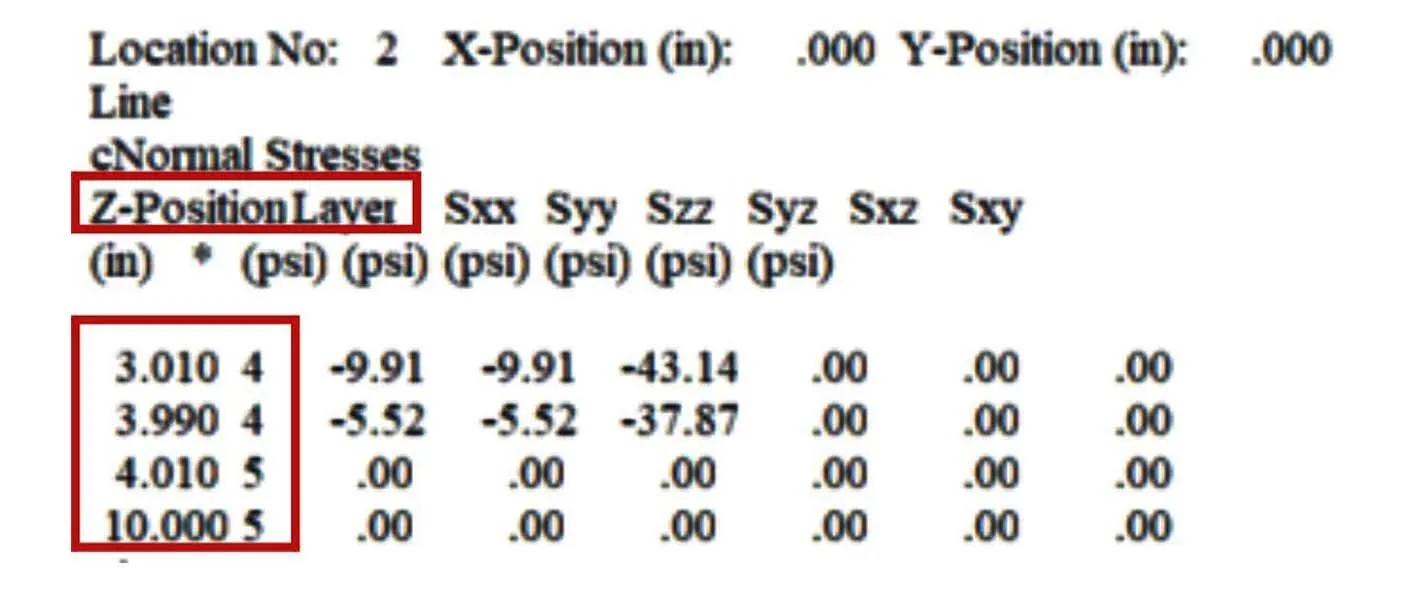
图11 EVERSTRESS程序结果文件中部分计算结果
综上所述,EVERSTRESS程序所存在的此缺陷较为隐蔽,不易发觉,使用该程序时应特别注意。
3 结语
3款程序均基于弹性层状体系理论开发,各有特色,在实际应用时需注意如下方面。
1) 若仅考虑较为基础的应用,则ELSYM5程序因其输出的力学响应最为全面而更具优势。但若需计算车辙及疲劳寿命,则仅可选用WESLEA程序;若需开展非线性弹性分析,则EVERSTRESS程序可胜任此工作。
2) WESLEA、EVERSTRESS这2款程序均无法正确计算5层路面结构情况下最下一结构层(即路基)的力学响应。
3) WESLEA和EVERSTRESS程序均存在程序自动添补结构层的情况,使用时应注意此特征,尤其是EVERSTRESS程序的添补行为很难发现,应予以特别关注。

