基于强化学习的大跨度桥梁风致振动主动控制研究
何佳琛
(中铁第四勘察设计院集团有限公司 武汉 430063)
主动控制措施依靠外部能源供给,可有效抑制大跨度桥梁的风致振动。主动控制律是主动控制设施的设计核心,其在很大程度上决定了主动控制设施的性能及鲁棒性。在结构振动控制领域中较常使用的主动控制律设计方法主要可分为传统控制算法和智能控制算法[1]。传统控制算法通过配置被控系统的极点或最小化既定的代价函数等方式来求解主动控制律。李珂等[2]利用线性二次最优控制算法为安装在桥梁甲板上方的主动小翼设计了自动控制方案,用于提高大跨度桥梁的颤振临界风速。文永奎[3]利用线性二次高斯控制算法为主动质量阻尼器系统(ATMD)设计了自动控制方案,成功抑制了斜拉桥施工阶段的抖振响应。传统最优控制算法虽有能力设计出名义上性能最优或者次优的控制系统,但在实施过程中需要测量结构的全状态信息,大跨度桥梁结构复杂,状态信息庞大,由传感器中大量信息传输而引起的时滞问题将大大影响控制系统的控制效果。
以神经网络和模糊理论为代表的智能控制算法在处理复杂性及不确定性方面有较高的能力。何敏等[4]提出了基于神经网络的大跨桥梁结构电磁驱动AMD系统输入电压的在线实时控制方法,用于降低结构的地震响应。颜桂云等[5]通过观测部分楼层加速度和控制力输出,建立了模糊神经网络控制器,大幅度降低了高层建筑的横风向振动,解决了传统控制中有限的传感器数目对系统振动状态估计的困难。以神经网络结构辨识和响应预测为前提的控制方案有着反应迅速及强鲁棒性等优点,但神经网络在训练过程中收敛较为困难,容易陷入局部最小值。模糊神经网络算法解决了传统模糊控制中专家知识难定义的问题,但却需要大量的高质量样本数据去训练算法中预先定义的神经网络,当样本数据难以获得时,其应用将受限制。
强化学习是人工智能的一个重要分支,其使用智能体与环境进行交互,并通过交互获得的反馈数据来找寻指定目标下的最优策略。强化学习在湍流的主动控制中已有颇多的研究成果[6],但到目前为止,还没有学者研究如何利用强化学习算法为风-桥系统设计主动控制律。本文主要探究基于强化学习的大跨度桥梁风致振动主动控制,以苏通长江大桥为背景,构建大跨度桥梁风致振动主动控制与强化学习框架各组分之间的对应关系,利用强化学习算法为主动质量阻尼器(active mass damper,ATMD)设计控制律,拟探究其对抖振的控制效果,并与利用线性二次型调节器所设计出的主动控制律在抑振效果层面进行对比分析。以检验利用强化学习算法所设计的控制系统在面对随机风环境及结构参数不确定时的鲁棒性能。
1 强化学习与桥梁风致振动的对应关系
在一个完全能观的环境中,强化学习任务通常假定满足马尔可夫决策过程(Markov decision process,MDP)。标准的马尔可夫决策过程可用四元组进行表示,即MPD=[S,A,p(st+1|st,at),r(st,at,st+1)],S和A分别为状态空间和动作空间;p(st+1|st,at)为在当前状态st下执行动作at后,环境转移到下一个状态st+1的概率分布;r(st,at,st+1)为在状态st下执行动作at后转移到状态st+1时所获得的奖励,其与环境特性相关并通常由专家指定。在强化学习任务中,智能体的目标是通过与环境进行交互,从而找寻到最大化期望累积奖励Eπ[R(τ)]的策略a=π(s|θ)[7]。大跨度桥梁风致振动主动控制与强化学习框架各组分之间的对应关系见图1。

图1 强化学习与大跨度桥梁风致振动主动控制对应关系
智能体代表着主动控制系统,环境代表着风-桥系统,在强化学习中,智能体试图找到最优策略π*(a|st)来最大化期望回报Eπ[R(τ)],在控制系统设计中,设计者期望找到最优控制律u=f(x)来最小化代价函数或性能指标J,因此,经过适当的改造如取相反数,代价函数可转变为奖励函数,此时最优控制律便等价于最优策略。此外,在控制系统设计中,控制系统通过用传感器采集系统响应信息来判断桥梁的动力行为,进而给出实时控制信号u。在强化学习中,智能体通过观测环境的状态s来了解环境内部的演变,进而做出下一步动作a。因此,环境的状态s与系统响应信息是对应的,控制信号u与动作a是相对应的。
2 基于主动质量阻尼器的大跨桥梁抖振控制
苏通长江公路大桥是主跨为1 088 m的双塔双索面斜拉桥,利用ANSYS建立其空间有限元模型,动力分析结果表明,其第一阶横弯、竖弯,以及扭转模态对应的频率分别为0.100 7,0.188 0,0.529 8 Hz。在风荷载作用下,安装主动质量阻尼器的桥梁,其运动方程为
(1)

kei[qei(t)-qsi(t)]-uei(t)
(2)

将式(2)代入式(1),并化为简洁形式。
(3)
式中:
假定在苏通大桥主跨1/3截面处对称布置2个100 t的ATMD,选择桥梁的一阶对称竖弯频率作为主控频率,ATMD的频率比和阻尼比分别设为0.99和0.061,作动器提供的最大控制力取为1 000 kN。根据上述理论,利用newmark-β法求解结构响应,在不施加控制力ue的情况下(此时ATMD退化为调谐质量阻尼器TMD),桥梁跨中的位移和加速度响应时程见图2,位移峰值和均方根值(root mean square,RMS)分别为1.305和0.383 m,加速度峰值和均方根值分别为2.705和0.647 m/s2。
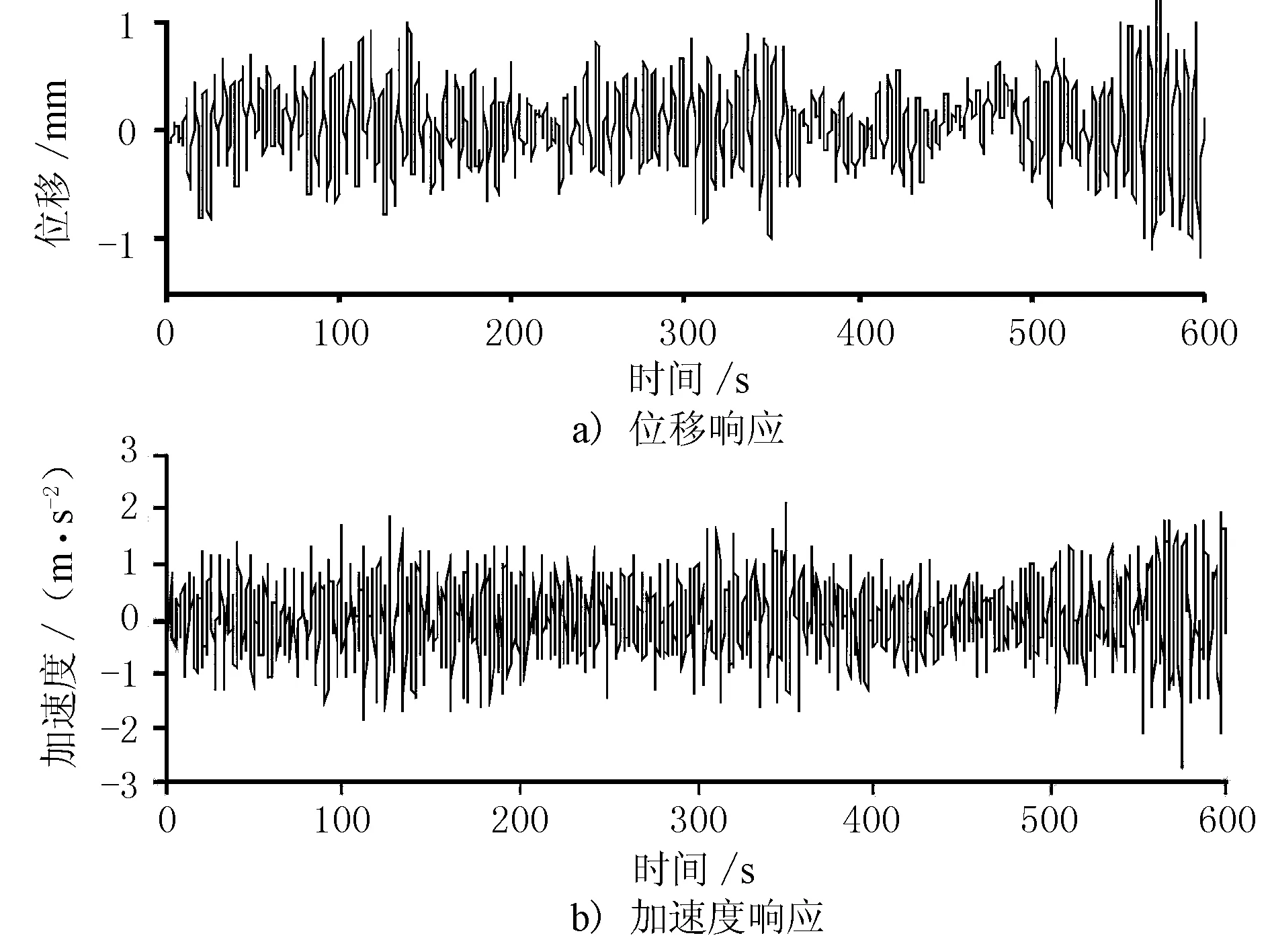
图2 不施加控制力时桥梁跨中的位移和加速度响应时程
3 基于强化学习的ATMD主动控制律求解
3.1 算法配置与训练过程
深度确定性策略梯度强化学习算法[8](deep deterministic policy gradient,DDPG)采用神经网络建模策略函数a=π(s|θπ)和状态-动作值函数Q(s,a|θQ),并引用深度Q网络算法中的经验回放机制和目标网络机制进一步稳定学习过程,加快收敛。在学习过程中,智能体与环境进行交互并将交互得到的状态-动作-下一状态-回报值(st,at,rt,st+1)存入经验回放池,随机抽取P个经验样本,最小化根据最优贝尔曼方程计算出的损失函数L来更新状态-动作值函数Q(s,a|θQ)。
Q(si,ai|θQ)}2
(4)
式中:Q*(·)为目标Q网络;π*(·)为目标策略网络;θQ*和θπ*为相应的模型参数。策略函数π(s|θπ)根据策略梯度θπJ进行更新。
(5)
基于DDPG算法的ATMD主动控制律求解步骤见表1。

表1 基于DDPG算法的ATMD主动控制律求解步骤
3.2 算法配置与训练过程
选择桥梁跨中节点的竖向加速度响应和竖向位移响应作为描述风-桥系统的状态变量s,将作动器所提供的控制力ue选为动作a,将系统的奖励函数ri设置为如式(6)形式。
(6)
式中:系数a和b分别为位移和加速度相应的惩罚项,即位移和加速度越大,智能体单步所获得的奖励将越小,为获得较大的总期望回报,智能体必须找寻到尽可能降低位移和加速度的策略,这与减振的目标一致;正常数c可以看作是奖励函数的偏置,其保证单步奖励值处于一个合理的范围,有助于防止梯度消失现象,加快网络收敛,本文采用试错法将系数a、b和c的值最终定为1,1和0.8。智能体由策略神经网络和状态-动作值神经网络组成,两者均采用如图3所示的4层神经网络,隐藏层内神经元个数均设为10个,W1~Wn为神经网络的权重系数;b为神经网络的偏置。策略神经网络和状态-动作值神经网络的学习率分别设置为0.005和0.001,软更新因子和折扣因子分别设置为0.01和0.99,网络训练时终止时间步取为600 s,经验回放池大小设置为20 000,当回放池数据储存量达到上限之后,先进入的数据将会被后进入的数据替代,即新的经验知识会代替旧的经验知识。采用python语言及开源机器学习框架Tensorflow可编制计算程序,训练过程见图4,共训练了M=1 142个回合,奖励值最终稳定在1 800附近。
3.3 评价指标与控制效果
定义ATMD控制效果评价指标如式(7)~(11)。
(7)
(8)
(9)
(10)
(11)

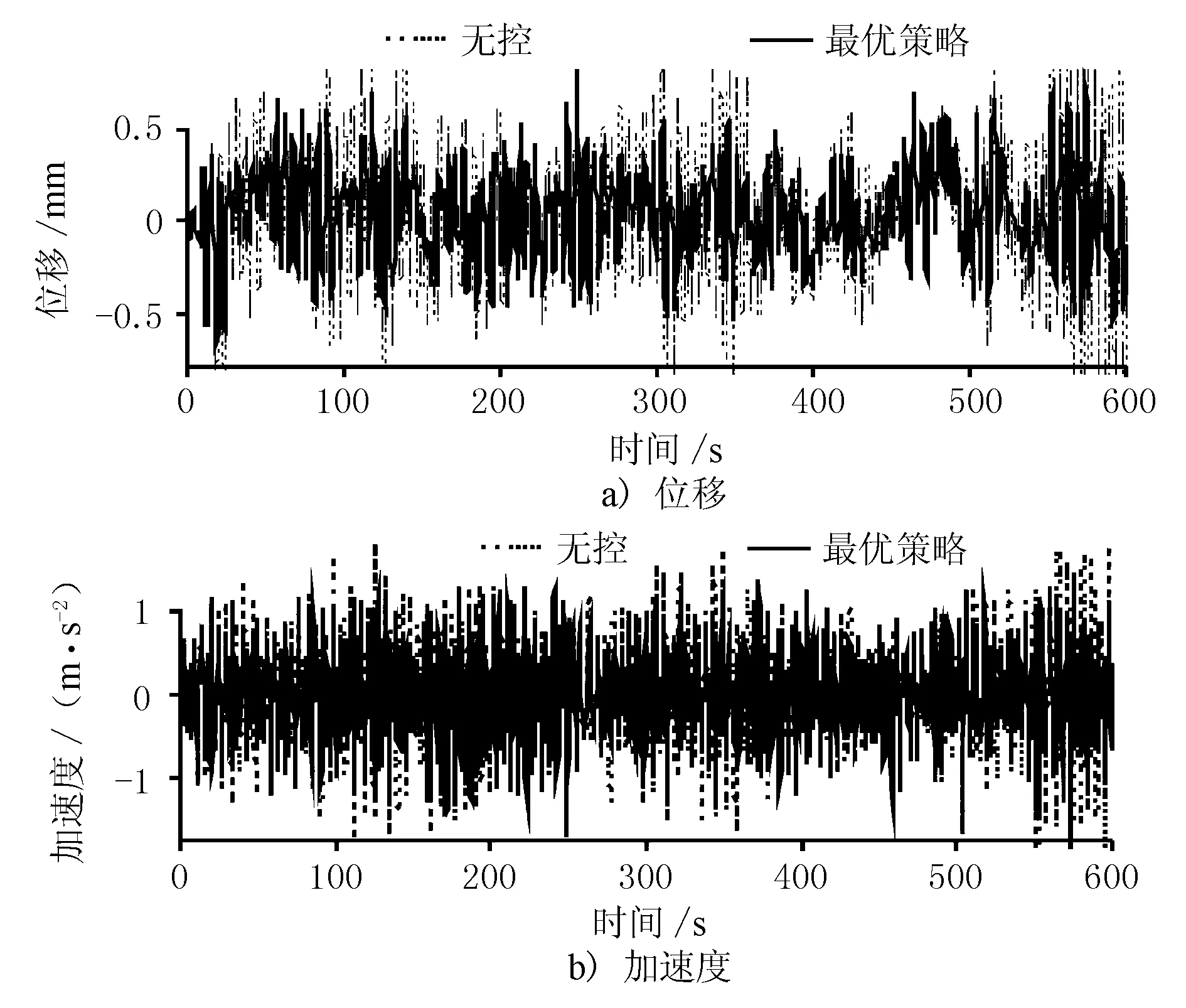
图5 基于深度确定性策略梯度算法的大跨度桥梁抖振控制效果(跨中节点)
表2对基于DDPG算法和LQR算法的大跨度桥梁抖振控制效果进行了对比,结果显示,利用强化学习算法为风-桥系统设计的主动控制系统可达到与LQR算法相当的减振效果,均接近30%。但是利用DDPG算法设计出的主动控制律在实施时仅需要测量桥梁跨中节点的位移响应和加速度响应,而不需要获取结构的全状态信息,可有效避免时滞效应,可实践性强。
4 控制系统鲁棒性检验
控制系统的鲁棒性是指系统在不确定性的扰动下,具有保持其性能不变的能力。为探究利用强化学习所设计的ATMD的鲁棒性,本文共设计了6个工况,工况1和工况2采用谐波合成法重新生成2条和训练时不同的脉动风速样本,检验在随机风环境下ATMD的工作情况。工况3~6分别考虑桥梁总体刚度退化10%、退化15%、提高10%,以及提高15%时所设计的ATMD的性能。表3给出了不同工况下利用DDPG算法所设计的ATMD的减振效果。不同工况下利用DDPG算法设计的ATMD的减振率见图7。

表3 不同工况下利用DDPG算法所设计的ATMD的减振效果
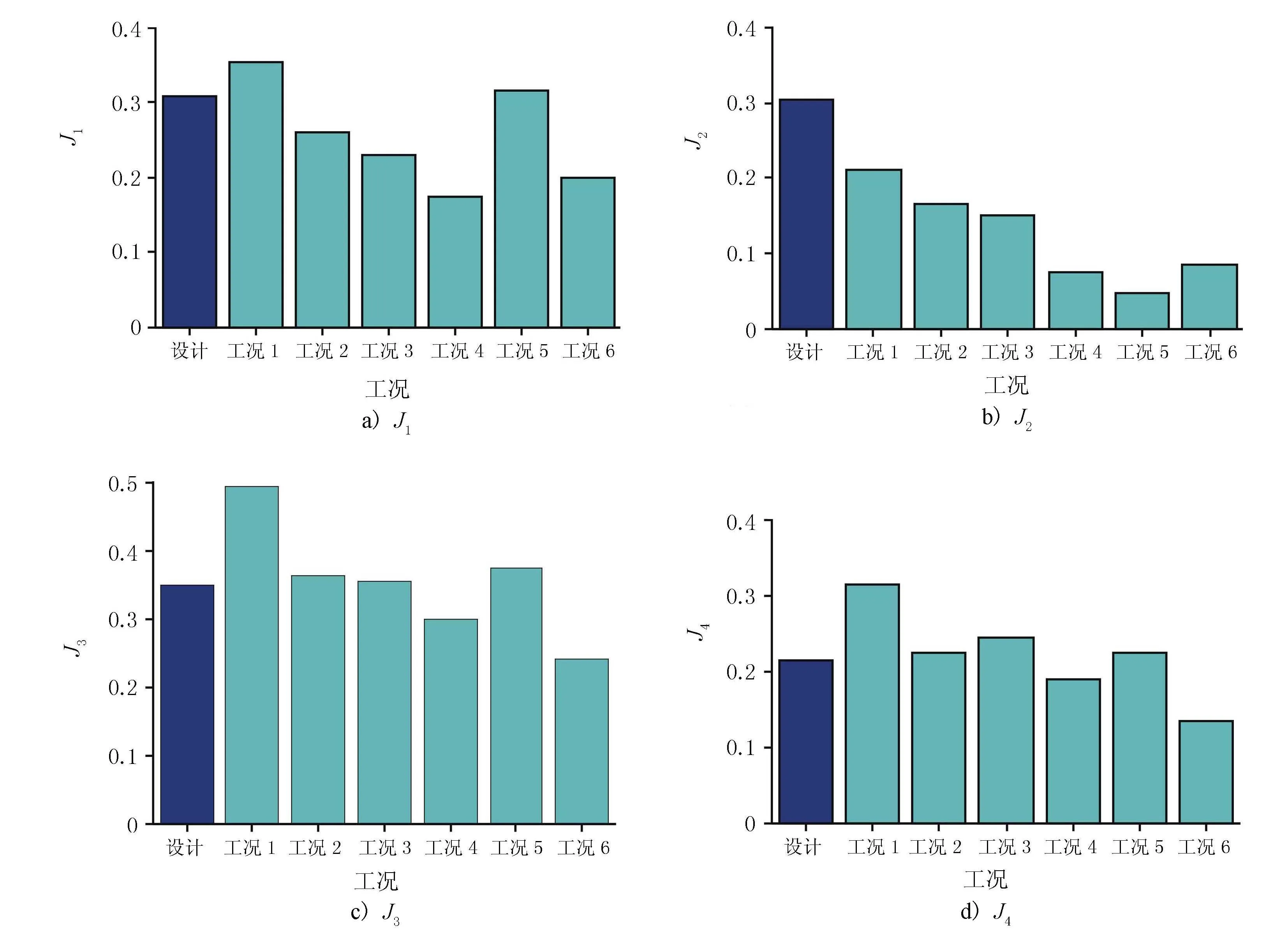
图7 不同工况下利用DDPG算法设计的ATMD的减振率
结果表明,当系统产生外部扰动即紊流风环境发生改变时,利用强化学习设计的ATMD仍然具备优越的控制性能。而当桥梁结构本身的刚度矩阵发生改变时,ATMD的减振性能虽有所衰退,但仍然能有效地降低桥梁结构的风致振动。此外,就单个工况而言,在大多数情况下,均方值控制效果总是优于相应的峰值控制效果,这种现象可能与强化学习的理念有关。强化学习中智能体的目的是找寻到最优策略最大化总期望回报,而非最大化单步奖励,因此,智能体在寻找最优策略的过程中,具有较为长远的“眼光”,即为了在之后可以获得较大的期望回报,并不会拒绝过程中出现的相对较小的单步奖励。在控制器设计中,这种学习理念可能会导致控制器弱化对响应峰值的削减,而是从整体的角度,专注于降低响应的均方差值。
5 基于强化学习的非线性涡振主动控制
为进一步说明强化学习的通用性,探究其对非线性系统的控制能力,本小节以宽高比为4的矩形断面为基础,研究了强化学习对非线性涡激振动的控制效果。所采用的矩形断面宽度和高度分别为300,75 mm;线质量为6.085 kg/m;竖向振动频率为13.43 Hz;质量比和阻尼比为0.001 1和0.002 1;Scruton数和Strouhal数为6.0和0.136;气动参数Y1、Y2、ε分别为6.27,-5.7,1 082.2。考虑在桥梁节段上施加1个理想的控制力u,则桥梁-理想控制器耦合系统可用以下方程(12)进行描述。
(12)

图8 控制前、后无量纲化的量涡振响应时程
6 结论
1) 利用强化学习算法为风-桥系统设计的主动控制律可达到与LQR算法相当的减振效果。但利用DDPG算法所设计出的主动控制系统在实施时仅需要测量桥梁跨中节点的位移响应和加速度响应,而不需要获取结构的全状态信息,可有效避免时滞效应,可实践性强。
2) 当系统产生外部扰动即紊流风环境发生改变时,利用强化学习设计的ATMD仍具备优越的控制性能。而当桥梁结构本身的刚度矩阵发生改变时,ATMD的减振性能虽有所衰退,但仍然能有效地降低桥梁结构的风致振动。
3) 强化学习是一个适用范围广泛的通用性框架,可用于线性或非线性系统。但由于在强化学习的理念中,智能体的目的是找寻到最优策略最大化总期望回报,而非最大化单步奖励,因此利用强化学习所设计的主动控制系统,其均方值控制效果会优于相应的峰值控制效果。

