基于运动波方程的道面水膜厚度动态演变研究
黄琴龙 吴鸣涛 蔡爵威
(1.同济大学道路与交通工程教育部重点实验室 上海 201804; 2.上海市建筑科学研究院有限公司 上海 201108)
道面湿滑严重影响飞机的制动能力和转弯性能,极易造成飞机“漂滑”现象[1],对飞机起降的安全性构成极大威胁。由于飞机滑跑速度高,机场道面抗滑性能对水膜厚度的变化非常敏感,有效获取道面水膜厚度的动态演变信息,有助于识别与预警湿滑状态下飞机滑跑安全风险,是机场安全运营工作和“四型机场”建设的重要内容。
近年来,国内外许多学者通过理论推导和试验数据拟合等手段,对道面水膜厚度分布开展研究。张理等[2]采用谢才公式和曼宁公式进行理论推导,得到了不同降雨强度和道路横纵坡条件下的水膜厚度公式。李光元等[3]采用极差分析法得到水膜厚度影响因素的主次顺序,回归分析了人工降雨试验数据,得到了水泥混凝土道面的水膜厚度预测模型。尚彦宇等[4]通过零纵坡轴推导了路面径流特征,建立了超高渐变段路面模型。总体而言,上述模型适用于降雨强度稳定不变的情况,但无法实时、动态求解道面水膜厚度。
本文基于运动波方程和水力学基础理论,拟结合道面纹理,横、纵坡排水,以及实时降雨强度,提出道面水膜厚度求解的基本控制方程;采用Preissmann法和MacCormack法对模型进行动态求解,并在恒定降雨强度和变化降雨强度2种条件下进行模型验证。
1 模型构建
道面水膜厚度的动态演变,可采用一维模型和二维模型进行计算。二维模型采用有限元方法,精细化模拟道面的真实纹理状态和水流的运动,从而精确求解道面水膜厚度,但计算耗费时间较长、概化困难,且需要高分辨率高程数据进行支撑,二维模型过大的计算量会极大增加系统负担。而一维模型根据道面高程数据和计算网格密度,提取道面内水流流线,并计算各流线上水膜厚度;通过各流线的汇流关系,计算道面各网格的水膜厚度值,最终获取道面水膜厚度的动态演变,具有计算效率高、计算时间短、所需边界信息及高程数据较少等优点[5]。因此本研究采用一维模型对道面水膜厚度的动态演变进行求解。
1.1 道面径流流线提取
为了获取道面水膜厚度动态演变,首先需要确定道面径流的流线。在网格单元划分的基础上,假定网格单元内最大坡降方向与坡度均为定值,区域内最大坡降方向即为流线方向,由此可计算出网格边界任意点起始的流线轨迹。对于不同网格间流线轨迹的衔接,上游网格单元内的流线终点即为下游网格单元内的流线起点,由此可将流线从跑道中线逐步推算到道肩。
通过对网格进行编号(Xj,Yk)确定单元及其对应位置,提取道面的流线,网格间流线组合示意图见图1。
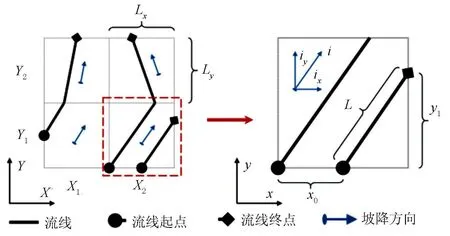
图1 道面网格划分与网格间组合流线示意图
流线与坡降方向平行,对于流线经过的任意网格,起点不同的流线不会相交;对于任意起点在单元内的流线终点,均可以通过其在单元内的位置和坡降方向信息计算得到,并代入下一单元内继续计算。
在任意网格单元(Xj,Yk)内,流线起点位置为(x0,y0),流线终点位置为(x1,y1)。当流线起点在x方向时(即x0≥0,y0=0),对于不同起点和坡度的网格单元,流线终点可能在坡降方向所指向的2条边界(即y方向边界、x方向边界)及其交点(x方向边界和y方向边界的交点)处,其所对应下一个单元的网格编号分别为(Xj+1,Yk)、(Xj,Yk+1)、(Xj+1,Yk+1)。图1右侧图为流线起点在x方向时的示意图,计算方法如式(1)所示。
(1)
式中:LX为网格单元在x方向的长度,m;LY为网格单元在y方向的长度,m;i为网格单元内的综合坡度,%;ix为网格单元内x方向的坡度,%;iy为网格单元内y方向的坡度,%。
当流线起点在y方向时(即x0=0,y0>0),只需将式(1)中的x与y、X与Y互换即可。
1.2 道面水膜厚度控制方程
水泥混凝土道面径流可视为坡面流的汇流过程,可采用一维圣维南方程进行表征,其基本方程包括连续方程和动力方程,分别如式(2)、式(3)所示。
(2)
(3)
式中:t为时间;q为降雨强度;x为距道面径流某固定断面沿流程的距离;h、u、Q分别为x处过水断面的水深(即水膜厚度)、断面平均流速、断面平均流量;g为重力加速度;S0、Sf分别为坡底源项和摩擦源项。
式(2)是连续方程,第一项为沿程流量的变化率,第二项为蓄量的变化率,第三项为降雨强度,反映了流线中的水量平衡;式(3)是动力方程,第一项为局部加速度项,第二项为对流加速度项,第三项为压力梯度项,第四项为水流内部及边界的摩阻损失,反映了水流克服压力和摩阻引起的能量损失而获得加速度。
道面径流属于地表漫流,可将其流动视为运动波,因此可以忽略动力方程中的局部加速度项、对流加速度项、压力梯度项,将式(3)调整为式(4)。
g(Sf-S0)=0
(4)
曼宁公式作为一种经验公式,常用于明渠流水力计算。道面上薄层水流状态是紊流,具有自由表面,且重力是其流动的主导因素,因此将曼宁公式带入谢才公式,可获得流速u与糙率n、水力坡度J,以及水力半径R的关系,如式(5)所示。
(5)
式中:水力半径R为过水断面面积A与湿周C的比值,其值约等于水膜厚度h,即R=A/C≈h;水力坡度J为比降,即道面横坡i,即J=i。代入式(5)可得式(6)。
(6)
式(6)两边同乘h,得到流量Q与水膜厚度h、糙率n及道面横坡i的关系,如式(7)所示。
(7)
由于道面横坡i足够小,tani近似与i相等。因此将式(7)调整为式(8)。
(8)
式中:m= 5/3;α= (tani)1/2/n;MH/T 5036-2017 《民用机场排水设计规范》中给出的沥青混凝土或水泥混凝土道面的糙率为0.013,取n=0.013。
联立式(8)与式(2),得到道面水膜厚度求解的基本控制方程,如式(9)所示。
(9)
2 模型求解
采用Preissmann四点隐式差分法和MacCormack差分法,将式(9)在时间和空间2个维度上,进行离散化并求解。
2.1 Preissmann四点隐式差分法
对于函数f(x,t),按式(10)计算各因变量对其导数的离散形式。
(10)
式中:θ为加权系数,0 <θ≤1。
将式(10)带入式(9)可得
(11)
2.2 MacCormack差分法
MacCormack差分法按照预测-修正的方式,对式(9)进行求解。预测步、修正步分别如式(12)、式(13)所示。
(12)
(13)
2.3 边界条件
在求解过程中,取未降雨(或刚开始降雨)的时刻为 0 时刻,且流线起点为道面高程的极大值点,整个模型的边界条件满足式(14)。
(14)
3 模型验证
3.1 恒定降雨强度下水膜厚度计算
季天剑等[6]选取了AC-25、AC-20和SMA-13 3种典型道面结构,开展了道面水膜厚度试验,建立了计算水膜厚度的回归方程。本文参考其试验条件,将其试验数据作为实测值,对比分析本文模型的水膜厚度计算值,结果见图2。
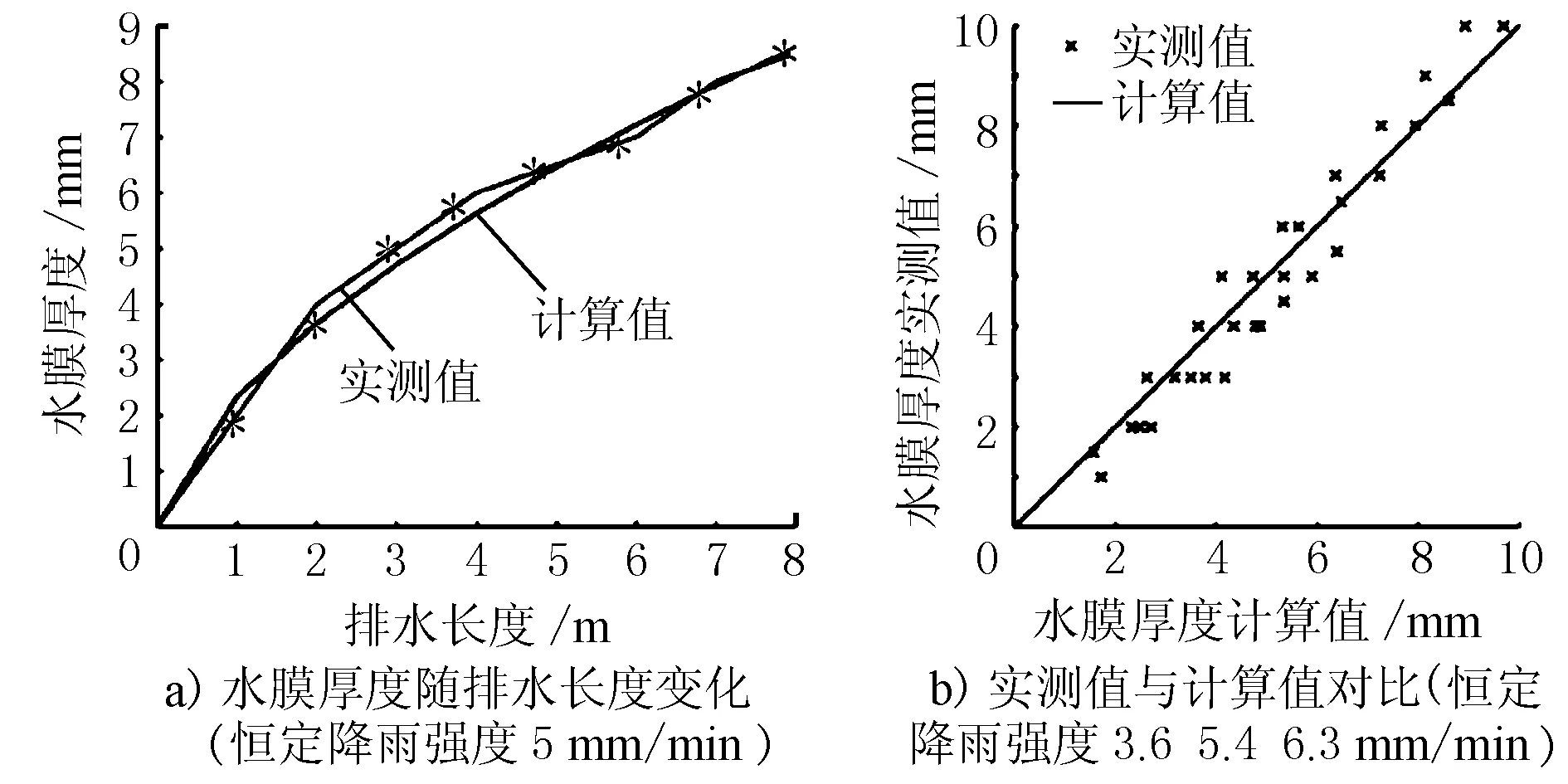
图2 SMA-13改进型路面结构实测值与计算值对比
图2a)选取恒定降雨强度5.4 mm/min,排水长度0~8 m共9种工况,对水膜厚度实测值与计算值进行比较,可以看出,在不同排水长度下,水膜厚度的计算值与实测值吻合度较高。图2b)选取恒定降雨强度3.6,5.4,6.3 mm/min,排水长度0~8 m共27种工况,对水膜厚度实测值与计算值进行比较,可以看出,在不同排水长度、不同降雨强度下,水膜厚度的计算值与实测值仍保持较高吻合度,两者的平均绝对误差为0.54 mm,平均精度为85.1%。考虑到文献[6]中水膜厚度测量分辨率为0.5 mm,因此可以认为,在恒定降雨强度下,本文提出的计算模型具有较高精度。
3.2 变化降雨强度下水膜厚度计算
采用本文提出的模型,计算变化降雨强度及坡度情况下的水膜厚度演变情况。随机生成30 min的降雨强度序列,计算结果见图3。由图3可见,水膜厚度演变情况与降雨强度变化呈现出较好的一致性,模型很好地反映了在降雨强度改变时水膜厚度的演变情况,以及降雨停止后积水的消散,避免了回归模型中的结果突变现象。
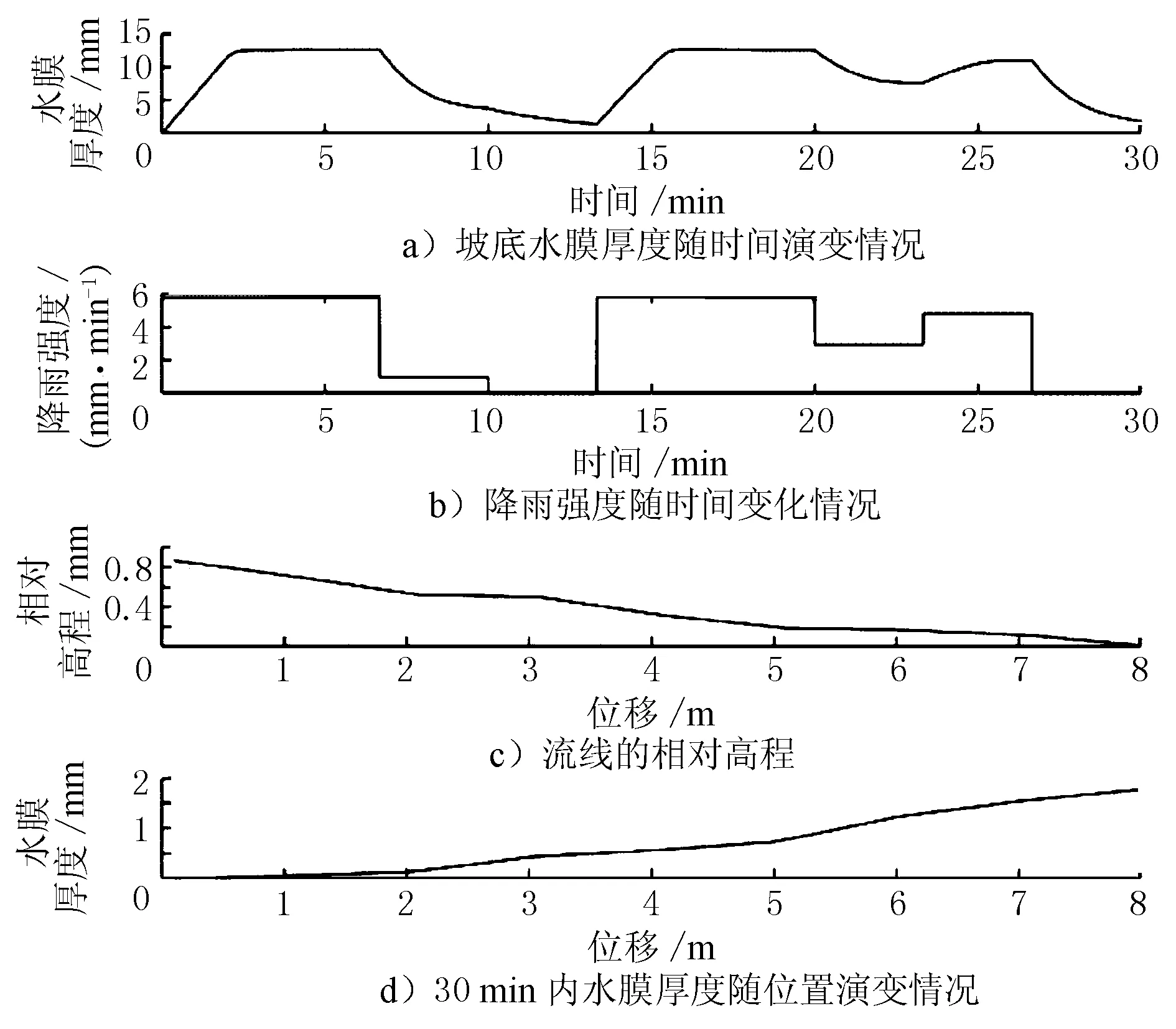
图3 变化降雨强度下水膜厚度演变情况
获取流线上每一点处的水膜厚度时空演变情况见图4。
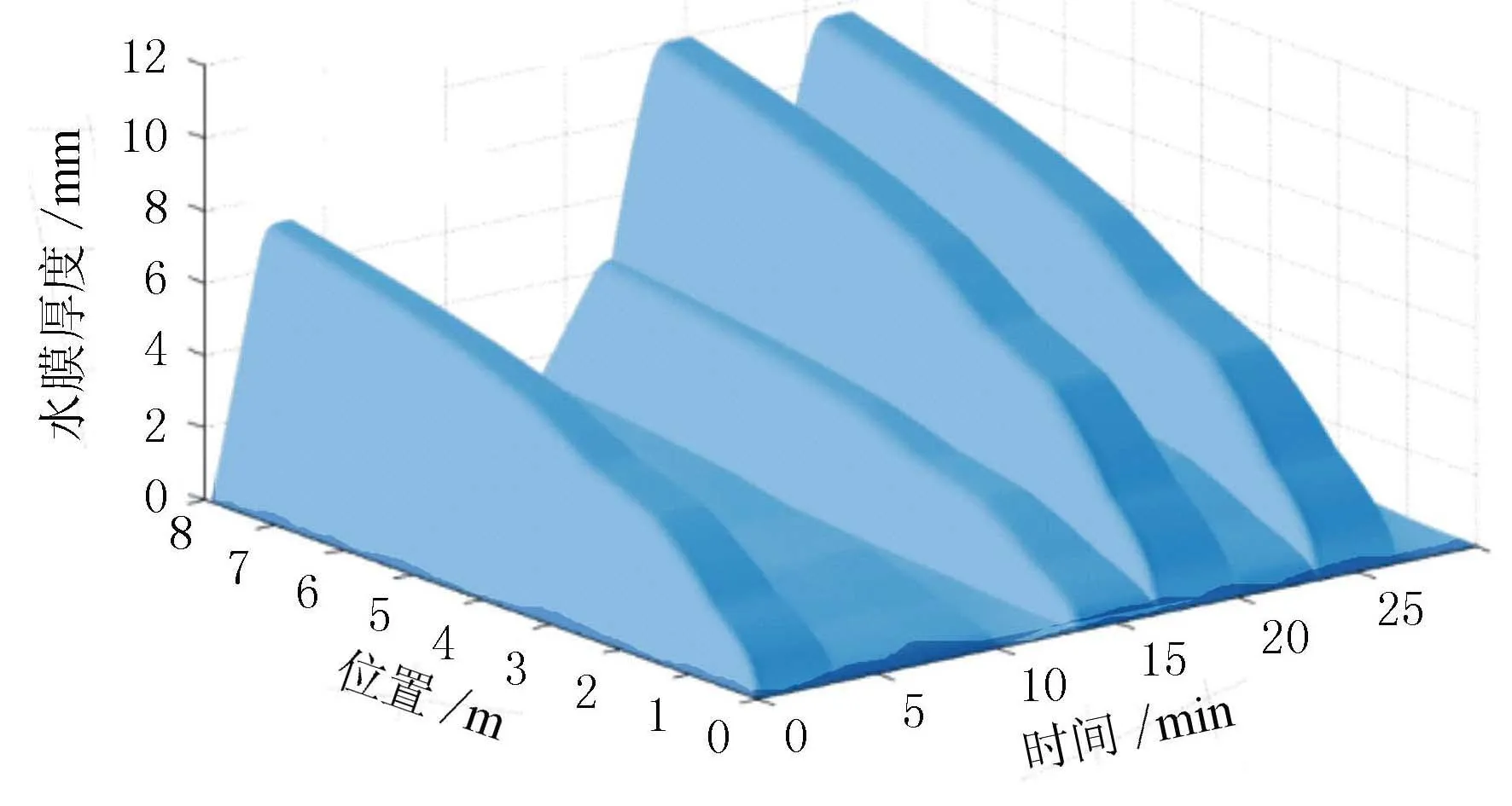
图4 水膜厚度的时空演变特征
由图4可见,流线上每一点处的水膜厚度随时间的变化情况都被非常直观地呈现了出来,相当于得到了该面域的水膜厚度时空演变情况。若将网格划分地更细,得到的结果精度会更高,但与此同时消耗的计算力也越大,考虑到模型预测的实时性,需要根据实际情况在计算速度和精度之间取一定的平衡。
3.3 不同求解方法的对比
本文采用Pressimann四点隐式差分法和MacCormack差分法对控制方程进行求解。随机生成30 min的降雨强度系列计算结果分别见图5。

图5 Preissmann法和MacCormack法的计算结果
由图5可见,2种算法的计算结果基本一致,但在求解过程中,Preissmann四点隐式差分法的计算时间为64 s,MacCormack差分法的计算时间为36 s,后者耗时仅为前者56.25%。考虑到机场系统的数据体量巨大,MacCormack差分法更有助于快速处理并获取道面水膜厚度的动态演变信息,有效提升风险预警的安全裕度。因此在后续研究中,可采用MacCormack差分法对模型进行求解。
3.4 实测验证
北京首都国际机场安全预警平台布设了水膜厚度感知系统,安装了Vaisala MD30遥感式水膜厚度传感器和脉冲式雨量计,实时监测跑道区域的水膜厚度和降雨强度。在安装区域内,跑道横坡和纵坡分别为1.2%和0.15%。
采用该系统2020年11月18日的降雨强度和水膜厚度监测数据,对本文模型进行实测验证,计算结果见图6。
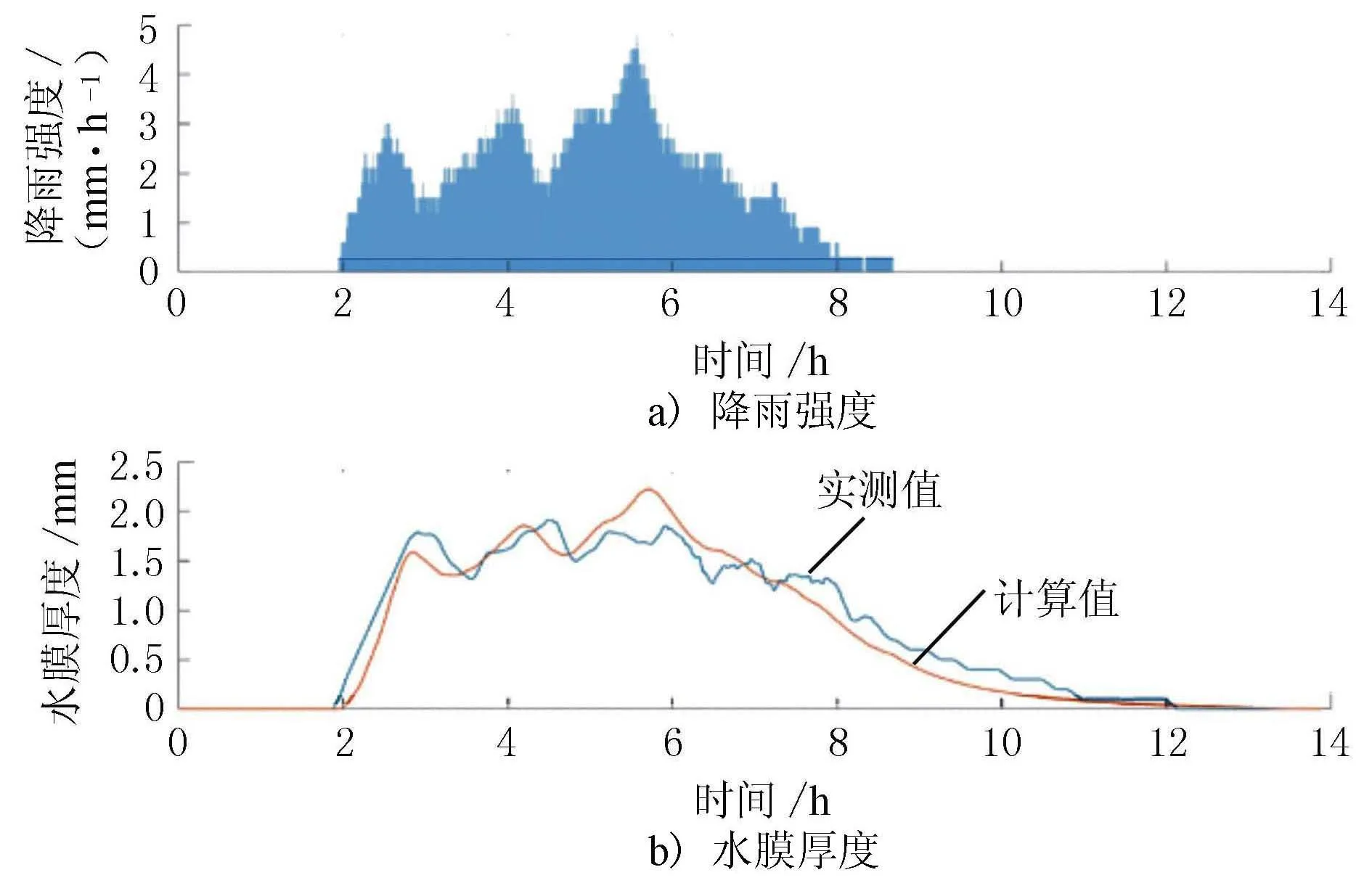
图6 模型计算值与实测值的结果
由图6可见,模型的计算值与实测值具有很好的一致性,均方根误差为0.17 mm。因此,在变化降雨强度下,本文模型具有较高精度,能够精确、实时地描述道面水膜厚度的动态演变。
4 结语
1) 本文基于运动波方程,结合道面动态时空信息,建立了道面水膜厚度动态演变的求解模型,并通过实测数据验证了模型的可靠性。
2) 在恒定降雨强度下,本文模型能够精确计算出道面水膜厚度,平均绝对误差为0.54 mm,平均相对误差为14.9%。
3) 在变化降雨强度下,本文模型能够很好地反映道面水膜厚度的演变特征,并且模型结果与实测数据一致性较好,均方根误差为0.17 mm。
4) 采用了Preissmann四点隐式差分法和MacCormack差分法进行模型求解,后者在求解耗时仅为前者的56.25%,可在后续研究中优先考虑。

