基于扩展卡尔曼滤波算法的港口智能无人内集卡状态估计研究
杨 拯 曾小伟 雷丁瑞 黄雨晴
1 中国交通物资有限公司 2 武汉航科物流有限公司 3 武汉理工大学交通与物流工程学院
1 引言
港口内集装箱卡车运输效率是影响港口作业效率的关键因素之一,准确实时地获取智能无人内集卡的状态参数,是保证其行驶安全稳定的前提。但无人内集卡的有些参数,难以测量甚至不可测量,需要寻找一种更好的获取参数的方法[1]。吴志成等采用卡尔曼滤波算法,建立车辆坐标系搭建二自由度线性车辆模型,对转向系统所需的质心侧偏角和横速度2个参数进行仿真估计[2];安秋兰等首先在Matlab软件的Simulink中设计扩展卡尔曼滤波器,接着通过Carsim软件模拟车辆模型并输出Simulink的算法中需要的状态参数,最后通过2个软件联合仿真来检验算法的准确性以及鲁棒性[3];郝亮等采用扩展卡尔曼滤波算法的基本理论,并使用现阶段可以使用的测量仪器如传感器测得的所需的观测参数,实现在汽车行驶状态下对车辆状态参数的较为精确的估计[4];Liu等主要针对四轮驱动的车辆,采用扩展卡尔曼滤波的相关原理与最小模型误差的相关理论设计出一种新型算法,通过与扩展卡尔曼滤波算法比较可以明显发现参数估计的精确度提升[5];Chen采用扩展卡尔曼滤波算法在车辆行驶过程中对车辆的侧偏角进行研究,通过不同的路面参数以及工况设计的设置进行算法的验证[6];刘丽等建立车辆三自由度系统模型以及采用轮胎模型,研究纵向加速度对车辆系统稳定性的影响[7];张航星等主要对车辆的状态参数以及路面附着系数进行估计,在双移线工况下采用扩展卡尔曼滤波算法的相关理论,在不同的路面附着系数条件下进行仿真分析[8]。
目前,国内主要针对二轴汽车的状态参数估计算法进行研究,对港口多轴智能无人内集卡状态参数估计相关算法的研究比较少,同时相关研究中参数估计算法的所需参数较少,模型建立不够完善。为此,针对港口多轴智能无人内集卡进行研究,建立内集卡动力学模型和魔术轮胎模型并设计扩展卡尔曼滤波算法,对货车状态参数进行估计,并通过Simulink软件与Trucksim软件联合仿真,验证扩展卡尔曼滤波算法在港口内集卡状态参数估计的实时性与准确性。
2 状态估计模型的建立
2.1 动力学模型
为保证扩展卡尔曼滤波算法状态参数估计的准确性,需建立合适的内集卡动力学模型,对智能无人内集卡结构进行整合,将多轴内集卡简化为三轴模型,并对三轴内集卡进行受力分析,以此为基础建立内集卡车体坐标系模型,并以此设计扩展卡尔曼滤波器(见图1)。坐标系中的坐标原点选择在内集卡的车体质心,坐标轴X的正方向是内集卡的前进方向,坐标轴Y在内集卡的车体质心处与坐标轴X垂直。除此之外,还需作以下假设:忽略内集卡行驶过程中的俯仰运动和侧倾运动以及垂直运动;忽略空气阻力等影响;忽略车辆悬梁影响;认为转向系统是刚性的。
图中VX为内集卡纵向速度,VY为内集卡侧向速度,a、b、c为内集卡前中后三轴到质心的距离,δ为轮胎转向角,γ为内集卡横摆角速度,FXL1、FXL2、FXL3分别为内集卡1轴、2轴、3轴的左侧轮胎的纵向力,FYL1、FYL2、FYL3分别为内集卡1轴、2轴、3轴的左侧轮胎的侧向力,FXR1、FXR2、FXR3分别为内集卡1轴、2轴、3轴的右侧轮胎的纵向力,FYR1、FYR2、FYR3分别为内集卡1轴、2轴、3轴的右侧轮胎的侧向力,T1、T2、T3分别为内集卡车轮之间的距离。受力分析可得到状态方程:
(1)
内集卡的质心侧偏角可由内集卡纵向速度与侧向速度计算获得:
(2)
到此内集卡所需的状态参数变量VX、γ、β的相应的方程已经建立。
2.2 轮胎模型
车辆行驶过程中大部分力都是通过轮胎进行传递,建立较为准确的轮胎模型对内集卡模型有关键的作用。魔术轮胎模型是以三角函数组合的形式来拟合轮胎试验数据,得出一套可以同时表达纵向力和侧向力的轮胎模型。在研究中使用的是Pacejka89轮胎模型。
在稳态纯纵滑工况的条件下,内集卡行驶过程中的魔术轮胎Pacejka89模型的纵向力表达式为:
FX0=DXsin(CXarctan(BXSX0-
EX(BXSX0-arctan(BXSX0))))+SVX
(3)
式中,SX0=SX+SHX为纵向力组合自变量;SX为轮胎纵向滑动率,SX>0时为驱动滑转率,SX<0时为制动滑移率;CX为纵向力曲线形状因子;DX为纵向力峰值因子;BX为纵向力曲线刚度因子;BXCXDX为纵向力零点处的纵向刚度;EX为纵向力曲率因子;SVX为纵向力曲线垂直偏移因子;SHX为纵向力曲线水平偏移因子。
根据建立的纵向力方程,可知根据轮胎纵向滑移率与其垂向载荷可以估算轮胎模型的纵向力,并以此为基础构建车辆动力学方程,将方程的输出结果应用到算法之中进行仿真。
在稳态纯侧偏工况的条件下,在内集卡行驶过程中的魔术轮胎Pacejka89模型的侧向力表达式为:
FY0=DYsin(CYarctan(BYaY-EY(BYaY-
arctan(BYaY))))+SVY
(4)
式中,αY=α+SHY,为侧向力组合自变量;α为轮胎侧偏角;CY为侧向力曲线形状因子;BY为侧向力曲线刚度因子;DY为侧向力峰值因子;BYCYDY为侧向力零点处的侧向刚度;EY为侧向力曲率因子;SVY为侧向力曲线垂直偏移因子;SHY为侧向力曲线水平偏移因子。
根据建立的侧向力方程,可根据轮胎外倾角和侧偏角与其垂向载荷估算轮胎模型的侧向力,并以此为基础构建车辆动力学方程,并将方程的输出结果应用到算法之中进行仿真。
本次研究所需的轮胎力输出变量由内集卡状态参数输入计算可得,输入输出变量的表达过程见图2。
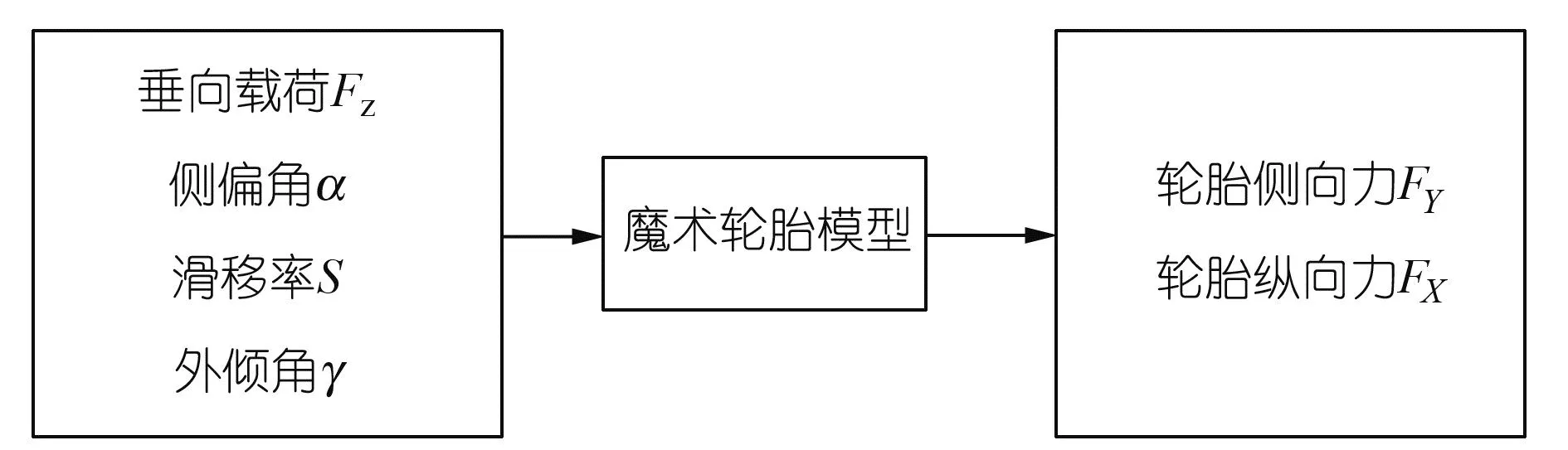
图2 魔术轮胎模型的输入输出变量
3 扩展卡尔曼滤波器设计
3.1 EKF算法
传统的卡尔曼滤波是通过对输入参数的一系列计算,使用贝叶斯定理计算后验概率分布,对状态参数进行较为准确的估计。而扩展卡尔曼滤波算法是将非线性函数在某一采样估计点的附近进行一阶泰勒展开,在不考虑展开式的高阶项的条件下简化得到线性化的系统,之后按照卡尔曼滤波算法的流程原理完成对系统状态参数的最优估计。为了对智能无人内集卡的状态参数进行更为准确的估计,采用扩展卡尔曼滤波算法完成所需参数的估计。
将货车动力学模型和魔术轮胎模型组合后,再将其离散化表示,最后形成的离散化状态方程为:
X(k+1)=f[k,X(k)]+G(k)W(k)BY
(5)
观测方程可表示为:
Z(k)=h[k,X(k)]+V(k)
(6)
此时假定没有控制量参数的输入,过程噪声是均值为0的白噪声,观测噪声同样也是均值为0的白噪声,同时过程噪声和观测噪声彼此独立,以便进行数据处理。卡尔曼滤波算法的迭代过程如下。
(1)状态预测:
(7)
(2)误差协方差预测:
P(k+1|k)=A(k+1|k)P(k|k)·
AT(k+1|k)+Q(k+1)
(8)
(3)滤波增益:
K(k+1)=P(k+1|k)HT(k+1)·
(9)
(4)状态更新:
(10)
(5)误差协方差更新:
P(k+1)=[I-K(k+1)H(k+1)]P(k+1|k)
(11)
3.2 状态转移矩阵
根据上文提到的状态方程,令X=[VX;VY;γ]T作为状态参数。接着将状态参数按采样时间离散化表示后,将当前时刻的X与前一时刻的状态参数建立方程可得:
(12)
扩展卡尔曼滤波算法公式中需要的A矩阵如式(13)所示,即状态转移矩阵,为采用此算法提供了矩阵参数,是设计滤波算法的基础。
(13)
3.3 观测矩阵
观测方程是求解所需变量的方程。在货车状态参数估计中Z是由Vx、ay、γ三个所需变量组成,故所需的观测方程如式(14)所示,所需的经过离散化后的观测矩阵如式(15)所示。扩展卡尔曼滤波算法公式中需要的H矩阵就是此观测矩阵,为此算法提供了矩阵参数,是设计滤波算法的基础。
(14)
(15)
4 仿真与结果分析
在Simulink中使用Function模块编写魔术轮胎模型与扩展卡尔曼滤波算法,得到关于货车的状态参数估计。将Trucksim的实际输出值与扩展卡尔曼滤波算法得出的估算值进行对比,验证扩展卡尔曼滤波算法的准确性和参数估计的可行性。Simulink模型见图3,算法所需要的部分参数见表1。

表1 车辆模型部分参数
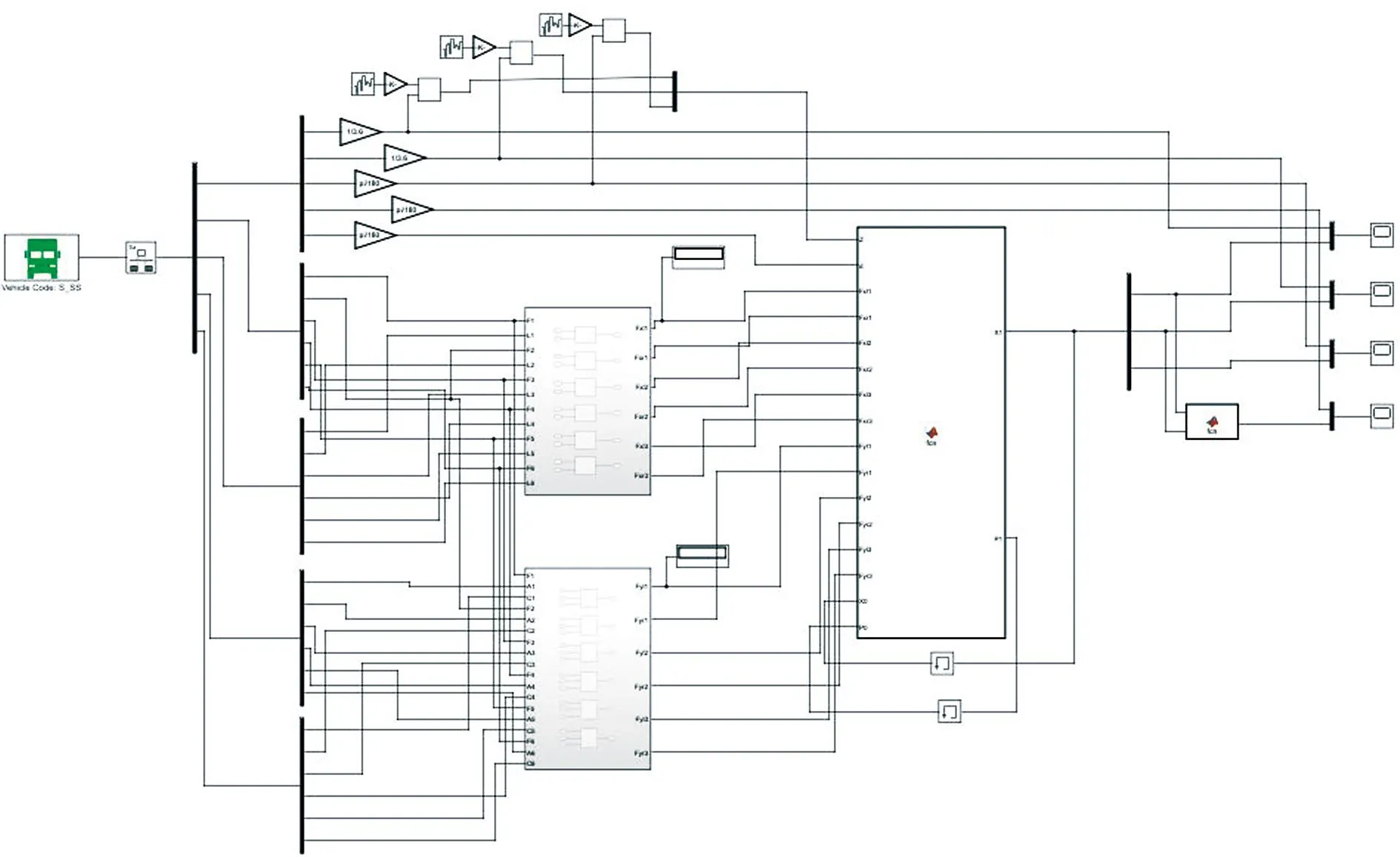
图3 联合仿真模型
为了验证EKF算法的准确性与可行性,选择纵向速度不变条件下蛇形工况进行仿真验证。在Trucksim中设置仿真工况参数,其中纵向速度保持为70 km/h,采样时间T=0.001 s,仿真时间为12 s。
通过仿真,系统实际输出参数与通过扩展卡尔曼滤波算法估算出的参数之间的误差见表2。

表2 真实值与估计值的比较
由表2可知,扩展卡尔曼滤波有着较好的预测效果。其中纵向速度和横摆角速度具有较好的一致性,而质心侧偏角初始的误差较大,但随时间变化估计值趋于稳定,可以得到较为准确的估计值。在蛇形工况下仿真出的3种参数的估算值在实时性与稳定性上较好。
5 结语
针对港口智能无人内集卡难以直接测量的行驶状态参数的估计问题,提出了一种基于扩展卡尔曼算法的间接测量方法,构建了较为完善的魔术轮胎模型与三自由度非线性的三轴货车模型,针对内集卡的纵向车速,横摆角速度和质心侧偏角参数进行估计。采用Simulink软件与Trucksim软件联合仿真的方式,模拟内集卡的行驶工况。对比数据可以得出,利用较容易测得的轮胎力、纵向速度等参数估计难以直接测量的质心侧偏角等参数,扩展卡尔曼算法有着较好的预测效果,同时预测准确性与实时性较高。该间接测量方法为智能无人内集卡状态参数估计提供了一种可行、准确的方案,在一定程度上解决了内集卡安全行驶过程中的信息不完全问题。

