基于红外图像识别的泵站电气设备故障诊断

张 韬

（珠海市斗门区城乡防洪设施管理和技术审查中心）

0 引言

作为电力安全生产的重要载体， 电气设备在人们日常生产生活中起着重要的作用， 电气设备的可靠运转是保证系统安全性和稳定性的基础。随着电气设备运行年限的不断增长， 以及长期高温高压的运行环境， 使得电气设备在运行过程中可能存在一些安全隐患， 设备管理人员如果不能及时发现处理， 可能使这些安全隐患进一步恶化， 导致电气设备出现严重故障， 从而引发安全事故。对于大型泵站而言， 严重的电气设备故障可能导致整个泵站出现瘫痪， 造成严重的经济损失， 因此， 对泵站电气设备开展故障诊断有助于及时发现设备安全隐患， 提高泵站电气设备运行的安全性和可靠性[1］。

随着红外成像技术的不断发展， 红外图像识别技术已逐渐应用到电气设备故障诊断领域[2］。红外图像识别技术的优势在于可以在不影响设备运行的情况下对设备运行状态进行快速检测[3］。在以往的研究中，国内外专家学者们提出了许多基于红外图像识别技术的电气设备故障诊断方法， 一些方法从一定程度上提升了中大型泵站电气设备的故障诊断效率， 但故障诊断精度还有待进一步提高。

1 图像增强算法

电气设备在运行过程中， 设备本身的红外图像与环境背景的红外图像与较大区别， 根据这个特点， 可以首先采用最大类间方差阈值分割法对待诊断电气设备的红外图像进行分割， 将其分解为电气设备红外图像和环境背景红外图像， 二者的类间方差越大， 则说明电气设备与环境背景的区别越大[4］。令电气设备红外图像共有L个灰度级， 其中灰度值为i的个数为n，则总像素的数位可表示为：

则各个灰度值出现的概率Pi可表示为：

式中，Pi> 0且

设以灰度值t为界限将设备红外图像的区域进行划分， 一个区域为背景区， 其像素为范围为0~t， 另一个区域为目标类， 其像素范围为t~L-1。类见方差可表示为：

式中，Pa、Pb分别为背景类像素出现的概率和背景类像素出现的概率；Wa、Wb分别为背景类图像的平均灰度值和目标类图像的平均灰度值；Wt为图像的总灰度值。

对图像进行分割后， 在对电气设备红外图像进行直方图均衡化处理， 即可得到故障特征信息。由于传统处理方法会进一步减小图像灰度级， 使图像的层次感进一步变差， 图像细节丢失严重， 为此， 本文采用阈值C1、C2对其进行限制， 其中C1>C2。当某一灰度直方图值比上限阈值C1更大时， 则该灰度直方图值即为C1， 同理当某一灰度直方图值比上限阈值C2更小时， 则该灰度直方图值即为C2， 当图像灰度值介于C1和C2之间时， 其灰度直方图值不作调整， 则有

式中，H(rk)为处理后的直方图值；h(rk) 为红外图像统计直方图值；k= 0,1,…,L- 1。

经过处理后， 电气设备红外图像的累计直方图F(rk)为：

对式 （5） 中的灰度值进行重组， 可以得到：

式中，D(rk)为均衡化灰度值； [ ]为取整符号。

除了阈值控制外， 还应当考虑细节叠加部分， 因此下线阈值应适当放宽， 通常放宽范围为5%~15%，即可获得相对满意的效果。原始红外图像经过上述处理后仍不能得到非常清晰的画质， 其原因是均衡化处理时使频数较小的灰度值被合并， 无法使直方图值在整个区域内均匀分布， 导致电气设备红外图像出现色斑， 因此还需要进行下一步处理。

首先， 统计被阈值限制后的灰度级个数， 令：

然后， 对电气设备红外图像的有效灰度级进行排序， 并进行等间距处理， 从而使红外图像能够连续，其变换函数为：

经过上述处理后， 即可得到原始红外图像的增强图像， 从而获得可以用于对电气设备进行故障诊断的红外图像。

在灰度图像中， 利用高频滤波方法可以得到图像细节的高频成分， 本文利用拉普拉斯算法对灰度图像的高频成分进行提取， 拉普拉斯算法的计算公式为：

2 卷积神经网络

卷积神经网络 （Convolutional Neural Network，CNN） 是一种结构更复杂的前馈神经网络， 具有多层神经网络结构， 包含输入层、 中间层和输出层[5］。CNN中的神经元响应更及时， 能够更好地进行图像处理， 通过深度学习图像特征， 完成图像识别， 从而实现电气设备故障诊断[6］。

2.1 CNN结构

CNN 的中间层可以进一步划分为卷积层、 激活层、 池化层和全连接层， 相比神经网络， CNN 的不同在于卷积操作。电气设备红外图像经过卷积层处理后， 可以得到底层特征， 再经过池化层的降维以及各层之间的信息堆叠， 将图像特征进行逐层传递， 最后进过全连接层汇总后输出结果， CNN结构如图1所示。

2.2 卷积层

卷积层的主要作用是进行卷积操作， 卷积操作是在卷积核中完成的， 通过卷积计算依次对电气设备红外图像的像素集特征进行提取， 然后利用激活函数进行激活， 即可完成一次从输入到输出的特征提取过程， 卷积操作得到的特征反映了电气设备红外图像的融合特征。在对图像进行处理时， 也可以根据需要将CNN设计为多层， 并逐层进行特征提取。

2.3 激活层

激活层是神经网络实现非线性变换的重要途径， 激活层中含有非线性激活函数， 用以实现非线性变换， 并实现输入量和输出量的同维。常用的激活函数主要有以下三种[7］：

（1） Sgmoid 函 数。 Tanh-Sigmoid 函 数 和Logistic-Sigmoid 函数， 前者为双曲正切S 函数， 后者为回归S 函数， 它们都是非线性函数， 其中， 在零值附近时回归S 函数的曲线斜率更小， 收敛速度也相对更慢。两个函数的共同点在于都需要进行幂指数计算， 网络计算量相对较大， 两个函数均有饱和现象， 在反向传播计算时出现梯度下降的现象。Tanh-Sigmoid 函数和Logistic-Sigmoid 函数表达式分别为：

（2） ReLU 函数。由于Sgmoid 函数在计算过程中存在梯度消失的现象， 为了解决这一问题， 可以引入线性校正单元ReLU， 以加快算法收敛。改进ReLU 函数的表达式为：

式中：a为调节参数， 当a=0 时，f(x)为ReLU激活函数； 当a为固定参数时，f(x)为Leaky ReLU激活函数； 当a为可调参数时，f(x)为PReLU 激活函数。

（3） ELU 函数。ELU 函数是在ReLU 激活函数的基础上提出的， 其鲁棒性更好， ELU 函数的表达式为：

2.4 池化层

池化层又被称为下采样层， 其作用是对图像进行降采样操作， 提取图像的典型特征值， 然后对特征值进行随机池化。池化操作能够将多个值转化为一个值， 从而降低特征图的高度和宽度， 以减少卷积操作的计算量。

2.5 全连接层

全连接层是一种多层传感器， 处在CNN 网络结构的后面， 该层中的神经元与上一层神经元均有连接， 图像特征经过提取并被高度融合， 得到图像的高层特征， 经过回归计算后传输到输出层。

综上所述， CNN 进行卷积操作的计算公式如下：

式中，Xjl为特征图；Mj为卷积计算的子图；f为激活函数；为卷积核矩阵；blj为偏置量。

3 电气设备故障诊断流程

本文首先利用图像增强算法对电气设备图像进行处理， 获得可以用于对电气设备进行故障诊断的红外图像， 然后采用卷积神经网络对电气设备故障进行诊断， 主要诊断流程如图2 所示。

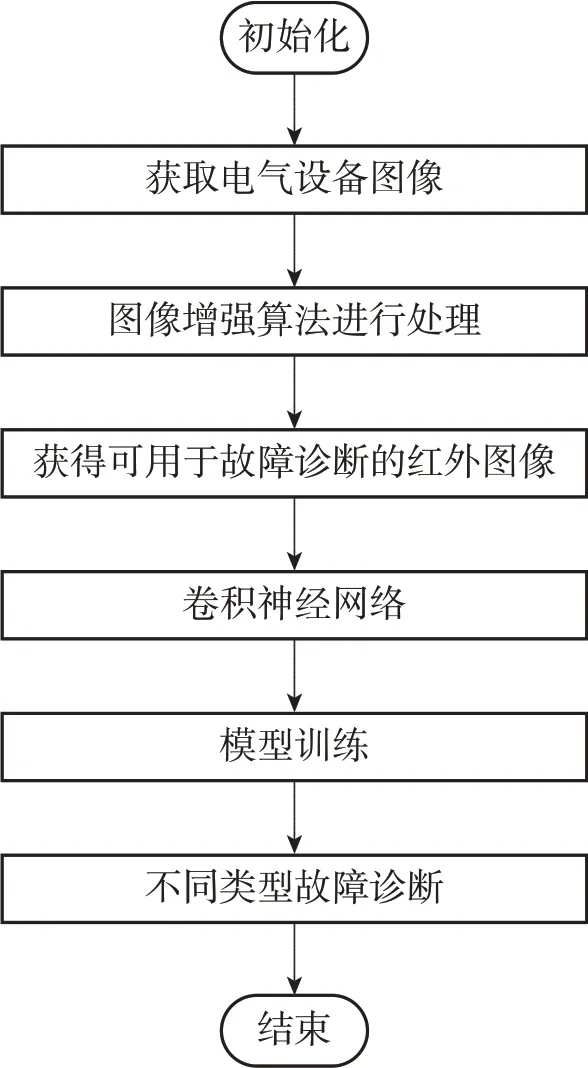
图2 故障诊断流程

1） 获取电气设备图像， 组成图像样本集；

2） 采用图像增强算法对电气设备图像进行处理， 获得对电气设备红外图像；

3） 将红外图像数据输入卷积神经网络， 并对图像进行预处理；

4） 利用CNN 网络对电气设备红外图像进行训练， 得到CNN 故障诊断模型。

5） 利用CNN 故障诊断模型对不同类型故障进行诊断。

4 仿真分析

为了验证本文所提泵站电气设备故障诊断方法的诊断效果， 选取尺寸为1080×1080 的泵站电气设备CT 图像进行仿真分析， 图像类型主要包括正常图像、 电动机碳刷故障和变压器故障等三种， 各类样本数据容量分布表1 所示。

表1 样本容量分布 单位： 张

为了便于CNN 网络输出， 将电气设备的三种状态进行故障编码， 具体如表2所示。

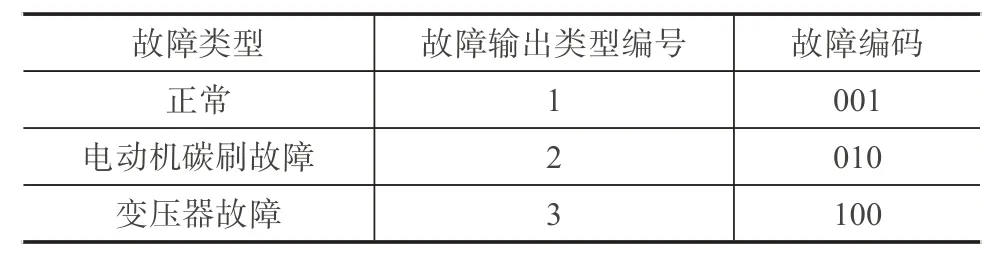
表2 故障类型编号及编码

采用各类样本中的90%样本用于CNN 模型训练， 10%样本用于诊断结果检测， 在Matlab 中进行仿真 分 析， CNN 诊 断 结 果 如 图3 所 示， 由 图3 可 知，CNN模型共出现了2次误诊断， 诊断效果较好。

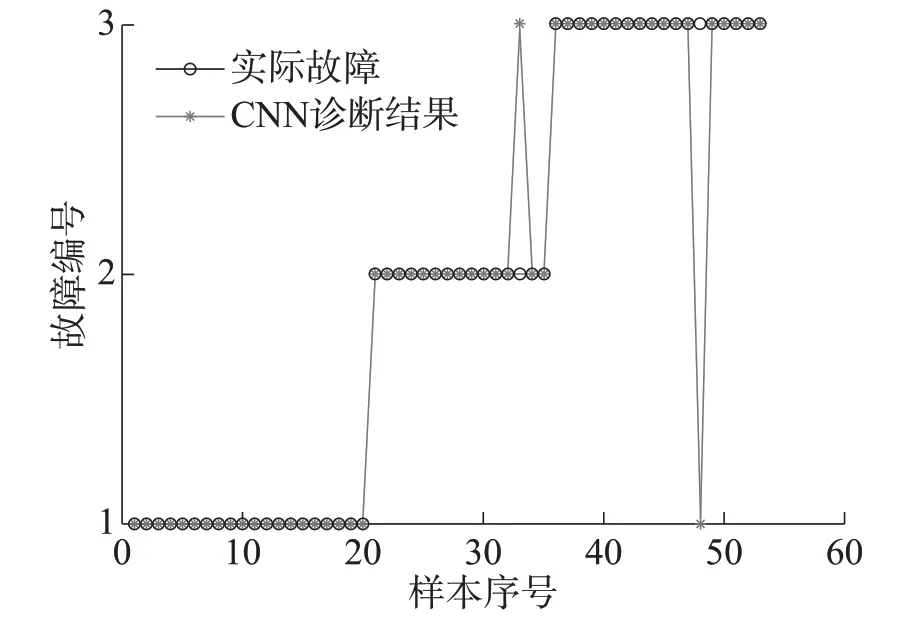
图3 CNN模型诊断结果

为了对比分析， 采用边缘计算方法[8］和机器视觉方法[9］对本文样本图像进行故障诊断， 本文所提方法、 边缘计算法和机器视觉法的误诊断次数和诊断结果的准确率如表3所示， 由表3可知， 三种方法出现误诊断的次数依次为2 次、 5 次和6 次， 诊断结果的准确率依次为96.23%、 90.56%和88.68%， 由此可见， 基于红外图像识别的泵站电气设备故障诊断方法诊断精度更高， 验证了本文所提方法的正确性和实用性。

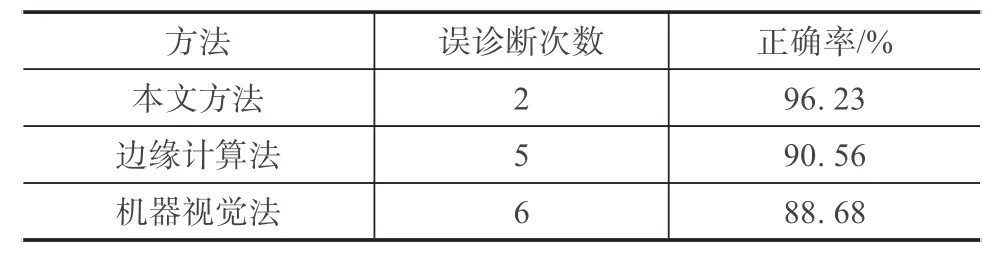
表3 三种方法诊断结果对比

4 结束语

本文首先利用图像增强算法对电气设备图像进行处理， 获得可以用于对电气设备进行故障诊断的红外图像， 然后采用卷积神经网络对电气设备故障进行诊断， 诊断结果表明， 本文所提泵站电气设备诊断方法在诊断过程中出现了2 次误诊断， 诊断效果好于其他方法， 验证了所提方法的正确性和实用性。