基于遗传算法的火电厂机组最优运行研究

钟佳华 刘 刚

（1.浙江浙能电力股份有限公司 2.浙江浙能嘉华发电有限公司）

0 引言

电厂系统运行的主要经济因素是实际发电成本，火电厂实际发电成本主要取决于每小时的燃煤投入。运行成本 （Rm/h） 或燃煤输入 （百万千卡/小时） 直接取决于功率输出。因此， 通过拟合适当的次数多项式， 可以将特定机组的发电成本近似为功率输出的函数， 即该机组的发电功率。

电厂在任何负载条件下运行时， 必须确定每个机组的输出， 以使输送功率的成本最小。有研究试图将输送电力成本降至最低的方法要求在轻负载下仅从最高效的机组供电， 随着负载的增加， 电力可以由最高效的机组提供， 直到达到机组的最大效率点。然后，为了进一步增加负载， 下一个台最高效的机组将开始供电， 并且在达到第二台机组的最大效率点之前不会调用第三台机组， 这种方法未能将成本降到最低[1-2］。

1 遗传算法技术分析

基于遗传算法的火电厂机组最优运行分析是一种利用遗传算法优化火电厂机组运行的方法。火电厂的机组运行涉及诸多变量和参数， 如发电机的负荷、 燃煤用量、 燃烧温度等， 目标是在保证供电稳定和设备安全的前提下， 使得运行的成本最小化或效率最大化。遗传算法是一种启发式优化算法， 模拟了自然界生物进化的过程[3-5］。它通过模拟遗传、 交叉、 变异等操作， 从初始的随机解开始， 逐步寻找到最优解。在火电厂机组最优运行分析中， 可以将机组运行的各种参数作为基因编码， 然后通过遗传算法的操作来不断优化这些参数， 以实现最优的机组运行状态。下面是一个基于遗传算法的火电厂机组最优运行分析的简要步骤：

（1） 问题建模： 将火电厂机组的运行问题抽象成一个数学模型， 将各个参数和目标函数定义清楚。例如， 成本最小化可以作为目标函数， 各种参数如发电机负荷、 燃煤用量、 燃烧温度等可以作为变量。

（2） 编码： 将问题中的各个参数进行编码， 通常使用二进制编码或实数编码， 使得遗传算法能够对这些参数进行操作。

（3） 初始种群： 随机生成一些初始解 （也称为个体）， 每个个体对应一个参数组合。适应度函数： 定义一个适应度函数， 用来评价每个个体的优劣程度。在火电厂的情境下， 适应度函数可能与成本、 效率等相关。

选择： 根据适应度函数的评价， 选择一些个体作为父代， 通常采用轮盘赌等选择方法。

（4） 交叉： 对选出的父代个体进行交叉操作， 产生新的个体， 以引入新的变化。变异： 对新产生的个体进行变异操作， 以增加种群的多样性。更新种群：根据交叉和变异的结果， 更新种群。重复迭代： 重复进行选择、 交叉、 变异和种群更新， 直到达到一定的迭代次数或收敛条件。

（5） 结果分析： 在遗传算法收敛后， 得到一个或多个优化后的个体， 这些个体对应着最优或近似最优的参数组合。对这些参数组合进行解码， 得到机组的最优运行方案。

2 机组优化分析

2.1 成本函数及约束条件

本文中C指生成能源成本，Ci是指第i个单位生产能源的成本， 单位为元/小时 （Rm/h），n是单元总数，则总成本可以写为：

所产生的实际功率Pi是对Ci的主要影响。通过增加原动机转矩来提高单台机组实际发电量， 因此需要增加燃煤支出。

因此， 发电机组i的单台生产成本Ci对于所有实际目的而言仅是Pi的函数。发电机组i的单台生产成本可以近似为：

式中，ai和bi，di是第i个单位的常数。

因此必须选择一组实际生成变量Pi， 其将最小化成本函数。选择需要满足相应条件， 因为有必要同时观察等式和不等式约束， 平等约束是由功率平衡要求强加的约束， 可以写为：

式中，Pd是总功率需求。

由于每台发电机的运行不得超过其额定值或不得低于某个最小值， 因此我们必须约定以下不等式

式中，Pi，min，Pi，max称为发电机负载极限。

2.2 最低成本条件

通过上述分析， 最小发电成本是通过以下条件实现的

式中，λ是拉格朗日系数，是第i台发电机增量成本 （ⅠC） 。

3 遗传算法

遗传算法是一种基于遗传和自然选择原理的优化技术。GA 允许由许多个体组成的种群在特定的选择规则下进化到最大化“适合度”的状态。经典优化方法在寻找全局最优点方面存在局限性， 有时会陷入局部最优点。由于遗传算法是一种多点搜索方法而不是传统的单点搜索方法， 因此遗传算法有望达到全局最优点。此外， 遗传算法只使用目标函数的值， 在搜索过程中不使用导数。与任何其他优化算法一样， GA 通过定义优化变量和成本函数 （目标函数） 开始， 它与其他优化算法一样， 通过测试收敛性来结束。

3.1 变量参数设计

在GA 中， 设计变量表示为二进制数字串0 和1。如果每个设计变量xi，i=1， 2， 3…….n被编码在长度为q的字符串中， 设计矢量使用总长度为nq的字符串来表示， 这个字符串被称为“染色体”。

GA 从一组被称为“群体”的染色体开始。如果使用二进制表示， 则连续设计变量x只能由一组十进制（离散值） 表示。如果变量x（边界xmin，xmax给定） 由q个二进制数字组成的字符串表示， 则可以使用

式中，b相当于是二进制数的离散值。因此， 如果要以高精度表示连续变量， 还需要在其二进制表示中使用大的q值。

3.2 遗传算法在优化中的应用

电厂中机组单元的输出形成变量参数， 因此变量的数量等于机组单元的数量。电厂总负荷、 每个机组的a和b常数以及每个机组发电的下限和上限作为输入。

在解码变量值时， 从二进制到十进制， 使用等式（6）， 机组单元的xmin和最大xmax被视为单位的下限和上限。因此， 任何机组的发电量都保持在该机组的下限和上限之内。目标函数定义为

式中，n为发电机数量，Pi为第i台发电机功率，Pd为负荷总功率。

式中，λi为第i台发电机增量成本。

目标函数的第一部分包含满足负荷需求的相等约束， 第二部分考虑实现相等的增量成本。该函数是为群体的每个染色体计算的， 给出函数最小值的染色体被认为是最适者。染色体根据其适合度进行排列， 然后进行繁殖、 交叉和突变操作。执行多次这样的迭代以实现机组的最优运行方式。

4 实验验证

在MATLAB 中开发了一个利用遗传算法进行火电厂机组优化组合的程序。该程序已针对不同机组数量、 每个机组发电量的不同下限和上限的各种问题进行了测试。这个程序迭代速度较快， 可以给出正确的结果， 这里提供了两个示例案例以供说明。

4.1 案例1

考虑由三台发电机组成的电厂的参数， 机组详细参数如表1所示。

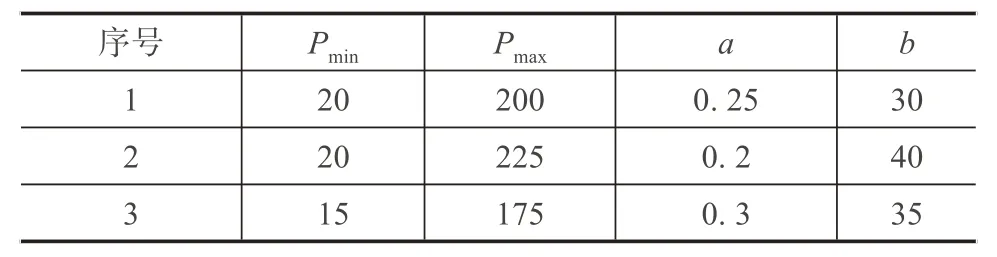
表1 发电机组参数

对于435MW 的电厂负荷， 可以观察到， 机组单元1输出162MW， 机组单元2输出155MW， 机组单元3 输出118MW。每个机组单元的输出相对于几代GA迭代的最佳值如图1 所示。可以看出， 所有的机组单元都有不同的输出下限和上限。对于不同的电厂负荷， 可以使用相同的算法提前准备机组组合。不同机组对不同电厂负荷的分担情况如图2所示。

图1 机组输出相对于迭代的最佳值

图2 不同电厂负荷下各机组分担的负荷

4.2 案例2

以100MW 为步长的从100 MW 至600 MW 电厂负荷的UC表， 如表2所示。

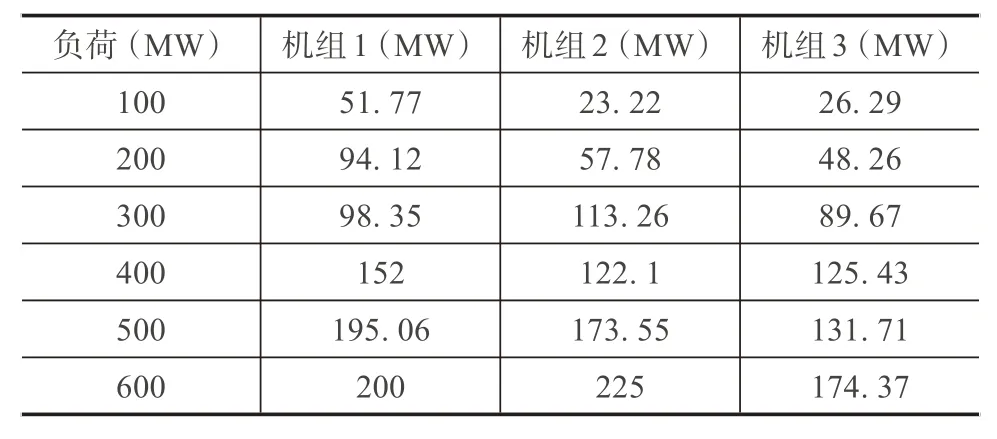
表2 机组组合表

对于任何电厂负荷， 在100MW 到600MW 的范围内， 使用这种由机组分担的负荷可以获得。机组的需求和总发电量之间最大3 MW 的差异可以接受。在这种情况下， 考虑有两台机组的电厂， 每台机组输出功率的最小和最大限制分别为20MW 和125MW。单位的“a”常数分别为 （0.2 0.25） 和“b”常数分别是 （40 30）， 共享的总负载为76 MW。单元机组1 的输出为20MW， 单元机组2 输出50MW。可以看出， 1 号机组将在20 MW的下限下运行。

5 结束语

本文提出了火电厂机组优化的遗传算法， 通过定义一个新的目标 （适应度） 函数， 将基本约束优化问题的最优UC 问题转化为无约束优化问题， 每台发电机上的负载应限制在下限和上限范围内。这是通过定义变量的下限和上限单位输出来实现的， 同时将变量的二进制值解码映射为十进制值。针对各种问题对该算法进行了测试， 达到了预期效果。此外， 使用相同的算法， 可以针对不同的电厂负载预先准备机组组合， 这有助于提前地决定任何电厂负载的每个机组单元共享的负载。