大跨度斜拉桥地震易损性分析

余洁歆, 吴淑婧, 丁传辉, 许莉, 林鑫

(1. 福建江夏学院工程学院, 福建 福州 350108; 2. 福州大学土木工程学院, 福建 福州 350108)

0 引言

大跨度斜拉桥具有高柔度、 低阻尼和优良的抗震性能等特点, 在我国桥梁建设中广泛应用. 受欧亚板块和环太平洋板块地震带的影响, 我国地震发生的次数多且分布范围广. 桥梁作为生命线工程的重要组成部分, 一旦发生破坏, 将导致整条线路处于瘫痪状态, 丧失运输功能[1-4]. 因此, 评估桥梁结构在多种地震强度下的安全性能具有重要意义.

国内外学者围绕大跨度斜拉桥的地震响应问题开展了大量研究工作. Jiao等[5]在20个Ⅲ类场地地震波激励下, 研究主塔、 过渡墩、 副墩和桩在不同地震动水平下的损伤超越概率, 得出斜拉桥倒“Y”形塔的易损区往往出现在塔底、 中塔底和中塔顶3个部位的结论. Zhong等[6]采用数值模拟的方法推导索塔截面的极限状态, 得到准确的斜拉桥体系易损性估计. 马凯等[7]通过云图法和蒙特卡洛模拟研究地震动空间变异性对大跨度斜拉桥易损性的影响, 发现在大跨度斜拉桥进行易损性分析时, 行波效应对纵向漂浮体系影响较小, 相干效应和场地效应对易损性分析影响较大. 以上研究均表明地震易损性分析对抗震设计及地震预警具有重要应用价值, 根据易损性分析结果, 可采取针对性措施提高桥梁的抗震能力.

传统的地震易损性分析方法引入正态分布假设, 其精度取决于所选的评价方法. 但由于震害数据的限制和研究者个体主观因素, 易陷入损伤指标取值不合理的问题, 严重影响易损性分析的准确性. 为更好地反映桥梁工程在实际地震中的破坏, 本研究引入增强动力分析方法(incremental dynamic analysis, IDA)进行大量非线性时程计算, 通过制定合理的量化准则, 衡量桥梁结构或构件在不同损伤状态的极限指标. 基于易损性曲线对结构在不同地震波作用下的动力响应做出定性定量分析, 为实际工程和基于性能的抗震理念提供参考意见.

1 IDA分析设计

地震易损性分析是一种用于评估结构在不同地震荷载下的损伤概率和性能表现的方法. 考虑地震动的随机性, 需要选取充足数量的地震记录以涵盖可能遇到的各种情况. 采用IDA分析方法通过调整系数将所选地震波转化为多条强度幅值不同的地震波, 弥补了单一时程分析在结构性能评估中的不确定性, 从而全面评估结构的抗震性能. 具体步骤如下.

1) 利用有限元软件建立能反映目标结构动力特性的精确有限元模型.

2) 根据场址条件, 选择具有代表性的地震波记录作为分析输入.

3) 根据选定的地震动强度指标, 对所选地震波进行缩放, 生成不同强度水平的地震波.

4) 将调整后的地震波输入有限元模型进行非线性时程分析, 模拟结构在地震作用下的动态响应.

5) 根据分析结果计算结构的损伤状态和性能指标, 并与预先定义的损伤标准进行比较, 确定结构在每个地震强度水平下的损伤程度.

6) 为获得结构或构件在给定地震动强度时, 工程需求参数超过极限状态的概率, 对分析结果进行概率统计. 即

(1)

式中:Pf为损伤概率;D为结构的地震需求参数;Si为第i种损伤状态;I为地震动强度参数;ni为能使结构或构件地震响应超过指定损伤极限状态的地震波数目;N为输入桥梁模型进行非线性时程分析的地震波总数.

7) 以统计得到的损伤概率为纵坐标轴, 地震动参数为横坐标轴, 连接离散点绘制相应构件或者结构的地震易损性曲线.

2 工程算例

以某实例工程大跨度双塔斜拉桥为研究对象, 斜拉桥结构形式采用纵向漂浮体系, 全长1 280 m, 主跨跨径为680 m. 桥梁共分为7跨布置, 其跨径组合为(60 + 90 + 150 + 680 + 150 + 90 + 60) m. 斜拉桥主桥采用钢制单箱多室流线型扁平箱梁高3.5 m, 钢箱梁全宽30.12 m. 每塔两侧各有2 × 21根斜拉索, 呈现双索面扇形布置. 桥墩采用钢筋混凝土结构, 边墩、 辅助墩和主塔墩上均设有竖向支座和约束梁体横向位移的支座.

2.1 有限元模型

采用OpenSees平台建立全桥有限元弹塑性模型, 如图1所示, 整桥共1 031个节点和1 211个单元. 模型计算分析使用CorotCrdTrans局部坐标转换以考虑大位移小应变问题, 使用基于位移的梁柱单元考虑材料非线性问题, 在非线性时程分析前, 进行重力分析以考虑重力影响及结构的应力刚化效应, 合理地模拟大跨度双塔斜拉桥的受力特征. 算例桥梁左右两侧关于主跨跨中处对称, 为方便文章后续相关分析, 对桥墩、 桥塔的名称依次标定为左侧边墩、 辅助墩1、 辅助墩2、 桥塔1、 桥塔2、 辅助墩4、 辅助墩3、 右侧边墩.

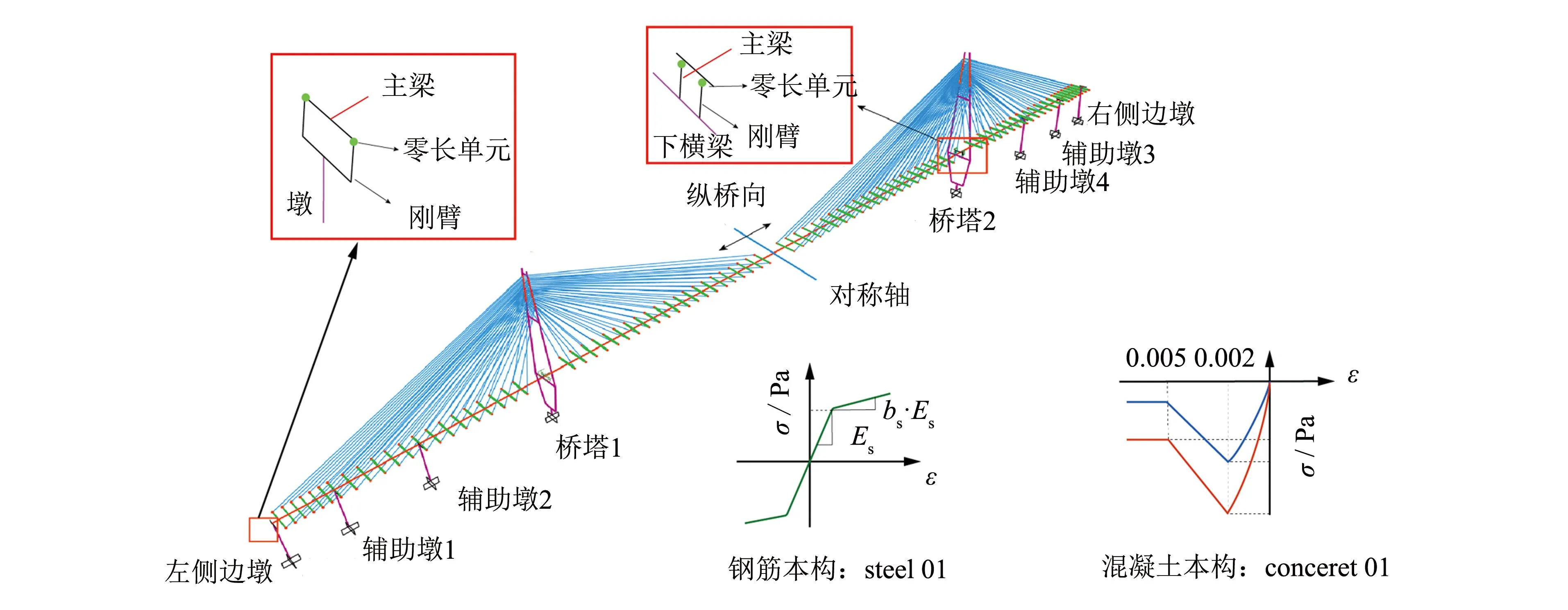
图1 全桥有限元模型示意图Fig.1 FE model of full bridge

2.2 地震动选取

算例大跨度斜拉桥属于长周期结构, 故采用峰值加速度作为地震动强度指标, 通过太平洋地震工程研究中心(PEER)NGA-West2数据库选择100条天然地震动记录, 对所选地震动峰值进行非等间距调幅, 其地震动加速度峰值分别为0.1g、 0.125g、 0.25g等21组数据. 对双塔斜拉桥进行2 100次地震动非线性时程分析, 使用OpenSees计算平台记录桥梁的辅助墩1、 辅助墩2、 边墩墩底、 主塔塔底的曲率和梁端位移数据, 进行易损性分析.

为考虑在具有脉冲特性地震动和非脉冲型地震动作用下, 算例模型的整体响应规律. 采用1999年台湾集集地震时记录到的四条地震动作为输入, 进行算例桥梁的时程分析. 地震波的加速度时程曲线如图2所示, 相关参数见表1. 将峰值速度(v)与峰值加速度(a)的比值作为判断地震波有无脉冲的依据, 数值大于0.2时为脉冲型地震动, 反之则为非脉冲型地震.

表1 近断层脉冲特性与非脉冲特性地震动Tab.1 Near-fault impulse and non-pulse ground motions

图2 所选地震波加速度时程曲线Fig.2 Time history curve of selected seismic wave acceleration

3 地震易损性分析

3.1 损伤指标

损伤指标是对性能目标的量化, 也是地震易损性分析的重要前提. 由于结构的多样性导致难以使用统一性能指标评估各结构, 因此需从构件出发, 对其在不同等级性能水准下做出定量描述. 为此, 国内外研究者对桥梁墩柱提出如位移延性比、 曲率延性比等量化指标[8-11]. 但也有研究[12-17]指出, 墩顶的位移和墩底的曲率变化并不同步, 采用位移延性比指标来量化高墩的损伤状态具有不合理性. 考虑算例斜拉桥的边墩和辅助墩高度均约为50 m, 属于较为细长的构件, 故参照Hwang 等[18]和张菊辉等[19]的研究结果, 采用关键截面曲率延性比指标作为斜拉桥的损伤评判准则, 划分出5种损伤状态, 具体情况如表2所示.

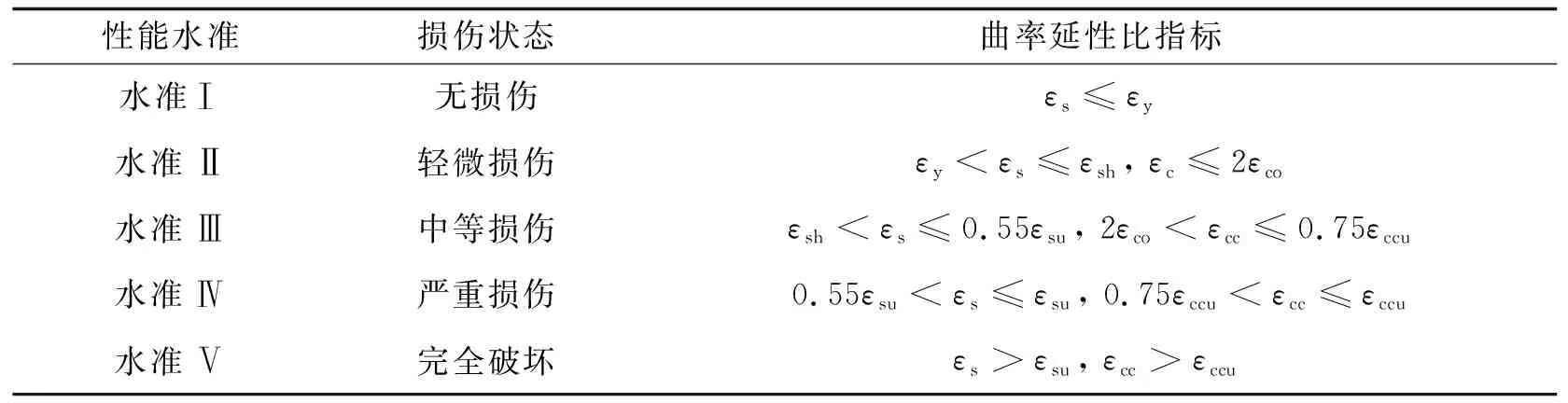
表2 损伤状态及损伤指标描述Tab.2 Damage state and description of damage index

对于大跨度双塔斜拉桥, 结构破坏通常源于主要承力构件的损伤, 故选取左侧边墩、 辅助墩1、 辅助墩2、 桥塔1和边墩支座1, 这5个易损构件的关键截面, 描述其在各级峰值加速度地震作用下的损伤概率. 考虑塔底截面为空心截面, 钢筋直径包含32、 20和16 mm 3种尺寸, 并且钢筋数量较多, 故使用Xtract截面分析软件进行截面建模, 确定截面形状、 材料信息和配筋. 通过ETE-section程序快速剖分保护层混凝土和核心层混凝土, 通过OpenSees平台进行重力分析获得单元竖直方向的轴力, 将轴力通过Xtract软件施加到所分析的截面中. 根据截面应力分布和力的平衡条件, 进行弯矩-曲率分析确定截面曲率水平, 计算结果如表3所示. 采用球形钢支座, 边墩支座型号为QZ4000SX, 辅助墩1和3支座型号为QZ7000SX, 辅助墩2和4支座型号为QZ9000SX. 考虑桥梁实际情况及支座参数, 以位移量化损伤指标, 具体参数见表4.

表3 桥墩墩底及桥塔塔底曲率特性值Tab.3 Values of curvature characteristics at the pier bottom and tower bottom (m-1)

表4 斜拉桥支座位移量化标准值Tab.4 Quantified displacement for cable-stayed bridge bearings (mm)

3.2 易损性曲线

通过非线性时程分析结果获得关键构件最大动力响应, 运用公式(1)确定构件在不同地震强度下的损伤概率, 结合可靠度理论得到地震易损性曲线, 如图3、 4所示. 由于算例桥梁是大跨度双塔斜拉桥, 桥梁沿主跨跨中处呈轴对称状态, 在桥梁构件易损性分析中, 仅展示地震作用下易损概率更高的对称处的构件.

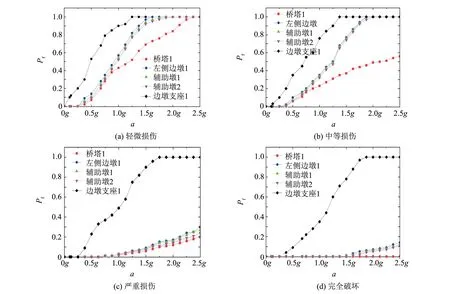
图3 不同损伤等级下桥梁构件的易损性曲线Fig.3 Fragility curves of bridge components under different damage levels

从图3可以看出, 算例桥梁在纵向地震动作用下, 从轻微损伤状态一直到完全破坏, 所选构件的损伤概率大小排列规律一致, 从高到低依次为: 边墩支座 > 桥墩 > 桥塔. 支座与桥墩、 桥塔的易损性相差较大, 当峰值加速度为0.5g时, 左侧边墩支座的轻微损伤概率已达到50%, 发生严重损伤概率已达到20%, 而相同情况下桥墩和桥塔发生轻微损伤的概率均低于20%, 并且未发生严重损伤. 对于桥墩而言, 损伤概率从高到低依次为: 左侧边墩 > 辅助墩1 > 辅助墩2. 由此可见, 在地震作用下纵向漂浮体系的大跨度斜拉桥梁端位移较大, 导致支座极为容易破坏, 应重视此类桥梁在地震作用下的支座响应.

观察图4(a)可知, 当地震波的峰值加速度小于0.25g时, 主塔不发生任何一种损伤; 当地震波的峰值加速度取值为0.375g时, 主塔开始发生轻微损伤和中等损伤; 当地震波的峰值加速度取值大于0.875g时, 主塔开始发生严重损伤, 但是其损伤概率很小.

图4 不同桥梁构件的易损性曲线Fig.4 Fragility curves of different bridge components

观察图4(b)～(d)可知, 在不同地震峰值等级下, 左侧边墩、 辅助墩1和辅助墩2的易损性曲线变化趋势较为相似. 当地震波的峰值加速度取值小于0.25g时, 三者均未发生破坏; 当地震波的峰值加速度取值大于0.25g时, 三者开始发生轻微损伤和中等损伤; 当地震波的峰值加速度大于1.0g时, 三者开始发生严重损伤, 但损伤概率较小.

3.3 脉冲型地震动影响分析

脉冲型与非脉冲型地震时程分析中, 选取算例桥梁主梁梁端位移, 主塔塔底弯矩, 边墩、 辅助墩1及辅助墩2的墩底弯矩作为分析对象, 计算结果如表5所示. 其中TCU067测站的非脉冲型地震波作用下, 桥梁主塔塔底弯矩, 边墩墩底弯矩, 辅助墩1墩底弯矩, 辅助墩2墩底弯矩及塔顶位移最小; TCU036测站的脉冲型地震波作用下结构响应最大.

表5 脉冲型和非脉冲型地震波作用下结构反应Tab.5 Structural response under impulsive and non-pulse seismic excitations

从整体上看, 在具有脉冲效应的地震动作用下, 无论是结构的内力响应还是位移响应都明显大于在非脉冲效应的地震动作用. 对于桥梁下部结构的内力响应, 弯矩从大到小依次为: 主塔塔底 > 边墩墩底 > 辅助墩1墩底 > 辅助墩2墩底. 有无脉冲地震波作用下, 主塔承受的弯矩均为最大, 由此可见, 桥塔为斜拉桥主要受力构件. 同时, 在脉冲地震波作用下主塔塔底弯矩增幅最大, 说明主塔对脉冲型地震动更为敏感. 对于梁端位移, TCU036测站的脉冲型地震动作用约为无脉冲型的8.5倍. 由此可见, 具有脉冲特性的地震动对算例桥梁的主梁梁端位移有显著增大效果. 从图5地震动反应谱曲线可知, 0～2 s周期对应的平台段具有脉冲特性的地震波反应谱值大于非脉冲地震波, 导致算例桥梁在脉冲型地震波作用下的动力响应和内力响应远大于非脉冲型地震动. 有脉冲特性的地震动会使结构响应的峰值急剧增加, 对算例桥梁结构的损伤更大.

图5 脉冲型与非脉冲型地震动反应谱Fig.5 Response spectrum of impulse and non-pulse seismic ground motion

4 结语

采用增量动力分析法, 摒弃传统易损性分析对象服从对数正态分布的假设, 提出改进损伤指标参数优化设计, 绘制算例桥梁在不同损伤状态的易损性曲线, 得到如下主要结论.

1) 针对大跨度斜拉桥制定合理的量化准则, 衡量桥梁构件在不同损伤状态的极限指标. 基于IDA法绘制算例桥梁在地震作用下不同损伤状态的易损性曲线, 解决因引入正态分布假设导致损伤指标取值不合理的问题, 相比于传统方法分析结果更为准确.

2) 通过对算例桥梁在不同损伤等级下的易损性分析可知, 支座与桥墩、 桥塔的易损性相差较大, 表现出较高的损伤概率, 且在严重损伤状态下尤为明显. 说明支座属于桥梁结构的易损构件, 其损伤会直接影响桥梁的正常使用状态, 应在抗震设计中予以重视.

3) 脉冲型地震对大跨度双塔斜拉桥的塔顶位移和内力响应均有显著增大效果, 作为主要受力构件的桥塔在脉冲地震作用下弯矩增幅最大. 在抗震设计中, 应合理考虑近场脉冲型地震动的不利影响, 加强抗震设防能力.