采用自适应最小化置信下限和SMOTE算法的动态代理模型

戚林辉, 潘伟锋, 罗伟林

(福州大学机械工程及自动化学院, 福建 福州 350108)

0 引言

随着计算机技术的发展, 数值模拟在学科分析中获得越来越广泛的应用. 例如, 计算流动力学已被大量用于船舶水动力学分析, 有限元法被广泛应用于结构分析. 数值模拟的优点是精度高, 可以解决学科分析中解析解难以获得的困难, 其缺点是求解复杂问题时耗时较长, 将数值模拟直接应用于工程设计优化中, 其优化效率较低. 针对上述问题, 前人提出基于代理模型的优化策略[1]. 代理模型的基本思想是通过采集具有特征信息的样本点, 构造出高精度的模型, 进而拟合系统设计变量与响应之间的关系. 根据取样策略和构造方法的不同, 代理模型可分为静态代理模型和动态代理模型[2]. 静态代理模型利用一定数量的样本点建立模型, 在优化过程中, 模型和样本数都不变. 为保证足够的精度, 该模型往往需要选取大量的样本点, 导致调用模型次数过多、 效率低下的问题. 动态代理模型在优化过程中根据优化加点准则更新样本点和重构代理模型. 与静态代理模型相比, 该模型具有优化效率高、 模型精度高的优点. 因此, 基于动态代理模型的优化成为近年来的研究热点.

构造动态代理模型的关键步骤包括样本采集、 样本点更新和代理模型构造. 其中, 动态代理模型与静态代理模型的主要区别在于样本更新策略的不同. 常用更新策略包括信赖域方法[3-4]、 重点设计空间法[5-6]、 分割平面法[7-8]、 效率全局优化法[9-10]和模式追踪采样法[11-12]等. 这些策略都是基于试验样本点来进行空间缩减序列采样或空间填充序列采样. 在优化过程中, 最优解附近的样本比较少, 整个样本可视为类不平衡样本, 传统的处理方式为随机过程采样方法, 这种方法容易造成过拟合问题. 为此, Chawla等[13]提出合成少数类过采样技术(synthetic minority oversampling technique, SMOTE). 由于该方法不是在数据空间而是在特征空间中进行采样, 所以准确率高于传统的采样方式. 龙周等[14]应用SMOTE算法, 并结合反向传播(back propagation, BP)神经网络模型, 设计一类动态代理模型, 将其应用于船舶结构的轻量化设计, 与BP模型相比, 径向基函数(radial basis function, RBF)模型具有优良的非线性映射能力, 对样本的要求更低, 所需调整的参数大为减少[15-16]. 刘靖等[17]提出基于SMOTE算法的改进加点策略, 将其应用于BP神经网络代理模型的更新, 在保证模型精度的同时, 能明显提高其优化效率.

本研究提出一种基于自适应最小化置信下限和SMOTE算法(ISMLCBS-DRBF)的动态代理模型. 该模型采用RBF构建, 在优化过程中, 以代理模型预测值与真实模型响应值之间的误差作为确定置信下限公式中的动态平衡常数的依据, 应用多岛遗传算法对动态代理模型进行优化, 然后根据代理模型与真实模型的拟合程度, 更新SMOTE算法的参考近邻数和生成新样本的倍率, 进而更新RBF代理模型.

1 动态代理模型的构建

1.1 径向基函数

对于样本对{xi,yi}(i=1, 2, …,n), 应用RBF进行拟合或回归时, 其基本表达式为

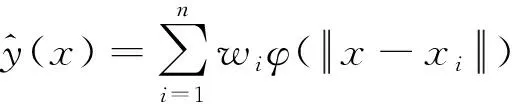
(1)

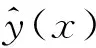
(2)

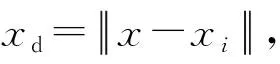
1.2 最小化置信下限准则

动态代理模型样本点的更新主要以3种准则作为依据, 分别是局部加点准则、 全局加点准则、 平衡全局探索和局部开发的加点准则[18]. 目前常用的EI(expected improvement)加点准则是一种较好的平衡加点准则. 但由于该准则在进行全局搜索前, 需要进行足够的局部开发, 因而容易导致效率低下[19]. 为此, 前人提出置信下限准则[20-21], 其最小化目标函数为

(3)

式中:σ(x)为预测标准差;b为非负平衡常数. 常数b的作用为均衡全局搜索与局部开发能力. 当b较小时, 搜索模式偏向于局部开发; 当b较大时, 搜索方向整体偏向于全局搜索. 为获得均衡性能, 采用自适应平衡常数选取策略, 其表达式为

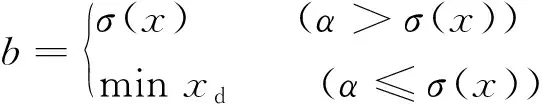
(4)

式中:xd为样本点之间的欧氏距离;α为代理模型预测值与真实模型响应值之间的误差.在初始优化阶段, 由于样本数目较少, 预测的不确定度大,α偏大,b取较大值来进行全局搜索; 随着迭代的进行, 样本数目逐渐增多, 预测的不确定度减小, 全局搜索逐渐向局部搜索过渡, 从而实现全局搜索与局部开发的平衡.

假设RBF的每个确定性响应值y(x)是某个随机过程函数Y(x)的实现[22], 利用n个响应的分布Y=(y(1),y(2), …,y(n)), 可求出假设的随机过程在xn+1处的方差(详细证明过程可参见文献[23])为

(5)

式中:φ为xn+1处基函数向量, 其表达式为

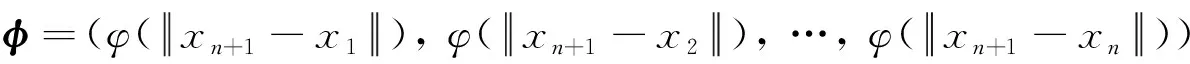
(6)

Φ为对应前n个样本点的基函数矩阵, 其表达式为

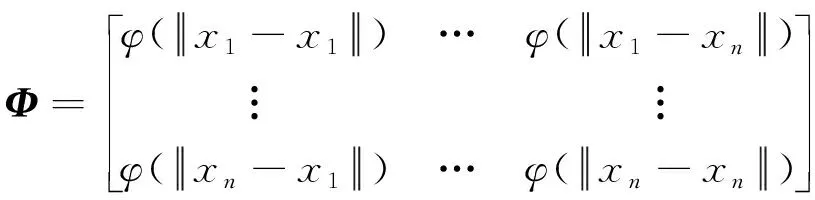
(7)

1.3 SMOTE算法

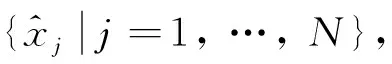
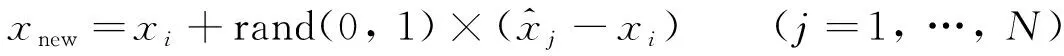
(8)

SMOTE算法的采样是在少数类样本点与其近邻样本点的连线上进行插值. 因此, 新生成的样本点具有通用性. 在本研究中, 以每次迭代优化所得到的最优解为中心, 选取m个样本作为少数类样本集, 进行插值. 对参数L(最优解附近的近邻数)和参数N(每次迭代生成的新样本点倍率)的选取, 采取自适应更新策略. 定义代理模型在k处的样本点xk近似程度参数为

(9)

式中:rk越接近于1, 说明模型近似程度越高, 可减小L, 增加N, 以增强其局部搜索能力; 反之, 则可增加L, 减小N, 并与最小化置信下限相结合, 以增强其全局搜索能力.

1.4 基于ISMLCBS-DRBF动态代理模型的优化策略

一般的, 标准的非线性约束优化问题可描述为

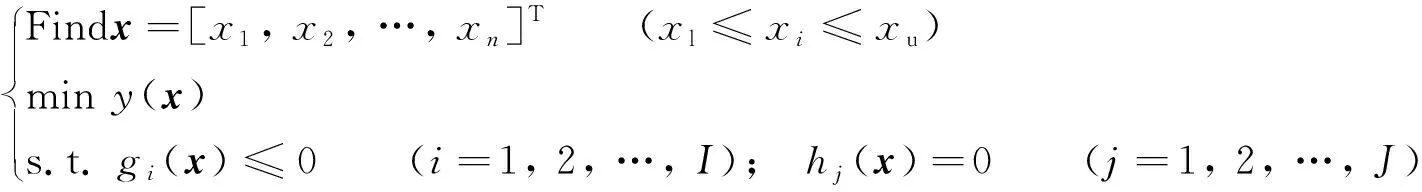
(10)

式中:n为设计变量的个数;xl为设计变量的下界;xu为设计变量的上界.

引入动态代理模型, 并结合最小化置信下限准则, 上述非线性约束优化问题在第K步时可描述为

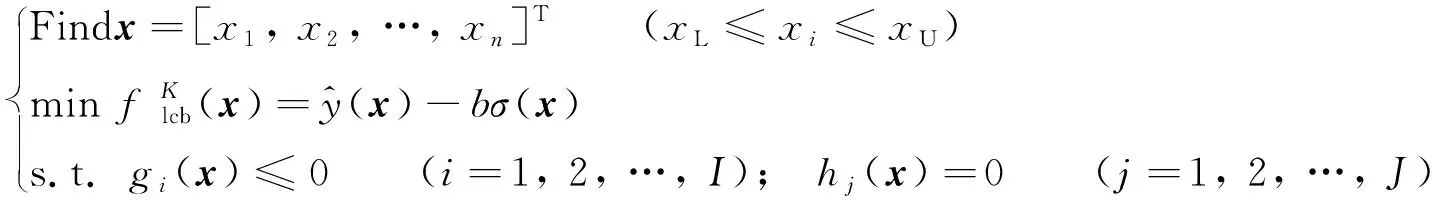
(11)

优化流程如图1所示.

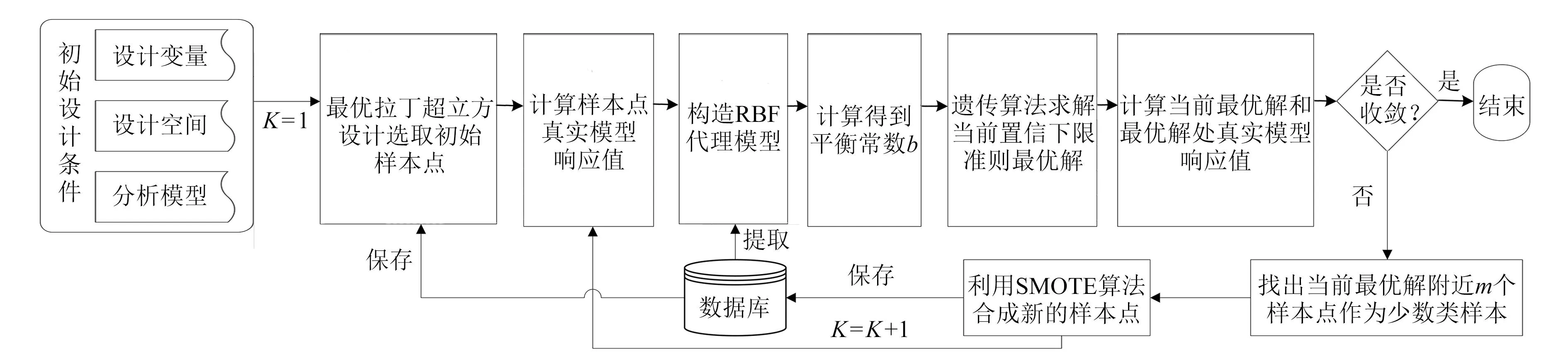
图1 基于ISMLCBS-DRBF动态代理模型的优化流程Fig.1 Optimization process based on ISMLCBS-DRBF dynamic agent model

2 算例测试

选择SC、 GN、 GP和Styblinski-Tang(S-T)函数作为测试算例, 进行ISMLCBS-DRBF模型的有效性验证.

1) SC函数

该函数表达式为

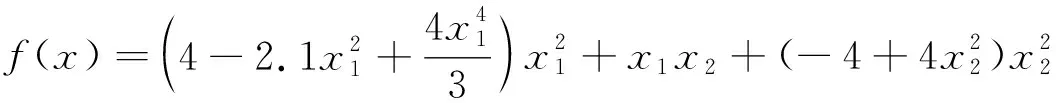
(12)

式中:x1∈[-2, 2];x2∈[-2, 2]. 该函数为两变量、 单峰、 四次函数, 包含6个局部最优解, 其理论全局极小值为-1.031 6.

2) GN函数

该函数表达式为

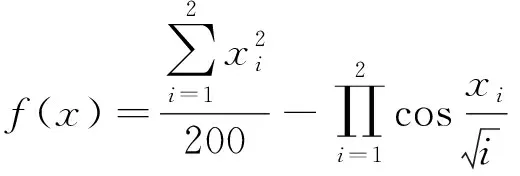
(13)

式中:x1∈[-100, 100];x2∈[-100, 100]. 该函数为两变量函数, 其理论全局极小值为0.

3) GP函数

该函数表达式为

式中:x1∈[-2, 2];x2∈[-2, 2]. 该函数为两变量的四次函数, 包含3个局部最优解, 其理论全局极小值为3.000 0.

4) S-T函数

该函数表达式为

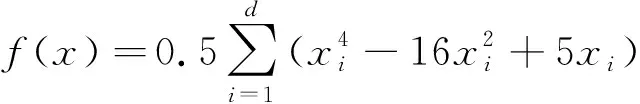
(15)

该函数通常在超立方体xi∈[-5, 5]上计算, 设置超立方体维度(d)为10, 其理论全局极小值为-39.165 99d.

分别利用ISMLCBS-DRBF模型、 基于置信下限的RBF(LCB-DRBF)动态代理模型、 基于SMOTE算法的RBF(SMOTE-DRBF)动态代理模型、 基于自适应置信下限与信赖域的RBF(ALCBTR-DRBF)动态代理模型对上述4个函数进行优化, 并取10次优化的平均值进行分析. SMOTE算法的参数为r=0.5,L1=5,N1=0.5,L2=3,N1=1. 多岛遗传算法参数为Island Number=10, Generation Number=10, Sub-Population Size=10, Migration Rate=0.01, Mutation Rate=0.01, Migration Interval=5. 优化结果如表1所示, 可以看出, 在求解近似最优解(Q)上, 应用本研究的ISMLCBS-DRBF模型所得到的结果具有很高的精度. 在模型调用次数(W)或优化效率上, ISMLCBS-DRBF模型也具有明显的优越性. 尽管在GN函数优化求解时, ISMLCBS-DRBF调用模型次数多于LCB-DRBF和SMOTE-DRBF, 但这两种优化策略会陷入局部最优解.

表1 动态代理模型优化结果Tab.1 Optimization results of dynamic proxy model

进一步对4种优化策略进行鲁棒性分析, 如图2所示. 可以看出, 4种优化策略对SC函数都具有不错的鲁棒性. 在对GN、 GP和S-T函数进行优化时, LCB-DRBF和SMOTE-DRBF优化策略均出现不同程度的波动. 相比之下, ISMLCBS-DRBF和ALCBTR-DRBF优化策略具有更好的鲁棒性.

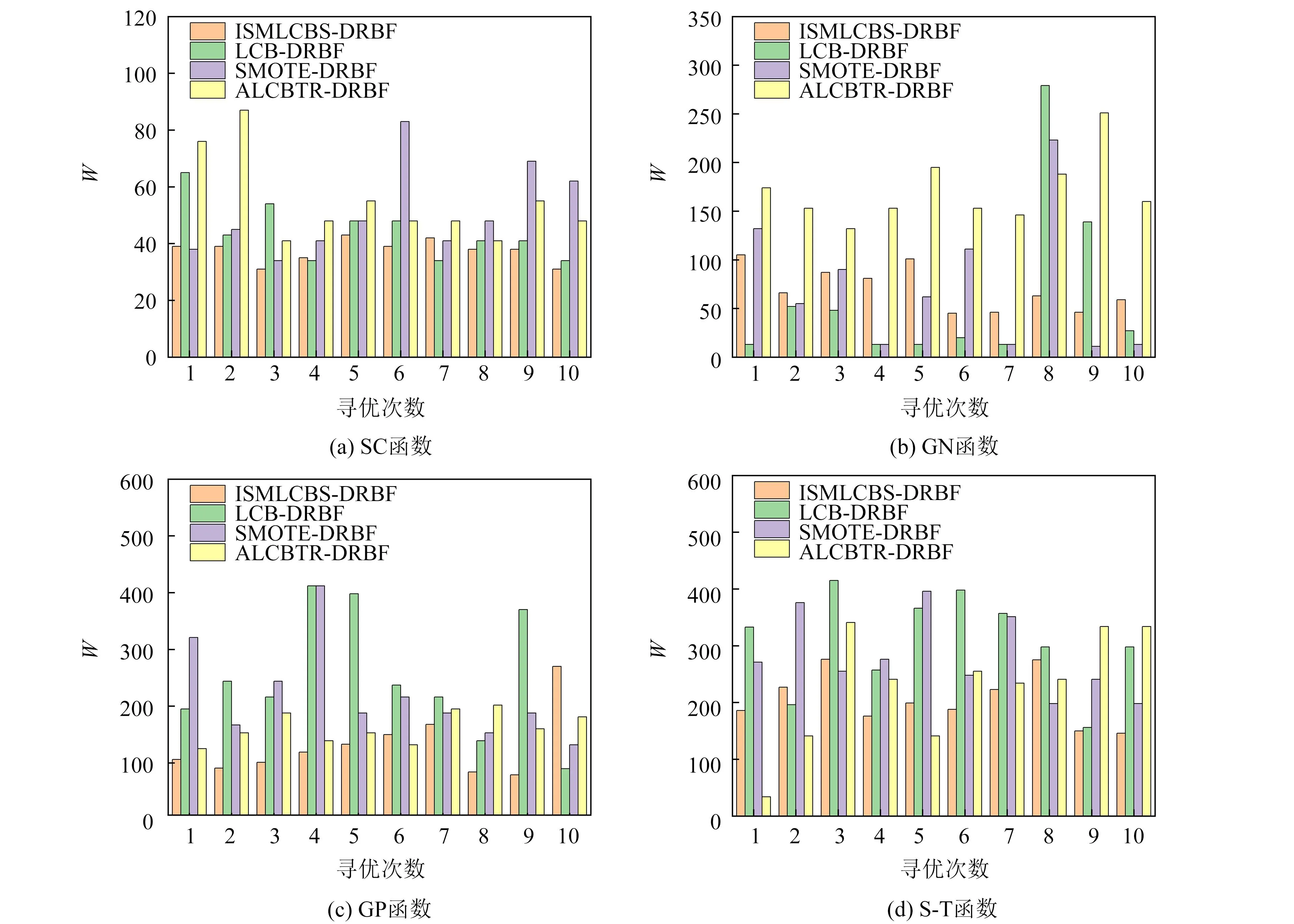
图2 不同优化策略的鲁棒性Fig.2 Robustness of different optimization strategies

3 深潜器耐压舱结构优化设计

3.1 耐压舱模型

基于本研究所提出的动态代理模型优化策略, 对某深潜器耐压舱进行结构优化. 该耐压舱为圆柱体形状, 舱身通过等间距的肋条进行加固, 深度为2 km, 文献[24]中已给出该耐压舱的相关参数. 对该耐压舱进行实体建模和有限元分析. 该耐压壳两端与封头连接, 形成密闭空间. 因此, 在进行有限元分析时, 对壳体两端施加六自由度的完全约束. 强度分析包括相邻肋骨中点壳板处的周向应力(σ1)、 肋骨处壳板的轴向应力(σ2)和肋骨应力(σ3)的计算.根据文献[25], 上述3种应力与屈服极限(σs)的关系应满足

(16)

在稳定性方面, 考虑耐压舱的总体失稳, 临界压强(pcr)与计算压强(p)的关系应满足

pcr≥1.2p

(17)

提取线性屈曲分析中前六阶模态屈曲载荷因子的最小值作为弹性屈曲的安全系数(ns), 则耐压舱理论失稳压强为

pe=p×ns

(18)

有限元分析结果如图3所示, 可以看出, 实际应力分布特点与理论分析[26]一致. 在相邻肋骨之间的中点处出现最大周向应力, 在圆柱壳与肋骨的连接处出现最大轴向应力.

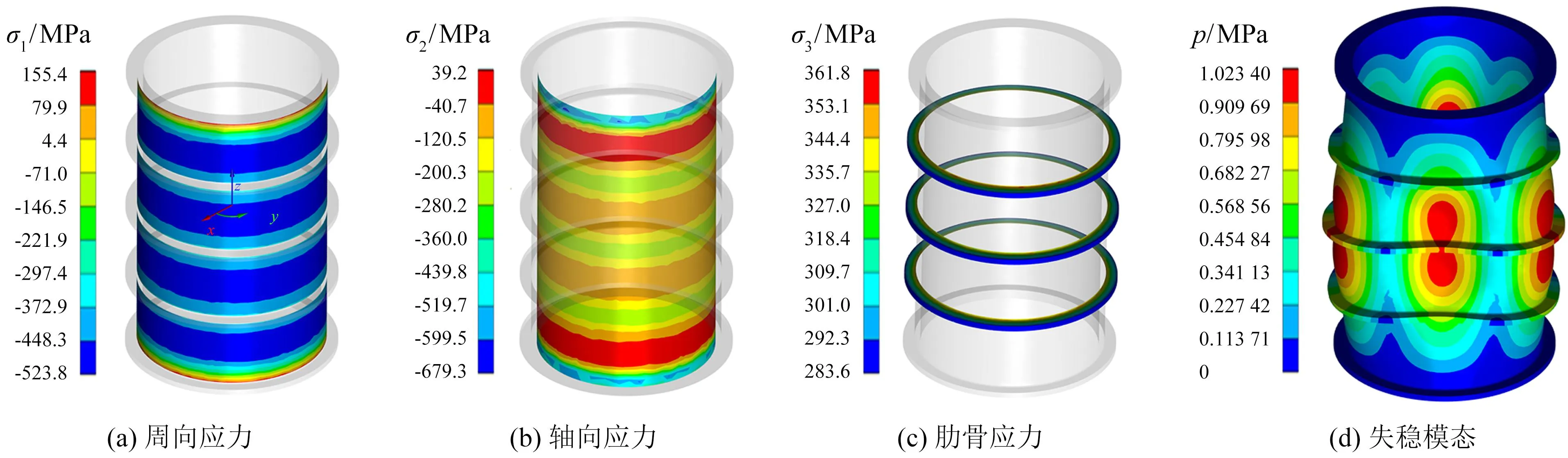
图3 耐压舱有限元计算结果Fig.3 Finite element calculation results of ballast tank

3.2 不同代理模型下的耐压舱结构设计优化

应用Isight软件, 结合所提出的优化策略, 对耐压舱进行结构优化. 设计变量为肋骨高度(h)、 肋骨宽度(w)、 柱壳内半径(rc). 在满足式(16)的应力约束和式(17)的稳定性约束的情况下, 使耐压舱质量(mc)最小, 对应的数学模型为

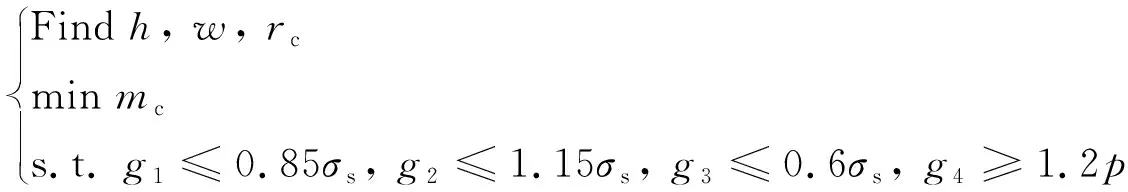
(19)

式中:g1为相邻肋骨中点柱壳处的周向应力;g2为肋骨处壳板的轴向应力;g3为肋应力;g4为稳定性约束.

优化框架如图4所示. 为方便Isight软件运行, 将算法根据不同的功能分为如下6个模块. 1) 样本点采集模块. 实现初始样本点和SMOTE算法所生成的新样本点的采集; 2) 代理模型生成模块. 通过Matlab软件实现代理模型的构建; 3) 寻优模块. 通过Isight软件自带的寻优组件完成代理模型的寻优; 4) 最优解处响应值计算模块. 将Isight软件中的Simcode组件与Workbench软件集成, 实现最优解处真实模型响应值的计算; 5) 收敛判断模块. 通过Matlab软件进行收敛判断, 收敛则优化结束, 输出最优解, 不收敛则进入循环模块; 6)循环模块. Isight软件可在优化不收敛时通过Loop组件进行下一次优化循环.

图4 深潜器耐压舱结构优化过程Fig.4 Optimization process of ballast structure of deep submarine vehicle

所提出的动态代理模型的优化结果如表2所示. 分析模型的调用次数为81次, 耐压仓质量最优解为22.887 kg, 有限元结果为22.884 kg. ALCBTR-DRBF动态代理模型的结果显示, 分析模型的调用次数为95, 最优解质量为22.930 kg, 有限元结果为22.922 kg. 由表1结果可知, 该模型的优化效果比其他几种模型更好. 因此, 选择该模型作为对比模型. 相较于ALCBTR-DRBF模型, 本研究所提出的动态代理模型调用模型次数更少、 优化精度更高, 且耐压舱质量减少28.55%, 预测最优解与有限元分析结果的误差仅为0.013%.

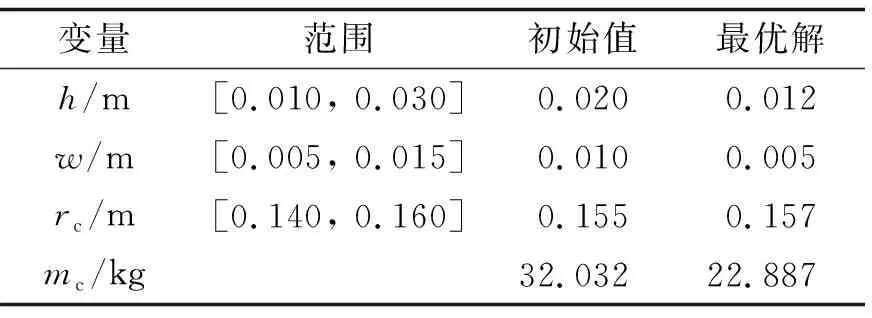
表2 设计变量和目标函数优化结果Tab.2 Design variables and objective function optimization results

图5为多岛遗传算法对肋骨高、 肋骨宽、 内径、 质量等设计变量的寻优历程. 其中, 黑色点、 红色点、 绿色点分别代表可行解、 不可行解、 最优点.

4 结语

结合最小化置信下限和SMOTE算法的特点, 提出一种动态RBF代理模型, 可在全局寻优和局部寻优之间形成平衡. 将所提出的ISMLCBS-DRBF优化策略应用于4个数学算例和深潜器耐压舱的优化中, 结果显示, 相较于其他优化策略, ISMLCBS-DRBF优化策略具有更好的精度和效率. 本研究未考虑初始样本点的选取对后续优化的影响, 此部分内容将在后续研究中进行探讨.