集成电路二划分的一维泊松方程方法

余永昕, 潘萍梅, 朱文兴

(福州大学离散数学与理论计算机科学研究中心, 福建 福州 350108)

0 引言

近年来, 随着集成电路制造工艺的迅速发展, 集成电路产业已经进入了超深亚微米和纳米工艺时代, 芯片的集成度进一步提高. 一块芯片上所能集成的电路元件越来越多, 加上存储空间的局限性和封装工艺的限制, 对超大规模集成电路(very large scale integration circuit, VLSI)设计方法提出了新的挑战. 为降低设计复杂度, 需要将电路划分为更小的模块, 而二划分算法则是所有划分算法中最基础、 最重要的部分.

平衡二划分问题是NP(non-deterministic polynomial)难问题, 无法在线性时间内得到其最优解. 目前, 集成电路平衡二划分的算法主要可以分为四种类型: 全局算法[1-2]、 启发式迭代改进算法[3-4]、 进化算法[5-6]和多级划分算法[7-10]. 其中, 全局算法虽然在理论上能得到二划分问题的最优解, 但因为其存在复杂度过高的不足, 故仅适用于极小规模的问题; 启发式迭代改进算法通过改变顶点的所属划分迭代优化划分的割边数量, 算法一轮迭代的复杂度较低, 但迭代轮数无法控制, 并且算法具有极强的局部性; 进化算法具有较强的全局搜索能力, 但无论是将其直接用于二划分问题的求解, 或是与其他二划分算法结合使用, 皆因运行时间过长使得这类算法难以应用于实际问题; 多级划分算法是目前应用最广泛的二划分算法, 其划分质量与运行时间综合表现最优.

多级划分算法包含粗化阶段、 初始划分阶段和细化阶段, 粗化阶段通过缩合顶点降低电路规模, 初始划分阶段在粗化的最终电路上执行划分算法并择优作为初始解, 细化阶段逐步恢复电路并优化划分结果. 由于初始划分阶段得到的初始解存在明显的提升空间, 而且近年来集成电路布局算法的研究得到显著推进[11-12], 所以本研究将二划分问题转化为离散布局问题. 在全局布局阶段将其松弛为连续布局问题, 并用提出的算法进行求解, 在合法化阶段将求得的解映射到对应的离散解空间, 最后在详细布局阶段使用局部优化算法进行优化. 实验结果表明, 提出的划分算法直接用于二划分或嵌入到多级划分算法中的初始划分阶段都是有效的.

1 相关介绍

1.1 集成电路二划分问题描述

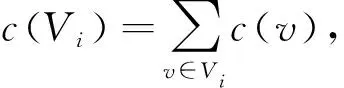
(1)

其中:ε称为平衡参数, 即允许两个划分子集之间权重差异的大小.为后续书写方便起见, 将c(V1)、c(V2)的下界用L表示, 上界用U表示.式(1)可转换为

L≤c(V1),c(V2)≤U

(2)

两个子集之间存在的连边又称为割边, 每条割边e满足:e∩V1≠φ且e∩V2≠φ.则cuts(H,V1,V2):={e:e∩V1≠φ且e∩V2≠φ}表示一个二划分的所有割边, 所有割边的权重之和可以表示为

(3)

结合式(2)和式(3)可建立集成电路二划分问题的数学模型为

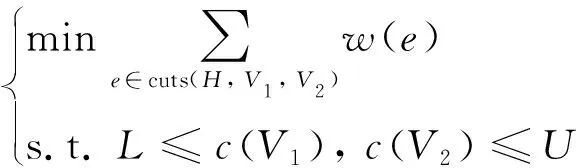
(4)

1.2 集成电路布局问题介绍

在电路布局问题中, 每个单元vi拥有宽和高两个属性, 并通过坐标(xi,yi)表示其中心位置.而电路布局问题主要研究在给定的布局区域W×H中, 如何在满足平衡性约束的条件下, 根据一个或多个目标, 确认每个单元所处的位置. 其中, 平衡约束要求顶点在整个布局区域内的分布是均匀的. 在满足均衡性约束的前提下, 布局算法主要通过布局的半周长线长(half-perimeter wirelength, HPWL)来衡量布局的质量. HPWL的定义为

电路布局算法目前主要分为3个阶段: 全局布局、 合法化与详细布局. 其中, 全局布局阶段的目的是生成一个合法化算法可接受的解. 对于一个解是否可接受的判定与具体使用的合法化算法有关, 一般与单元(顶点)间重叠面积的大小相关; 合法化阶段, 将全局布局的结果(往往不是电路布局的合法解)调整为一个电路布局的合法解; 详细布局则是在合法化的基础上, 以保持解的合法性为前提, 通过对解的细微调整, 提升解的质量, 并返回一个最终的布局解.

全局布局阶段的目标是尽可能降低布局的半周长线长和单元间的重叠面积, 合法化阶段使用的策略包括贪心地将不合法的单元移动到合法位置、 动态规划、 线性规划、 网络流算法等方法; 详细布局阶段使用的策略有分支定界法、 模拟退火、 单元交换、 动态规划等方法.

2 模型的建立与求解

2.1 布局模型

为满足转换后的离散布局问题与二划分问题等价, 设立如下模型: 将区间[0, 1]与区间(1, 2]分别代表二划分中的两个划分块, 设超图中每个顶点是长度1的线段, 顶点v的中心坐标xv表示顶点位置及顶点所属划分块, 令xv∈{0.5, 1.5}, 模型如图1所示.沿用划分问题的记号, 两个划分块可定义为V1={v:xv=0.5,v∈V},V2={v:xv=1.5,v∈V}.

图1 布局模型Fig.1 Placement model

用Φ(e,i)表示超边e在划分块Vi中关联的顶点个数, 那么可以定义划分产生的割边集合cuts(H,V1,V2)={e:Φ(e, 1)>0且Φ(e, 2)>0}.

从图1可以看出, 当所有顶点的中心都处于0.5或1.5处时, 该布局模型的HPWL(x)等于二划分问题(4)中的目标函数. 即

设超图的顶点数|V|=n, 于是二划分问题(4)等价于如下离散布局问题的数学模型, 即

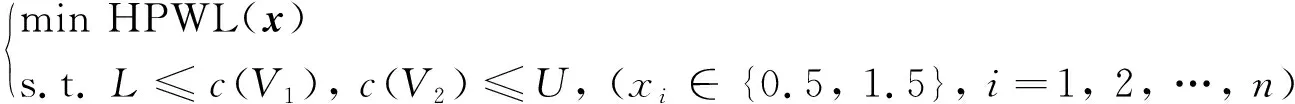
(5)

2.2 一维泊松方程推导结果

鉴于泊松方程在布局算法中表现优异, 使用泊松方程建立的密度函数作为优化中的罚函数. 参考ePlace[11]与pPlace[12]关于二维泊松方程的讨论, 结合本研究的布局模型, 得到一维泊松方程形式及其边界条件, 有

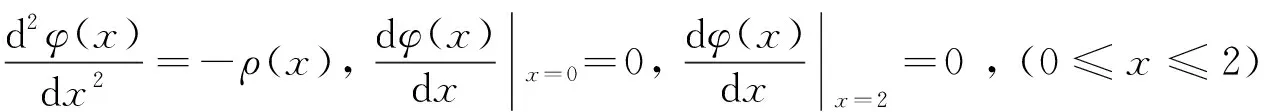
(6)

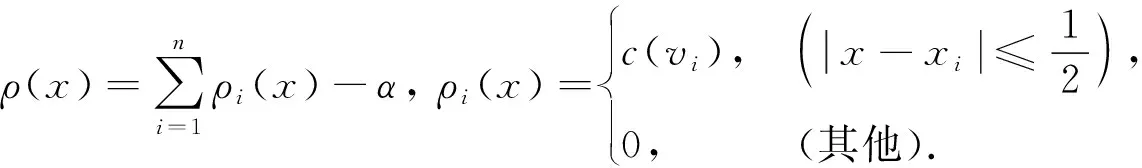
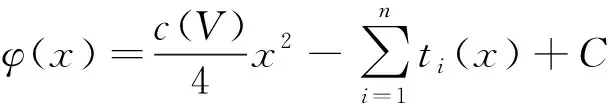
(7)

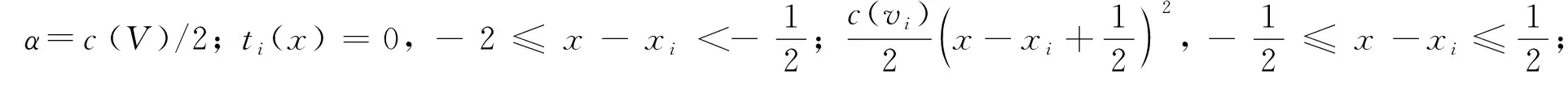
当所有的顶点权重均匀地分布在0.5与1.5处时, 全局的密度分布是均匀的. 根据φ(x)的形式可知, 对所有顶点求φ′(x)需要O(n2)的时间复杂度.为降低时间复杂度, 用φ′(0.5)和φ′(1.5)的加权平均值近似顶点的导数, 权重为顶点与两个部分的重叠面积.即

φ′(xi)=(1.5-xi)φ′(0.5)+(xi-0.5)φ′(1.5)

(8)

由式(8)可证明, 当0≤x≤2且∀1≤i≤n, 0≤xi≤2时,φ′(0.5)=φ′(1.5)=0的充要条件为

这说明式(8)的计算方式是可行的.

2.3 松弛问题求解

将式(7)作为惩罚项加入模型(5)的目标函数中, 可得到全局布局阶段要优化的目标函数为

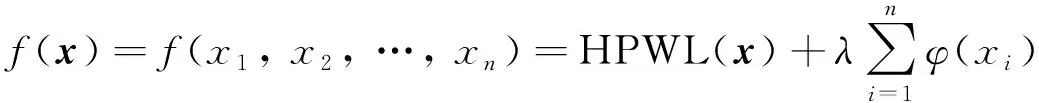
(9)

同时, 将xi的取值范围松弛至[0.5, 1.5]. 于是, 原本离散的布局问题的数学模型(5)变成一个连续优化问题的数学模型为

并且使用Nesterov[11]方法进行优化.

在合法化阶段, 需要将全局布局阶段得到的连续解, 映射至原问题离散解空间上. 因此, 将所有顶点的坐标调整为

从而得到该离散布局问题的一个合法解.

由于HPWL和割边等价, 在详细布局阶段使用FM算法对解进行迭代优化. 其中, 顶点移动意味着顶点从0.5的坐标位置移动到1.5, 或者从1.5移动到0.5. 迭代结束后, 便得到问题的最终解.

2.4 算法流程

2.4.1初始解设置

利用随机算法、 装箱算法、 宽度优先搜索算法、 贪心图增长算法[13]、 标签传递算法[14]在划分过程中, 对顶点确认所属划分的顺序产生本研究提出的划分方法的初始解. 除随机算法外, 其他划分算法有一共同特点: 顶点确定所属的划分存在先后次序, 更符合算法设定标准的顶点越早加入划分. 由于宽度优先搜索算法往往在搜索到占总顶点权重一半的顶点时停止搜索, 将搜索到的顶点归入划分块V1, 这就使得另一划分块V2中的顶点并没有加入划分的顺序.因此, 对宽度优先搜索算法进行修改, 采用如下方式获得初始解: 当搜索到顶点权重一半的顶点时搜索并不停止, 而是持续搜索整张图, 并记录下最后一个搜索到的顶点, 从这个顶点出发, 再利用宽度优先搜索, 获得V2中顶点的顺序. 如此, 在得到两个划分块各自加入顶点的顺序后, 按照顺序分别将一定比例的顶点放置在0.5与1.5处, 并将剩余的顶点放置于1.0处.

2.4.2图结构转换

无论是HPWL还是关于HPWL的近似模型LSE、 WA等, 只有超边上坐标处于最左或最右的顶点的偏导数非0. 而对于划分问题而言, 一条超边若为割边, 则需要优化的顶点往往不止有左右端两个顶点, 因此, 对于每条割边而言, 在优化过程中, 不仅最左与最右的两个顶点需要有收缩的趋势, 其他顶点也应该有收缩的趋势. 所以, 在对超图进行优化时, 将超图转化为星型图以达到该效果. 星型图将超图中的每条超边e转化为一个顶点, 该顶点与对应超边所关联的顶点邻接.星型图G(V′E′)的定义为

其中, 所有超边转换而来的顶点v′(v′∈E⊂V′)的坐标由其对应超边关联的顶点的坐标加权得到.即

由于这些顶点只起标识作用, 不影响划分结果, 因此并不直接参与优化, 只在所有顶点完成一轮移动后, 根据公式更新其坐标, 也不考虑其权重.

2.4.3预处理

由于HPWL(x)非二阶可微, 参照ePlace[11]的调整策略, 用顶点的度代替HPWL(x)的二阶偏导数为

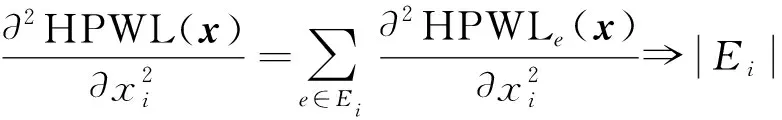
(10)

其中:Ei代表所有与顶点vi相连的超边的集合.

由于密度函数非凸, 参照ePlace[11]的做法, 采用如下方法估计其二阶偏导数, 即

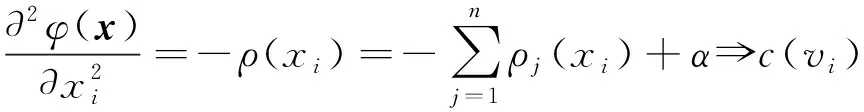
(11)

由式(9)～(11)可得

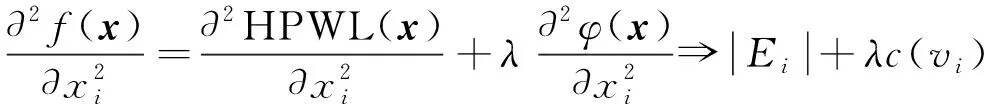
(12)

于是, 海森矩阵的估计为

(13)

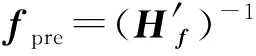
2.4.4罚参数更新

为了使初始时密度函数的导数与线长部分的偏导数平衡, 设置罚参数的初始值,有

罚参数的更新方式为λk=μk·λk-1.ΔHPWLk=HPWL(xk)-HPWL(xk-1),μ0=1.04.其中, ΔHPWLref表示每轮迭代所期待增加的线长值, 将其定义为ΔHPWLref=10%·HPWL0, HPWL0表示初始解对应的线长.

2.4.5算法伪代码

本研究提出的二划分方法先是利用调整后的宽度优先划分算法得到两个划分块加入顶点的顺序, 以此获取布局模型的初始解, 然后使用Nesterov方法进行优化. 将优化后的解进行合法化处理, 并使用局部优化算法进行改进. 具体的算法伪代码如下所示.

算法: 平衡二划分的非线性布局方法

输入: 超图H(V′E′), 固定顶点权重比例β, 平衡参数ε

输出: 超图H(V′E′)的划分结果

1: (vec1, vec2)=simple_bipartition(H)//使用简单的划分算法得到顶点加入划分的顺序

2: 星型图G(V,E)=star_graph(H,ε)//超图转换为星型图

3: intial_placement(vec1, vec2,β)//获得布局初始解

4:k=1//迭代轮数初始化为1

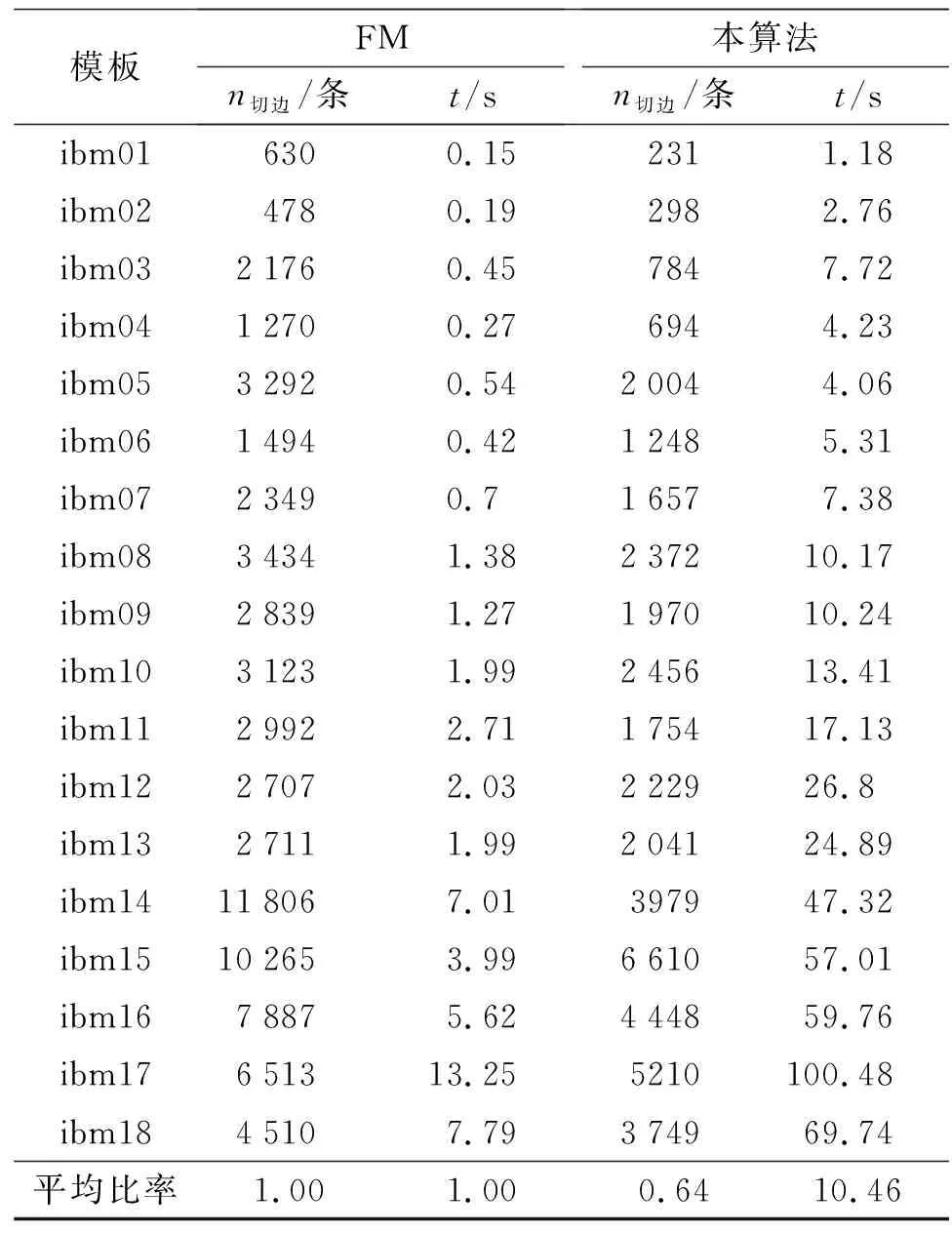
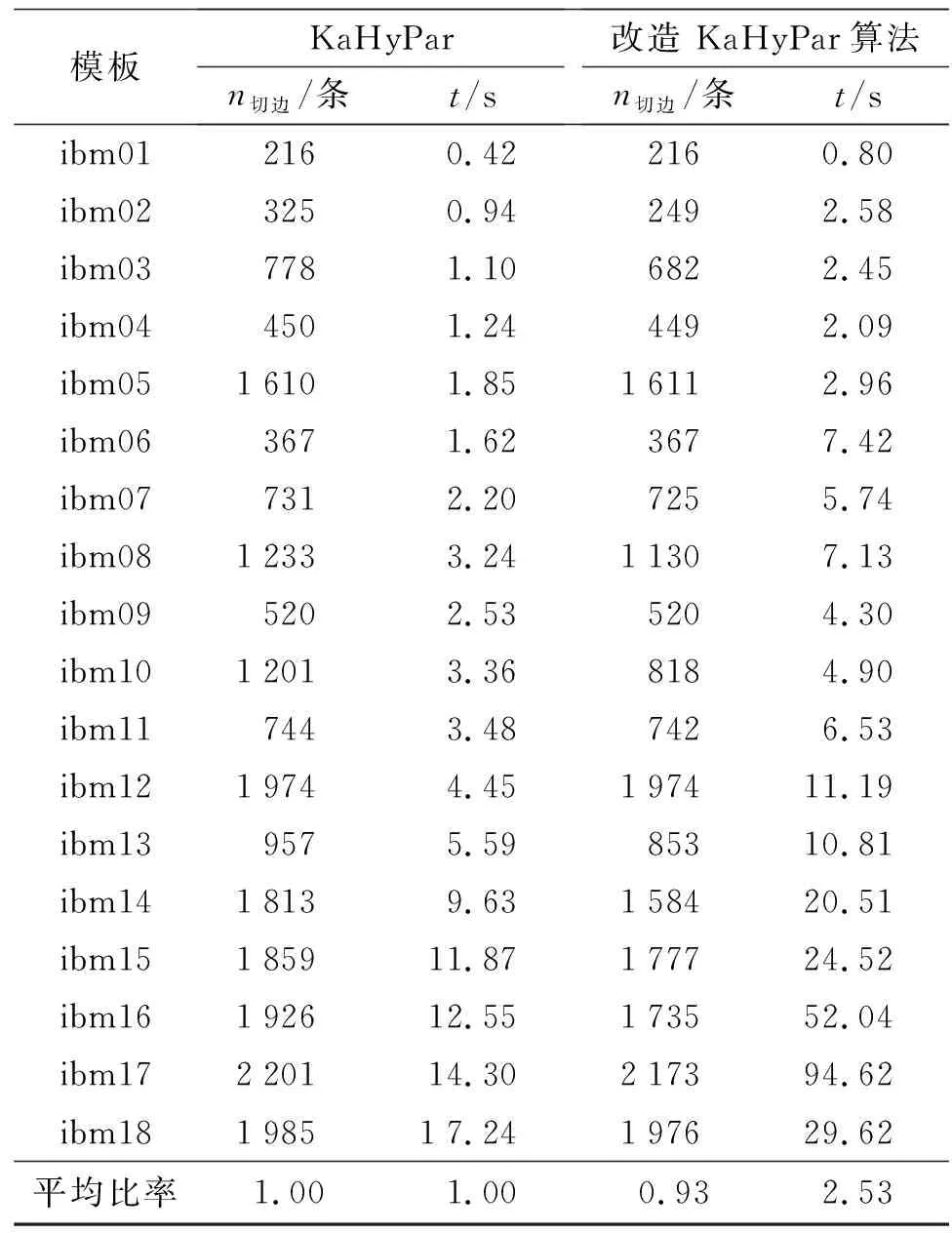
6: while ! is_balanced(x) andk

7: Nesterov_optimize(x)//使用Nesterov方法优化(使用预处理后的梯度)

9: end while

10: (V1,V2)=legalization(x)//根据坐标进行合法化得到划分

11: FM(G,V1,V2,ε)//使用FM算法进行局部优化

3 实验结果与分析

本研究采用ISPD98标准测试样例对所提出的非线性优化方法进行测试与分析. ISPD98标准测试样例中各个测试样例的数据说明详见参考文献[12]. 实验所涉及的算法均使用C++编译, 实验环境为CPU AMD Ryzen7 4 800 H, 8核, 主频2.9 GHz.

表1展示了本研究提出的二划分算法与加州大学圣地亚戈分校提供的FM算法开源代码直接对ISPD98标准测试样例进行划分得到的实验结果. 从表1可以看出, 本算法相较于FM算法在划分质量上有着十分显著的提升, 但运行时间却接近FM算法的10.5倍.

表1 与FM算法实验结果对比Tab.1 Comparison of results with FM

因此, 额外考虑将提出的算法嵌入到多级划分算法中的初始划分阶段, 得到Modified KaHyPar. 利用Modified KaHyPar和原始的KaHyPar进行实际的划分实验, 得到表2的实验结果. 从表2中观察到Modified KaHyPar对比于KaHyPar, 虽然在划分质量上的提升低于表1中与FM算法的对比, 但时间上的差距也大幅降低. 这两组实验均设置平衡参数ε=0.1, 运行时间的单位均为s, 最后一行平均比率表示对比项的平均比例.

表2 与KaHyPar实验结果对比Tab.2 Comparison of results with KaHyPar

4 结语

将二划分问题转化为一维离散布局问题, 并将其松弛为连续布局问题, 然后使用非线性优化方法求解, 将所得的连续解合法化后, 利用FM算法进行优化. 在ISPD98测试样例上的实验结果表明, 将多级划分算法KaHyPar的初始划分算法替换为上述算法较KaHyPar算法更有效. 在以后的研究中, 可以进一步考虑在连续优化过程中加入启发式方法以提升结果质量, 并通过改进数据结构、 程序逻辑与计算方法提升运行速度.