基于遗传算法的风力发电机叶片气弹阻尼优化*

□ 魏家星 □ 姜婷婷 □ 刘 勇 □ 宋佺珉 □ 端和平

浙江运达风电股份有限公司 风力发电技术重点实验室 杭州 311100

1 优化背景

近年来,随着风电行业竞争的日益激烈,为了提高竞争力和降低发电成本,风力发电机叶片大型化已成为发展趋势。风力发电机叶片在结构和气动方面表现出明显的非线性特征,气弹耦合作用容易引起风轮、主轴、塔架之间的振动,从而影响风力发电机的性能及稳定性[1]。

风力发电机气弹稳定性的评价主要是研究由叶片失速导致的气动负阻尼诱发叶片在摆振方向的振动失稳[2]。对于振动失稳发生机理已有学者进行了大量研究。黄鑫祥等[3]研究了叶片气弹失稳对整机性能的影响,发现叶片短暂失速会使叶片变形急剧增大,从而使风力发电机功率和载荷波动增大。Chen Chuan等[4]建立风力发电机转子运动方程,利用有限元方法求解,得到风力发电机在特定偏航角下产生气动负阻尼会导致叶片在摆振方向振动发散的结论。田德等[5]建立挥舞和摆振方向的叶片气弹阻尼计算程序,分析发现各阶模态气动阻尼为正值时,叶片运行稳定,反之,则容易产生失稳风险。由此可见,叶片气弹阻尼能够有效评估风力发电机的运行稳定性。当前叶片气弹阻尼的优化主要通过人工迭代的方式来调整叶片截面参数,比较耗时耗力,缺乏快速高效的优化工具。对于基于算法的风力发电机叶片优化,已经有大量学者进行了较为深入的研究。王珑[6]将叶片质量和发电量作为目标,利用进化遗传算法,优化叶片的结构和外形参数,实现叶片反向设计的程序开发。王永志等[7]将叶片的气动和结构性能作为约束,以质量为目标,采用多岛遗传算法,对风力发电机叶片进行优化设计,并对叶片的三维参数化模型进行分析,证明方法的有效性。

笔者借鉴叶片优化的设计方法,利用遗传算法对风力发电机叶片的结构参数进行寻优迭代,以快速准确优化叶片气弹阻尼,进而提高风力发电机叶片的优化效率。

2 叶片控制参数

作用于叶片展向叶素上的力由通过叶素扫过圆环的气流轴向动量变化率和角动量变化率产生[8]。每个叶素的截面性质是决定叶片载荷和稳定性的一个主要因素。在优化叶片气弹阻尼时,可通过调整叶片截面的结构参数来实现,即调整叶片铺层来改变截面刚度和剪切中心[9]。笔者以刚度变化量最小为目标,以摆振方向的阻尼值为约束,建立如下数学表达式:

F(x)=min{f1(x)+f2(x)+…+fn(x)}

(1)

式中:F(x)为目标函数;f1(x)～fn(x)为各截面参数变化量;n为截面数量;x为优化变量。

3 叶片参数化寻优

3.1 遗传算法

遗传算法是一种优化算法,通过基于优胜劣汰的选择策略和杂交变异操作,在随机生成的初始群体中寻找最优解。经过多代进化,种群逐渐趋向于最优解。相较于其它优化算法,遗传算法具有全局优化能力,可以避免陷入局部最优解,且寻优效率高。

3.2 叶片参数寻优过程

叶片参数寻优过程如图1所示,包括S1～S7共七个阶段。在S1阶段,设定截面优化范围,对每个截面给定一个刚度因子Ci,以a为初代叶片种群的个体数量。在S2阶段,针对每个个体,调用Bladed软件进行整机坎贝尔计算,将叶片刚度因子变化量ΔCi之和作为适应度,以阻尼为约束条件,ΔCi为|Ci-1|。在S3阶段,判断阻尼是否满足要求,通常要求一阶、二阶摆振方向的最小阻尼大于设定值,如果满足,执行S4,否则执行S7。在S4阶段,判断迭代是否收敛或完成,如果迭代次数小于最大迭代次数,那么执行S5,否则执行S6。在S5阶段,通过交叉和变异产生子代种群,将子代与父代合并形成新种群,个体数量为2a,然后对适应度进行排序,选出新子代种群,个体数量为a,执行S2。在S6阶段,输出寻优后的叶片刚度分布和阻尼值。在S7阶段,将未满足阻尼要求的个体适应度改为最大值,排除当前个体。叶片参数寻优过程能够实现自动化,避免工程师的经验试错,可以快速准确优化叶片气弹阻尼。

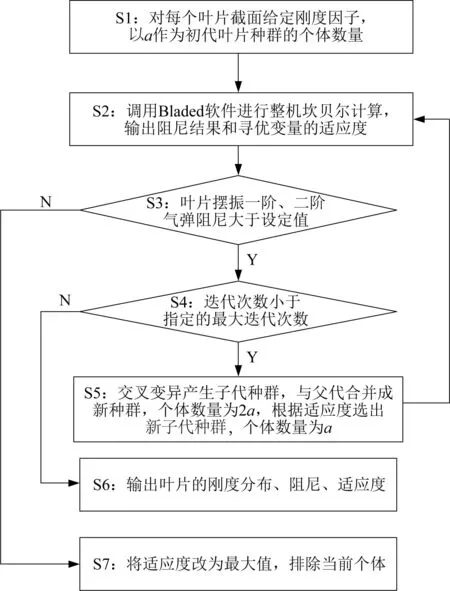
图1 叶片参数寻优过程

4 模型设置

根据需求准备计算模型和相关设置,寻优过程计算流程如图2所示,主要包括四个部分。

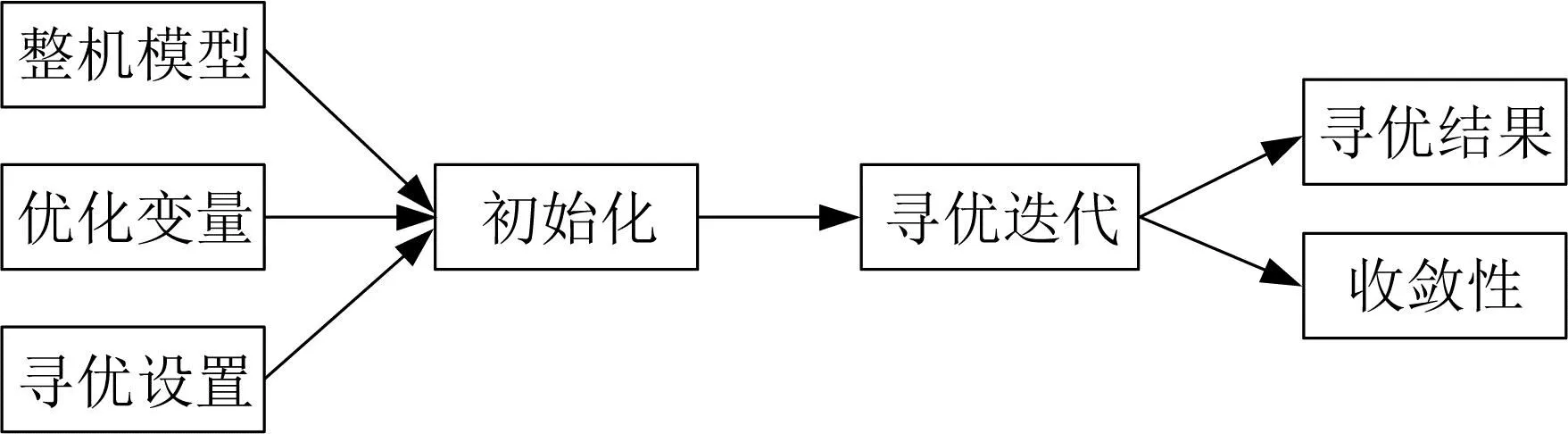
图2 寻优过程计算流程

(1) 模型设置。包括整机模型、优化变量、寻优设置。整机模型包括叶片、塔筒、机舱、传动链、控制文件等。优化变量通常为截面刚度和剪切中心,需要设置优化的截面范围和变量因子。寻优设置包括种群数量、寻优代数。其中,种群数量是每一代生成叶片的个体数量。

(2) 设置完成后开始进行初始化计算,程序会自动调用Bladed软件进行坎贝尔计算。通常初始化的个体数量较多,为后续寻优迭代提供基础种群。

(3) 每一代计算完成后,程序会输出最优的若干组解和适应度,以此来判断当前计算的收敛性。如果满足要求,可终止计算。

(4) 针对寻优结果,对比分析每个个体的可行性,选择最优的个体来进行后续结构和铺层的调整。

5 原有情况

某款叶片的几何模型如图3所示。在叶片设计与载荷迭代过程中,出现了载荷振荡的情况。

图3 叶片几何模型

通过坎贝尔分析发现,在11～15 m/s风速下均出现摆振方向的负阻尼,叶片气弹阻尼见表1,这是导致叶片载荷振荡的主要原因之一。其中,最小的负阻尼为一阶总体摆振方向的-0.055 7,较为严重,极易引起叶片载荷振荡。对此,采用遗传算法优化叶片扭转刚度,来提高叶片气弹阻尼。

表1 叶片气弹阻尼

6 气弹阻尼寻优计算

为了优化叶片气弹阻尼,并且不影响载荷的迭代结果,需要尽可能小改变叶片结构参数来消除负阻尼,精准控制叶片结构参数。由此,以叶片刚度变化量最小为寻优目标,要求叶片一阶、二阶摆振方向的气弹阻尼大于0。优化变量为叶片扭转刚度,截面位置范围为30～80 m,截面刚度因数范围为0.95～1.2。种群数量为60,寻优代数为30,寻优总耗时约48 h。

叶片气弹阻尼寻优结果见表2。通过寻优迭代,叶片在11～15 m/s风速下的气弹阻尼均大于0,最小值为风速11 m/s时二阶总体摆振方向的0.004 8,由此提高了风力发电机的运行稳定性。

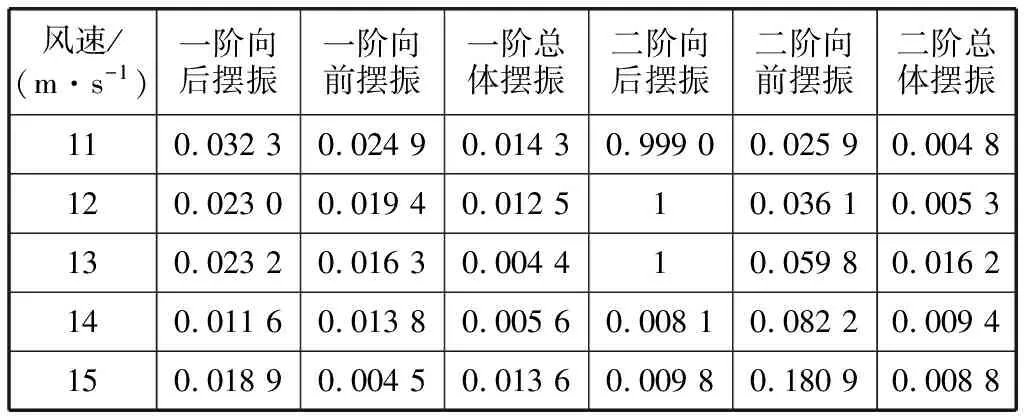
表2 叶片气弹阻尼寻优结果

7 叶片扭转刚度分布

寻优前后扭转刚度分布曲线如图4所示。分析发现,影响叶片气弹阻尼的敏感截面主要集中在31 m、37 m、40 m处。特别是在31 m处,原情况的扭转刚度相对较弱,需要在该处重点加强。此外,观察曲线还可以发现,有些截面的扭转刚度是需要降低的,如34 m、43 m处。这说明截面刚度并不一定是越大越好,有时候适当降低某一截面的扭转刚度,反而可以更有利于叶片的稳定性。由此可见,叶片的参数设计是一个综合考量的结果,通过合理的参数匹配才能设计出高性能、高可靠性的叶片。

图4 寻优前后扭转刚度分布曲线

8 叶片铺层优化

基于寻优后的扭转刚度分布曲线,设计时在30～80 m截面范围内进行结构铺层调整,针对扭转刚度主要调整双轴布铺层,使铺层后的刚度分布能够包络且尽可能靠近寻优曲线[10]。铺层前后扭转刚度分布曲线如图5所示,铺层后的扭转刚度分布可以覆盖寻优曲线,但在43 m、46 m处差距较大,这是由于铺层连续性造成未能精准控制所有截面刚度变化的原因。最终,经过铺层后,叶片在11～15 m/s风速下的气弹阻尼均大于0。叶片气弹阻尼铺层结果见表3,最小值为12 m/s风速时二阶总体摆振方向的0.004 1。由此证明了遗传算法在优化叶片气弹阻尼方面的实际效果,可以提高叶片的设计和优化效率。

表3 叶片气弹阻尼铺层结果

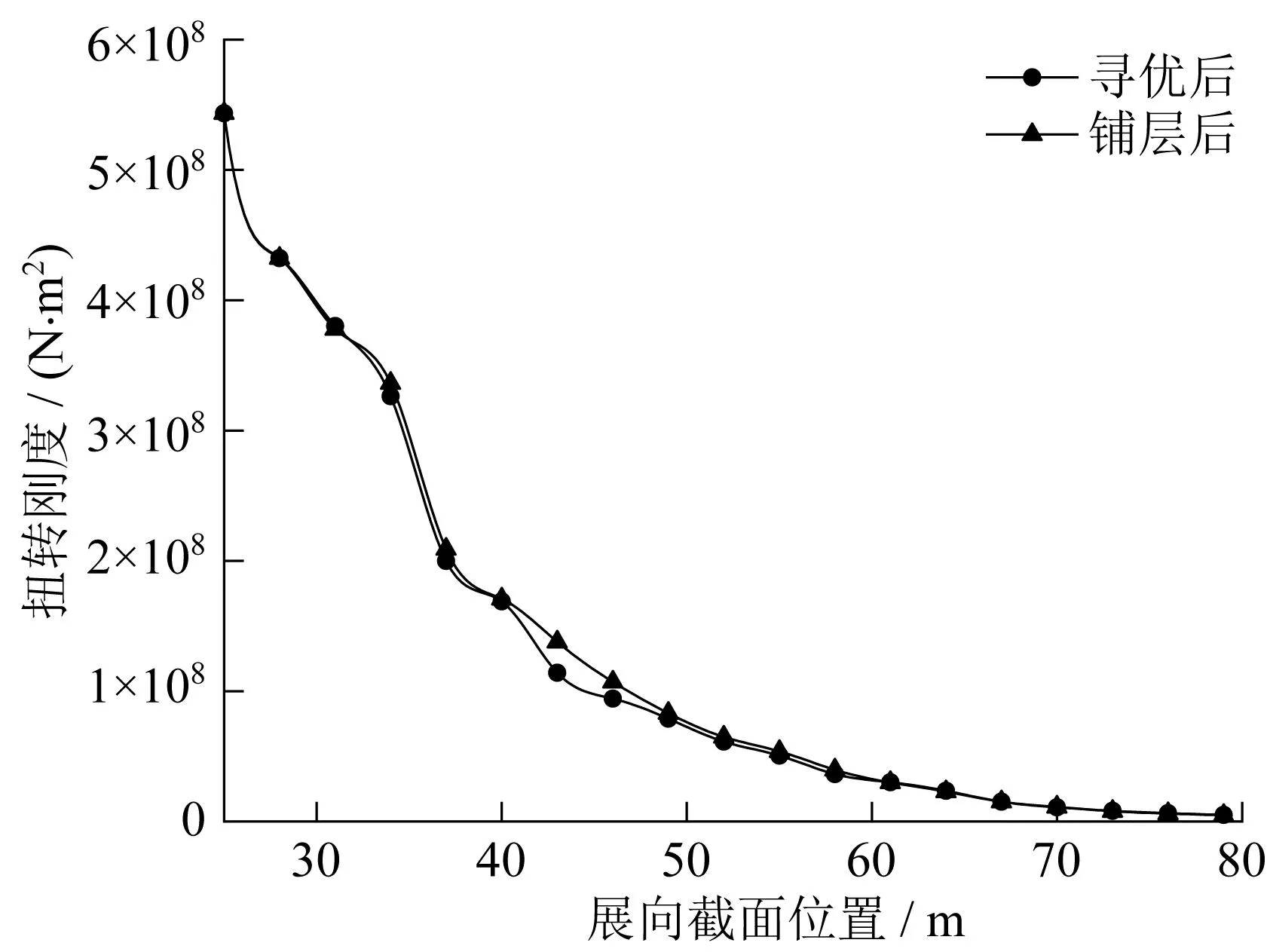
图5 铺层前后扭转刚度分布曲线

9 结束语

为了高效优化叶片气弹阻尼,采用遗传算法对叶片扭转刚度进行迭代寻优,以确定影响叶片气弹阻尼的敏感截面。根据寻优曲线,调整叶片结构铺层,使优化后的刚度分布包络寻优曲线,从而提高叶片气弹阻尼的优化效率。结果表明,通过遗传算法能够快速、准确地找到影响叶片气弹阻尼的敏感截面,实现叶片结构参数的精细化设计,从而优化叶片气弹阻尼。笔者的研究成果可以为风力发电机叶片的设计和优化提供有力支持。