撒砂装置振动疲劳寿命评估研究
邹洪伟,苑红磊,吴兴文,吕晓鹏
(1.中车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.西南交通大学 机械工程学院,四川 成都 610031)
随着我国动车组运营里程和年限的增加,附属结构的安全可靠性变得更为重要[1]。撒砂装置在防止车轮空转滑行尤其是在恶劣天气条件下保证列车平稳运行起重要作用[2],撒砂装置的撒砂器(以下简称“撒砂装置”)由于安装在轨道正上方,因此保证其在服役情况下不出现结构失效是关注的重点。早期针对转向架部件的疲劳强度设计主要基于EN/UIC/JIS等标准的准静态方法对结构疲劳强度进行校核,该方法主要利用多个极限工况校核结构关键位置的应力是否超出结构的许用应力,并利用无限寿命设计准则对结构作出评价,这种方法不考虑载荷频率的影响。但由于多种不平顺激励加之车辆运行速度的提高,经过准静态疲劳校核后的撒砂装置会出现因随机振动疲劳而导致结构失效的现象(包括螺栓失效和结构裂纹等),对列车的安全运营带来了极大的影响。基于此,通过开展转向架撒砂装置振动疲劳研究以预测撒砂装置的使用寿命,并据此对撒砂装置进行更换和维护,对保证车辆的安全运行具有重要意义。
20世纪60年代,CRANDALL[3]首次将随机振动理论应用于结构疲劳研究中,并和MARK[4]对振动疲劳作出了定义,即结构在振动载荷激励下产生的具有不可逆、累积性的损伤或者破坏叫作振动疲劳。1975年,姚起杭等[5]给出了共振疲劳的定义,并指出了疲劳问题应该分为结构静态疲劳和动态疲劳,不应将二者统一考虑。王明珠[6]研究了不同频率加载对金属材料抗疲劳性能的影响,提出了该金属材料的S-N曲线模型,并研究了不同阻尼系数、应力集中和平均应力对结构疲劳寿命的影响,给出了应力集中下缺口件的振动疲劳寿命评估方法。白金等[7]考虑结构随机振动下的多轴应力状态与共振对疲劳寿命的影响,引入了新的随机振动疲劳损伤参量,建立了一种新的随机振动疲劳寿命预测方法,并对其预测准确性进行了研究。张勇等[8]以转向架构架为研究对象,考虑其柔性建立了机车刚柔耦合动力学模型,结合疲劳极限定理校核了构架的疲劳强度,得出了构架满足疲劳要求的结论。
轮对和钢轨传递来的高频载荷往往会激起撒砂装置结构的高频模态共振[2],而准静态疲劳评估方法没有考虑高频载荷对结构的影响,故对撒砂装置等受载复杂结构的疲劳强度评估存在局限性。准确描述撒砂装置载荷特征是对其进行疲劳寿命评估的关键,因此,本文结合轴箱线路实测加速度信号,研究了撒砂装置振动服役环境,考虑了结构模态共振对结构振动疲劳的影响,并对基于标准IEC 61373:2010《铁路应用 机车车辆设备 冲击和振动试验》定义的振动功率谱与基于实测数据得到的功率谱作为激励进行了对比,采用不同方法对撒砂装置的疲劳强度进行了评估,以期找到更为合适的振动疲劳评估方法,为寿命评估奠定基础。
1 撒砂装置结构介绍
撒砂装置是为了改善轮轨黏着而设计的装置,能够通过控制箱将砂箱中的石英砂通过管道喷射在钢轨上,从而提高车轮与轨道间的黏着系数,起到防止车轮滑行的作用。高速动车组每列车通常安装8套撒砂装置,撒砂装置由砂箱、撒砂单元、控制箱、撒砂器(包括安装臂、托架和撒砂加热器)等组成(图1),在列车高速运行过程中,撒砂器通过轴箱承受来自轮轨的高频振动。本文主要针对安装臂进行研究,如图1中红色边框所示。

图1 撒砂装置示意图
为了准确再现撒砂装置服役振动环境,并较为准确地计算出撒砂装置部件在关键位置的振动响应,进而对撒砂装置疲劳寿命进行合理评估,本文建立了基于虚拟激励法的撒砂装置随机振动模型。模型建立的关键技术包括2个方面:基于实测轴箱振动的虚拟激励实现和撒砂装置刚柔耦合动力学模型的建立。
结合虚拟激励法建立的撒砂装置试验台仿真模型通过PID控制能够再现撒砂装置试验振动环境,然后根据模态应力恢复法求解撒砂装置关键位置的应力动态响应,通过与试验台实测动应力结果对比来调整模型参数,使其具有较好的一致性,从而验证了基于虚拟激励法的撒砂装置随机振动建模方法的正确性。
2 疲劳寿命评估方法
现阶段结构寿命评估方法主要分为2种:时域法和频域法,二者具有互相不可替代的优势。时域法虽然能够比较准确地预测结构的寿命,但是对于诸如撒砂装置这样受载复杂的结构,因其承受的外部激励往往是复杂多变的随机信号,因此欲对其结构寿命作出准确评估,需要足够长的时域载荷数据,在这样的情况下必将加大计算量。随机信号虽然在时域情况下是变化的,但在频域情况下具有不变的特性,利用更少的数据表示信号特征,由此提出了很多不同的频域疲劳寿命评估方法,可以极大地提高计算效率。
2.1 时域法
通过时域法对结构进行疲劳寿命评估,首先确定研究对象的时域载荷,并结合有限元法计算求得结构关键位置的应力-时间历程。随后利用循环计数方法将得到的应力-时间历程的应力幅值和对应的循环次数进行统计。最后根据结构的材料属性选取合适的S-N曲线,并结合Miner线性累积损伤准则计算出关键位置的损伤,再结合实际情况定义适当的损伤阈值,进而对结构的疲劳寿命进行预测。
2.2 频域法
利用频域法对结构的疲劳寿命进行评估,首先需要根据载荷-时间历程经过傅里叶变换求得载荷功率谱,通过频响分析得到结构关键位置的应力功率谱,再结合不同频域疲劳评估方法求得应力范围概率密度函数,最后利用S-N曲线以及Miner线性累积损伤准则求得在规定时间内的结构损伤。针对文中的轴箱振动加速度、撒砂装置关键位置的动态应力响应等随机信号,不能根据之前已经发生的信号来预测下一时刻的瞬时幅值,只能利用统计方法对其进行描述[9-10]。
3 基于标准振动谱的寿命评估
3.1 激励信号验证
根据标准IEC 61373:2010对轴装振动载荷谱定义的功能测试试验部分,纵向、横向、垂向3个方向的ASD量级分别为8.74 (m/s2)2/Hz、7.0 (m/s2)2/Hz、1.751 (m/s2)2/Hz。以垂向为例,根据垂向加速度功率谱通过傅里叶逆变换得到时域加速度信号,如图2所示。经计算后的加速度信号幅值在±150 m/s2范围内波动,为了验证该加速度时域信号满足标准IEC 61373:2010要求,再次将该时域信号经傅里叶变换得到对应的目标加速度功率谱,并与标准对比,结果如图3所示。由图3可知,目标信号的加速度功率密度曲线处于标准信号的上下限内,二者具有良好的一致性。通过PID控制策略使轴箱按照前面得到的加速度时域信号进行振动,轴箱的实际信号与目标信号具有较好的一致性,满足标准IEC 61373:2010对轴装部件载荷环境的要求。
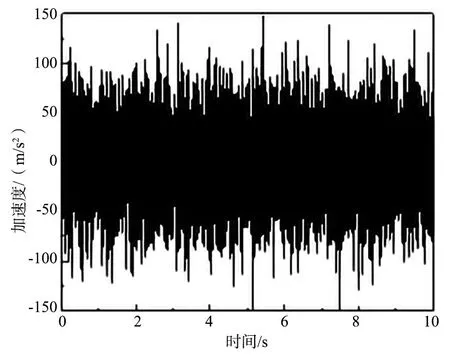
图2 轴装部件垂向加速度时域信号

图3 仿真加速度信号与标准加速度信号对比
3.2 应力响应频率分析
对建立好的模型进行时域积分,仿真10 s得到撒砂装置关键位置的动态应力响应,如图4所示。对应力-时间历程进行傅里叶变换得到应力功率谱,如图5所示。由图5可知,应力信号的主频为13.7 Hz、132.8 Hz、464.8 Hz,其中,132.8 Hz附近的能量占大部分能量,但464.8 Hz附近的加速度功率谱幅值较小,10~200 Hz范围的加速度功率谱幅值较大。

图4 撒砂装置关键位置应力-时间历程

图5 撒砂装置关键位置应力功率谱
3.3 时域法与频域法结果对比
对得到的应力-时间历程进行雨流计数处理得到应力范围和对应的循环次数,统计出不同应力范围下的概率密度,结合Dirlik法、Lalanne法、Rayleigh法和Zhao-Baker法分别对应力范围概率密度进行拟合[11-13],各个方向拟合结果如图6所示。由图6可知,撒砂装置按照标准IEC 61373:2010纵向、横向、垂向3个方向振动功率谱进行振动,撒砂装置关键位置的应力范围主要为小幅值。在4种不同疲劳频域分析方法的拟合情况中,Zhao-Baker法和Dirlik法均能较为准确地与时域法结果拟合,其中,Dirlik法对小幅值应力范围的描述明显优于Zhao-Baker法,另外2种方法对实际结果的描述误差较大。

图6 各方向应力范围概率密度及其拟合情况
根据雨流计数法得到的应力范围和对应的循环次数,结合S-N曲线和Miner线性累积损伤准则得到纵向、横向、垂向3个方向历时1 h的结构累积损伤,如表1所示。由表1可知,在4种频域法计算结果中,Zhao-Baker法和Dirlik法与时域法的计算结果较为接近,而Lalanne法和Rayleigh法相差较大,说明Zhao-Baker法和Dirlik法对撒砂装置结构损伤计算较为准确,可以将该方法应用于周期性载荷的撒砂装置随机振动疲劳研究中。

表1 不同方法损伤计算结果
4 基于实测数据的寿命评估
4.1 实测数据功率谱统计
基于线路实测数据对撒砂装置的振动功率谱进行研究,得到不同运营里程下的加速度功率谱,其均值水平和99.85分位数情况如图7所示。
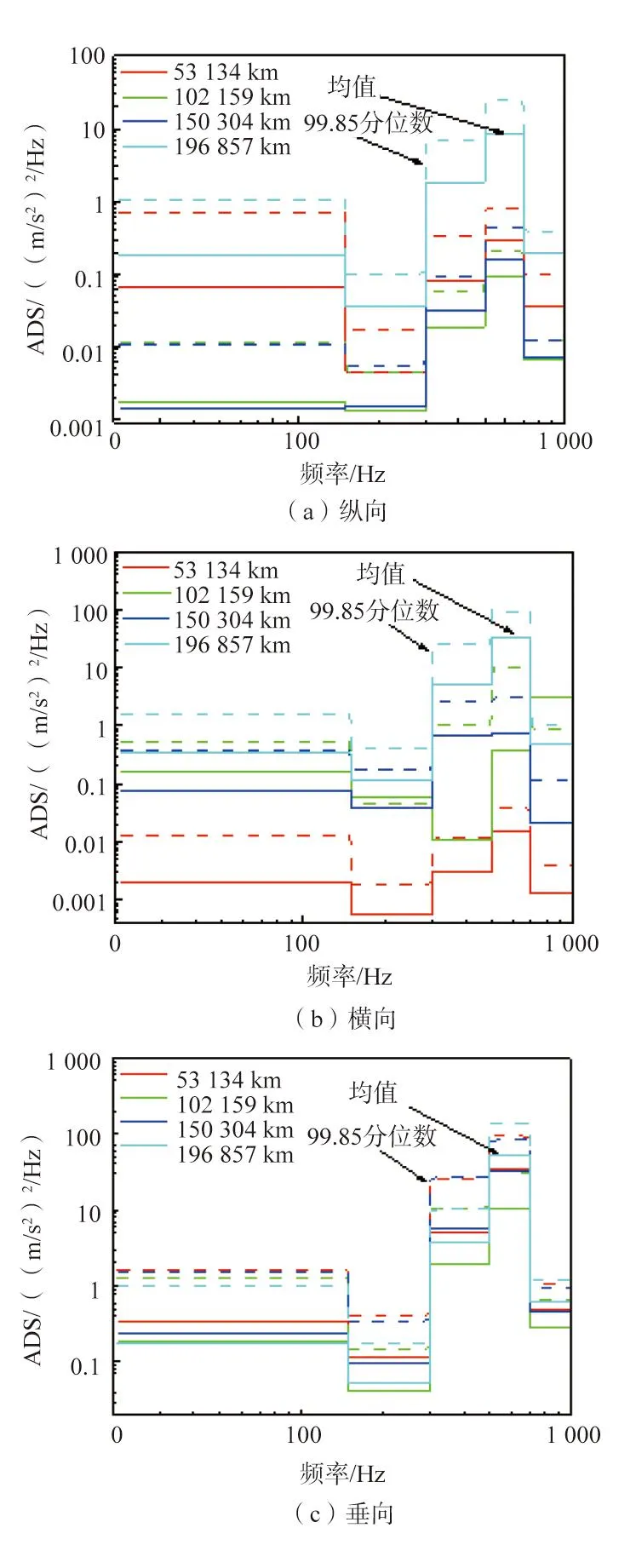
图7 撒砂装置疲劳寿命评估输入载荷
4.2 实测数据应力响应频率分析
根据图7中3个方向不同里程的加速度功率谱作为撒砂装置载荷输入进行疲劳寿命评估,通过模态应力恢复法得到撒砂装置关键位置的应力响应。将垂向载荷应力-时间历程经过傅里叶变换得到对应的应力功率谱进行展示,不同运营里程下撒砂装置关键位置的应力功率谱曲线如图8所示。由图8可知,所有功率谱的主频均为464.8 Hz,且该频率附近的频率范围占整体大部分能量,虽然与标准结果中的其中一个主频一致,但在能量分布和能量幅值上均出现较大差异。而且标准IEC 61373:2010没有考虑频率范围500~700 Hz,表明标准中定义的撒砂装置振动功率谱高估了20~300 Hz频率范围的撒砂装置服役载荷幅值水平,低估了300~500 Hz的载荷幅值并忽略了500~700 Hz频率范围对撒砂装置疲劳强度的影响。同时,在撒砂装置的结构设计阶段,需要重点考虑464.8 Hz附近的振动模态。

图8 垂向载荷情况下撒砂装置关键位置应力功率谱对比
4.3 时域法与频域法结果对比
对垂向载荷不同里程的响应结果利用雨流计数求得应力范围和对应循环次数,经过统计得到不同里程的应力概率密度,并结合不同的频域疲劳寿命评估法对应力范围概率密度进行估计,结果如图9所示。由图9可知,Dirlik法和Zhao-Baker法对实际应力概率密度的估计情况同样明显优于Lalanne法、Rayleigh法。

图9 撒砂装置关键位置应力范围概率密度拟合情况
根据应力范围概率密度结果,结合Miner线性累积损伤准则和S-N曲线,得到不同疲劳寿命评估方法计算的1 h内损伤计算结果,如表2所示。Dirlik法和Zhao-Baker法损伤计算结果与时域法计算结果较为接近,表明这2种方法均能够较为准确地计算结构损伤。

表2 垂向载荷情况下1 h内损伤计算结果
5 结论
(1) 针对撒砂装置结构损伤的计算,本文比较了4种不同的频域法,计算结果表明Zhao-Baker法和Dirlik法是较为准确的。
(2) 基于实测数据得到的应力功率谱的主频为464.8 Hz,且该频率附近的频率范围占整体大部分能量,与标准结果中的其中一个主频一致,但二者在幅值和能量分布上均具有较大的差异。标准IEC 61373:2010没有考虑频率范围500~700 Hz,而实测数据中此频率段的能量是不能忽略的,且存在高于20~300 Hz能量的情况。表明标准IEC 61373:2010中定义的功率谱高估了20~300 Hz频率范围的撒砂装置服役载荷幅值水平,而忽略了500~700 Hz频率范围对撒砂装置疲劳强度的影响。

