多边形条件下高铁车轴裂纹扩展寿命计算及检查间隔制定方法研究

吴聪瑞,邬平波,刘潮涛

(西南交通大学 轨道交通运载系统全国重点实验室,四川 成都 610031)

1 概述

车轴是铁道车辆的关键部件,车轴疲劳失效往往会导致灾难性的后果。欧洲发生过多起车轴断裂事故[1-3](图1),严重威胁车辆的运行安全。在实际运用过程中,车轴常受到异物冲击或者被划伤,此时基于安全寿命设计的前提不再成立。损伤车轴的剩余寿命一般采用损伤容限法进行评估,近年来国内外多位学者针对这一问题进行了广泛研究,秦庆斌等[4]在考虑了车轴残余压应力的基础上,分别基于Paris方程和NASGRO方程预测了S38C空心车轴的剩余寿命;王文洁[5]在考虑二次应力的条件下,利用NASGRO方程预测了动车车轴2 mm初始裂纹的裂纹扩展寿命,并分析了裂纹形状、深度等对裂纹扩展行为的影响;POKORNY[6]进行了车轴剩余寿命的仿真计算,研究了不同载荷对剩余寿命的影响,包括载荷离散水平等。

图1 车轴断裂

对于车轴危险截面的选取,根据ICE3在实际应用过程中轮座内侧发生疲劳断裂的情况[7],选择轮座和轴身间75 mm圆弧和15 mm圆弧的过渡截面作为危险截面的位置与很多学者的研究成果相同。刘宇轩[8]对EA4T材料的轴箱内置和轴箱外置动力车轴分别进行了有限元仿真,得到了车轴轴向应力场分布,发现内置轴箱车轴临界安全截面位于轴身中部,外置轴箱车轴临界安全部位位于车轮座和齿轮座之间的卸荷槽处;POKORNY 等[9]考虑残余应力和载荷谱的综合作用,对于EA4T动力车轴选择轮座和驱动车轮座间的“S”型过渡区域作为危险截面;NHLK 等[10]采用有限元方法计算了EA4T车轴轴向应力沿车轴长度方向的应力分布,选择轮座和轴身间的“T”型过渡区域作为危险截面。由此可见,从车轴实际应用情况和很多学者的研究成果得出,危险截面应选择轮座和轴身间的卸荷槽部位。

此外目前广泛采用的确定性方法确定车轴检查间隔往往会得到过于保守的结果,车轴合理检查间隔的制定一直面临着巨大的考验[11]。GIANNELLA[12]在考虑材料属性、载荷条件和裂纹扩展公式中计算参数随机性的条件下,提出了一种预测车轴剩余寿命的随机性的方法。AKAMA[13]在假设车轴疲劳寿命服从三参数的威布尔分布的条件下,利用蒙特卡洛方法来随机地获取门槛应力强度因子范围ΔKtΔ和常数C。相似地,在文献[14-15]中,ΔKth0和 logC作为2个独立的随机变量,同时服从正态分布。由此可见,对于材料属性本身的离散性,大多反映在裂纹扩展方程参数的分布形式,而且对于分布形式并没有得到统一的结论。

关于铁道车辆构架应力谱的分布已有大量研究,但很少有关于车轴应力谱分布方面的研究以及考虑载荷离散性条件下的车轴寿命的评估方法研究。牛留斌[16]以车轴卸荷槽为研究对象,通过全程实测所得的车轴应变数据来编制应力谱,基于确定性断裂力学计算车轴剩余寿命。金新灿等[17]通过标定试验和线路实测试验,编制了中国标准动车组测力轮对的载荷谱,并以最恶劣工况的载荷谱作为输入载荷,用于计算裂纹扩展到临界尺寸时的剩余寿命。徐忠伟等[18]基于线弹性断裂力学理论和塑性致裂纹闭合效应,利用实测动应力分别在车轴5个部位植入半椭圆形裂纹,计算其剩余寿命。由此可见,对于载荷条件的考虑,多是基于线路实测的载荷谱,但由于实测载荷谱样本数量较少,对载荷离散性无法进行定量的分析。

本文将针对某型动车组动力车轴轮座和轴身间的卸荷槽部位裂纹,采用动力学仿真的方法在车轮多边形条件下提取危险截面的应力谱;利用小试样裂纹扩展试验数据来拟合NASGRO方程参数,然后对车轴剩余寿命进行评估;在考虑了车轴材料属性离散性、载荷条件离散性后,确定车轴剩余寿命的安全系数;最后,根据空心车轴目标失效概率和裂纹检出概率曲线来制定车轴的检查间隔,以期为损伤车轴剩余寿命评价和检查间隔的制定提供指导。车轴检查间隔制定技术路线如图2所示。

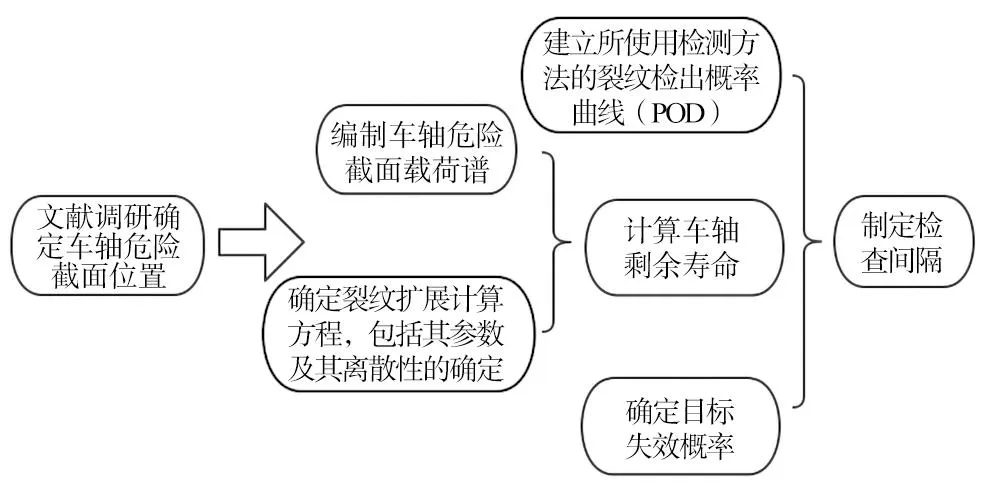
图2 车轴检查间隔制定技术路线

2 基于动力学仿真分析的车轴应力谱编制

2.1 刚柔耦合动力学模型的建立

在建立车辆刚柔耦合动力学模型之前,首先采用缩减矩阵法缩减轮对模型的自由度,建立轮对柔性体,以此提取在不同工况条件下车轴危险截面的随机应力谱。在导入轮对柔性体之前,首先对轮对进行自由模态分析,采用SOLID186单元来建立轮对的有限元模型,其有限元模型如图3所示。然后,利用ANSYS软件中的Block Lanczos方法进行轮对自由模态分析,分析轮对前20阶模态,其部分振型和频率如图4所示。

图3 轮对有限元模型

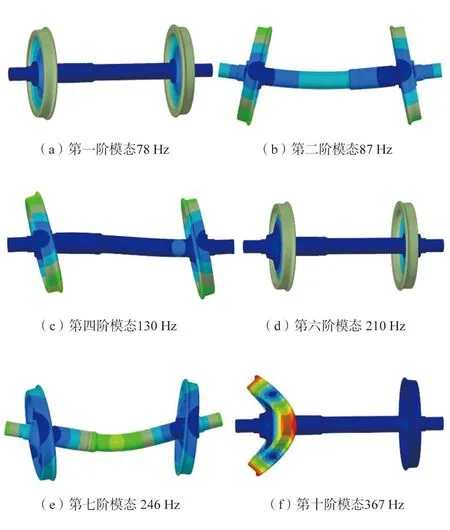
图4 轮对模态振型及频率

本文利用SIMPACK软件建立了包含2个构架、1个车体、8个轴箱和4条轮对的多刚体动力学模型。一系为转臂式结构并安装有一系垂向减振器和钢弹簧;二系安装有抗蛇行减振器、空气弹簧、抗侧滚扭杆、二系垂向减振器和二系横向减振器等。动力学模型如图5所示。自由度如表1所示,轴箱只考虑了点头自由度。

表1 车辆系统动力学模型自由度

图5 车辆系统多刚体动力学模型

2.2 危险截面不同工况下动应力特征分析

载荷谱工况是根据京沪线一次往返行程中车辆运行速度、曲线半径和里程占比来划分的,一次往返里程总共2 636 km。利用SIMPACK软件分别提取20阶车轮多边形、0.05 mm波深条件下17个工况危险截面10 s的随机应力谱。图6截取了曲线半径为800 m、2 200 m时车轴危险截面应力变化曲线,并分别对每个工况的应力进行了时频域分析。

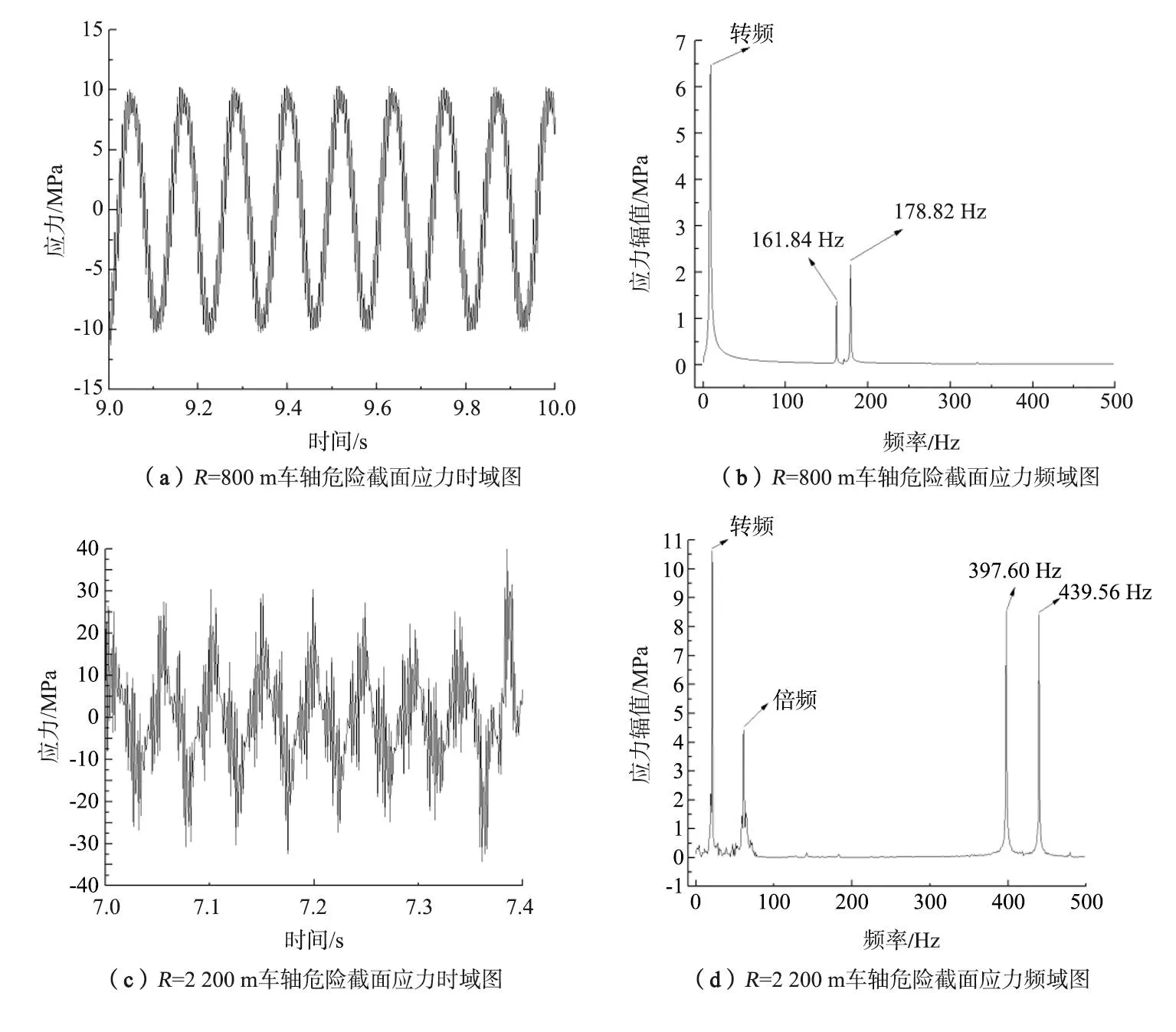
图6 部分仿真工况车轴应力时域及频域图

从图6中可以看出,多边形条件下车轴的总应力为车辆静轴重产生的旋转弯曲应力叠加多边形产生的一定的幅值应力,不同工况下车轮多边形产生的应力幅值不同。从2个工况的车轴危险截面应力频域图中可以看出,车轴应力主频为车轴的转频。在R=800 m时,在161.84 Hz和178.82 Hz多边形激励频率附近有明显的幅值,幅值分别为1.5 MPa和2 MPa左右;在R=2 200 m时,车轴应力主要的频率成分为转频及其倍频,而397.60 Hz和439.56 Hz与轮对的结构模态接近,2个频率下车轴应力幅值均达到了8 MPa以上,模态振型如图7所示。由此可见,某些工况下,车轮多边形会激发轮对的高阶模态,进而增加车轴危险截面的应力,影响车轴的疲劳寿命。

图7 轮对结构模态

2.3 车轴危险截面应力谱的编制

通过动力学仿真获得各工况下的车轴应力-时间历程之后,通过雨流计数法进行统计归纳,在平均应力为0 MPa时,按照“低-高-低”的加载顺序编制的块谱计算得到的疲劳寿命与实际工况下随机载荷计算结果相似[19]。

为了简化载荷谱,对裂纹扩展门槛值以下的载荷进行小载荷省略,其计算方法如下:在裂纹尺寸为临界失效尺寸时,应力比R=-1条件下,计算在该裂纹深度下的应力强度因子范围,舍去此时应力强度因子范围小于应力强度因子门槛值的小载荷。应力强度因子范围计算公式如下[20]:

(1)

式中:ΔK为应力强度因子范围;Y为形状因子,其取值参考文献[21];Δσ为应力范围,在R=-1条件下,Δσ=2σmax;a为裂纹长度。

车轴临界失效尺寸指的是在指定载荷条件下,不发生脆性断裂的最大裂纹尺寸[22]。由此可得:

(2)

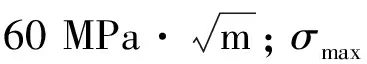
计算得到车轴临界失效尺寸为40 mm,某条线路下的车轴危险截面应力谱如图8所示。

图8 车轴危险截面应力谱

3 裂纹扩展寿命计算

3.1 裂纹扩展模型

Paris、Walker和Forman是最常用的裂纹扩展计算方程。相比之下,由Forman发展而来的NASGRO方程更适用于实际情况下的裂纹扩展计算。王文洁[9]针对变幅载荷条件,利用车轴M(T)试样的疲劳裂纹扩展试验对比了Paris和NASGRO方程车轴剩余寿命计算结果,结果表明NASGRO方程的寿命预测结果更加准确。

对于铁路车轴来说,NASGRO方程及其修正后的版本已经在裂纹扩展计算方面得到了广泛应用[23-25]。因此,本文将采用NASGRO方程进行裂纹扩展的仿真计算。NASGRO方程使用有效应力强度因子范围来考虑塑性致裂纹闭合效应和应力比对裂纹扩展的影响[26],方程表达式如下:

(3)

(4)

(5)

A1=(0.415-0.071α)σmax/σ0

(6)

A3=2A0-A1-1

(7)

A2=1-A0-A1-A3

(8)

公式(3)为裂纹扩展速率和应力强度因子范围 ΔK的表达式。NASGRO理论手册[27]中有关于方程的详细介绍。α为约束因子,在平面应变条件下,一般取α=3,σmax/σ0=0.25。公式(3)中,(1-Kmax/Kc)q表示裂纹扩展的瞬断区,由于在该区域裂纹扩展较快,在裂纹扩展的寿命当中占比很小,所以本文省去了该项,取q=0[28]。方程中主要的参数包括C、m、p和ΔKth,均由试验数据拟合而来。ΔKth为裂纹扩展的门槛值,其计算方法见NASGRO理论手册。f被称为Newman’s closure function,表征裂纹闭合效应。

3.2 模型参数的试验数据拟合

表2为使用Levenberg-Marquardt 优化算法对公式(3)拟合得到的方程参数的中值,该组参数将用于计算车轴剩余寿命的中值。图9为文献[29]中由EA4T车轴小试样试验得到的应力比R=-1条件下的裂纹扩展试验数据。

表2 应力比R=-1时NASGRO参数中值拟合

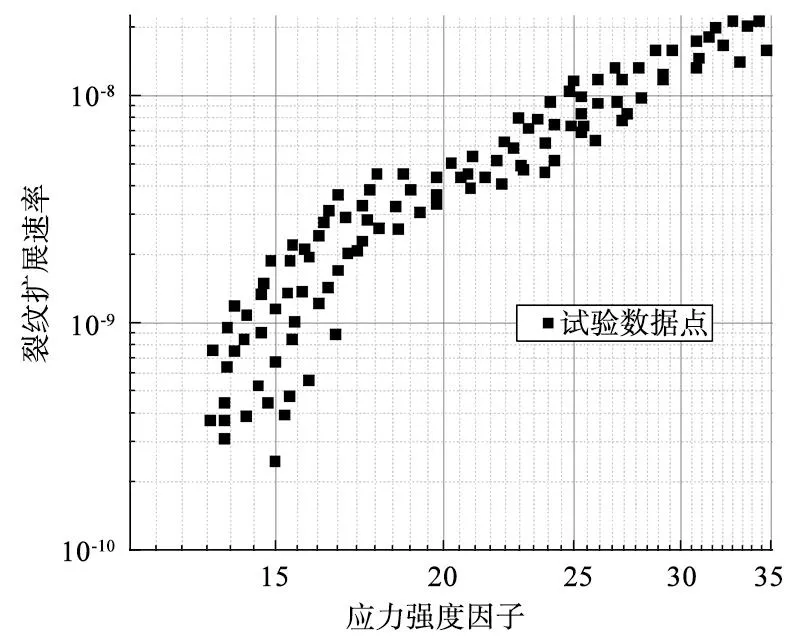
图9 EA4T车轴试样裂纹扩展试验数据

3.3 车轴有限元模型及剩余寿命计算结果

带有初始裂纹的EA4T车轴的有限元模型如图10所示。为了提高计算效率,省去了无裂纹侧的车轮,不考虑车轮和齿轮箱压装导致的残余应力。三维四面体单元为SOLID186,裂纹尖端为15节点奇异楔形单元,楔形单元和四面体单元之间采用20节点六面体单元平滑过渡。基于无损检测的最高精度为2 mm,初始裂纹深度选择为a0=2 mm,裂纹形状为半椭圆形,长度2c0=5 mm,初始裂纹深度和半长度比值a0/c0=0.8。

图10 带有半椭圆形裂纹的车轴有限元模型

边界条件施加如下:约束车轮踏面3个方向的位移和转动,载荷P施加在齿轮箱侧的轴颈上,并根据所编制应力谱改变其幅值,达到类似悬臂梁结构下车轴的反向弯曲。在只考虑Ⅰ型裂纹扩展的情况下,仿真采用M-积分来计算应力强度因子。弹性模量E=2×105MPa,泊松比v=0.3。

仿真计算时车轴危险截面应力的实现需要靠齿轮箱侧轴颈所施加的垂向载荷P,因此,需要进行车轴静态下的载荷标定。在无裂纹情况下,按照上述加载方式,在载荷大小为10 kN的情况下,通过仿真计算,危险截面的应力为37.581 MPa,如图11所示。

图11 无压装条件下车轴应力分布

使用第2节中得到的应力块谱和第3节中NASGRO方程及其参数拟合结果,计算裂纹深度从2 mm到40 mm的车轴剩余寿命的中值,为下文安全系数的确定和检查间隔的制定提供计算依据。

使用表2中NASGRO方程参数中值进行车轴剩余寿命计算,得到车轴的中值寿命N50=1.06e+08cycle≈38.5万km,其裂纹扩展曲线如图12所示。因此,在20阶车轮多边形、0.05 mm波深条件下,使用NASGRO方程参数中值计算得到的裂纹从2～40 mm的车轴剩余寿命为38.5万km。

图12 车轴剩余寿命中值曲线

4 车轴剩余寿命可靠性研究

4.1 材料属性

由于材料微观结构的不规则性、生产加工过程的差异等,裂纹的萌生和扩展本质上是一个随机的过程[30]。

表3 应力比R=-1时,ΔKth,R=-1和log10C分布参数拟合结果

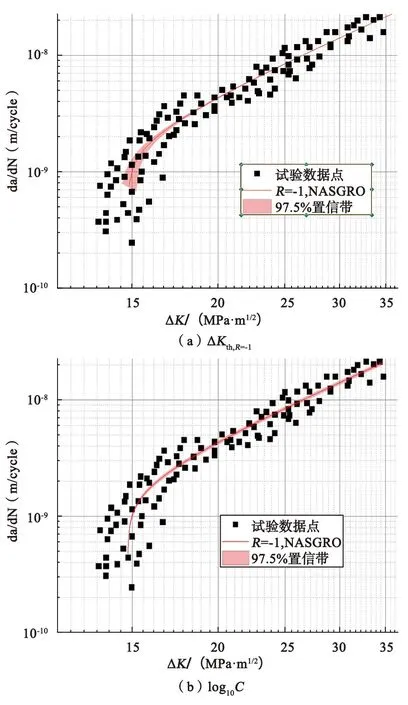
图13 裂纹扩展数据97.5%置信带(R=-1)

各剩余寿命计算使用参数如表4所示,计算裂纹深度2～40 mm的车轴剩余寿命结果如图14和表5所示。由图14中可以看出,ΔKth,R=-1的离散性对车轴剩余寿命的影响相较于log10C更为显著,采用中值计算得到的剩余寿命不够保守。

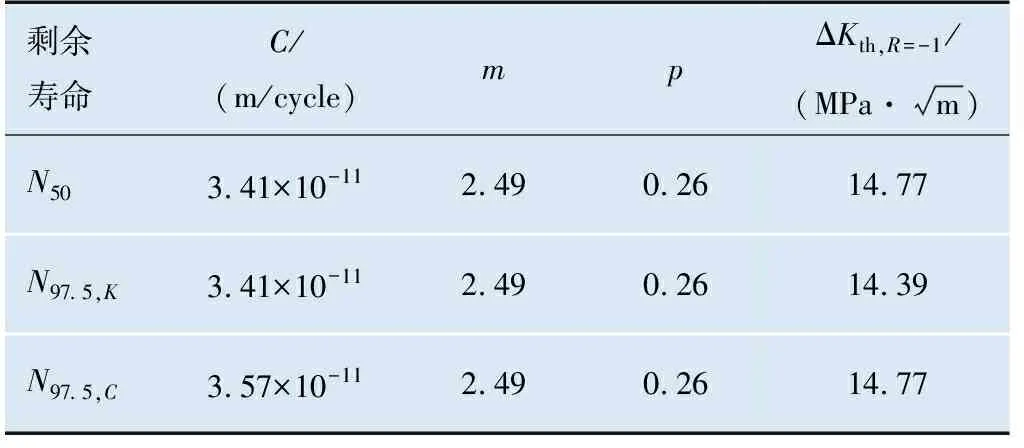
表4 计算剩余寿命N50、N97.5,K和N97.5,C所使用NASGRO方程参数

表5 剩余寿命计算结果

图14 不同方程参数下车轴剩余寿命计算结果

为了表征这种由于材料属性导致的离散性对剩余寿命的影响,引入疲劳安全系数:

(10)

由于上文中车轴疲劳离散性被参数ΔKth,R=-1和log10C所表征。因此,总的疲劳安全系数Lf可以被分为由ΔKth,R=-1离散性引起的安全系数Lf,K和由log10C离散性引起的安全系数Lf,C。Lf、Lf,K和Lf,C之间的关系如下:

Lf=Lf,K·Lf,C

(11)

(12)

(13)

由表5中的剩余寿命计算结果可以得到考虑材料属性离散性的安全系数为:Lf,K=1.21,Lf,C=1.04,Lf=1.26。因此,由参数ΔKth,R=-1和log10C表征的材料属性离散性得到的总的疲劳安全系数Lf=1.26。

4.2 载荷条件

由于仿真所得到的载荷谱不能体现出载荷的统计特性,因此,从文献[31]中选取了相同车型、相同类型车轴、相同截面的实测应力谱来考虑载荷的离散性。

文献[31]中对车轴危险截面弯矩谱进行了统计,其均值μ=21.076 kN·m,标准差σ′=1.12 kN·m,且得到车轴截面弯矩服从正态分布。由车轴弯矩传递系数即可求得车轴截面应力分布参数。车轴弯矩传递系数表达式如下:

(14)

式中:d为车轴截面直径,d′ 为空心车轴截面孔的直径,K′为应力集中系数。

车轴截面应力分布参数结果为:应力幅值的均值为35.89 MPa,标准差为1.91 MPa。计算在97.5%置信度下,应力幅值的上限值σ97.5:

σ97.5=μ+u97.5σ′

(15)

在97.5%置信度下,应力幅值的放大系数计算如下:

(16)

相应地,在考虑裂纹扩展速度最快的线性区,在应力幅值放大1.12倍下,裂纹扩展速率的放大倍数即为考虑载荷条件离散性得到的安全系数为Ll=1.122.49=1.33。

5 车轴检查间隔制定

本文采用车轴探伤最常用的超声波检测作为制定车轴检查间隔的无损检测方法。判断检查间隔是否合适的标准是车轴失效概率小于许用值。累计检出概率和所使用无损检测方法的裂纹检出概率曲线(POD)有关,除此之外还和车轴失效前的检测次数有关。对于超声波检测,图15为采用45°斜探头单边检测到的空心车轴裂纹检出概率曲线[32],探头从空心轴内孔进入。

图15 空心车轴裂纹检出概率曲线

假设POD曲线可以用双参数Weibull分布描述[33],通过拟合可以得到POD曲线的计算公式如下:

(19)

式中:a为裂纹尺寸。

失效概率计算公式如下:

(20)

式中:PODi为第i次测试时的裂纹检出概率。

表6为车轴检查间隔计算。根据图16中裂纹扩展曲线Ndef和图15中的裂纹检出概率曲线可以计算得到车轴失效概率许用值取为0.01的条件下,计算得到检查次数为5,其计算过程如表6所示。

表6 车轴检查间隔计算

图16 剩余寿命计算

6 结论

本文计算了EA4T动力车轴在随机载荷谱下的剩余寿命,并考虑了材料属性和载荷条件2个随机因素对车轴剩余寿命的影响,为车轴检查间隔制定提供了借鉴,得到如下结论:

(1) 以无损检测精度2 mm作为初始裂纹深度并根据实际载荷条件,裂纹尖端应力强度因子范围达到断裂韧度确定临界裂纹深度为40 mm。

(2) 20阶车轮多边形条件下,激发了轮对第十阶、第十四阶和第十六阶高阶模态,进而增加了车轴危险截面的应力,影响车轴的疲劳寿命。

(3) 计算得到的裂纹深度为2～40 mm车轴剩余寿命的中值为38.5万km。

(4) 由小试样试验得到的裂纹扩展数据表现出的材料属性自身的离散性,利用NASGRO方程参数ΔKth,R=-1和log10C来分别表征在裂纹扩展的近门槛区和线性区裂纹扩展速率的离散性,并以此分别得到97.5%置信度下的2个安全系数Lf,K为1.21,Lf,C为1.04,总的安全系数Lf为1.26。

(5) 对于实测载荷中所显现的离散性,在确定其统计特性之后,考虑97.5%置信度得到了一个应力幅值的放大倍数,并以此计算裂纹扩展线性区的裂纹扩展速率放大倍数,进而得到考虑载荷离散性的安全系数Ll为1.33。

(6) 综合2种离散性来修正车轴的中值剩余寿命制定车轴合理的检查间隔为3.8万km。