两种典型地铁受电弓关键部位疲劳失效评价与研究

武 闯,范晨光,2,郭春艳,代成栋,徐剑锋

(1.西南交通大学 力学与航空航天学院,四川 成都 610031;2.西南交通大学 应用力学与结构安全四川省重点实验室,四川 成都 610031;3.西南交通大学 电气工程学院,四川 成都 610031)

随着我国经济的快速发展,公共交通己经无法满足城市的日常客运要求,大多城市开始建设地铁来缓解常规公共交通的压力[1]。接触网是城市轨道交通工程中的重要系统设备之一,它担负着为地铁输送电能的重要作用,目前接触网系统分为两种:架空接触网系统(柔性接触网)和供电轨系统。供电轨系统又分为架空供电轨(刚性接触网)和第三轨两种。其中,架空接触网和架空供电轨由弓网系统供电;第三轨通过靴轨系统供电。接触线高度是指轨道平面与接触线下表面的垂直距离,是表征接触网状态的重要静态几何参数之一[2]。

由于刚性接触网具有空间占用率低、免维护、安全可靠性高等特性,广泛应用于地铁线路段,比如北京、上海、深圳等多个城市的地铁线路正线区段。虽然柔性接触网架设需要极大的空间,其结构复杂,较刚性接触网更易断裂,但由于其具有良好的弹性,可以支持列车高速度运行,因此,地铁线路段往往也会出现大量的柔性接触网区段,比如上海地铁2、3、11号线,深圳地铁11号线和成都地铁18号线等。对于地铁线路接触网系统,柔性接触网段和刚性接触网段是共同存在的[1]。受电弓作为动车组从接触网获取电能的重要电气设备,工作环境非常恶劣,长期受到外部气动载荷、受电弓与接触网之间的振动及摩擦等随机因素的影响,容易发生疲劳破坏。

近年来国内外诸多学者着力于探究地铁受电弓的疲劳寿命预测问题。文献[1—7]建立了受电弓三维有限元模型,通过仿真计算得到应力谱,并对受电弓部件进行寿命预测;陈花丽[6]考虑了弓网耦合作用下受电弓参数改变对接触网寿命的影响;黄思俊[7]等利用HyperMesh建立受电弓的有限元模型,将疲劳寿命分析方法运用到受电弓系统的随机振动中,评估随机振动载荷作用下高速受电弓的疲劳强度。以上研究多是基于仿真分析得到受电弓的应力谱,然后进行疲劳寿命预测,对于受电弓经过刚柔接触网过渡段时(即导线高度突变时)部分部件的应力发生跳变的现象关注较少。本文采用现场实测的应力时程数据对受电弓的关键部件进行疲劳可靠性分析,并且着重关注导线高度突变部分对受电弓疲劳寿命的贡献,为后续对地铁受电弓的安全性评估提供参考。

1 问题提出

1.1 受电弓运行状态下的受力特点

受电弓属于轨道交通车辆受流装置,安装在车辆顶部,与供电网接触,集取接触网电流,供地铁车辆运行使用。受电弓在正常运行过程中,不断与接触网产生摩擦,直接受到弓网接触交变载荷作用;尤其是经过接触网刚柔过渡段时,由于导线高度的剧烈变化,会产生瞬间的冲击作用,引起结构较强的振动响应,应力幅值也相应地产生较大的变化。某型号受电弓[8]运行里程在50.4～65.5万km时,上框架处产生了裂纹,如图1所示。

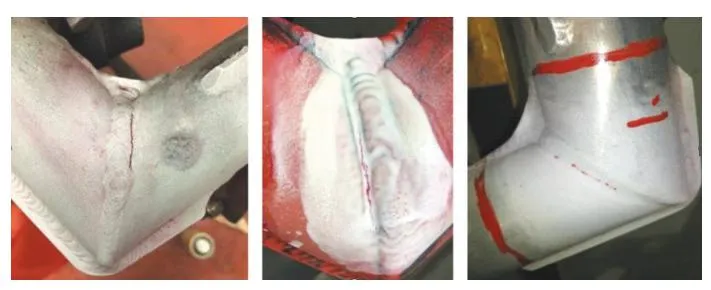
图1 某型号受电弓上框架焊趾处裂纹[8]

本文基于国内某地铁线路的弓网线路试验,分析两种不同受电弓的载荷特性。通过线路试验测试接触网线路导线高度变化、各部件的应力变化等。在受电弓关键部位粘贴应变片,如图2所示。受电弓升起后由于受到各种外力,张贴在其表面的应变片阻值发生改变,通过应变采集系统计算出相应的应变数值。应变信号采集使用美国NI-9235C系列应变/桥输入模块,通过高压采集箱将信号引入车内。在受电弓开口方向前端安装滑板动态高度检测相机,如图3所示,用来检测导线高度变化。地铁车内配电柜提供220 V交流电,此外,为了防止车辆意外断电的情况,通过稳压器和UPS给检测设备供电。

图2 局部应变片布置

图3 受电弓导线高度参数测量装置

1.2 正线测试结果及参数影响分析

试验工况为地铁正线ATO模式(列车自动驾驶系统,能够实现列车自动行驶、精确停车、站台自动化作业、无人折返、列车自动运行调整等功能),线路全长51 km,弓网静态接触力为120 N。为对比两种受电弓性能差异,两种型号受电弓均采用了相同的碳滑板。在测试完成后,将碳滑板拆除,安装在下一次测试的受电弓弓头上,以确保试验遵循单一变量原则。分析碳滑板高度变化曲线,地铁线路由柔性接触网和刚性接触网混合编制而成,刚性网局部导线高度出现较小的跳变,刚性网与柔性网交界处导线高度出现了较大跳变。其中刚性接触网区段占比较大。如图4所示,刚性接触网区段,接触网导线高度有4 040 mm和4 200 mm两种,而柔性接触网区段,接触网导线高度为4 640 mm。

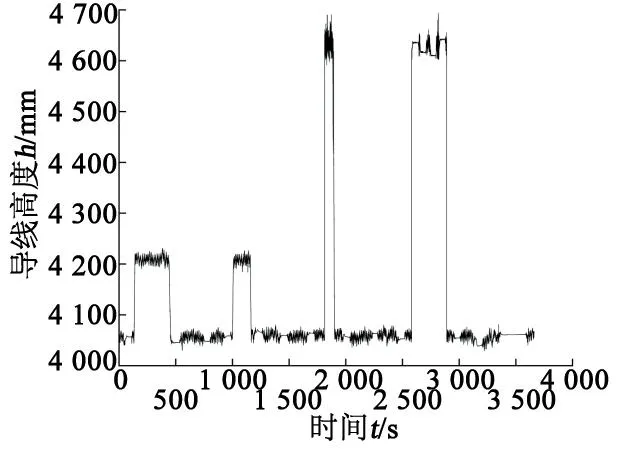
图4 全程导线高度时程曲线

首先对受电弓进行有限元静力学分析得到各部分的应力分布,找到应力较大的部位,由此来确定应变测点的位置。根据有限元静力学仿真结果,应力较大的部位主要集中在受电弓上框架、下臂杆和底架处,在这些位置的测点布置了应变片;同时还在弓头、拉杆、平衡杆处布置了测点,测点布置如图5、图6所示。由此可以全面准确得到整个受电弓的应力分布状态。材料参数如表1所示。试验表明,当受电弓经过接触网导线高度变化区段时,由于接触网导线高度的变化引起的应力突变部位主要位于底架、上框架及其附属连接部分。

表1 受电弓各部件参数统计

图5 A型受电弓测点布置图

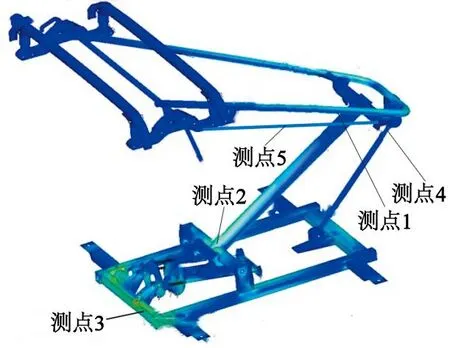
图6 B型受电弓测点布置图

选取A型受电弓的测点5(拉杆连接件)处,工况选取为前弓ATO模式;B型受电弓的测点3(底架)处,工况选取为后弓ATO模式。两测点的应力时程曲线如图7、图8所示,从图中可以看出,应力突变发生时间与全程导线高度时程曲线的突变位置基本吻合,由此判断应力突变是由导线高度变化引起的;并且在导线高度不变的稳定段,应力波动不大。

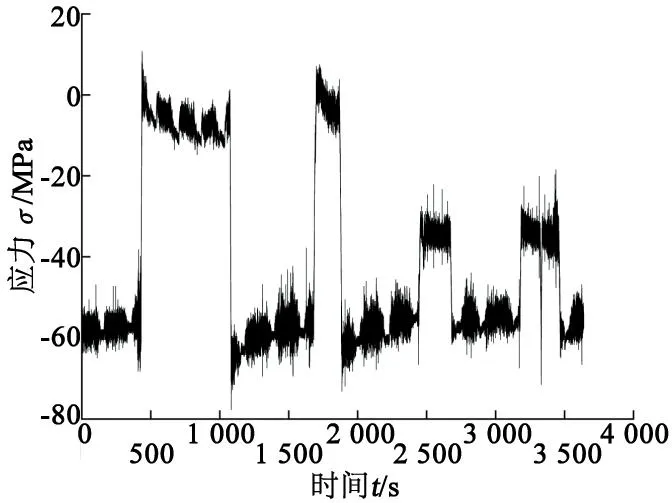
图7 A型受电弓测点5应力时程曲线

图8 B型受电弓测点3应力时程曲线

地铁正线运行时,受电弓与接触网直接接触,由于接触网性质的改变引起较大应力幅值的突变并且这种突变是周期性的,这种周期性的交变载荷可能会导致受电弓各部件产生疲劳破坏,危及行车安全,严重情况下可能导致线路停运。因此有必要对受电弓进行疲劳寿命预测以确保弓网系统正常运行。

2 受电弓疲劳可靠性研究

受电弓所受到的外界载荷为随机交变载荷。疲劳载荷的描述中使用应力幅值σa和应力范围Δσ以及平均应力σm表示[9]:

σa=1/2(σmax-σmin)

(1)

Δσ=σmax-σmin

(2)

σm=1/2(σmax+σmin)

(3)

本文对受电弓的疲劳寿命进行预测,具体方法如下:

(1) 对采集到的应变数据进行处理(σ=Eε),得到受电弓各部件动应力时程曲线;

(2) 通过双参数雨流计数法实现对应力幅值和均值的统计,得到非对称二维应力谱;

(3) 考虑雨流计数统计的具体情况,对材料的S-N曲线修正,得到构件的P-S-N曲线;

(4) 采用“波动中心法”得到非对称一维应力谱并经过Goodman直线修正,得到其8级对称应力谱;

(5) 基于结构8级应力谱统计结果,结合材料P-S-N曲线和Miner线性累积损伤理论,对受电弓关键部件进行疲劳寿命预测。

总体技术路线如图9所示。

图9 技术路线

2.1 雨流计数法

雨流计数法是20世纪50年代由英国的两位工程师MATSUISHI和ENDO提出来的[10]。为保证载荷谱块的完整性,将前弓与后弓的应力测试数据拼接起来作为完整的应力时程曲线进行统计。

文章采用雨流计数法对动应力时程数据进行统计分析,基于软件编程实现[11-13]。具体步骤如下:

(1) 对应力时程信号再造,使其只包含峰谷值。原始信号应定义为Ci,同时令Ai=Ci,Bi=Ci;依次判断Ai数据,如果不满足峰谷值判断条件,记相应下标Bi为NaN并删除元素,同时实现等数值压缩,得到处理后新载荷时间历程记作Bi。

(2) 用四峰谷值法对Bi进行一阶段雨流计数。定义两个空数列F、J用以存储应力循环的幅值和均值。当length(Bi)>3,令前两个点的差值c=0(首次计数人为给定),计算a1=abs(Bj+1-Bj),a2=abs(Bj+1-Bj+2),m3=(Bj+1+Bj)/2。

如果满足应力循环判断条件a1≤a2且a1≤c,则提取循环幅值a1/2,均值m3,分别记录在数列F、J中,同时删去Bj和Bj+1两点。为了存储提取的载荷点,将定义数列D,依次将Bj、Bj+1、Bj填入,用NaN与下一个循环隔开。此时再令c=a1,继续循环。

(3) 一阶段雨流计数结束后,剩下的发散-收敛波形无法构成循环,寻找最高波峰(最低波谷)点,从该点处截断,左右两应力波段对换位置首尾相接,形成收敛-发散波形,返回步骤(2),继续循环。

(4) 直到length(Bi)<3,跳出循环。记录最后一个应力循环,此时幅值为(Bmax-Bmin)/2,均值为(Bmax+Bmin)/2,程序结束。

数据处理步骤如图10所示。

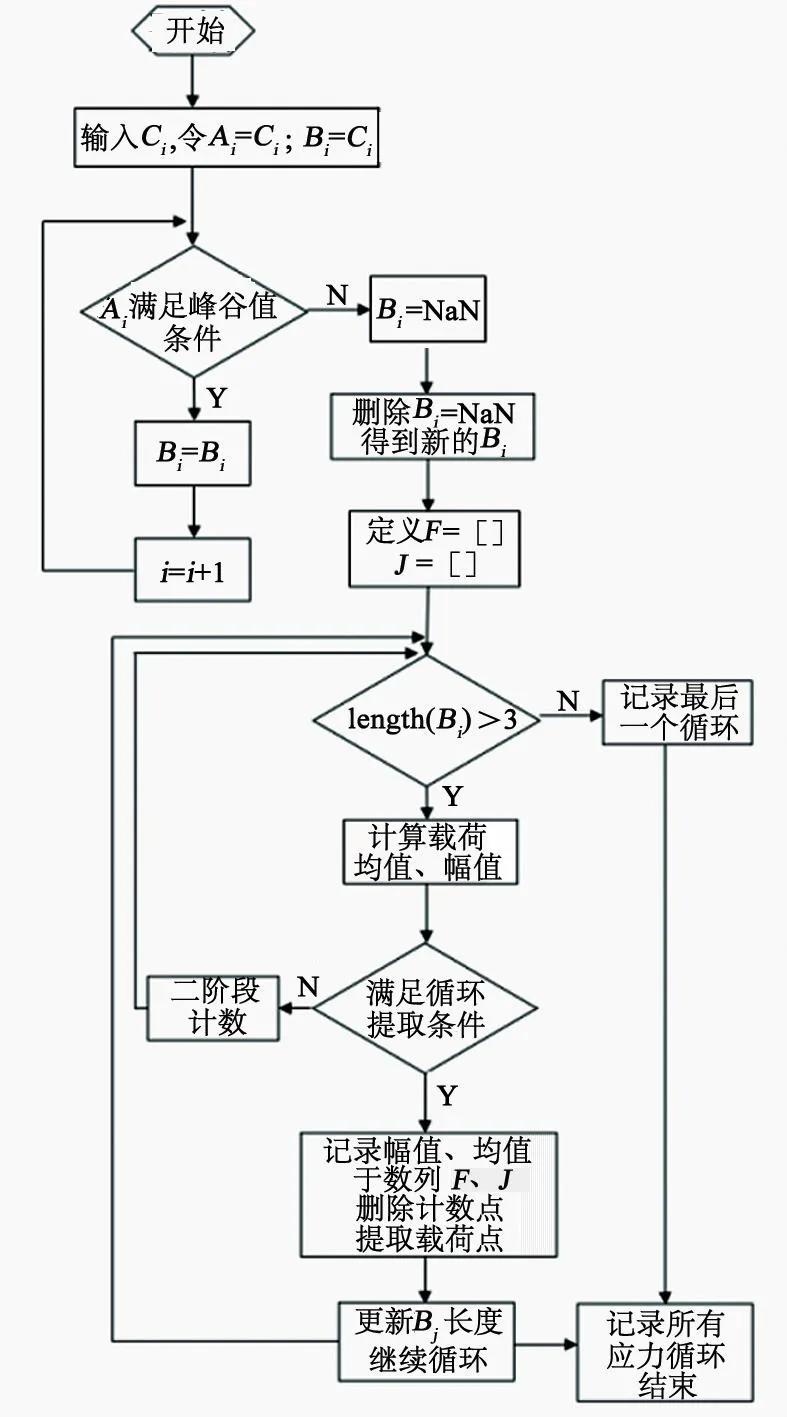
图10 雨流计数程序流程图

2.2 P-S-N曲线

采用如下公式估算受电弓材料在指定概率P下的疲劳寿命[1]:

(lgN)P=AP+BPlgS

(4)

式中:AP和BP分别为截距参数和斜率参数;N为疲劳寿命;S为应力幅值;P为存活概率。

传统的疲劳寿命理论认为当应力幅值低于材料疲劳极限时,结构不会出现疲劳结构破坏,认为此时结构为无限寿命。但是在工程实际中,受电弓结构在低应力幅值工作下,其结构依然会出现疲劳损伤问题。因此,采用2m-1指数法外推得到材料的P-S-N曲线。计算公式如下:

(lgN)P=EP+FPlgS

(5)

不同存活概率下的外推P-S-N曲线参数取值如图11、图12所示。

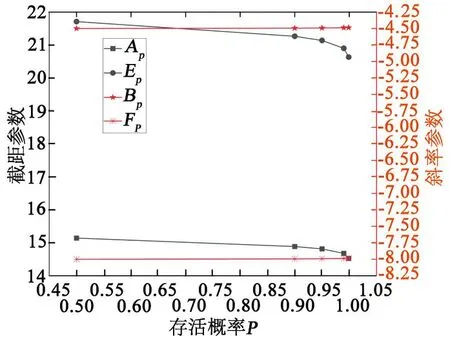
图11 铝合金材料P-S-N曲线参数

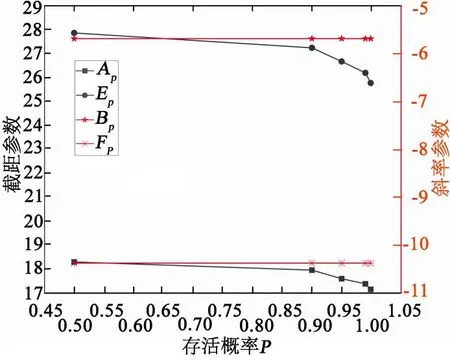
图12 不锈钢材料P-S-N曲线参数

2.3 一维载荷谱编制

应力时间历程经雨流循环计数处理之后得到的输出数据文件为整个历程中各次应力循环的均值和幅值。由于数据量大,不便于统计,因此有必要对数据进行整理,编制出一维应力谱。

采用“波动中心法”,只考虑应力循环的幅值而不考虑应力循环的均值,将应力谱简化为一元随机变量,具体方法如下[14]:

(1) 检索均值数据,计算所有应力循环的总平均值作为波动中心。

(6)

式中:M为波动中心;Mi为第i级应力均值;ni为第i级应力均值对应的频次。

求得波动中心后,将幅值作为应力循环的动应力分量叠加于波动中心之上。

(2) 检索幅值数据,求得应力幅值最大值和最小值的差值Δ。由于实测应力波数据的特殊性,幅值统计数据呈现两端多,中间少的特点,因此采用非等距数值进行分组[15]。

(7)

式中:Ri为组间距;N为应力幅值级数,i=1,2…N-1。

(3) 依次读取幅值数据,判断应力幅值属于哪一级应力范围之内,存储于新建变量之中。为统计方便,各级应力幅值组采用其组中值来表示。

由于测点数较多,选取受电弓关键部位的一维应力谱,如表2、表3所示。从表中可以看出,低应力幅值占总计数的绝大多数,这是由于受电弓在恒定工作高度运行稳定的结果;高应力幅值占比较小,是由于导线高度突变次数较少产生的结果。

表2 A型受电弓各部件8级应力谱

表3 B型受电弓各部件8级应力谱

统计分析得到8级非对称应力谱,为保守估计,基于Goodman方程对应力谱进行修正,将其转化为对称循环应力谱,修正公式如下[9]:

(8)

式中:σN为对称循环应力幅值;σa,σm为应力循环的幅值和均值;σu为材料极限强度。

2.4 疲劳寿命预测

文献[16]详细介绍了线性、非线性、两级线性疲劳累积损伤理论。Miner线性累积损伤理论是工程上广泛采用的一种疲劳寿命计算方法。

经典Miner线性累积损伤理论认为,各级应力造成的损伤可线性叠加,当总损伤量D达到1时结构发生破坏。对于一个8级载荷谱而言,累积的总损伤为:

(9)

式中:ni为第i级应力水平下的循环次数;Ni为第i级应力水平下的寿命。实际运营时考虑安全与可靠性,D一般取0.7[17]。

由实测数据,该8级应力谱对应的测试里程L1为102 km,根据Miner线性累积损伤理论,可知结构在存活概率P下运行的总里程L为:

L=L1D/D8

(10)

统计结果如表4、表5所示,可以看出,随着可靠度的增加,受电弓各部件的疲劳寿命逐渐减小;对于A型受电弓,上框架处寿命最短,容易产生裂纹,应关注;下臂杆和弓头连接件寿命相近,底架、拉杆处均为长寿命;对于B型受电弓,同样是上框架的寿命最短,应关注;底架次之,下臂杆、平衡杆、拉杆处均为长寿命。

表4 A型受电弓ATO工况各部件寿命预测 万km

表5 B型受电弓ATO工况各部件寿命预测 万km

参照文献[17]的5.3小节,受电弓的设计寿命里程不应少于1.2×103万km。A型受电弓的预测运行里程为7.72×103万km,B型受电弓的预测运行里程为3.22×103万km,由此可见,两种型号的受电弓在ATO工况运行状态下,各部件均满足寿命设计要求,但B型受电弓的寿命较短。

3 结论

基于A、B两种不同型号的受电弓现场试验测试结果,得到受电弓全程ATO工况的动应力载荷谱;应用雨流计数递归算法实现雨流计数程序设计并对受电弓部件进行疲劳可靠性分析,得到以下结论:

(1) 在导线高度不变的情况下,速度等级变化产生的交变应力幅值很小,对受电弓寿命的贡献几乎可以忽略不计;导线高度变化时,会对受电弓产生冲击因而出现较大的应力幅值;

(2) 对于改进后两种型号的受电弓来说,最短寿命预测结果均为上框架部位,且B型受电弓的寿命较短,但都满足寿命设计要求;

(3) 在搭建接触网系统时,应尽量减小接触网之间落差以降低应力突变,提高受电弓的疲劳寿命。