基于LMD-MFE-SVD的松动爆破降噪分析*

周红敏,赵事成,王慧珍,余 辉,2,李文豪,张宪堂,2

(1.山东科技大学 山东省土木工程防灾减灾重点实验室,青岛 266590;2.安徽理工大学 矿山地下工程教育部工程研究中心,淮南 232001)

松动爆破作为相对成熟的爆破技术,多用于矿山开采和基坑开挖。在进行松动爆破振动监测时,周边环境间断噪声多、噪声类型复杂,且松动爆破的段别间隔时间长,更易受到噪声的干扰,对信号降噪模型的性能和效果提出更高要求。经验模态分解(empirical mode decomposition,EMD)作为主要的信号消噪方法,因其在处理非线性、非平稳信号时降噪效率稳定,在爆破振动信号分析领域中得到广泛应用[1]。然而EMD在处理间断噪声时会出现明显的模态混叠现象,对分解精度产生不利影响。为了解决该问题,学界相继提出了集合经验模态分解(ensemble empirical mode decomposition,EEMD)[2]、互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)[3]和改进的经验模态分解方法(modified ensemble empirical mode decompostion,MEEMD)[4]等一系列改进算法,在爆破振动和故障检测领域进行应用,取得了较好的去噪效果。而为处理模态分解类算法的端点问题,学界又陆续提出极点对称分解算法(extreme-point symmetric mode decomposition,ESMD)[5]和基于模态分解类的熵值筛选算法,有效解决了固有模态分量((intrinsic mode function,IMF)筛选过程的端点问题。

IMF分量本质为调频信号,重构信号准确度更多取决于对IMF分量的人为界定,降噪效果波动较大[6]。为处理上述问题,Smith在进行脑电感知数据处理时提出局部均值分解(local mean decomposition,LMD)方法[7]。程军圣等建立仿真信号用于LMD方法降噪效果验证[8],表现出良好的信号处理能力。后续李伟将LMD方法应用于矿山微震信号提取[9],取得了可观的分类准确率。然而LMD方法仍存在缺陷:其一,LMD方法更多应用于机械故障检测、脑电信号提取领域,其他领域的拓展较少;其二,在使用LMD方法对信号进行分解,需要有效判断噪声分量与真实分量的界限,而界限判断的难易多取决于信号的复杂程度。

基坑开挖时周边环境嘈杂,工程机械施工噪声大,振动信号成分复杂,对降噪精度要求更高。基于上述问题,本文建立一种基于LMD-MFE-SVD的爆破振动信号降噪模型,对松动爆破振动信号进行LMD分解,得到乘积分量(product function,PF);结合相关系数和多尺度模糊熵(multiscale fuzzy entropy,MFE)进行PF分量筛选,对含噪分量进行SVD滤波得到更准确的爆破振动信号,为后续信号分析提供依据。

1 模型理论基础

1.1 LMD原理

LMD方法是一种新的自适应非平稳信号的分析处理方法,从原信号分解出若干PF分量,每个PF分量都是单个包络信号和对应调频信号的乘积,其分解过程如下[10]:

(1)确定原信号x(t)的局部极值点,计算相邻两个极值点的平均值ui和包络估计值vi。

(2)将全部相邻的局部均值ui和局部包络估计值vi分别用折线连接,采用滑动平均方法对其进行平滑处理,得到局部均值函数u11(t)和局部包络估计函数v11(t),从原始信号中剔除u11(t)得到零均值函数h11(t)。

(3)对h11(t)进行解调,得到解调信号l11(t)

(1)

(4)将l11(t)作为原始信号,计算包络估计值v12(t),若v12≠1,重复步骤(1)、(2),迭代n次后得到的l1n(t)为纯调幅调频信号,则迭代停止,可得到下式

h1n(t)=l1(n-1)(t)-μ1n(t)

(2)

考虑到l1n为纯调幅调频信号为理想情况,实际中为使v1n(t)更快收敛,可进行简化处理。设置增减量为δ,使|1-v1n(t)|≤δ,则计算对应的包络信号如下

(3)

(5)将纯调幅调频信号l1n(t)与包络信号v1(t)相乘得到乘积函数PF1

PF1(t)=v1(t)l1n(t)

(4)

式中,v1(t)为乘积函数PF1的瞬时幅值。

(6)从原信号x(t)中分离出乘积函数PF1,得到新的函数w1(t),重复步骤(1)～(5),直至残差分量wj(t)为常值或单调函数,可得到下式

wj(t)=wj-1(t)-PFj(t)

(5)

原始信号x(t)可分解为j个PF分量和一个残差分量的wj(t)和,则原始信号x(t)重构为

(6)

1.2 MFE原理

熵是时间序列复杂性的度量,多尺度模糊熵可代替一般熵中的硬阈值准则,用以衡量时间序列于不同尺度因子下的复杂性和自相似性,统计结果稳定性更好[11],其计算步骤如下:

(1)将原始时间序列粗粒化

对长度为N的原始序列Xi={x1,x2,…,xN},预先设定嵌入维数m和相似容限r,建立粗粒向量yi(τ)

(7)

式中:τ为尺度因子,τ=1;yj(1)为原序列。对于非零τ原始序列Xi可分为τ个每段长为N/τ的粗粒序列yj(τ)。

(2)计算多尺度模糊熵

对全部粗粒序列计算模糊熵,可认为其为尺度因子的函数,即多尺度模糊熵。通常认为熵值越小,序列的自相似性越高;熵值越大,序列越复杂。

1.3 SVD滤波原理

SVD 是线性矩阵理论中的重要工具,目前已经广泛应用于工程降噪领域。一般认为,SVD值越大则对应能量较大或者能量集中信号,SVD值越小对应能量较小或者能量分散的信号[12]。

(1)构造Hankel矩阵

对于一维序列Xi={x1,x2,…,xN}构造Hankel矩阵。

(2)对矩阵H进行SVD滤波

(8)

式中:U1、W1、V1为较大奇异值;上标H表示共轭转置。

(3)重构滤波后信号

(9)

1.4 LMD-MFE-SVD混合去噪方法

针对松动爆破信号的特点,建立一种基于LMD-MFE-SVD的混合去噪方法,算法步骤见图1。

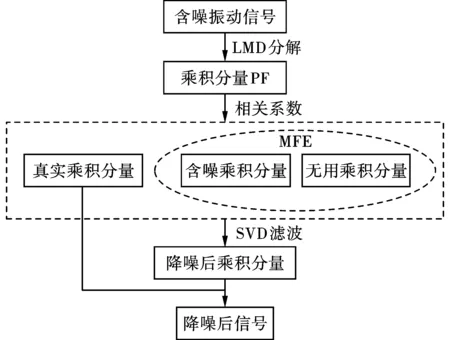
图1 LMD-MFE-SVD流程图Fig. 1 Flow chart of LMD-MFE-SVD

2 仿真信号分析

2.1 建立仿真信号

为充分检验改进算法的可行性,有效计算信号熵值,合成由真实信号和噪声信号组成的仿真信号。真实信号包括低幅值低频余弦信号x1(t)、低幅值高频余弦信号x2(t)、调幅调频信号x3(t)和多频信号x4(t)、x5(t),噪声信号包括间接噪声x6(t)和高斯噪声x7(t)。

仿真信号表达式如下

2.2 仿真信号分析

对仿真信号进行LMD分解,可得到6个PF分量,如图2所示,各分量的相关系数依次为0.5178、0.6097、0.2560、0.2233、0.3907和0.1249,多尺度模糊熵值见表1。考虑到仿真信号由7类信号构成,分解得到的PF分量相关系数普遍较小,故本文相关系数阈值取0.2[13]。通过表1可知,PF1分量的多尺度模糊熵最大,且随着维度的增加而减少,与其余分量呈相反变换规律。参考相关系数,PF1分量为含噪乘积分量,PF2～PF5为真实乘积分量,而PF6为无用分量。

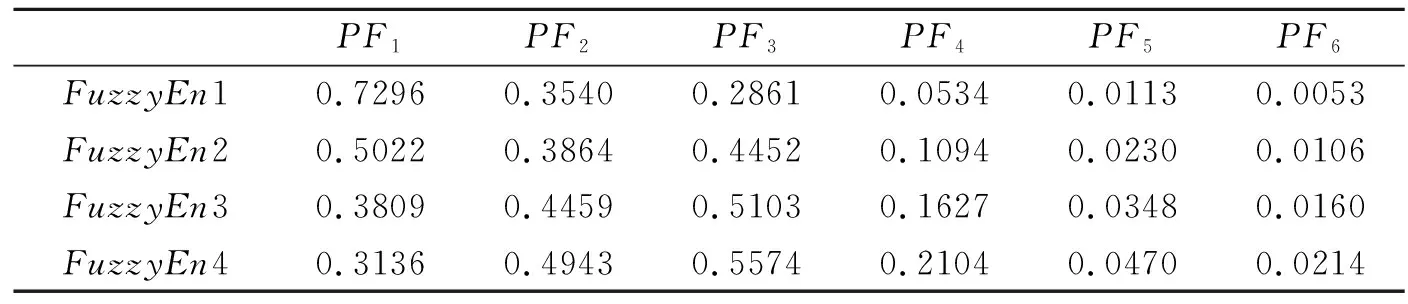
表1 PF分量模糊熵Table 1 Fuzzy entropy of PF

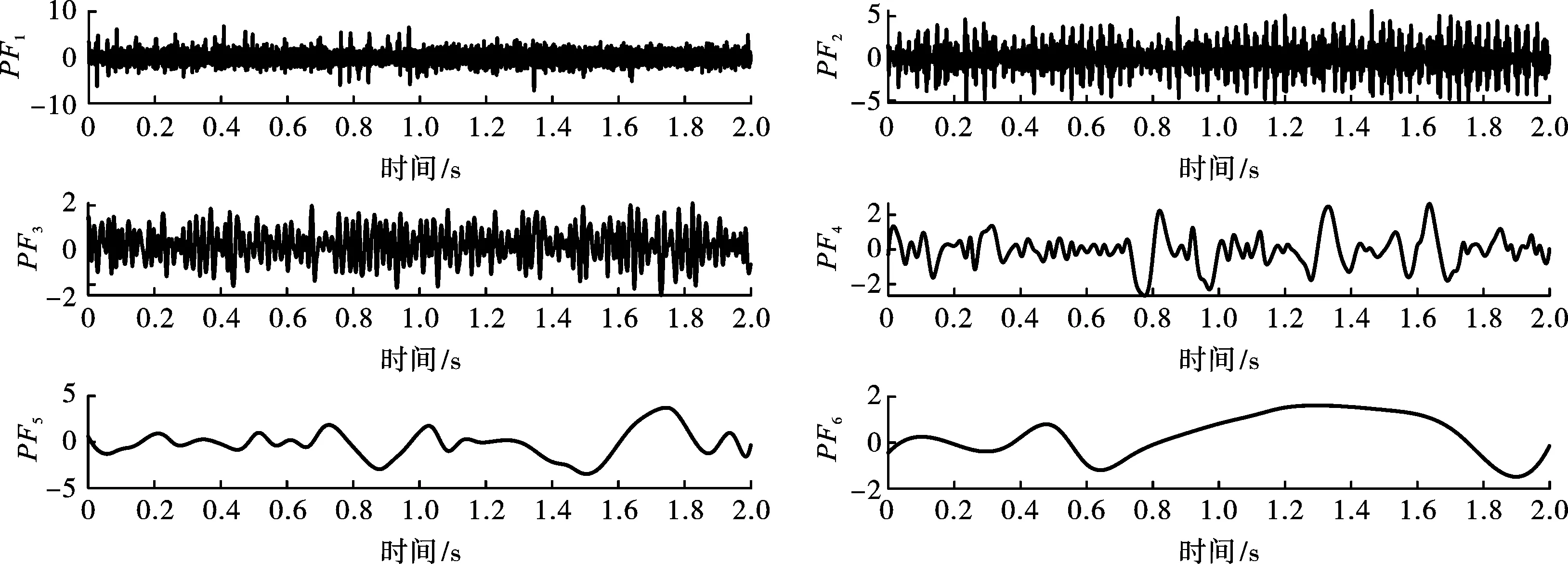
图2 仿真信号LMD分解Fig. 2 LMD decomposition of simulated signal

对PF1进行SVD滤波去噪,具体去噪效果见图3。通过观察图3(a)可知,SVD滤波对噪声分量进行了有效提取,得到了部分的信号特征;观察图3(b)可知,SVD滤波降噪后的信号更为集中,噪声分量得到了有效的剔除,具备一定的降噪效果。

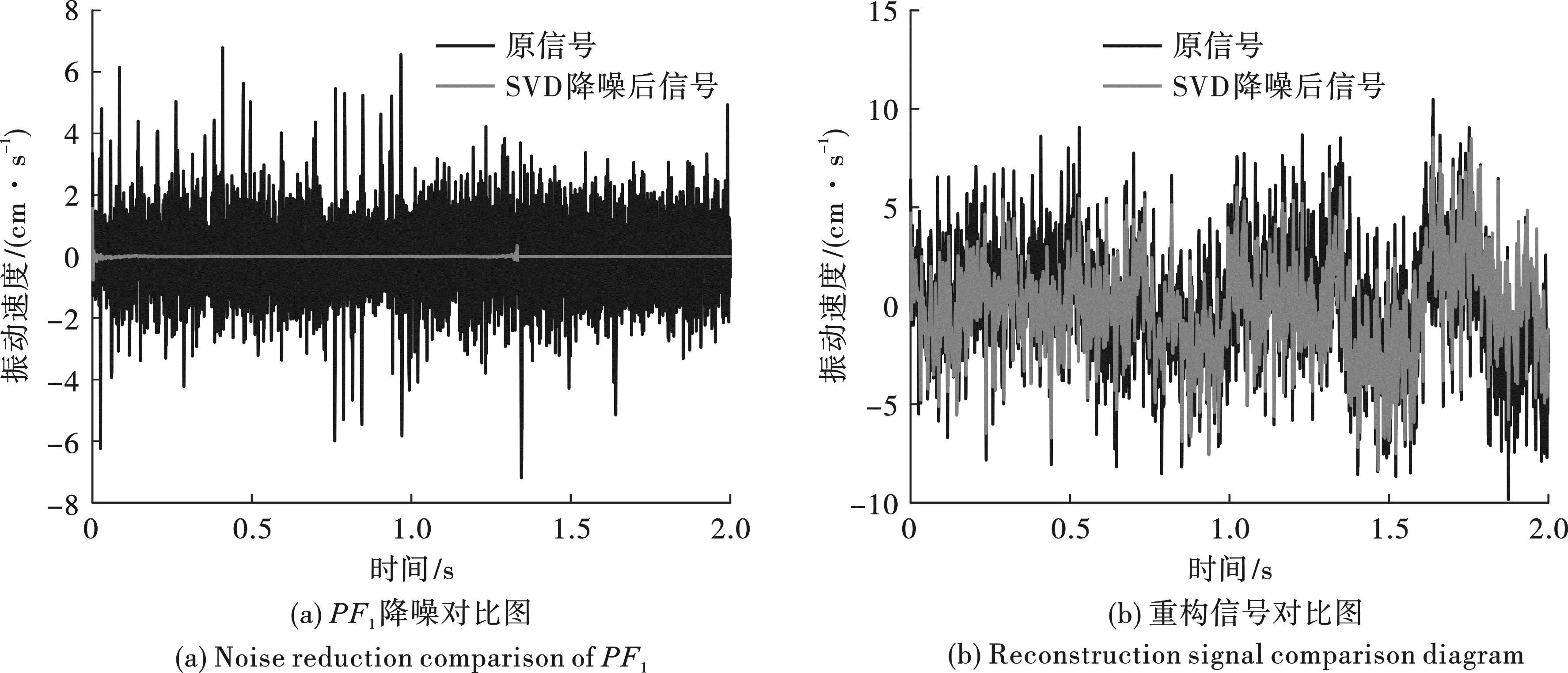
图3 SVD滤波降噪效果Fig. 3 SVD filtering Noise reduction effect

2.3 算法优劣对比

为更好比较改进算法的优劣,引入EEMD、CEEMD、MEEMD和LMD对仿真信号进行分解。采用信噪比(SNR)[14]、均根方误差(RMSE)、失真百分比(PRD)对消噪质量进行量化分析。输入仿真信号进行分解,EEMD、CEEMD和MEEMD等5类算法得到的分量相关系数见图4,降噪指标数据见表2。通过图4可知,对于成分复杂、具有多类噪声的复杂信号,LMD类方法能够以更少的模态分解次数完成信号的整体分解,PF分量相关系数整体呈递减趋势,表现出良好的分解稳定性,仅IMF5分量作为折线凸点出现,与第二段的间接噪声有关。而EEMD类分解方法中的IMF6～IMF8整体作为凸点出现,可认为EEMD类方法难以有效处理间接噪声的出现,即对于间接出现的高频噪声,EEMD分解类算法处理的稳定性低于LMD类算法。参考表2可知,LMD类算法整体指标表现依次提升了71.62%、39.51%和35.71%。而提出的LMD-MFE-SVD算法相较LMD算法的性能略有提升,依次提升了11.73%、22.07%和9.25%,处理复杂信号的降噪效率和精确度更高。

表2 降噪指标表Table 2 Noise reduction index table

图4 相关系数图Fig. 4 Correlation coefficient diagram

3 实测信号分析

3.1 爆破振动监测

工程监测地点位于青岛市平度市旧店镇金山路1号,处于青岛金星矿业现有矿山1#风井工业场地内,主要构筑物包括工业厂房、缓冲池、混凝反应池、高效斜板沉淀池、污泥浓缩池等,多为钢砼结构。施工位置处于厂区地磅房西南方向,邻近缓冲池和主要厂房。工程采用浅孔松动爆破技术,YT28凿岩机进行钻孔,炮孔孔深2.2～2.3 m,炮孔直径40 mm,共布设6个炮孔,炮孔间孔距、排距依次为1.5 m、1.5 m,最大单段药量为2.4 kg,单次爆破总药量为7.2 kg。采用2号岩石乳化炸药进行连续不耦合装药,对所开挖的基坑石方进行多段松动爆破,产生的爆破振动可能对厂区内既有的衬砌结构产生不利影响[15]。监测场地周围共布设4个爆破监测点,对土石方松动爆破进行监测,具体测点布设位置可见图5。

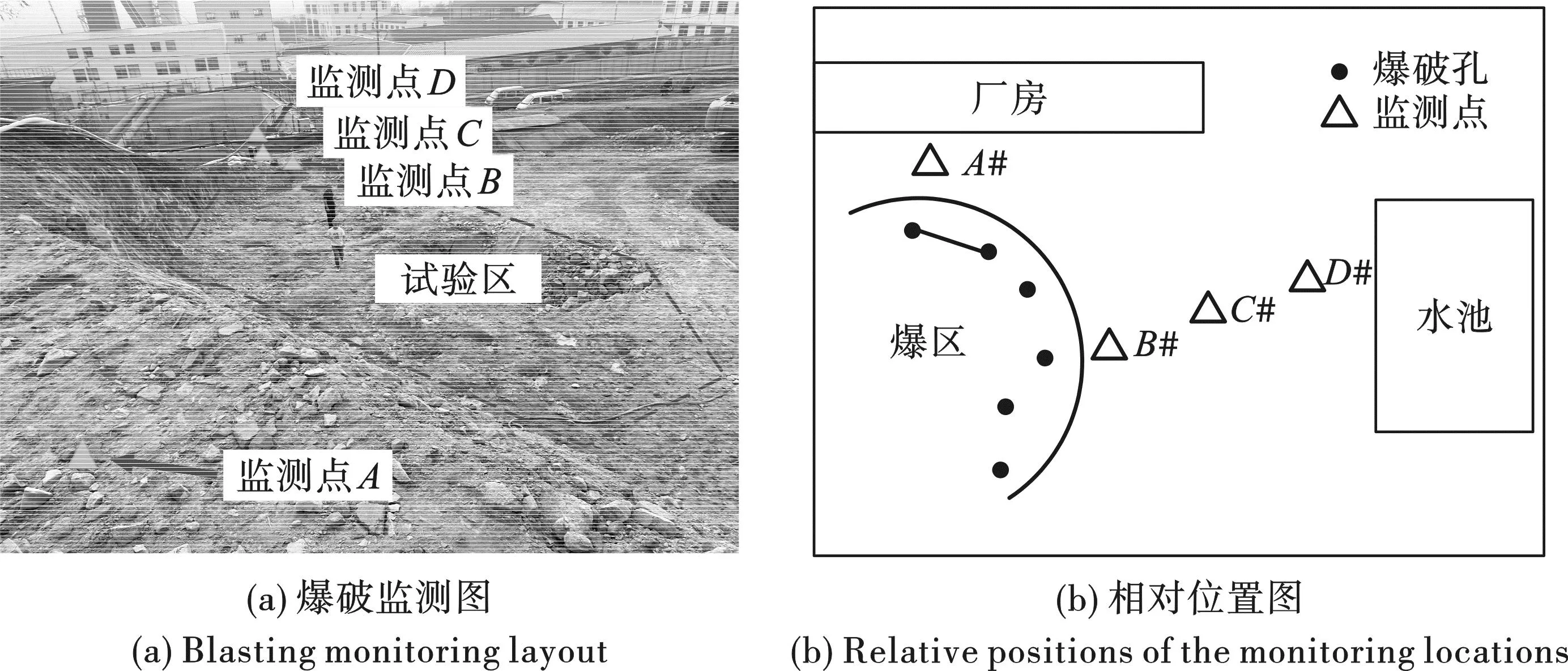
图5 爆破测点布设图Fig. 5 Blasting measuring point layout diagram

为充分考虑松动爆破对相邻建筑物的影响[16],取监测点A测振数据作为实测信号,采样频率为8000 Hz,其振动信号如图6所示。通过振动信号可知,本次松动爆破共进行了6个段别的起爆,第5～6段起爆间隔时间较短,依次为0.4 s、1.0 s、0.4 s、0.85 s和0.15 s,考虑到松动爆破的各段间隔时间均大于0.1 s,可基本认为各段起爆之间的相互影响较小。松动爆破中Z向振速最高,最高振速为1.37 cm/s,单段爆破持续时间约为0.6 s。

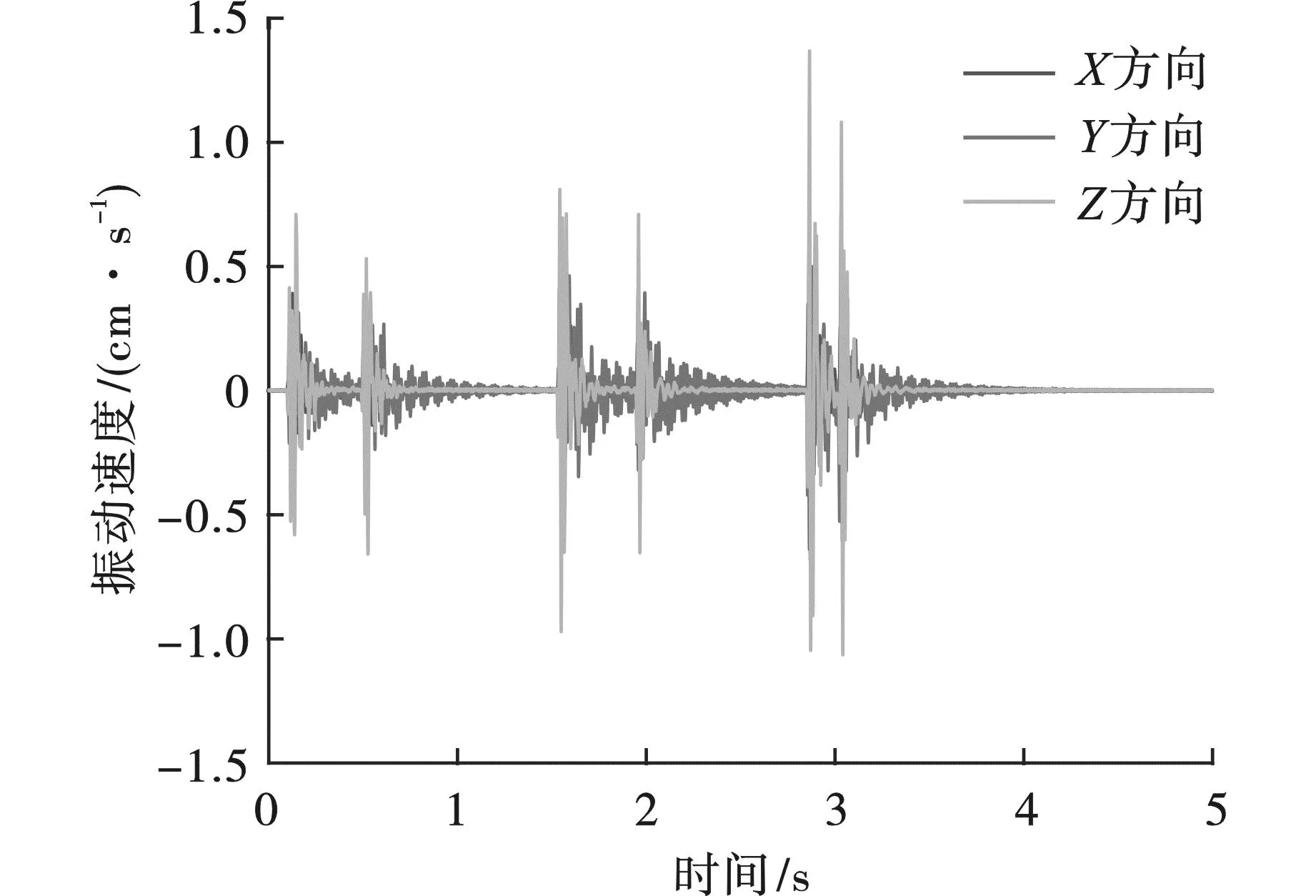
图6 监测点A爆破振速图Fig. 6 Monitoring point A blasting vibration velocity diagram

3.2 实测信号分析

为充分检验LMD-MFE-SVD算法对实测松动爆破振动信号的适用度和降噪性能,选取0.4～1.2 s、2.7～4.1 s两段Z方向的振动信号进行分解,其中0.4～1.2 s为较完整的松动爆破信号,而2.7～4.1 s为信号中的高振速高频信号段,可能对监测点附近的厂房造成振动损害[17],分解得到表3。通过分析表3可知,0.4～1.2 s信号段分解得到的PF分量中,PF2、PF3两分量为含噪分量,而PF4、PF5为无用分量;2.7～4.1 s信号段中,PF4、PF5和PF6分量为无用分量,PF3为含噪分量。

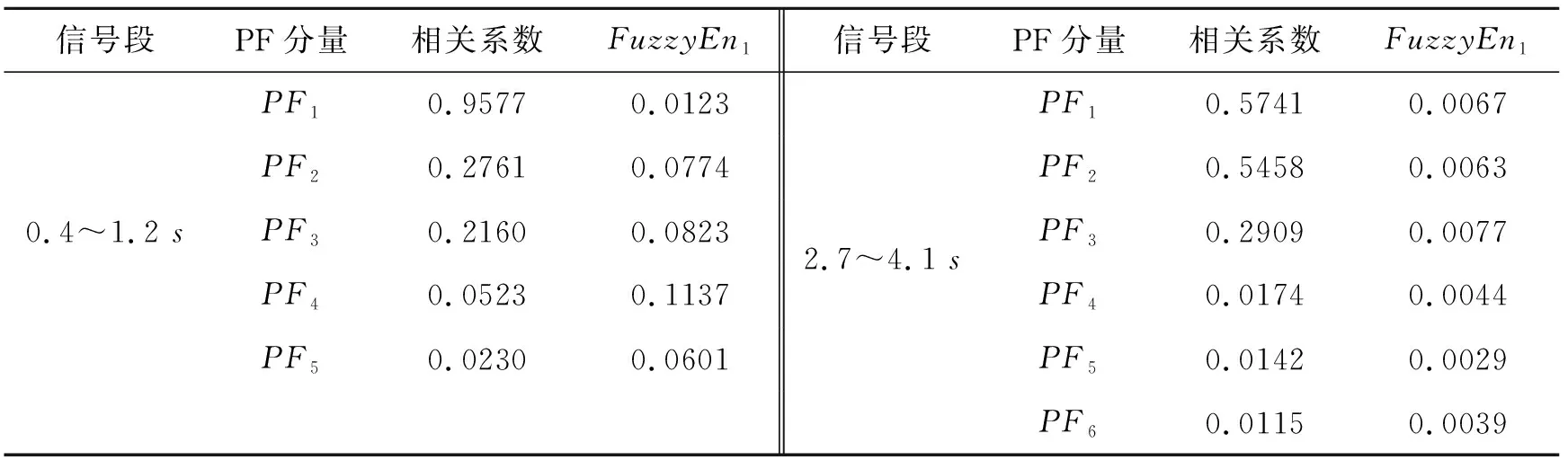
表3 LMD-MFE-SVD分解过程参数表Table 3 Parameter table during the LMD-MFE-SVD decomposition process

将0.4～1.2 s和2.7～4.1 s的松动爆破信号进行重构,对0.4～1.2 s信号中的PF2、PF3分量和2.7～4.1 s信号中的PF3分量进行SVD滤波降噪,得到的信号波形及频谱图如图7、图8和图9所示。观察图7可知,提出的LMD-MFE-SVD降噪方法能较好处理松动爆破信号,受限于整体信号段划分的影响,受到邻近波段干扰,信号起始部分有部分过度滤波的情况,但整体的降噪效果良好,波形更为集中,且有效消减了0.7～1.2 s和3.2～4.1 s信号段的模态混叠现象。观察图8、9可知,去噪后的频谱图更为清晰集中,能够明显标示出信号的高频波峰,更有利于对信号的频谱分析。

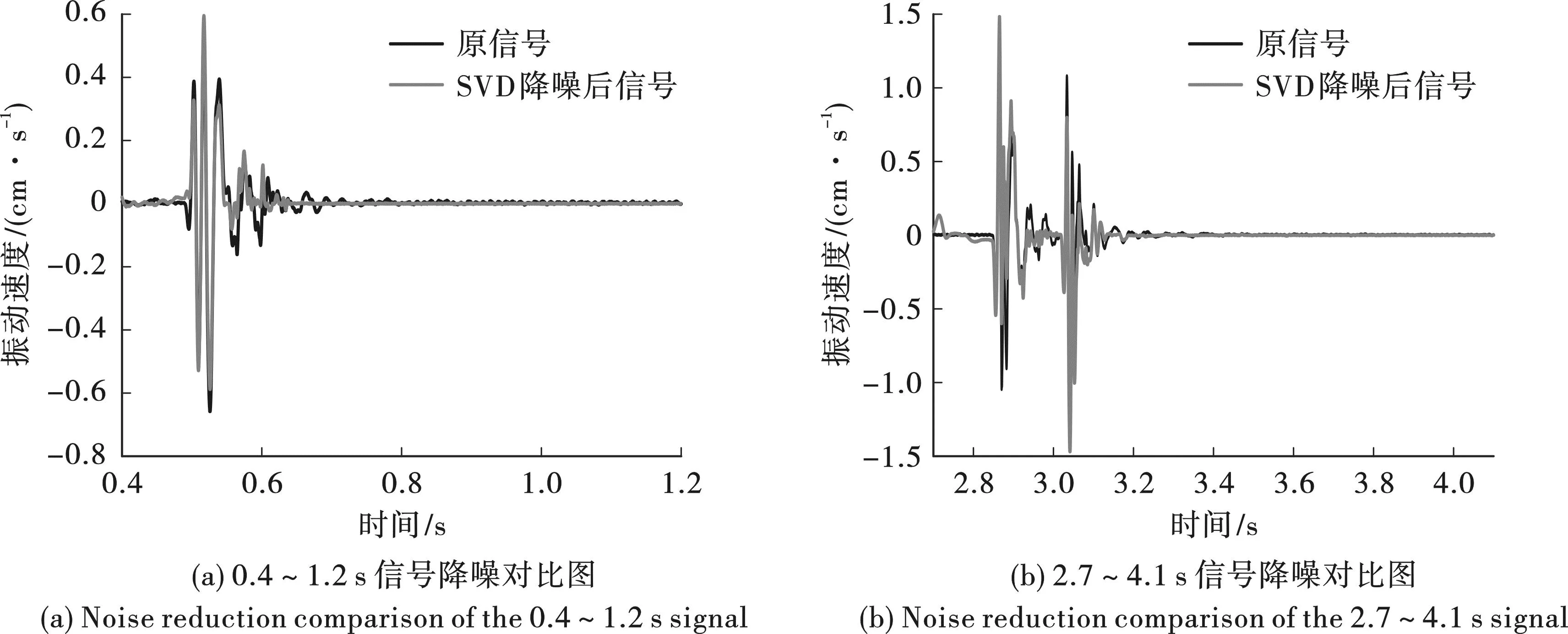
图7 原信号与SVD降噪信号对比图Fig. 7 Comparison of original signal and SVD noise reduction signal

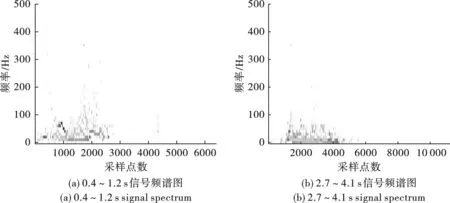
图8 原信号频谱图Fig. 8 Original signal spectrum

图9 SVD降噪后信号频谱图Fig. 9 Signal spectrum after SVD noise reduction

4 结论

(1)文中提出的LMD-MFE-SVD降噪方法具备一定的可行性和应用价值,通过计算MFE和进行SVD滤波能够对含噪的PF分量进行有效处理,提高整体的降噪效果。

(2)对于多信号成分、多种类噪声的仿真信号,LMD类算法相较EEMD、CEEMD、MEEMD算法降噪效率更高,SNR、RMSE和PRD的指标表现依次提升了71.62%、39.51%和35.71%,而相较LMD算法的降噪效率,提出的LMD-MFE-SVD算法也有明显改进,依次提升了11.73%、22.07%和9.25%,具备可观的信号降噪效率。

(3)根据实测松动爆破振动信号去噪后的波形和频谱对比,提出的LMD-MFE-SVD降噪后的信号波形更为集中,信号频谱图更为集中清晰,可以在消除噪声分量的同时保留原始信号的能量特征信息,对松动爆破振动信号降噪和松动爆破效应分析具有指导意义。