基于Fluent-EDEM流固耦合算法的水下台阶爆破爆堆形成过程研究*

吴 亮,余 创,梁志坚,段卫东,陈 明

(1.武汉科技大学 理学院 湖北省智能爆破工程技术研究中心,武汉 430065;2.武汉大学 水工岩石力学教育部重点实验室,武汉 430072)

众所周知,岩石的破碎和运动是岩土爆破中的2个关键环节,其中破碎块体的运动常被称抛掷运动。当实际生产中矿岩与普通岩互为夹层时,矿体运动结果对分离矿石和废石的影响较大,有时对采矿效率的影响远大于机械设备[1]。水下钻孔爆破作为工程爆破技术中的重要组成部分,广泛应用在扩展港口、疏浚航道、取水以及抢险救灾等工程中。水下与陆地岩石爆破的主要差异在于岩石表面接触介质的不同,直接影响了岩石的爆破破碎以及块体抛掷运动效果[2,3]。由于影响水下爆破效果的因素错综复杂,很多工程只能凭有关经验公式与试验数据估算,往往没有达到破碎与堆积效果;另外,室内的模型实验成本高且周期长,而现场试验无法及时获取水下爆破破碎与堆积效果,且很多工程也不具备现场试验条件。因此,水下爆破破碎与堆积效果的预测工作亟待解决。

由于爆破作用过程的复杂性,且现有数学模型还不完善或存在局限性,目前工程中对爆破效果的预测还主要依靠经验判断,其准确性及可靠性难以满足要求[4]。数十年来,数值模拟技术在爆破领域得到了广泛应用,但传统的连续介质模型很难对岩石爆炸冲击破碎后的块体运动进行模拟。YI采用颗粒模型(PBM)模拟了爆轰过程以及被爆的岩石等脆性介质[5],实现岩石爆破破碎过程,突破了连续介质模型难处理大变形的问题。PREECE结合并行计算技术采用三维离散元模型分析了数百个炮孔[6],离散单元数超过100万。安华明等采用有限—离散杂交元模拟了爆破漏斗产生的整个动态过程[7]。余德运等采用流体与DDA块体之间网格覆盖的流固耦合技术模拟了爆破漏斗形成过程[8]。苏都都等采用PFC 2D对爆破参数与爆堆形态的关系进行了研究[4],预测了台阶爆破的爆堆形态。冷振东等在岩体强度参数服从Weibull分布规律的基础上[9],采用3DEC离散元软件建立了台阶爆破的三维台阶爆破模型,模拟起爆位置对岩石的动态破碎与抛掷过程的影响规律。周旺潇等和YAN等在考虑不同区域块度尺寸分布的基础上[10,11],采用3DEC离散元模型讨论了的爆破漏斗与台阶爆破爆堆形态。可见,预测与控制爆破抛掷运动的数值软件的应用极大地提高了生产效率,但水下岩石爆破破碎及其抛掷运动目前鲜见报道。

近年来研究者开始采用CFD-DEM方法解决工程中的流固耦合问题,例如水下岩塞爆破和深海采矿管道固液混合流体[12,13]。XU等基于Fluent-EDEM耦合方法模拟了管道堵塞过程[14],通过考虑连续流体相和离散颗粒相,初步研究了水合物的堵塞机理。HE等基于Fluent-EDEM引入滑移网格[15],该模型可以同时分析大型实体模型自由移动引起的流场和小颗粒的运动。FU等采用CFD-DEM耦合的计算方法模拟了渗流力与掌子面岩体颗粒的相互作用[16]。WU等基于DEM中颗粒的接触模型[17,18],采用Fluent-EDEM耦合方法研究水下台阶爆破块体的运动过程及爆堆形态。随着计算软件的开发与应用,越来越多的研究者尝试采用各种数值计算的方法解决水下爆破的问题。因此,采用基于UDF开发的Fluent-EDEM耦合方法,考虑颗粒间的连接作用来研究水下岩石台阶爆破破碎及块体运动的问题,期望研究成果能促进水下台阶爆破技术发展。

1 计算方法

1.1 流体基本原理

计算流体力学是利用数学的计算方法来实现对流场中的控制方程进行计算,并对有限元网格节点进行数值求解。当研究对象为不可压缩流体时,基本的定律有三个:质量守恒定律、动量守恒定律、能量守恒定律,如下式(1)和式(2)。在本文中没有能量的交换,故不考虑能量守恒方程。

(1)

(2)

1.2 DEM颗粒接触模型

DEM模型中颗粒受力运动遵循牛顿第二定律,包括了转动和平动,颗粒的运动方程(动量守恒方程)如下式(3)和(4)所示。

(3)

(4)

式中:v、ω、m分别为颗粒速度、角速度和质量,下标i,j表示两个相互接触的颗粒;Fij为i和j颗粒间的接触力;Fg为颗粒间的引力;Ff为流体与颗粒间的相互作用力;I是颗粒转动惯量;T是颗粒间的力矩;Tf是流体引起的扭矩。

本文采用Hertz-Mindlin接触模型计算DEM颗粒之间的作用力,该模型具备滚动摩擦特性,如图1所示。Hertz-Mindlin接触模型的计算表达式见文献[19]。

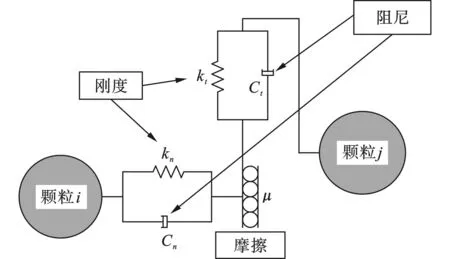
图1 Hertz-Mindlin接触模型示意图Fig. 1 Schematic diagram of Hertz-Mindlin’s contact model

1.3 DEM颗粒平行键模型

平行键模型(Parallel bond Model,PBM)可以用于模拟微观结构如何影响宏观行为,它将固体介质离散为具有固定尺寸的胶结颗粒材料,由于颗粒之间存在空隙,在固体介质模型形成平行键时,这些颗粒间的空隙可以视为混凝土材料中的自然孔隙或岩石中的自然裂缝,这些裂缝相互作用、合并形成宏观裂纹。平行键模型能表达颗粒间法向和切向的作用力,如图2所示,当法向或切向应力超过最大许可应力时平行键断裂,颗粒之间的相互作用回归到Hertz-Mindlin接触模型。

图2 平行键模型示意图Fig. 2 Schematic diagram of parallel bond model

在平行键生成之后颗粒上的力和扭矩被重置为0,在模型开始计算时则根据公式(5)～(8)在每个时间步长中计算平行键受到的力和扭矩的增量。

δFn=-vnSnAδt

(5)

δFt=-vtStAδt

(6)

δMn=-ωnStJδt

(7)

(8)

式中:Fn和Ft为法向力和切向力;Mn和Mt则为法向扭矩和切向扭矩;vn和vt为颗粒的法向和切向速度;ωn和ωt为法向和切向角速度;Sn和St为法向刚度和切向刚度;δt为时间步长;A是平行键截面面积,计算公式如式(9)所示;J为平行键截面极惯性矩,计算公式见式(10)。

(9)

(10)

式中:RB为平行键半径,是平行键合模型输入参数之一,取值一般大于颗粒半径。

当法向力或切向力超过其限定值时,颗粒间的平行键发生断裂

(11)

(12)

式中:σmax、τmax为最大法向应力和最大切向应力。

2 水下台阶爆破计算模型

2.1 计算模型

参考实际台阶爆破工程,数值模型中上台阶面距离水面10 m、台阶面宽6 m,台阶高度为10 m,炮孔直径0.105 m,孔深10 m,装药长度为7 m,堵塞3 m,孔间距为4.5 m,最小抵抗线为3 m。本文数值模型以单段4个炮孔同时起爆为对象进行建模,如图3所示。图3(a)为Fluent模型,上表面为压力出口边界,压力值设置为一个大气压。图3(b)为EDEM模型,颗粒填充区域为长23.5 m、宽5.5 m、高10 m的长方体,颗粒采用直径0.21 m的球形颗粒,共填充146728颗。

图3 计算模型(单位:m)Fig. 3 Calculation models in the numerical simulation(unit:m)

2.2 模型参数

在EDEM模型中引入平行键的模型来模拟连续的岩体介质,平行键的模型除了包含摩擦系数在内的基本力学参数外还需要额外输入5个平行键参数。由于平行键的模型能体现微观上颗粒之间的力学行为,除了平行键半径取颗粒半径值外,至今的研究结果还不能明确地给出实验中获得的参数与平行键参数之间的关系式,因此为了获得准确的数值计算参数,需对平行键的参数进行标定。许多学者使用DEM进行巴西劈裂数值计算[20-22],通过与实验结果对比,标定平行键的参数。

在EDEM中建立直径50 mm、高100 mm的圆柱模型,投放的球形颗粒直径均为3 mm,共投放颗粒8473颗,共生成平行键29 258个。分别对圆柱颗粒模型进行巴西劈裂数值模拟,模型破坏结果如图4(a)所示,应力-应变曲线如图4(b)。

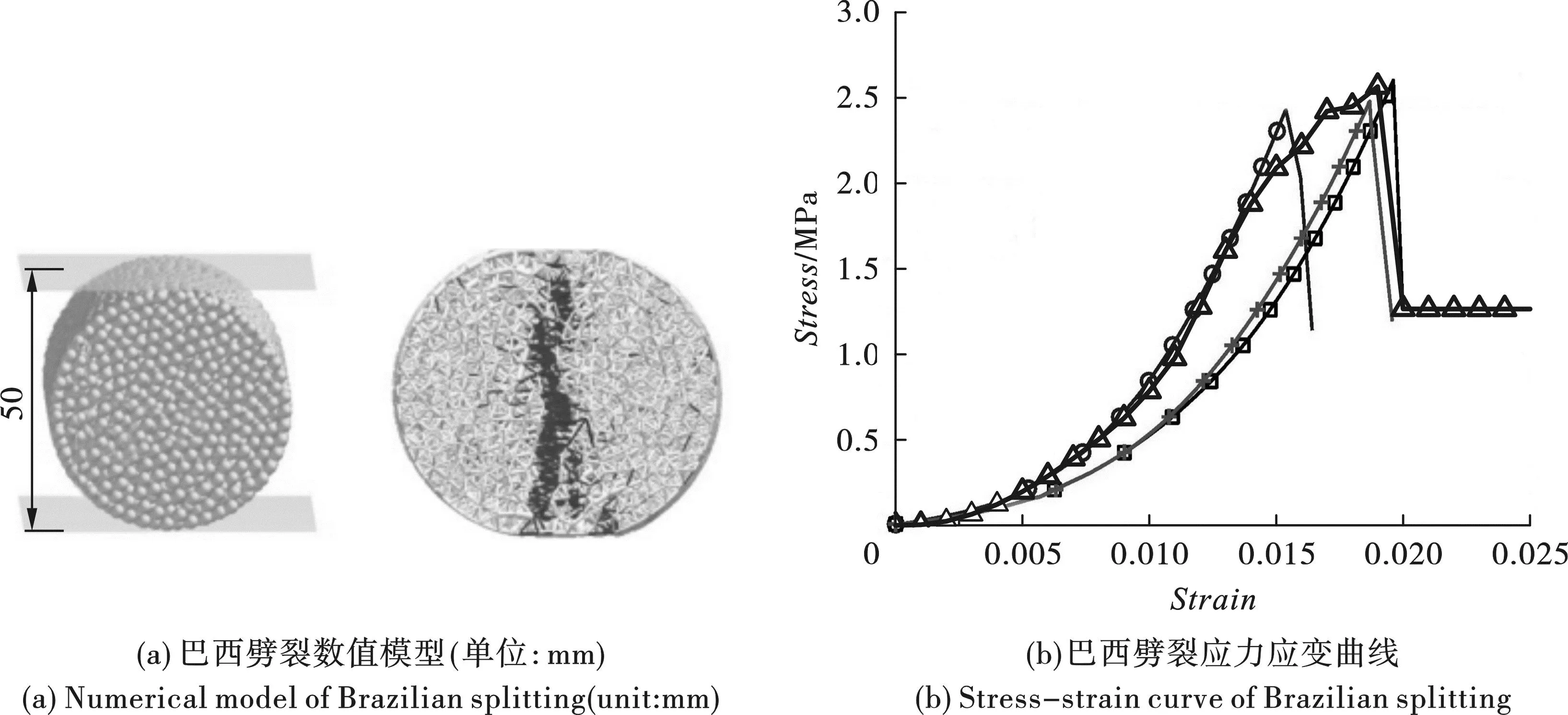
图4 巴西劈裂数值模拟Fig. 4 Numerical simulation of Brazilian splitting

图4(a)中灰白色为颗粒间的平行键,红色代表已破坏的平行键,巴西劈裂模型的破坏模式为拉伸破坏。图4(b)中三组巴西劈裂实验曲线来自文献[23]的实验。三组巴西劈裂实验的平均峰值应力为2.46 MPa,而数值模型的峰值应力为2.44 MPa。说明基于平行键方法建立的材料模型能够在一定程度上反映实际工况中岩石、混凝土等脆性材料的力学行为。

综上,结合标定后的平行键模型参数,将堆积的颗粒建立平行键,台阶模型共生成平行键351 460个,具体参数如下表1所示。需要注意的是,同一组模型中含有平行键与无平行键在时间步长的选取上存在差异,通常在进行含有平行键的数值模型计算时选取两者中时间步长较小的一个[24],本文离散元的计算步长为3×10-5s,流体的计算步长是离散元的10倍,为3×10-4s。

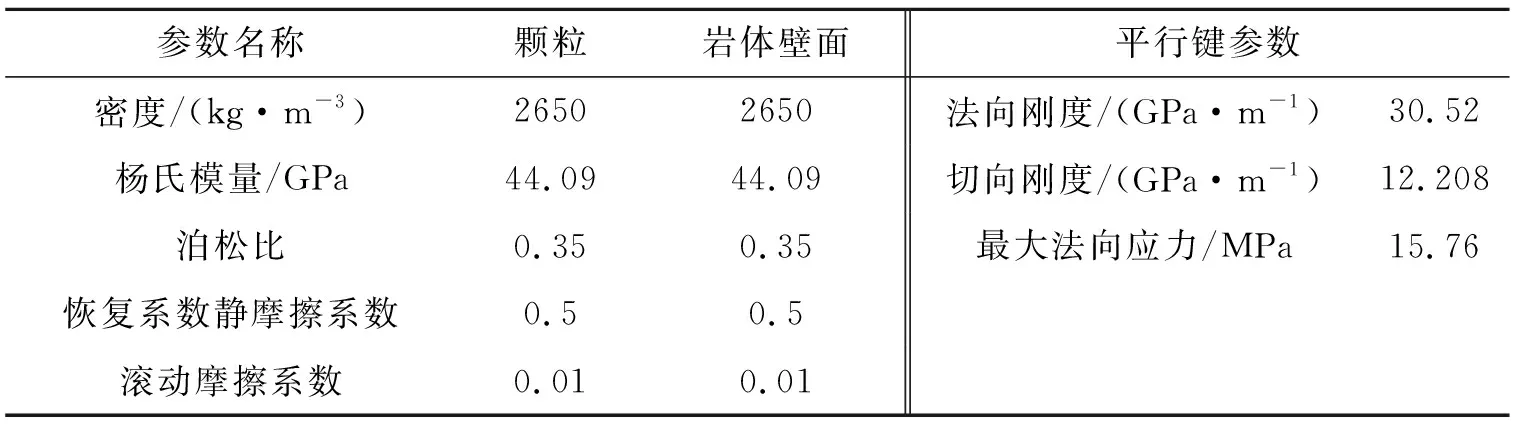
表1 岩体EDEM模型参数Table 1 EDEM model parameters of rock mass

3 模拟结果

3.1 台阶爆破破碎与块体运动过程

数值模型中通过在炮孔位置设置高压区域实现爆炸荷载的冲击作用,块体颗粒运动速度与未破坏的平行键分布图见图5,该图显示了在有平行键作用下水下台阶块体颗粒鼓包抛掷的整个运动过程。从台阶爆破破碎来看,初始状态颗粒间的平行键完整密布,炮孔内爆炸荷载作用在炮孔壁后,炮孔壁介质颗粒向外传递爆炸荷载并向外运动,当颗粒间的平行键超过临界值时将断开,处于炮孔附近的平行键大量破裂,结果显示平行键的断裂是从炮孔壁逐步向外开始扩散的。由于台阶颗粒排列是随机的,所以平行键断裂扩展到临水面时并不是一个平面,同时考虑应力波的反射作用,最先破裂的部位在炮孔的中部,该部位的块体颗粒获得的动能较多,所以抛掷的速度也最大,而台阶底部和上部的颗粒平行键的断裂滞后,特别是台阶上部以及两侧残存有大块。

图5 水下台阶爆破块体运动过程Fig. 5 Movement process of blocks underwater bench blasting block

从块体运动来看,在0.0204 s时刻,炮孔附近的块体颗粒速度明显大于两侧靠近岩体壁面的颗粒,说明鼓包运动由最小抵抗线方向开始。在0.492 s时刻,表面块体颗粒抛掷的速度峰值为2.48 m/s,随着颗粒进一步剥离表面,峰值速度持续增加。在0.918 s时,中部爆破区域呈现塌陷趋势,而两侧未见崩坏,部分颗粒在重力与浮力的作用下进行抛掷运动,并在3 s时刻颗粒抛掷速度峰值达到4.5 m/s,随后速度峰值逐渐衰减。在2.004 s时刻,可以明显观察到块体颗粒群形成了具有一定坡度的堆积体,此时块体颗粒的运动形式滚落为主。随着块体颗粒的继续滚动,块体颗粒在台阶前表面形成了平缓的爆堆,并伴随有左侧与堵塞段大块堆积在上面。

3.2 堆积范围和分层结果分析

为了方便观察台阶前方块体颗粒的堆积层次分布规律,将台阶前堆积的块体颗粒群选取并进行上色,底部颗粒为蓝色、中部颗粒为红色、上部颗粒为绿色,见图6(a)。图6(b)为水下台阶爆堆中间截面最终堆积形状的侧视图。通过侧视图测出爆堆堆积形状的休止角约为20°。爆后块体颗粒的分层延续了其在原台阶模型中的分布形式,块体爆堆中蓝色块体颗粒位于最下层、红色块体颗粒位于中间、绿色块体颗粒位于上层,且中部红色块体颗粒运动距离最远,中部红色块体颗粒覆盖了大部分的底部蓝色块体颗粒,主要原因是块体颗粒堆积分层与其初始速度和位置高度有关,台阶中部块体颗粒相对位置较高,在爆炸荷载作用下水平运动距离最远,而上部堵塞部分的块体颗粒受爆炸荷载作用小,其主要在重力与浮力作用下翻滚覆盖在中部块体颗粒层之上。

图6 块体颗粒堆积与分层效果Fig. 6 Range of accumulation and layered accumulation of blocks

3.3 块体运动速度和流体流场分析

为更具体地分析块体颗粒的堆积规律,在台阶前表面中轴线上选取6个测点,测点间距为2 m,每个测点均包含若干块体颗粒,见图3(b)所示,绘制颗粒的平均速度随时间变化的时程图,见图7,该速度方向垂直于台阶前表面。在炸药反向起爆之后,炸药起爆点位置处的2#和3#测点水平速度峰值最大,分别为3.4 m/s和3.0 m/s;位于底部的1#测点受到颗粒下沉碰撞影响,其峰值速度分别为2.1 m/s;台阶堵塞段的5#和6#测点的水平速度峰值曲线加速段斜率较低且到达最大速度峰值出现较晚,说明台阶堵塞段块体颗粒受爆炸荷载作用的强度较小,另外也说明该部分块体滚动滑落运动明显。随着块体颗粒的运动,颗粒的速度受水的阻力而衰减,在鼓包运动结束之后,块体颗粒以滚动滑落的运动形式为主。结合爆堆分层规律,并观察速度时程曲线后半段可知,块体颗粒的滚动滑落速度与其所处位置有关,位于底部的1#测点的块体颗粒由于受到底面的摩擦阻碍以及上层颗粒的覆盖作用,其块体颗粒的滑动速度较小,而4#～6#测点的滚动滑落速度随着高度的增加而衰减较慢。

图7 测点水平速度峰值时程曲线Fig. 7 Time history curve of horizontal velocity peak at measuring points

图8为台阶模型中轴面的流线分布图。起爆初期爆炸能量主要是破碎岩石,水体无明显流速,随着块体颗粒的鼓包抛掷运动,台阶前表面附近的流体流线速度最大。在2.0 s时刻台阶上部块体颗粒溃散滑落,导致了其表面附近出现流线回流。随着块体颗粒的滚动滑落形成具有平缓坡度的爆堆,流线的回流形式进一步扩大,但是流线的峰值速度在逐渐衰减。当块体颗粒开始滚动滑落时,流体流线则主要受到颗粒的运动形式影响,流线峰值速度区域均出现在块体颗粒附近。

图8 流线分布图Fig. 8 Streamline distribution diagram

4 结论

基于Fluent-EDEM耦合方法并采用平行键与Hertz-Mindlin接触模型模拟了水下岩体破碎和运动的力学作用机理,讨论了爆破块体抛掷速度、块体分层堆积和爆区流场特点,揭示了水下岩体爆破破碎块体堆积的运动特点。初步结论如下:

(1)水下台阶爆破块体颗粒堆积分层与其初始速度和位置高度有关,其本质是爆破能量密度分布与块体重力势能的外在表现。

(2)起爆初期爆炸能量主要是破碎岩石,水体无明显流速,随着块体颗粒的鼓包抛掷运动,最小抵抗线方向流体流线速度最大。当块体颗粒开始滚动滑落时,流线则主要受到颗粒的运动形式影响。

(3)采用平行键与Hertz-Mindlin接触模型能反映岩体爆破破碎过程,揭示大块产生的机理与范围。计算结果表明FLUENT-EDEM流固耦合的数值模型能较准确地模拟水下台阶爆破岩体破碎与块体运动问题,可为水下岩体爆破工程提供新的研究手段。