改进FCOS模型的微通道铝扁管表面缺陷检测算法

桂鹏辉，宋 涛，汤建斌，徐志鹏，曹松晓，蒋 庆

中国计量大学 计量测试工程学院，杭州 310018

微通道铝扁管为平行流微通道散热器的核心部件，由于生产工艺的限制，铝扁管表面会产生各类形态复杂的缺陷，导致其成品率较低。在工业生产中，铝扁管的表面缺陷识别由人工观测完成，该检测方案有着主观性强、效率低下、劳动强度高等缺点。对于铝扁管表面缺陷识别的任务而言，目前尚无高效准确的识别方案，因此，研究一种高效、精准的铝扁管表面缺陷识别算法对于提升其生产质量有着较高的价值。

近年来，随着计算机技术与深度学习技术的发展，基于深度学习的目标检测算法已经成为金属表面缺陷检测的主要技术之一。目前用于金属表面缺陷检测的算法主要有两类：以YOLO[1-4]系列、SSD[5]等模型为代表的一阶目标检测算法与以Faster R-CNN[6]为代表的二阶目标检测算法。如程婧怡等[7]通过使用K-means++[8]算法优化先验框参数，同时引入DIoU损失[9]计算回归误差的方式，提高了YOLOv3算法在金属表面缺陷检测上的检测精确率；李维刚等[10]通过改进YOLOv3架构的方法，更充分地混合骨干网络的浅层与深层特征，提高了模型对带钢表面细小缺陷的检测能力；代小红等[11]通过在Faster R-CNN 中引入ROI-Align[12]的方法，降低了检测框的位置偏移，提高了模型对金属工件表面的检测精度。以上目标检测算法的共同特征是依赖锚框，即通过人工设计或者统计多尺度多比例的锚框来对缺陷初步定位，然后由深度神经网络完成对定位后缺陷的回归与分类。在此过程中，大规模的锚框重复运算会消耗计算机的大量运算资源，降低检测速度，且模型的检测准确率对锚框的大小、长宽比等参数的设置非常敏感。

针对基于锚框的目标检测算法的局限性，近年来各种无锚框检测算法被陆续提出。无锚框检测算法直接使用关键点或像素点对物体的边框进行密集预测，从而规避与锚框相关的复杂运算，兼顾检测时的快速性与高精确率。全卷积一阶目标检测算法[13]（fully convolutional one-stage object detection，FCOS）是无锚框目标检测算法的典型代表之一，该算法通过特征图上的单个像素点判断物体种类，同时对其特征信息进行映射以得到物体的边框，并使用中心度分支（center-ness branch）来抑制低质量的回归框，使得模型在COCO数据集上取得了较高的检测精度。然而，当该算法应用于检测图1中存在的扁管表面狭长缺陷时，原始的正样本定义策略有概率遗漏这类缺陷，使模型在训练过程中忽略这类缺陷的损失，导致模型对狭长缺陷的漏检；此外，扁管表面的缺陷尺度范围广、长宽比变化大等特点也对FCOS的检测能力提出更高的要求。

图1 扁管表面的部分狭长缺陷Fig.1 Long and narrow defects on surface of flat tube

针对FCOS检测扁管表面缺陷的局限性，本文对该模型进行了以下几点改进：第一，设计一种特征卷积金字塔网络（feature convolutional pyramid network，FCPN）实现模型对骨干网络中多层特征的自适应分配；第二，改进模型的正样本部署策略，减轻FCOS对狭长缺陷的漏检；第三，结合第二步改进的正样本部署策略，设计改进的边框映射函数与中心度定义函数，进一步提高模型对狭长缺陷的检测能力；第四，替换原模型中的IoU 损失[14]，使用EIoU损失[15]更合理地计算模型的回归损失。

1 原始FCOS模型

1.1 FCOS原理简介

FCOS 为一阶无锚框目标检测算法，主要由骨干网络、特征混合网络以及目标检测网络三部分组成。FCOS使用ResNet50[16]作为模型的骨干网络来提取图像特征，随后通过特征金字塔网络[17]（feature pyramid network，FPN）对不同尺度的图像特征进行混合，得到5层可用于目标检测的混合后特征图。在训练过程中，FCOS 把特征图上落于标注框内且符合回归范围的点判为正样本，将其划分为标注框所属的目标种类，并将该点到标注框的4 个回归距离(l,t,r,b)作为回归目标，最终使模型在训练完毕后能依据特征图上的点来预测目标的位置与种类，如图2所示。

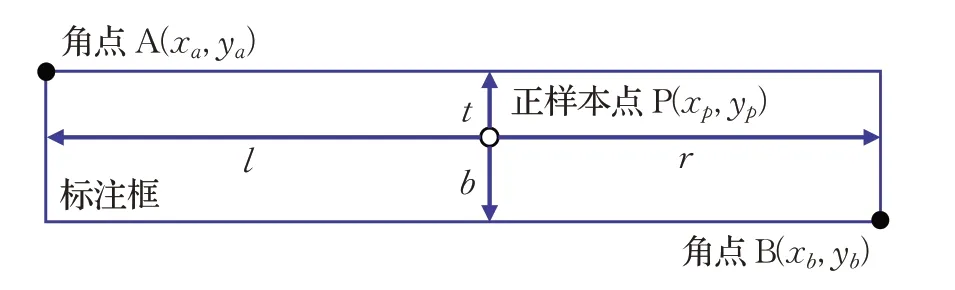
图2 正样本点回归示意图Fig.2 Regression schematic diagram of positive sample point

在图2 中，A、B 两点为组成矩形标注框的两个角点，(l,t,r,b)为正样本点P到标注框左、上、右、下四条边的距离，即FCOS在训练时的回归目标，这4个回归目标可由A、B 两个角点的坐标和正样本点P 的坐标计算得到，计算过程如式（1）所示：

式（1）中，(xa,ya)T为边框左上角点A的坐标，(xb,yb)T为边框右下角点B的坐标，(xp,yp)T为正样本点P的坐标。

1.2 原始FCOS的局限性

原始FCOS模型根据5层特征图的像素感受野范围在输入图像中分别部署间距为{8，16，32，64，128}的5种网格点，并将落于标注框内的网格点作为能够代表物体的候选正样本点。为合理地将不同间距的候选点部署到相应的特征层中，模型根据式（2）对候选点进行回归距离限制，并将相应回归范围内的候选点作为正样本划分给对应的特征层。

式（2）中，mi是第i层特征图的最大回归距离上限，mi-1是第i层特征图的最大回归距离下限，FCOS 将m2～m7分别设置为{0,26,27,28,29,+∞}。

FCOS在式（2）的限制下，将不同间距的候选点划分给相应特征层虽然能有效利用各尺度特征图，实现目标的多尺度检测，但是当图像样本中出现狭长缺陷时，这种正样本部署策略仍然有可能造成这类物体的漏检，如图3所示。

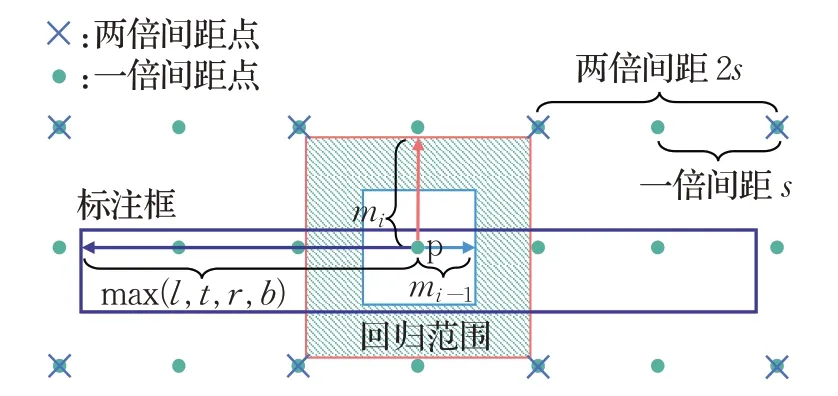
图3 网格点部署示意图Fig.3 Deployment schematic diagram of grid points

图3 中部署了任意两种间距相差两倍的网格点。其中两倍间距点均落于标注框外，可直接排除；部分一倍间距点落于标注框内，可作为候选正样本点。以其中任意一点p为例，该点到边框的最大回归距离max(l,t,r,b)超出了p点由(mi-1,mi)所划定的回归范围限制，也被判为负样本，因此标注框内的所有一倍间距点均被判为负样本，即标注框内没有任何正样本点可用于FCOS模型的训练，使模型在预测过程中对该缺陷漏检。模型的实际正样本部署情况如图4所示。

图4 标注框内的正样本点分布图Fig.4 Positive sample point distributions in label boxes

在图4中，虽然部分标注框中分布着不同间距的正样本点，但是在一些狭长缺陷的标注框中并不存在任何的正样本点，使模型在训练过程中排除了这些显而易见的长条缺陷，并未考虑其训练损失，最终导致对这类狭长缺陷的漏检。

此外原始FCOS使用FPN混合各层特征图，以提高模型对不同尺度缺陷的检测能力，但是FPN对于不同层特征图的混合方式为线性累加，模型不能自适应地挑选各层特征进行检测。针对原始FCOS模型的以上不足，本文设计了一系列改进，将在第2章进行详细论述。

2 改进的FCOS模型

2.1 改进后的模型架构

本文模型以FCOS为基础，针对扁管表面的缺陷检测任务，分别从设计特征卷积金字塔网络、改进正样本部署策略、改进边框回归函数与中心度定义函数这三点对FCOS模型进行了更改，并将IoU损失替换为EIoU损失，以更合理地计算模型的回归损失。改进后的FCOS模型如图5所示。

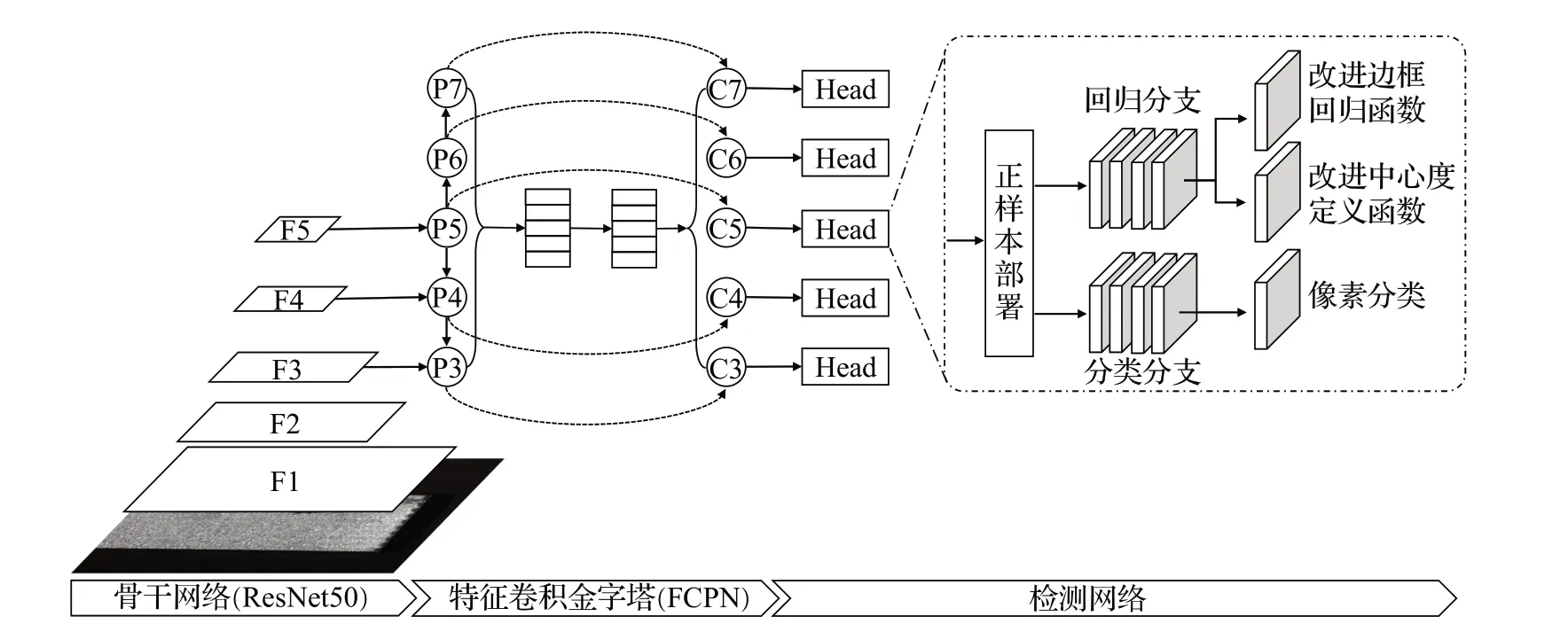
图5 改进后FCOS模型Fig.5 Improved FCOS model

在图5 中，改进后FCOS 模型首先使用ResNet50 提取扁管样本图像中的特征信息，得到特征图F1～F5；随后使用特征金字塔初步混合特征图F3～F5，得到P3～P7；接着P3～P7 被送入特征卷积金字塔网络（FCPN），实现不同层特征信息的自适应混合，得到特征图C3～C7；最后使用改进后检测网络对特征图中的正样本像素进行中心度回归、边框回归以及种类划分。下文将对改进的各部分进行详细分析。

2.2 特征卷积金字塔网络

原始FCOS 模型使用FPN 混合骨干网络提取的各层特征图，以提高模型对不同尺度缺陷的检测能力。但是FPN 对各层特征图之间的混合方式为按像素线性相加，无法实现各层特征图的自适应选取与分配，且无法提取特征间的相关性信息。针对FPN的这一不足，本文设计了一种特征卷积金字塔网络（FCPN），FCPN的结构如图6所示。

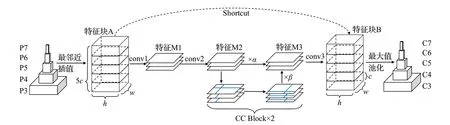
图6 特征卷积金字塔网络（FCPN）Fig.6 Feature convolutional pyramid network（FCPN）

在图6 中，P3～P7 为特征金字塔初步混合后的特征图。首先使用最邻近插值对P3～P7分别进行{1，2，4，8，16}倍上采样，并在通道维对采样后特征进行拼接，得到特征块A，大小为5c×h×w；其次由两次3×3 卷积实现特征块A上不同尺度特征图的初步混合，得到特征M1、M2；为了提取像素间的相关性特征，提高模型的检测能力，本文在特征M2的旁路引出一个自注意力分支，使用两个十字交叉注意力模块[18]（criss cross block，CC Block）对混合后特征M2进行注意力筛选；然后由系数α、β对M2与注意力特征进行权重分配，再逐元素相加，得到混合了特征块A 之间各层信息与像素间相关性信息的特征M3，系数α、β由模型在训练过程中自适应搜寻，初始值分别定义为0.5、0.5，且满足约束条件α+β=1,α∈[0,1]；接着对M3使用一次3×3卷积得到大小为5c×h×w的特征块B，并且在特征块B与特征块A之间引入残差连接，降低模型的过拟合风险；最后使用深度为c的最大值池化对特征块B分别进行{1，2，4，8，16}倍下采样，得到特征C3～C7。FCPN中3次卷积操作的结构参数如表1所示。

表1 FCPN的3次卷积参数表Table 1 Convolutional parameters of FCPN

在表1 中，每组卷积操作后都进行了群组标准化[19]（group normalization，GN）与ReLU[20]激活，目的是降低传播误差、实现对特征块A不同特征层之间的非线性混合，以得到特征块B。由于这两层无需设置与卷积相关的参数，因此在表格中均以符号“×”表示。

相比于FPN 网络，特征卷积金字塔（FCPN）可以在前向传播中由三次卷积与两个十字交叉注意力模块完成不同层特征图的通道间、像素间的自适应特征提取与混合，因此能够提高FCOS模型的检测能力。

2.3 改进的正样本部署策略

由1.2 节分析可知，原始FCOS 对狭长缺陷的漏检主要是由于模型只能在标注框内部挑选指定回归范围内的网格点作为正样本点导致的。针对该问题，本文改进了原始模型中正样本部署策略的限制条件，降低了模型对狭长缺陷的漏检概率。

原始正样本部署策略由两个限制条件构成：第一，正样本点必须落于标注框内部；第二，不同间距的正样本点必须满足对应特征图的回归距离限制。考虑到第二个限制条件能够有效利用不同感受野的特征图进行多尺度目标检测，不宜更改，故本文将替换第一个限制条件：将与标注框几何中心的间距为指定范围内的网格点作为候选正样本点，如式（3）所示：

在式（3）中，dx、dy分别为网格点与几何中心的横、纵坐标间距，k为间距缩放倍数，本文将k设为1.5，si为网格间距，si∈{8,16,32,64,128}。由式（3）筛选后确定的候选点没有必须落于标注框内部的限制，而是选择与标注框几何中心间距小于1.5倍si的网格点作为正样本候选点。式（3）允许模型将落于标注框外一定距离范围内的网格点作为正样本参与检测任务的训练，从而降低模型对狭长缺陷的漏检概率。

由式（2）、式（3）改进的正样本部署策略在含有狭长缺陷的实际图像中的部署情况如图7所示。

图7 改进部署策略的正样本分布图Fig.7 Positive sample distribution diagram of improved deployment strategy

由该图可知，改进后的正样本部署策略在图7的狭长缺陷周围选择9个正样本点用于目标检测任务，该策略避免了在图4 中展示的狭长缺陷无正样本点可用的问题，使模型在训练过程中不遗漏狭长缺陷的相关损失，因此能够提高模型在扁管表面缺陷检测任务中的准确性。

2.4 改进边框映射函数与中心度定义函数

2.4.1 改进的边框映射函数

原始FCOS 模型部署的正样本点全部位于标注框内部，此时其回归目标(l,t,r,b) 均大于0，因此当原始FCOS 模型使用映射函数exp(⋅)进行边框拟合时，能够达到较好的拟合程度，使模型在正常比例物体的检测任务中，能够达到较高的检测精确率。

但是映射函数exp(⋅)仅能将特征图上的像素特征映射为正数，当本文改进原始模型的样本部署策略后，正样本点可能会落于狭长标注框的外界，此时必定存在一个回归距离小于0，使exp(⋅)无法对该点进行正确的映射，如图8所示。

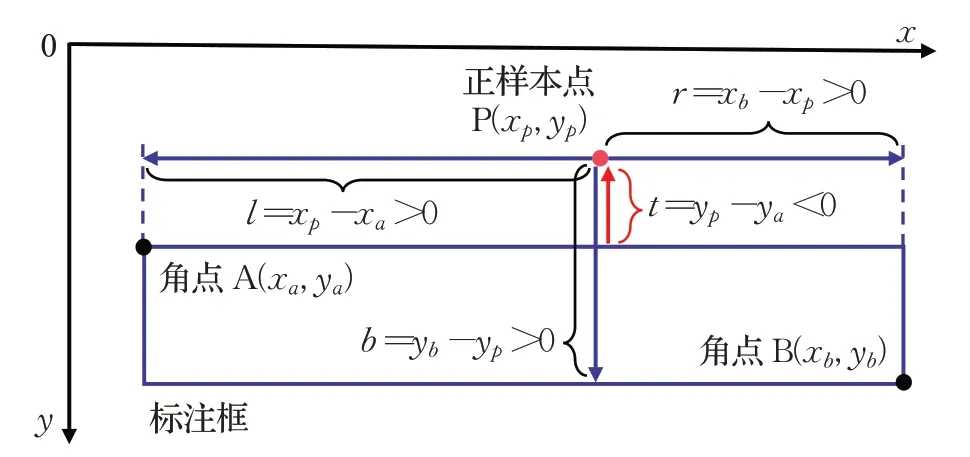
图8 回归距离小于0的情况Fig.8 Situation of regression distance is less than 0

为了使正样本落于边框外时仍能对边框进行有效的映射，本文舍弃了原始FCOS 模型中的映射函数，而是参考FCOSv2[21]模型的回归函数，并结合本文改进后的正样本部署策略，设计了改进后的边框映射函数，如式（4）所示：

在式（4）中，σ为激活函数，qi为映射函数在每个特征层的缩放系数，该值由FCOS模型在训练中自适应搜寻，x为由卷积操作提取到的特征点数值，si为网格间距，同式（3）中的si。本文使用ELU[22]函数作为式（4）中的激活函数σ，该函数图像如图9所示。

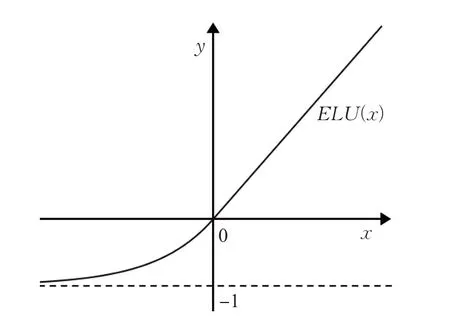
图9 ELU函数Fig.9 ELU function

由图9 可知，ELU 的值域范围为(-1,+∞)，因此该函数能够将qi×x映射为负数，能够对位于标注框外部的正样本点进行有效映射，避免了原始映射函数无法回归负数的问题，提高模型的检测精确率。

2.4.2 改进的中心度定义函数

相比于其他全卷积目标检测算法，FCOS 认为越靠近标注框几何中心的样本的回归准确率越高，因此该模型的主要创新点在于提出了“中心度分支（center-ness branch）”这一该概念来衡量每个正样本点的回归质量：在预测每个样本点的中心度后，滤除中心度低的样本，再对剩余的高质量样本进行非极大值抑制以得到最终的检测目标。在原始FCOS 模型中，center-ness branch的回归目标：中心度定义函数可由式（5）描述：

由式（5）可知，当网格点位于标注框外的上、下、左、右四个方位时，此式求得的中心度为虚数，当网格点位于标注框外的左上、左下、右上、右下四个方位时，其中心度又出现逐渐增大的趋势。即式（5）的计算方法只能正确衡量落于标注框内部的正样本点的中心度。对于在图7中所展示的，位于标注框外部的正样本点的中心度则无法正确衡量。

因此本文为了有效衡量位于标注框外部的正样本点的中心度，设计了改进后的中心度定义函数，如式（6）所示：

式（6）所定义的中心度函数的取值上下限与式（5）一致，分别为1、0，且当样本点越靠近标注框几何中心时，取值越接近1，越远离几何中心时，取值越接近0，并且未给模型引入额外的超参数。因此式（6）满足作为中心度定义函数的要求。原始中心度函数与本文设计的中心度函数的对比如图10所示。

图10 式（5）、式（6）的两种中心度曲面Fig.10 Two center-ness curved surfaces of formula（5），formula（6）

在图10 中，虚线矩形为缺陷的人工标注框。由该图可知，对于部署在标注框外的网格点中心度，式（5）所定义的原始中心度函数的计算结果明显有误，而由式（6）定义的改进后中心度函数，则能够准确地衡量标注框内外的所有网格点的中心度。

2.5 回归损失函数

原始FCOS 模型中的回归损失由IoU 损失函数计算，无法有效指示预测框的长宽与角点的回归方向，且当预测框与标注框没有交集时，IoU损失为常数1，此时与该预测框相关的参数梯度为0，无法进一步更新模型中相关的参数。因此本文使用EIoU 损失代替原先的IoU损失函数，将其用于计算边框的回归误差，如式（7）所示：

其中，IoU（intersection over union）为预测框与标注框的交并比，dc、W、H分别为包围预测框与标注框的最小外接矩形的对角线距离、宽与高，o、ogt、w、wgt、h、hgt分别表示预测框与标注框的中心坐标、宽和高，ρ2表示两者间欧式距离。该损失函数避免了原先IoU 损失的缺陷，将预测框与标注框之间的中心点间距与长宽间距纳入了损失的计算之中，能够更合理地计算预测框与标注框之间的回归误差。

3 实验与分析

3.1 样本预处理

本文的图像样本均采集自铝扁管生产现场，图像宽高为548×1 000。采集到的样本共可以分为5 类，分别为：污渍、凹坑、锌渣、整体、划痕。本检测任务的缺陷类别定义和样本如图11所示。

图11 缺陷样本图Fig.11 Samples of defects

在采集的样本图像中，需要剔除部分成像质量较差或者没有缺陷的样本，剩余1 247 张样本可用于缺陷检测，并划分其中80%的样本作为训练集，20%的样本作为测试集。为进一步提高改进后FCOS 模型的鲁棒性与检测精确率，本文在训练过程中对扁管数据集进行了在线随机数据增强，共有以下5种增强方式：翻转、平移、改变亮度、添加高斯噪声、添加椒盐噪声，如图12所示。

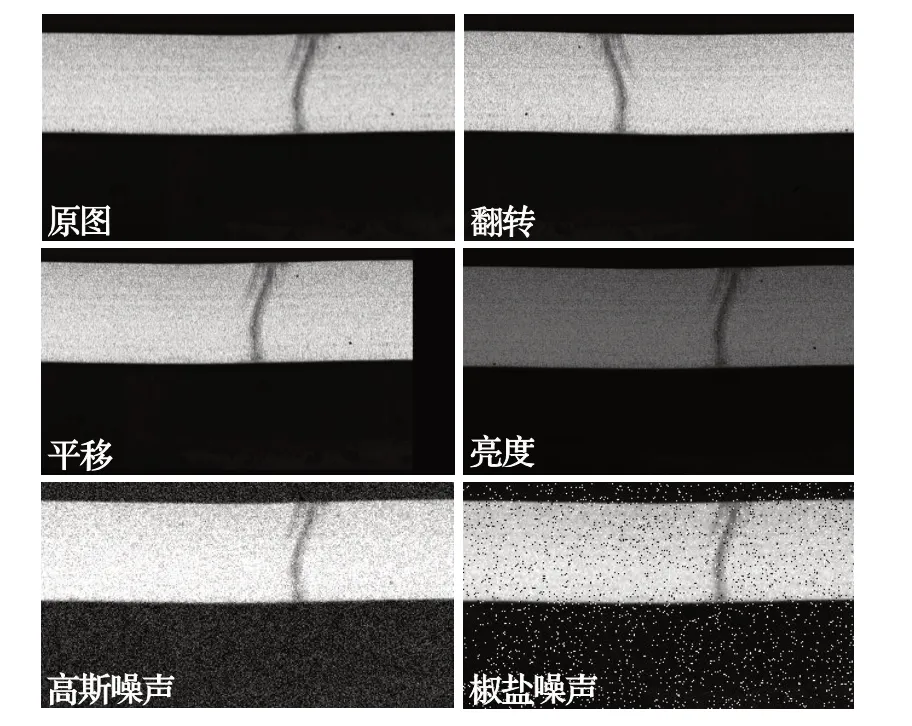
图12 本文的图像增强方法Fig.12 Image enhancement methods of this paper

3.2 评价指标

在目标检测模型中，一般使用平均精确率（average precision，AP）衡量模型对单一种类目标的检测能力，其计算方法如式（8）所示：

其中，P、R分别表示在指定的交并比阈值下，模型对单一种类目标的检测精准率与召回率。由单类目标的AP值，可定义各项平均精确率均值（mean average precision，mAP），如式（9）所示：

式（9）中，n表示数据集中的物体种类数。AP 与mAP是衡量模型对数据集内的单一种类目标与所有种类目标的检测能力的重要评估指标，这两个指标的取值范围为0～1，越接近于1，说明模型的检测能力越好。

3.3 实验平台与超参数设置

本文所使用的实验平台配置为：RTX3090 显卡、AMD3950x 处理器、内存频率为3 000 MHz，模型基于pytorch1.10搭建，使用CUDA 11.3.1加速。在训练过程中，模型的batch size为16，图像高宽为1 000×548，采用Adam 优化器更新模型的权重与偏置，在训练之前预热1 轮，随后采用余弦退火开始正式训练，初始学习率为0.000 1，共训练160轮。

3.4 训练结果与数据分析

3.4.1 模型对比与分析

使用以上超参数设置的模型在扁管表面缺陷检测任务中的训练结果如图13所示。

图13 改进后FCOS的训练过程曲线Fig.13 Training process curve of improved FCOS model

在图13 中分别展示了改进后FCOS 模型的总损失变化曲线与测试集的mAP（IoU=0.5）曲线，由该图可知，模型在训练到7 300 步左右时总损失不再明显变化，稳定在0.66左右，此时模型的mAP也已稳定，没有进一步变化的趋势，约为0.764。

为了验证本文改进后模型的检测能力，本文将原始FCOS 模型、FCOS v2 以及本文改进后的FCOS 模型进行了检测性能的对比实验，实验结果如表2所示。

表2 三种FCOS模型的检测性能对比Table 2 Comparison of detection capability of three FCOS models

由表2 可知，当IoU 为0.5 时，本文改进后模型的mAP 比原始FCOS 模型提高了7.7 个百分点，比FCOS v2提高了3.1个百分点；当IoU为0.75时，本文改进后模型的mAP比是原始FCOS模型提高了15.7个百分点，比FCOS v2提高了2.8个百分点；当IoU从0.5变化到0.95时，其mAP 均值为59.3%，比原始FCOS 模型提高了13.2 个百分点，比FCOS v2 提高了3.9 个百分点。由此可知，相比于原始FCOS 和FCOS v2 两个模型，本文针对扁管表面缺陷检测任务而改进的模型有着更好的检测能力。

为更进一步验证模型中改进的各部分在扁管表面缺陷检测任务中的有效性，本文进行了相应的消融实验，实验结果如表3所示。

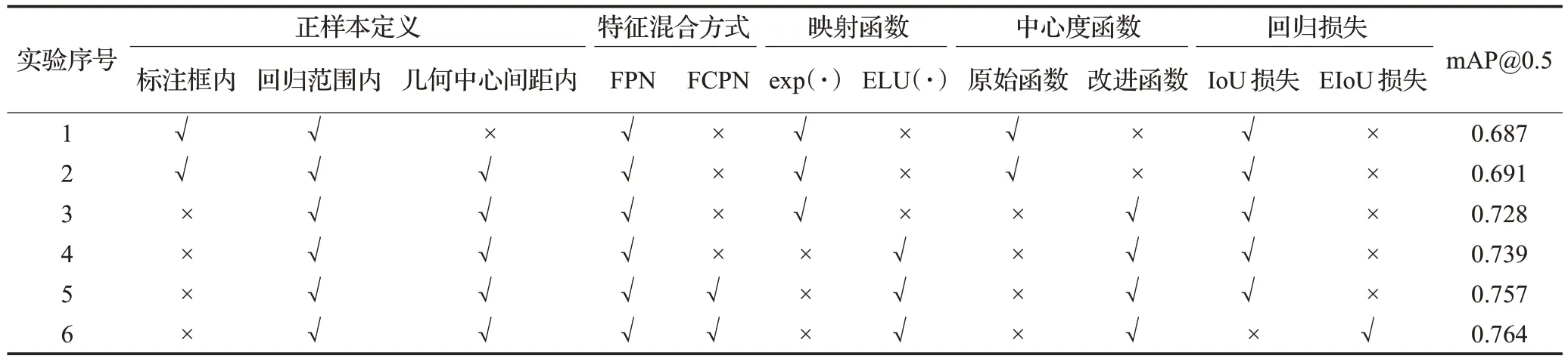
表3 对各部分改进的消融实验Table 3 Ablation experiments of each improved parts

在表3 中，本文使用mAP@0.5 衡量使用相应改进部分的FCOS模型的检测能力，在实验1中，模型并未采取任何改进措施，为原始FCOS，此时mAP 为68.7%；在实验2 中，本文将正样本点限制在标注框内、回归范围内以及几何中心点的间距内，此时mAP有略微提升，为69.1%；在实验3 中，仅使用回归范围内、标注框几何中心间距内两个条件限制模型的正样本点，此时正样本点可能落于标注框外部，因此使用了改进的中心度函数定义每个样本点的中心度，此时模型的mAP 为72.8%，比原始模型提升4.1 个百分点；相比于实验3，实验4 将回归函数由exp替换为了ELU，此时落于标注框外部的正样本也能准确参与边框的回归，mAP 为73.9%，提升了5.2个百分点；在实验5中引入了本文设计的特征卷积金字塔网络（FCPN），该网络能够在训练过程中自适应混合FPN上不同大小的特征图，并使用十字交叉注意力模块提取像素间的相关性信息，提高模型的检测能力，引入FCPN后的模型mAP为75.7%，提升了7.0个百分点；最后，实验6将IoU回归损失替换为EIoU损失，EIoU损失能够将预测框与标注框之间的中心点距离与长宽距离纳入模型的总损失中，进一步缩小预测框与标注框之间的差距，使改进后模型的mAP 达到76.4%，比原始模型提升了7.7个百分点。

3.4.2 FCPN的结构验证与特征可视化

为验证设计的FCPN网络结构的合理性，本文就表3中实验6引入的FCPN网络是否采用残差结构（shortcut），是否使用十字交叉注意力模块（CC Block），以及使用不同的上、下采样模式等策略分别进行了实验筛选。筛选结果如表4所示。

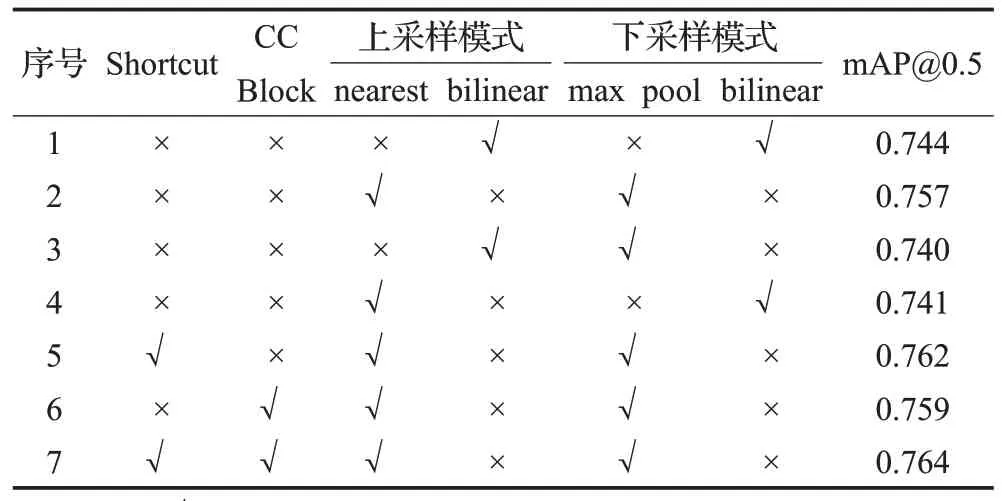
表4 FCPN中不同策略对FCOS检测结果的影响Table 4 Influence of different strategies in FCPN on FCOS detection results

在表4中，实验序号1～4用于筛选最合适的上、下采样策略，由实验2 可知，当上采样策略为最邻近插值（nearest），下采样策略为最大值池化（max pool）时，改进后模型可获得最佳的检测效果，此时mAP@0.5为0.757。实验序号5～7 用于筛选是否引入残差结构（Shortcut）与十字交叉注意力模块（CC Block），由实验7可知，当FCPN在实验2 的基础上，再引入Shortcut 与CC Block 时，FCOS模型的mAP@0.5提升到最大值，为0.764。

为直观展示FCPN网络的特征混合与提取能力，本文在表4 中实验7 的基础上，参考Eigen CAM[23]绘制了FCPN 混合前后的特征块A、B 的激活热力图，如图14所示。

图14 标注图像与特征块A、B的激活后热力图Fig.14 Marked images and activated heat maps of feature block A，B

在图14中，第一行为人工标注样本，第二行为FPN混合得到的特征块A的热力图，第三行为在FPN后再使用FCPN混合得到的特征块B的热力图。在热力图中，像素越趋于红色表示模型对该像素的响应越敏感，像素越趋于蓝色表示模型对该像素的响应越迟缓。由图14可知，特征块A 除了对扁管表面缺陷区域有响应之外，对于非缺陷区域的像素也有着不同程度的响应，这一点在该图的6～8列尤为明显：特征块A对不存在扁管信息的背景区域做出了错误的积极响应。相较于特征块A，特征块B对缺陷的响应则更加集中和明显，并且能够更好地滤除非缺陷区域的响应噪声。由热力图差异可知，在FPN后引入FCPN能够更合理地混合、提取特征图上的特征信息，提高模型的检测精确率。

3.4.3 不同映射函数的对比实验

由于本文使用ELU函数对落于标注框外部的样本点的负回归距离进行映射，因此能够利用这些样本对高长宽比的狭长缺陷进行回归。为验证ELU函数的有效性，本文在表3 中实验6 的基础上，选择了exp、ReLU、Leaky ReLU[24]以及最终采用的ELU这几种函数分别进行了对比实验，实验结果如表5所示。

表5 不同映射函数的mAP对比Table 5 Comparison of mAP of different mapping functions

由表5可知，由于exp与ReLU两个映射函数的值域始终大于0，模型在训练时无法回归位于标注框外的正样本，因此两者的mAP 较低；Leaky ReLU 与ELU 两个函数的值域分别为整个实数域R、(-1,+∞)，因此相比于前两个函数，Leaky ReLU与ELU能够更好地映射落于标注框外的正样本，其mAP也更高。将Leaky ReLU与ELU 分别作为式（5）中的激活函数σ时，模型检测精确率的差距并不明显，但总体来说，当激活函数选择ELU 时，模型的mAP@0.5 与mAP@0.5：0.95 略高一些，因此本文在式（5）中使用ELU 作为最终的激活函数σ。为更直观地展示改进后模型选择exp、ReLU、Leaky ReLU、ELU进行映射的区别，本文对分别采用这四种映射函数训练的改进后模型的检测结果进行了可视化，如图15所示。

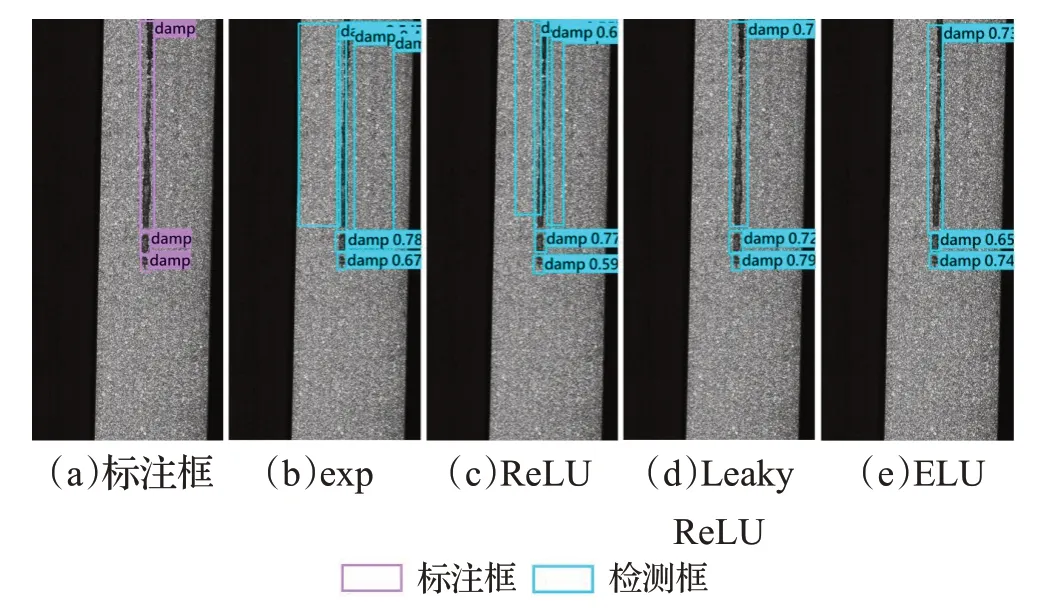
图15 使用四种映射函数的改进后模型的检测结果Fig.15 Detection results of improved models using four mapping functions

由图15 可知，若使用不含负部的exp 与ReLU 函数作为映射函数，则改进后模型在训练中无法正确映射标注框外部正样本点的负回归距离，而这类位于标注框外部的正样本点更有可能代表狭长的缺陷，因此在预测时，模型在狭长缺陷周围预测了错误的检测框；而使用含有负部的Leaky ReLU与ELU函数作为映射函数时，改进后模型能够在训练中正确映射落于标注框外部的正样本点的负回归距离，因此预测的结果更加准确。

3.4.4 改进后中心度函数与样本部署策略对模型的影响

模型训练时，改进的样本部署策略会产生标注框外的正样本点，因此本文设计了改进的中心度函数（式（6）），以计算这些样本点的中心度，指引中心度分支的回归。在预测阶段，模型可以结合中心度估值，滤除偏离中心的候选框，从而提高模型的检测精确率。

为比较本文提出的样本部署策略与中心度函数及原始方法对模型检测能力的影响，在图16 中分别绘制了使用不同方法训练模型后得到的P-R曲线。

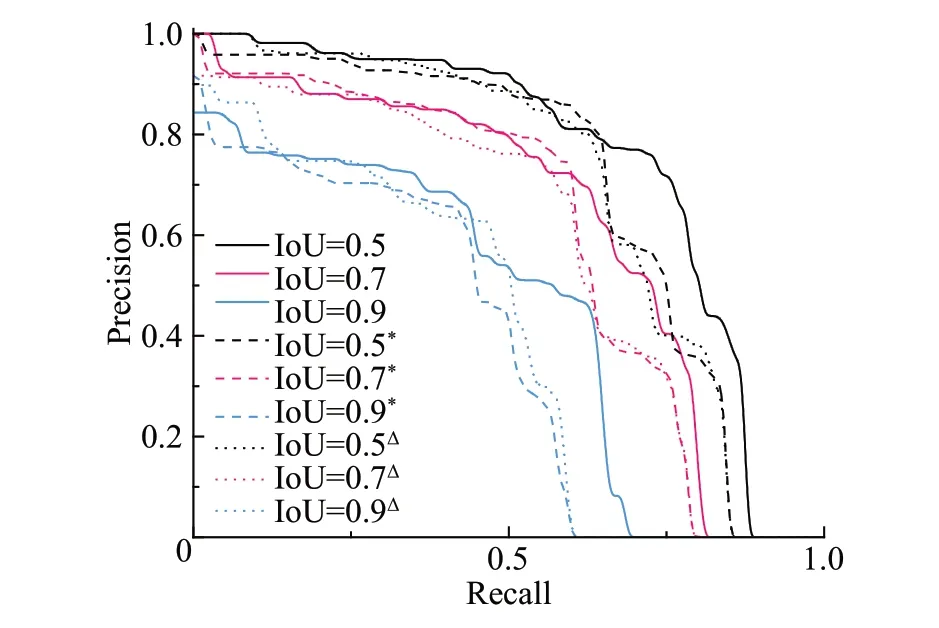
图16 不同方法训练模型后得到的P-R曲线Fig.16 P-R curve obtained after training model with different methods

在图16中，依据IoU的不同取值（0.5、0.7、0.9）分别绘制了三组P-R 曲线，每组曲线可进一步分为三种，分别为：使用本文方法训练模型后的P-R 曲线（实线）、使用原始方法训练模型后的P-R 曲线（点线，图例中以上角标“Δ”标出）、使用本文方法训练但不滤除低中心度特征点的模型的P-R曲线（短划线，图例中以上角标“*”标出）。在图16 中，三组IoU 取值范围下的实线均不同程度地包裹了点线，说明与原始方法相比，本文改进后的样本部署策略和中心度函数在同等精确度下能获得更好的召回率；此外，在不同IoU 取值范围下的实线与坐标轴的包围面积也均大于短划线与坐标轴的包围面积，说明滤除低中心度特征点能够对本文改进后模型的检测精确率的提升有积极影响。为定量分析改进前后的方法以及是否滤除低中心度特征对模型的影响，本文计算了图16 中不同曲线的积分面积（即模型mAP），计算结果如表6所示。

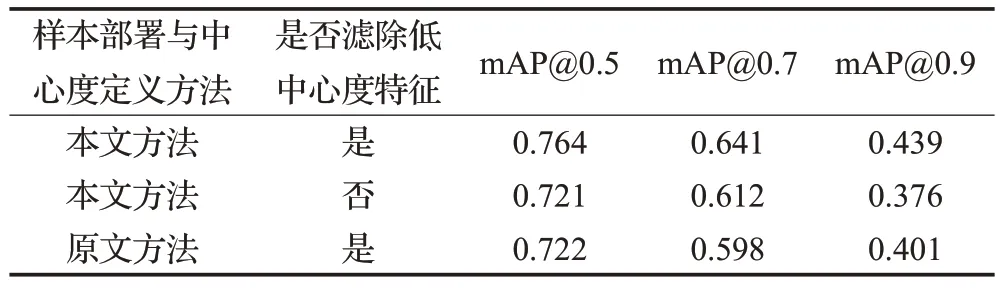
表6 三组P-R曲线的mAP值Table 6 mAP values of three sets of P-R curves

由表6 可知，与原文方法相比，在滤除低中心度特征后，本文的改进方法在三组不同的IoU阈值下均使模型取得了更高的mAP，说明本文方法能够使模型在扁管表面缺陷检测任务上获得更好的检测结果。

3.5 图像测试与分析

为对检测结果进行直观的验证与分析，本文对原始FCOS模型以及改进后FCOS模型在扁管表面缺陷测试集上的部分检测结果进行了可视化，检测结果如图17所示。

图17 原始FCOS与改进后FCOS模型的检测样本对比图Fig.17 Comparison chart of detection results between original FCOS and improved FCOS model

在图17中，紫色框人工标注样本，蓝色框为模型的正确检测结果，橘色框为误检缺陷，黄色框为漏检缺陷。从图17的第5～9列可以看出，原始FCOS模型未能检出其中的狭长缺陷，而本文改进后的模型由于使用了改进的样本部署策略，并设计了相应的中心度函数与映射函数，因此能够将这些狭长缺陷检出。此外，由于本文改进的模型使用了能分配自适应特征层的FCPN 网络，更加适应物体的尺度变化。因此在图17 的第2、7、8、9列可以看出，本文模型对于细小缺陷的漏检更少，且从该图的第3列可以看出，本文模型对大尺度缺陷的边框回归更加准确。从该图的第4、8列可以看出，本文改进后模型的误检情况也更少。

4 结语

针对扁管表面缺陷检测问题，本文提出了一种改进的FCOS 算法：首先设计特征卷积金字塔网络（FCPN）用于自适应地分配不同层特征图之间的特征信息，提高模型对多尺度缺陷的检测能力；其次改进模型的正样本部署策略，提高模型对狭长缺陷的检测能力；然后设计了改进的中心度定义函数与边框回归函数，以合理计算落于标注框外部的正样本点的中心度与回归值；最后使用EIoU 损失替换原始模型中的IoU 损失，将回归目标的长、宽以及中心点间距纳入总体的回归损失之中，从而在原始模型的基础上，进一步提高改进后模型对狭长缺陷的检测能力。

在消融实验中，验证了模型的各部分改进措施在一定程度上提高了模型的检测能力；在FCPN的结构验证与特征可视化实验中，验证了FCPN 各模块的合理性；在映射函数的对比实验中，证明了当样本点位于标注框外部时，使用具有负部的激活函数能够使模型获得更好的检测结果；此外，改进后样本部署策略与中心度函数能够比原始方法获得更高的检测精确率。

实验结果表明，当IoU取0.5时，本文改进后的FCOS模型在扁管表面缺陷检测任务上的mAP为76.4%，比原始FCOS模型提高了7.7个百分点。