基于γ宽束衰减的方位密度测井间隙计算及应用

于华伟 张倩文 王哲 罗琳 刘睿 于其蛟 杜海洋 韩春田

1（深层油气全国重点实验室（中国石油大学（华东）） 青岛 266580）

2（中国石油大学（华东）地球科学与技术学院 青岛 266580）

3（中国石油大学（华东） 档案馆 青岛 266580）

4（中石化经纬地质测控技术有限公司 青岛 266075）

随钻测井（Logging While Drilling，LWD）是大斜度井、水平井及定向井中实时、精准获取井下工程和地质参数的重要技术手段［1］。携带声、电、核传感器的随钻测井仪器在测量时受振动、钻进工况影响会出现仪器偏心或不贴壁、存在间隙的情况，使得测量状态与刻度时存在差异，导致结果受井眼环境影响而存在较大偏差，需要进行井眼校正才能保证测量效果。因此，准确计算仪器间隙和井眼直径（简称井径）是提高随钻测井测量精度的关键。

Yang等［2］提出利用超声回波时间间隔可以确定仪器与井壁的间隙，并计算井径大小。阮玉柱、胡凯利、Paske等［3-5］认为超声波测距方法测量井径速度快且信息量大，但超声间隙容易受到泥浆类型、岩屑、超声探头灵敏度及探头外侧泥饼的影响。Passey、Ellis、于华伟、张丽等［6-10］基于对密度测量响应规律及其影响因素的分析，认为密度测量值是地层密度和间隙填充泥浆密度的综合加权，其权重与间隙大小、泥浆的类型有关。Mickael、安旅行、Best等［11-13］通过分析近探测器视密度、地层密度、泥浆密度与间隙之间的关系，认为随钻方位密度测量可以用来确定间隙和井眼尺寸。陈翔鸿等［14］利用蒙特卡罗模拟研究不同井眼、间隙条件下随钻方位密度测量的响应规律，根据γ射线的窄束衰减模型推导得到间隙及井眼尺寸的计算公式。杨宁宁等［15］认为虽然窄束衰减模型可以较好地描述γ射线在常规密度地层（1.60~3.00 g·cm-3）中的衰减，但对低密度条件下γ射线的衰减无法准确表征。因此，考虑到间隙中低密度泥浆（通常小于1.60 g·cm-3）对γ衰减的影响，本文提出一种基于宽束γ衰减模型的间隙计算方法，从而进一步提高利用随钻方位密度测量计算间隙的精度及准确性。

首先通过分析密度测井中窄束和宽束γ射线衰减模型的适用范围，基于宽束γ射线衰减模型推导了间隙与密度测井响应的理论关系。然后参考已有的随钻方位密度测井仪器进行蒙特卡罗模拟，并根据实验测量数据对模拟结果进行基准检测。通过研究不同间隙、泥浆密度、地层密度等因素对探测器响应的影响，进一步得到间隙尺寸的计算公式。最后对实际井的测量数据进行处理，验证间隙计算方法的准确性。本研究所提出的间隙和井径计算方法可以为随钻超声井径测量做一种补充，为其他测井方法的井眼影响校正提供支撑。

1 随钻方位密度测井间隙计算方法

密度测井使用137Cs γ源向地层发射γ射线，通过测量探测器所接收到经地层康普顿散射后的γ射线强度确定地层密度。传统密度测井通常基于窄束γ射线的指数衰减模型来定量表征其响应规律，窄束γ射线是指不包含散射成分的射线束通过吸收物质后的γ射线。黄隆基等［16］认为密度测量所用的γ探测器基本只接收了地层中发生一次康普顿散射后的射线束，在较大源距且地层密度在1.60~3.00 g·cm-3范围内的响应近似符合窄束衰减规律。窄束衰减模型具有以下形式：

式中：N0为零源距时的探测器计数率；N为视源距为da的探测器计数率；μm为质量康普顿衰减系数；ρb为地层密度。

虽然窄束γ衰减模型可以描述大多数地层中γ射线到远探测器的衰减，但是随钻方位密度测量时，受间隙中低密度泥浆的影响，窄束衰减无法准确表征其衰减规律。尤其是近源距探测器会受到多次散射的影响更大，需要考虑累积效应的贡献。由于宽束衰减的密度应用范围可拓展至1.00~3.00 g·cm-3，因此，推导基于宽束衰减模型的间隙计算公式可以进一步提高其密度应用范围，其中没有间隙存在、单一测量介质时宽束衰减模型［15］为：

随钻方位密度测井仪器在旋转过程中，探测器正对的仪器外壁并不总是贴地层测量，使得井眼中仪器和井壁之间的间隙不断变化。一般利用近、远两个探测器所测计数率，分别用式（2）计算出ρfar、ρnear两个密度值，然后采用脊肋图方法近似补偿间隙的影响，从而近似得到地层密度ρb。其中ρfar和ρnear两个密度都是高密度地层和间隙中低密度泥浆共同作用的结果，而不是真实地层密度，并且ρnear由于源距短对间隙变化更加灵敏，更能反映间隙对密度响应的影响。

在间隙存在时，为了更加准确地表征γ射线在泥浆和地层中的联合作用，本文在式（2）单一介质衰减模型的基础上，加入间隙中泥浆的响应，从而将其扩展为双层介质衰减关系，具体为：

式中：ρm为泥浆密度；tm为间隙尺寸。此公式可以准确描述γ射线的作用过程，但存在ρb、ρm、tm三个未知参数，正常无法求解。但地层密度ρb可以经过脊肋图补偿确定，泥浆密度ρm可以通过现场钻井参数获取，式（3）中的未知参数仅剩间隙尺寸tm，因此，通过测量γ计数率N可得到间隙尺寸：

仪器在标准井中可以得到近探测器基于公式（2）的刻度关系：

将式（5）代入式（4）中，可得出间隙的计算公式为：

为了简化求解过程，借鉴杨宁宁［15］利用泰勒展开式的方法，将ln（ρb）、ln（ρnear）项用泰勒公式展开至第2项，可得：

进一步化简可得：

式中：a、b为拟合常数。

根据式（8），利用近探测器密度、地层真密度、泥浆密度三个参数即可确定井眼间隙尺寸的大小。

2 实验及蒙特卡罗数值模拟

2.1 仪器计算模型

本文根据某公司研制的随钻方位密度测井原理样机，利用蒙特卡罗模拟程序MCNP（Monte Carlo N-Particle Transport Code）构建了仪器、地层、井眼的三维数值计算模型［17-19］，如图1（a）所示。仪器主要包括137Cs源、近和远两个NaI γ探测器以及探测器之间的屏蔽体。其中，仪器直径为21.082 cm，屏蔽体材料为密度16.83 g·cm-3的钨镍铁。远探测器的源距为36.322 cm，近探测器的源距为16.002 cm，源和探测器外侧分别开准直孔。模拟时采用MCNP中的通用源，每次抽样1×108个粒子，同时使用DXTRAN球提高计算精度［20-22］，使每次模拟的统计误差小于1%。

2.2 模拟与实验结果基准检测

由于仪器实际结构非常复杂，在使用蒙特卡罗模拟程序建模时会进行一些简化，使得模拟结果与实际地层中仪器的测量结果会存在一定的偏差。因此，需根据仪器的实验数据对所建立的蒙特卡罗模拟计算模型进行基准检测，使其与实测结果相对应，提高计算结果的统计性和准确性［23］。

为了对比仪器实验测量与数值模拟的响应规律，在已知孔隙度的石灰岩标准刻度井中，完成了随钻方位密度测井原理样机的刻度实验工作，将仪器的实验数据与蒙特卡罗模拟数据进行对比，如图1（b）所示。

图1（b）中，空心数据点为实验刻度的测量结果，实心数据点为数值模拟的结果。其中，远、近探测器计数都随密度增大而减小。对比两种数据可以看出，蒙特卡罗模拟与实验测量的数据点基本重合，计数偏差在3%以内，证明蒙特卡罗模拟可以较好地反映实际测量的响应规律，并且可以得到仪器的响应关系来用于后续井眼影响研究。

3 模拟数据计算结果对比

3.1 间隙计算公式确定

根据第一部分推导的式（8）可知，仪器旋转测量过程中间隙的大小主要与三组变量有关，分别为地层密度与近探测器密度的平方差、地层密度与近密度的差值、地层密度与泥浆密度的差值。为了得到精确的间隙计算公式，分别研究间隙与这三组变量之间的关系，因此本文模拟了仪器在0~5.08 cm井眼间隙中分别充填1.00~1.60 g·cm-3泥浆的不同孔隙度饱含水砂岩、灰岩及白云岩地层条件下的近、远探测器响应关系。

利用地层密度与泥浆密度差值不变的模拟数据来研究间隙与另外两组变量之间的关系，如图2（a）、（b）所示。从图2可以看出，间隙和两组变量分别呈较好的线性正相关关系。这是因为对于相同地层，在地层密度与泥浆密度差值不变的条件下，间隙尺寸越大，近探测器测量受间隙泥浆影响越大，使得近探测器密度越小，导致地层密度与近探测器密度的平方差、地层密度与近探测器密度的差值都增大。

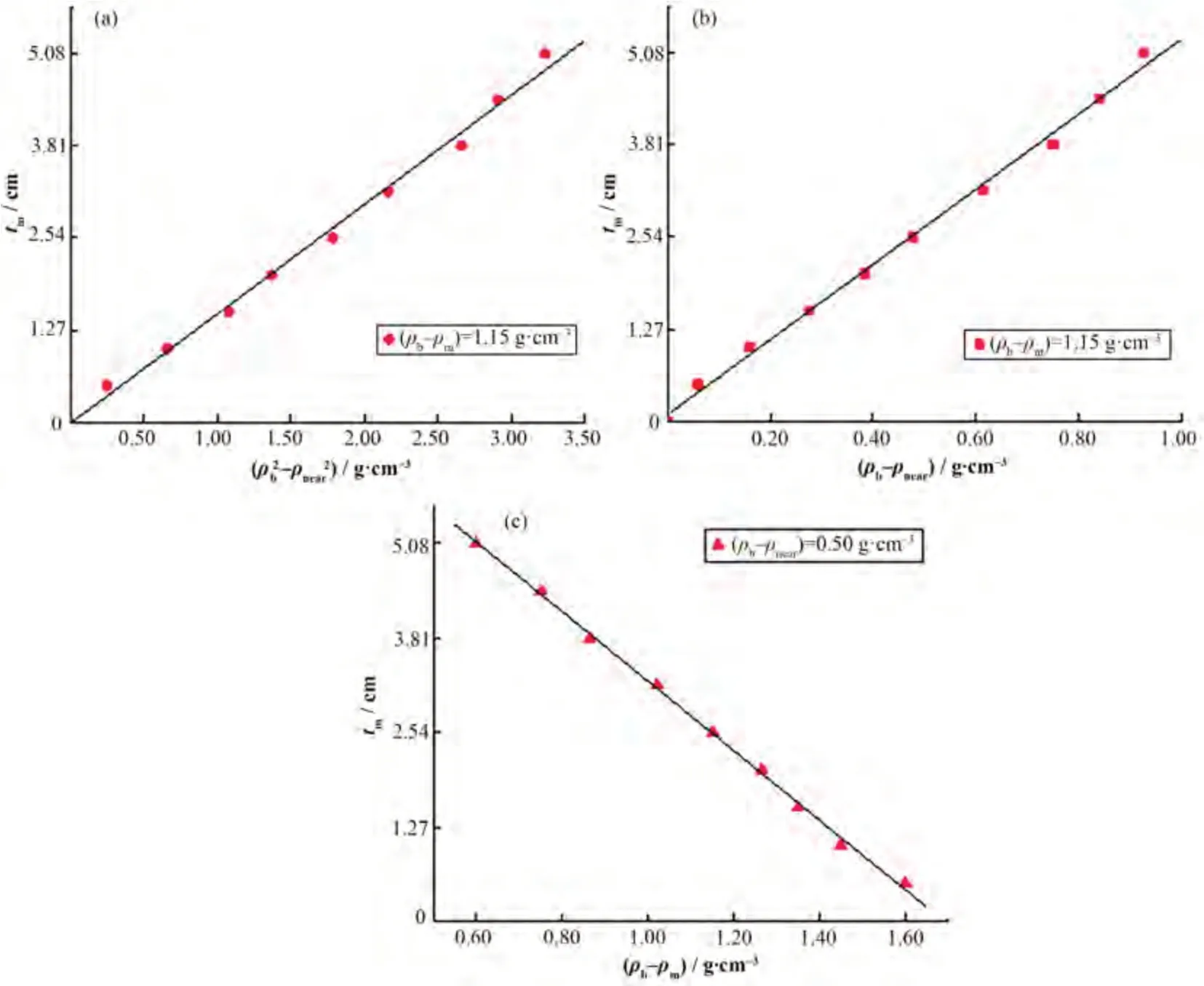
图2 间隙与三组变量的关系Fig.2 Relationship between the standoff and three sets of variables

另外，为了研究间隙和地层密度与泥浆密度差值的关系，选取地层密度与近探测器密度差值不变的模拟数据进行分析，结果如图2（c）所示。间隙与近探测器密度与泥浆密度的差值呈较好的线性负相关关系。对于同种地层，当地层密度与近探测器密度的差值不变时，间隙尺寸越大，泥浆对近探测器测量的贡献增多，泥浆密度增大才能保证近探测器密度不变，因此地层密度与泥浆密度差值会减小。

由以上分析可知，地层密度与泥浆密度差值不变时，间隙和地层密度与近探测器密度的平方差、地层密度与近密度的差值有较好的函数关系，通过拟合可得到相对精确的间隙计算公式。然而实际工程测量过程中，地层密度和泥浆密度时刻变化，因此需要建立不同地层密度与泥浆密度差值条件下的间隙计算公式，如图3所示。

图3中，x轴为（ρb2-ρnear2），y轴为（ρb-ρnear），z轴为间隙tm。地层密度与泥浆密度差值可分为0~0.67 g·cm-3、0.67~0.87 g·cm-3、0.87~1.10 g·cm-3、1.10~1.30 g·cm-3和大于1.30 g·cm-35个范围（对应图中的5条曲线）。每条曲线分别拟合间隙计算公式，实际工程应用时，确定地层密度和泥浆密度后选用相应范围内的间隙计算公式进行间隙的计算。

3.2 模拟数据计算方法验证

为了分析所提出计算方法的效果，将模拟数据中的地层密度、近探测器密度、泥浆密度分别带入拟合的计算公式中，同时代入陈翔鸿等［14］基于窄束γ衰减模型推导的间隙尺寸计算公式中分别计算间隙尺寸，将两种方法计算的间隙结果与模拟间隙理论值进行对比，如图4所示。

图4 模拟数据两种方法计算结果(a)和计算误差(b)的对比Fig.4 Comparison of calculation results (a) and calculation error (b) between two methods for simulation data

图4中，空心圆数据点代表模拟间隙的理论值，三角形、正方形数据点分别代表宽束、窄束方法间隙的计算结果。由图4可知，当间隙较小时，探测器响应受低密度间隙泥浆影响小，两种方法的间隙计算结果与间隙理论值均比较接近，误差较小。随着间隙增大，宽束方法的间隙计算误差保持在0.254 cm以内，但窄束方法计算误差变大。特别是在地层密度和泥浆密度都比较小的地层（如砂岩地层），窄束计算间隙误差相对较大。以上结果说明，受低密度间隙泥浆的影响，相比于窄束模型，本文所提出的基于宽束γ衰减模型的间隙计算公式更为准确，计算结果与间隙更为接近。

4 实测数据处理对比及分析

随钻方位密度测井仪在旋转钻进过程中测量并记录井周16个方位扇区的地层信息，每个扇区都可以利用密度信息计算间隙。为了验证所提出间隙计算方法在实际测量数据中的应用效果，对某井中实测数据加以处理，将计算得到的间隙尺寸与超声间隙对比。

根据某井中2 025.0 m处仪器16扇区的间隙计算值和仪器尺寸绘制井壁截面如图5所示。图5中仪器井周360°方向的地层被划分为16个扇区（0~15号，每个扇区的角度间隔为22.5°），顶、底部为0、8扇区，左、右部为4、12扇区［24］。

图5 某井2 025.0 m处井壁截面Fig.5 Cross-section of the borehole wall of a certain well at 2 025.0 m

利用CIFLog平台进行测井曲线绘制，将间隙计算结果与实测超声间隙进行对比。另外利用陈翔鸿等［14］提出的由不同方位仪器、井壁及间隙的几何关系所确定的井径计算方法计算井径，并与钻井后电缆井中的机械测量井径对比。由于井段过长无法全部进行显示，本文仅对井段2 000.0~2 060.0 m和2 075.0~2 115.0 m的数据加以截取，输出结果如图6所示。

图6 某井2 000.0~2 060.0 m (a)和2 075.0~2 115.0 m (b)测井曲线对比Fig.6 Comparison of logging curves of a certain well at 2 000.0~2 060.0 m (a) and 2 075.0~2 115.0 m (b)

图6中的输出结果共包括9道测井曲线。第1道为深度道，第2道中自然γ曲线的低值表示砂岩地层，高值代表泥岩地层，第3道为16扇区密度成像。第4、5道的曲线填充为顶、底及左、右超声间隙，曲线是顶、底及左、右密度计算间隙。第6道的虚线和实线分别对应密度计算井径和电缆机械测量井径，第7、8道分别对应0~7扇区、8~15扇区密度计算井径三维显示。第9道实线、虚线分别代表仪器、井眼的横截面，数值对应该深度处的360°井眼形状。

如图6（a）所示，第6道计算井径和电缆井径基本重合，第4道和第5道在间隙小于3.81 cm范围内计算的间隙与超声间隙一致性高，验证了本文所提出的间隙计算方法的准确性。仅在个别的井径偏大处，由于密度计算井径的适用范围受限，与电缆井径存在一些差别。

在分析这口井的数据时发现存在一些超声间隙测量异常的井段，如图6（b）所示。图中2 082.0~2 098.0 m井段的电缆井径曲线显示井眼有些扩径，超声井径测量的顶、底、左、右间隙值都较大，但一般应该是贴近井壁的扇区间隙值小、远离地层的扇区间隙值大，与工程实际存在一定偏差。而此段利用密度计算的4个方位的间隙有较好的规律，即顶部间隙大、其他方位间隙较小，说明仪器贴近井眼底部，且井径值也与电缆井径结果基本吻合。该井段的密度计算间隙比超声间隙结果更加准确，因此可以与超声间隙数据互为补充。

5 结语

1）本文基于宽束γ衰减模型推导出密度计算间隙的理论关系，利用蒙特卡罗模拟数据拟合确定了间隙的精确计算公式，对模拟数据和仪器实际测量数据进行处理，分析其应用效果。

2）模拟数据处理结果表明，与窄束方法相比，宽束方法计算的间隙值更为准确；实测数据处理结果中，间隙及井径的计算结果与超声间隙、电缆井径基本一致。在某些超声间隙测量异常的井段，计算的间隙更符合工程实际。

3）本文提出的宽束间隙计算方法，进一步提高了间隙的计算精度及应用范围，并且可对超声测量盲区进行有效补充。本研究对改善随钻测井中井眼环境影响的校正效果以及测量精度的提高具有重要意义。

作者贡献声明于华伟负责论文构思和公式推导；张倩文参与蒙特卡罗数值模拟建模，公式推导及应用和论文初稿撰写；王哲对初稿进行审核与编辑；罗琳对蒙特卡罗建模进行指导；刘睿参与研究问题讨论；于其蛟参与方法研究；杜海洋参与数据分析；韩春田提供数据资源。