基于KRUSTY带核实验的热管冷却反应堆瞬态分析程序验证
吴攀 欧阳泽宇 朱煜 单建强
(西安交通大学 核安全与运行实验室 西安 710049)
核工业界目前正在研发多种微型反应堆方案(简称“微堆”),微堆是指系统非常简单紧凑,能产生1~20 MW的热能直接供热或转换为电能利用的反应堆系统,具有模块化、可运输、自适应调节等核心关键特征,相较于传统反应堆具有微小便携、设计简单、可快速现场部署安装等优势,能够很好地解决国家的特种能源需求。在众多微堆类型中,热管冷却反应堆作为能量密度高、适应能力强的核电源系统,能在空间、深海探索等任务中发挥重要作用,因而越来越受到各国重视[1]。使用高温热管冷却堆芯的微型热管冷却反应堆具有高温运行、系统紧凑、固有安全性高的优点,便于模块化设计,可避免单点失效。此外,由于省却了一回路泵、阀门及管道系统,简化了系统布置并节省了系统体积,可避免传统商用反应堆可能发生的失水与失流事故[2]。高温热管通常采用锂、钠、钾等碱金属作为工质。高温热管的运行性能对高压堆的启动、稳态、瞬态和停堆都有显著的影响[3],相关研究表明,微型热管冷却反应堆在技术上较其他微堆概念更成熟,如美国洛斯阿莫斯国家实验室研发的MegaPower热管反应堆[4]预计于2025年进行原型验证,Kilopower热管空间堆[5]已于2018年完成了地面验证测试。因此,微型热管冷却反应堆成为了先进小型反应堆中最具应用前景的技术。
对于热管冷却反应堆,通过热管的热传递是堆芯裂变热输出的唯一方法[6]。为分析微型热管冷却反应堆在正常和非正常运行条件下的系统瞬态响应与安全特性,开展系统安全评估,需开发系统瞬态分析模型和程序[7]。现已有针对热管冷却双模式空间堆(HP-BSNR)开发的热工水力分析程序STHA_HPBSNR[8]、针对热管分段式热电模块转换器(Heat Pipes Segmented Thermoelectric Module Converters,HP-STMCs)空间堆开发了热工水力计算程序[9]、针对热管冷却空间反应堆电源系统(Scalable Alkali metal Thermal-To-Electric Conversion Integrated Reactor Space Power Systems,SAIRS)空间堆开发的系统瞬态分析程序TAPIRS[10]等,但由于国内外热管冷却反应堆相关实验开展较晚,这些程序仅对反应堆方案的稳态设计值进行了初步验算,未经过真实实验数据的验证。千瓦级热管反应堆实验(Kilowatt Reactor Using Stirling Technology,KRUSTY)是美国国家航空航天局(National Aeronautics and Space Administration,NASA)针对1~10 kWe级小型空间核反应堆电源Kilopower项目开展的实验项目,该实验是当前世界上唯一公开发表的基于斯特林技术的热管冷却反应堆带核实验,其结构设计如图1所示。目前,KRUSTY热管堆系统的28 h带核实验数据已经公开发布[11-12],为热管冷却反应堆系统分析程序的验证提供了十分有力的参考。
针对当前热管堆系统分析程序验证工作不足的问题,本文中介绍了自主研制的热管冷却反应堆系统瞬态分析程序TAPIRS-D的关键理论模型,并采用TAPIRS-D对KRUSTY热管堆系统的堆芯传热系统和热管传热系统进行了详细建模,模拟计算了带核实验中的多个运行工况,包括热管堆冷启动工况、负载变化瞬态工况、热管失效事故工况、反应性引入事故工况和热阱丧失事故工况,使用文献[11-12]中的实验数据评估了TAPIRS-D程序的堆芯功率瞬变模型、堆芯瞬态传热模型以及热管瞬态传热模型等的正确性。
1 TAPIRS-D程序关键模型介绍
TAPIRS-D程序是基于TAPIRS空间堆系统瞬态分析程序[10]进行模型改进优化二次开发的热管堆系统分析程序,可针对采用多种热电转换方式(包括静态和动态热电转化)、堆芯布置方式和废热排出方式(水冷或者辐射散热)的热管堆系统进行建模计算。TAPIRS-D程序的模型框架如图2所示,程序的分析模型主要包括堆芯功率瞬变模型、堆芯传热模型、热管传热模型、热电转换模型及废热排出模型,对于不同模块建立的微分方程组使用四阶标准龙格库塔方法进行联合求解。

图2 TAPIRS-D程序模型框架Fig.2 Model framework of TAPIRS-D program
由于KRUSTY热管冷却反应堆实验的模拟主要涉及的模块包括功率计算模块、堆芯传热模块以及热管传热模块,本节将简要介绍TAPIRS-D程序在这三个方面的基本理论模型。
反应堆的堆芯功率瞬变模型采用点堆中子动力学模型,使用同时适用于刚性显著情况与刚性不显著情况的高次端点浮动法[13]用于求解考虑了6组缓发中子的点堆中子动力学方程,堆芯的反应性反馈考虑燃料与热管等材料的温度反应性反馈。堆芯传热模型采用基于傅里叶定律和能量守恒定律的二维温度控制方程[14],使用显式差分方法可得到关于各控制体节点的温度微分方程组。热管传热模型则通过热管在凝固态启动阶段的自由分子流模型、“平面前锋”模型和正常工作阶段的热阻网格模型,全面模拟热管从启动到正常运行的全过程传热性能。
1.1 堆芯功率瞬变模型
1.1.1 点堆中子动力学模型
核反应堆的反应性快速变化可能会导致堆芯功率的快速变化,核反应堆裂变功率的控制是利用缓发中子的作用实现的[15]。由于微型堆的体积小,反应堆的中子动力学特性的空间效应并不明显,同时为了实现一维的瞬态系统分析程序的快速计算,TAPIRS-D采用考虑6组缓发中子的点堆中子动力学模型来计算反应堆功率大小及瞬态变化:
式中:N(t)为中子密度(功率水平),cm-3;ρ(t)为反应性,$;β为缓发中子总份额;λi为6组缓发中子先驱核的衰变常数,s-1;Ci为第i组缓发中子先驱核的浓度,cm-3;Λ为瞬发中子的平均寿命,s;βi为6组缓发中子份额。
1.1.2 反应性反馈模型
反应性反馈模型主要考虑堆芯燃料与基体材料的温度反应性反馈。在快堆运行期间,堆芯大小会发生变化,这主要是因为堆内温度变化引起构件的膨胀或移动,从而引起堆芯各部分中子吸收能力发生变化,考虑温度反应性反馈的堆芯总反应性计算式如下:
式中:αF为燃料温度反应性反馈系数,$·K-1为燃料平均温度,K;为燃料基准温度;αC为基体温度反应性反馈系数,$·K-1为基体平均温度,K为基体基准温度,K;ρext为外部引入的反应性,$。
1.1.3 控制鼓调节模型
热管反应堆常用的外部反应性控制方法是使用步进电机控制的控制鼓系统,控制鼓的主体是转轴可在0º~180º内旋转的圆柱形氧化铍(BeO)反射层转鼓,侧面一定扇面区域附有碳化硼(B4C)吸收体。当控制鼓朝外正向转动时,吸收体远离堆芯,堆芯中子更多地被反射,因此会向堆芯引入正反应性,反之则会引入负反应性。
控制鼓引入的外部反应性价值可以拟合为与控制鼓转角大小相关的多项式函数,图3所示为一典型控制鼓设计的反应性价值ρCD与转角θ间关系曲线图,其拟合关系式的形式如下:

图3 控制鼓反应性价值与转角之间的关系曲线Fig.3 Relationship curve between the reactivity value of control drum and the turning angle
1.2 堆芯传热模型
热管堆的堆芯结构相对复杂,大型热管堆的堆芯一般由一定比例的燃料与热管构成的燃料组件布置而成,堆芯放置在隔离层中,外层布置有BeO等中子反射材料组成的控制鼓。由于堆芯存在着径向导热,且实验中反射层与环境的热损失一般不可忽略,在失去废热排出系统的情况下,堆芯余热也是通过径向反射层导出堆芯的,因此首先建立了堆芯径向传热模型,将六边形堆芯区域等效为圆形,并将整个堆芯区域划分为热区、平均区、冷区、容器壁、反射层五个等效计算区域(图4),每个计算区域内可包含燃料棒、热管、基体、BeO棒等组件。计算区域的一维径向导热控制方程通过傅里叶定律和能量守恒定律得到:
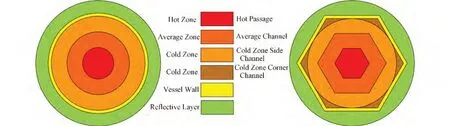
图4 堆芯径向分区示意Fig.4 Diagram of radial partitioning of the core
式中:V为计算区域体积,m3为计算区域平均温度,K;r为区域等效半径,m;S为内热源项,包括燃料产热、热管传热、对流散热功率等,W。
1.3 热管传热模型
反应堆堆芯的热量由热管导出,热管是一个比较复杂的系统,其工作全过程包含了许多传热模式,比如自由分子流换热模式、启动模式和正常换热模式等。高温碱金属热管运行在700~1 600 K的温度范围内,其内部压力小于0.1 MPa。热管的传热计算需要涵盖从冷态启动到正常运行的所有过程,根据工质转变温度Ttr,热管传热模型包括自凝固态启动阶段的自由分子流模型、“平面前锋”模型和正常工作阶段的热阻网格模型。对于高温热管启动早期的自由分子流阶段,管内以蒸发段工熔火质的熔化升温过程为主,蒸汽稀薄,绝热段、冷凝段工质仍处于凝固状态,因此该阶段可使用能量守恒方程描述:
式中:C(Te)为热管温度等于Te时的单位长度热容量,J·(m·K)-1;Te为蒸发段平均温度,K;Le为蒸发段长度,m;Qe为蒸发段热功率,Wt。
当工质温度上升至转变温度Ttr时,蒸发段蒸汽区进入局部连续流阶段,蒸汽向冷凝端扩散并在蒸发段外冷凝,使绝热段、冷凝段热管与工质温度上升。而由于热管壁较薄,轴向热传导的效率远不如蒸汽传热。在热管启动试验中发现,随着热量持续供给,蒸发段平均壁温Taw上升至某一中间值后将保持几乎不变,期间一条有陡峭温度落差的蒸汽界面自蒸发段(热区)向冷凝段(冷区)移动,当热区充满整个热管后Taw才继续开始上升,这一现象称为热管的“平面前锋”现象,如图5所示。

图5 标准热管“平面前锋”启动模型示意图Fig.5 Diagram of the standard heat pipe "flat front" startup model
Cao和Faghri据此提出了“平面前锋”分析解模型[16],由关于热区长度与温降的两个分析解组成。热区长度l是时间和热区平均温度Taw的函数,如下式所示:
式中:h*=2πrwh,Q(τ)=Q(τ)+h(Taw-Ta)(Le+La),ΔT=2(Taw-Ttr);l为热区长度;La为绝热段长度;Taw为热区平均壁温;Ta为热管初始温度;Q为输入热量;τ为加热时间;τi为热区到达冷凝段时的初始时间;hfg为工质汽化潜热;R为气体常数;Trf与Prf为工质饱和状态参考温度与压力;rv为蒸汽区半径;μv为蒸汽动力黏度。
正常工作时的热管常使用Zuo和Faghri提出的热阻网格模型[17],该模型将热管的每个传热过程视作一维热阻导热,而忽略了蒸汽的热容和热阻,如图6所示。一维热阻模型存在较多的局限性,比如未考虑可能遇到的传热极限问题、忽略了绝热段径向导热且无法考虑实际中绝热段的壁面可能存在的热损失、温度场不够精细等。为了改进传统热阻网络模型对于热管堆系统瞬态分析的诸多不适用性,本文基于热阻网络模型的分析思想建立了连续流阶段的二维传热网格模型。模型仍然将热管壁、液环与吸液芯内的导热过程视作固体接触导热,但考虑了运行中可能发生的传热极限问题,将热管吸液芯与蒸汽区间视作热流边界对蒸汽的换热量单独求解,并对于热管结构作出了更精细的控制体划分,如图6所示。模型中的各节点温度的控制方程为二维导热全隐差分方程,易于使用交替隐式差分(Alternating-direction Implicit,ADI)算法进行求解[14]。
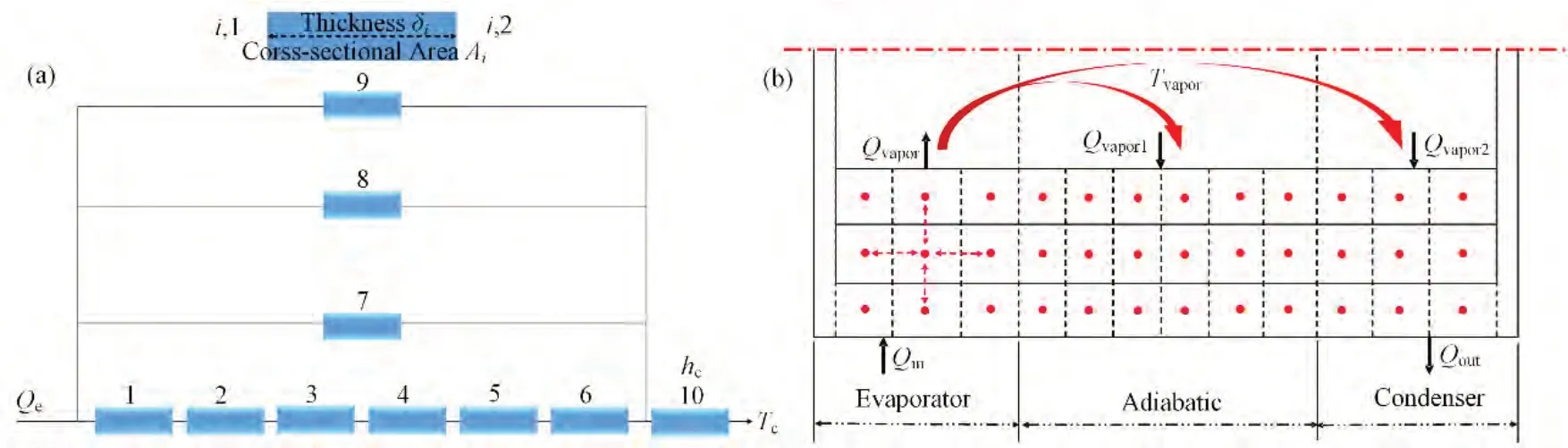
图6 SBL-30热管正常运行时的传热模型 (a) 热管一维热阻网络模型,(b) 改进的二维热阻网络模型Fig.6 Heat transfer model of heat pipe in normal operation (a) Heat pipe one-dimensional thermal resistance network model,(b) Improved two-dimensional thermal resistance network model
2 KRUSTY系统建模与整体验证
2.1 建模研究与稳态工况
基于斯特林技术的千瓦级热管堆实验是目前国内外唯一完成的带核热管堆全系统实验,该实验开展了28 h,包括了热管堆启动、稳态运行、瞬态运行与多种事故工况。KRUSTY热管堆是一个小型的实验快中子堆,设计的稳态热功率为4 kW,输出电功率1 kWe;使用三个全固态的U-8Mo环形燃料元件堆叠形成堆芯,中心为B4C控制棒;圆柱燃料侧面挖槽嵌入8根钠热管,呈对称式布置,热管将热量自堆芯传递给热电转换装置,KRUSTY反应堆的布置如图7所示。因为考虑到成本限制与斯特林机可能存在制造差异而带来误差,实验仅安装了两个ASC-E2型小型斯特林机,另外使用了6个氮气冷却装置来模拟斯特林机,气冷模拟器的功率跟斯特林机保持一致。

图7 KRUSTY堆芯布置图 (a) 堆芯横截面图,(b) 堆芯实物图Fig.7 Diagram of KRUSTY core layout (a) Cross-sectional view of reactor, (b) Physical view of reactor
KRUSTY反应堆采用的是自通动脉钠热管(Self-venting arterial heat pipe),该热管插入堆芯后必须竖直放置,启动前热管蒸发段底部聚积有钠液池,受到加热后产生钠蒸气,扩散至冷凝段传热,钠蒸气液化后主要自内壁面的动脉通道由重力作用向下回流至液池形成循环,吸液芯网构成的液体动脉通道仅附着一部分内壁面,如图8所示[18]。尽管结构与标准高温热管结构有所区别,但瞬态运行的机理仍然是一致的,在建模时可以按照体积等效几何尺寸转化为标准的壁面-液环-吸液芯三层模型。

图8 自通动脉钠热管结构图Fig.8 Structure diagram of self-passed arterial sodium heat pipe
为验证TAPIRS-D系统瞬态分析程序计算的准确性,对该热管堆进行了较完整的建模,对多实验工况进行了模拟计算,并与实验数据进行了对比[8]。系统程序中堆芯功率瞬变模型使用文献中根据MCNP计算得到的点堆中子学参数[19],如表1所示,并考虑了燃料、反射层和热管温度负反馈效应,总的温度负反馈系数为-0.2 $·K-1,该反应堆没有控制鼓系统,因此省略控制鼓模型。

表1 SAIRS-C热管堆的关键参数Table 1 SAIRS-C heat pipe reactor key parameters
在堆芯建模时可将堆芯简化为控制棒-堆芯-热管的三层径向结构,堆芯结构与程序建模示意图如图9所示。将堆芯径向划分为两层控制棒与三层燃料,燃料最外层(第5层)与热管壁间设置有热流边界条件,热管壁温度为热管蒸发段壁面节点的温度,可根据傅里叶导热公式计算热流量。由于堆芯与反射层间存在真空隔热层,堆芯向反射层的散热较小,将堆芯对外热损失计入第5层的内热源项。
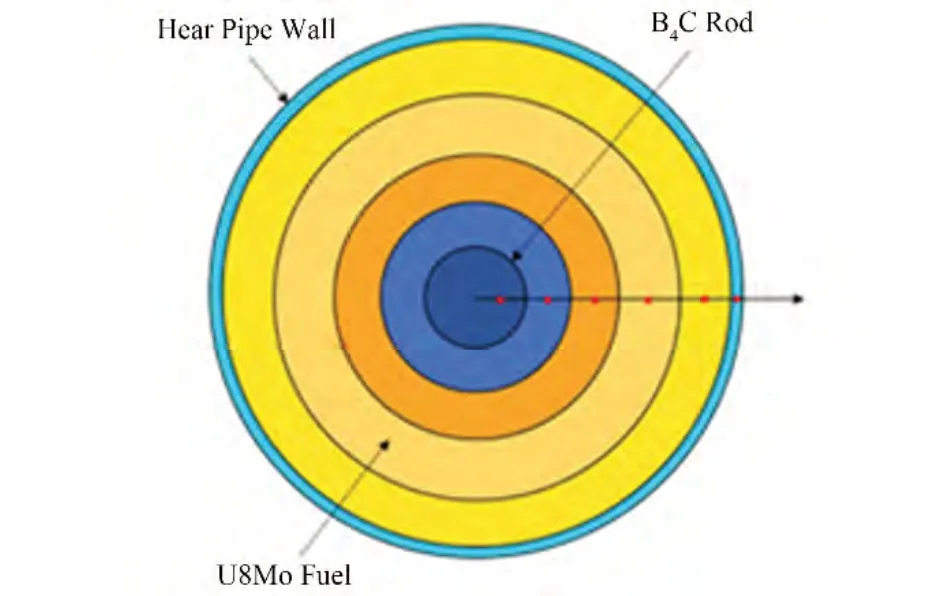
图9 KRUSTY堆芯的建模示意图Fig.9 Diagram of KRUSTY core modeling
对热管建模时,热管几何结构参数由文献中得到,蒸发段边界条件为堆芯向热管的传递热量,冷凝段边界条件为已知换热系数与斯特林机热端温度。由于缺乏斯特林机与水冷模拟器的具体参数,根据文献中测量的斯特林机热端温度数据作为热管的边界条件输入程序。
本文开发的布雷顿热电转换模型是开式布雷顿系统,压缩机入口与汽轮机出口并不相连通,未形成闭合管道回路,由于缺乏开式布雷顿系统相应实验数据,为验证该模型,选择了Sandia实验室的SBL-30闭式布雷顿系统的运行实验进行建模计算[19],将闭式布雷顿系统中部分参数作为边界条件输入,近似处理为开式布雷顿系统。
整个KRUSTY反应堆系统的主要参数如表2所示。

表2 KRUSTY反应堆部分参数Table 2 KRUSTY reactor main parameters
对KRUSTY的建模完成后,首先选择了28 h实验中7.5~8 h时的稳态运行工况,给定各热管冷凝段的边界平均热流量进行了稳态计算。计算结果与实验数据对比如表3所示,程序计算得到的稳态堆芯裂变功率和燃料表面平均温度均与实验数据符合良好,误差小于1%,证明了TAPIRS-D程序对于热管堆整体稳态传热过程和堆芯功率反馈模拟的准确性。

表3 稳态计算结果验证Table 3 Steady state result comparison
2.2 热管堆冷启动工况
KRUSTY实验的0~1 h时进行了反应堆冷启动实验,初始时反应堆与环境达到热平衡,斯特林机处于关闭状态,在T=0.37 h时,通过引入反应性使堆芯功率由0开始逐渐提升至最高3.7 kW并稳定在3.1 kW,堆芯与热管壁温由初始环境温度300 K上升至800 K左右,在T=0.92 h时热管成功启动进入稳定工作状态。
文献[12]给出了一个靠近堆芯上部的热管壁测温点(测点1)和一个热管绝热段中部测温点处8根热管的平均壁温值(测点2)。根据热管堆启动初始状态与功率变化数据,程序计算的热管测点处壁温结果与实验数据的对比如图10所示。可以看到,在0.4~0.6 h期间,测点1处的温度开始逐渐上升,这表明反应堆的热量已经逐渐传递到与反应堆相接触的热管蒸发段,在0.6 h左右蒸发段温度超过400 ℃,钠蒸气开始在热管内运动,在0.67 h左右,测点2的温度开始出现了急剧增加,表明此时钠蒸气运动到了热管绝热段的中部。从图10可以看出,计算的测点温度值与实验值的变化趋势基本一致,表明TAPIRS-D程序的模型能够合理地反映出热管启动时的壁温变化与前文提出的“平面前锋”的推进情况。
热管堆冷启动计算过程中热管壁温的偏差主要可能来源于:1)程序中堆芯与热管材料的热物性拟合函数与实验中材料实际值存在一定差异;2)KRUSTY使用的热管是垂直放置的“自通动脉”式热管,底部有钠液池,其工质回流受到重力作用,内部结构也不同于传统高温热管,尽管启动机理同高温热管类似,但程序使用的热管启动模型计算会存在一定偏差。
2.3 负载变化瞬态工况
实验中T=8.0 h时将气冷模拟器的流量下降一半,使每个模拟器的冷却功率由290 W降低至210 W左右,以模拟热管堆负载降低瞬态。当初始时刻降低热管冷却功率时,热管与堆芯由于热量累计导致温度上升,引起温度负反馈效应,使堆芯功率下降而遏制温度上升,只造成了很小的温度波动,最终震荡衰减至达到一个新的稳态,堆芯功率由2.75 kW下降至2.05 kW左右。TAPIRS-D程序通过改变热管边界条件计算了该瞬态工况的堆芯功率与系统温度响应,计算结果与实验数据对比如图11所示。

图11 负载降低工况验证结果 (a) 堆芯裂变功率瞬态变化,(b) 燃料组件温度瞬态变化Fig.11 Verification results of load reduction condition (a) Core fission power transients, (b) Fuel assembly temperature transients
在T=9 h时,气冷模拟器的冷却功率调回正常值,反应堆重新进入稳态工况,裂变功率回到2.75 kW。随后,当T=10.02 h时,气冷模拟器的流量上升一倍,使每个模拟器的冷却功率由295 W提高至510 W左右,以模拟负载增大瞬态。当提高热管冷却功率时,热管与堆芯的温度下降使堆芯反应性上升,导致堆芯功率上升,产生堆芯功率与温度的震荡并逐渐衰减至达到一个新的稳态,堆芯功率由2.75 kW上升至2.05 kW左右。程序计算了该瞬态工况的堆芯功率与系统温度响应,与实验数据对比如图12所示。

图12 负载增大工况验证结果 (a) 堆芯裂变功率瞬态变化,(b) 燃料组件温度瞬态变化Fig.12 Validation results for load increase conditions (a) Core fission power transients, (b) Fuel assembly temperature transients
由于热管堆的负反馈效应,在负载发生降低或者增大工况时堆芯功率都能够收敛至稳态,从上述分析可以看到,新的稳态下TAPIRS-D程序预测得到的稳态功率与温度水平与实验数据符合较好,计算结果与实验数据震荡的周期也比较一致,但在功率和温度的振幅方面误差较大,这可能是因为KRUSTY建模信息不够完整导致的。总的来说,程序预测的系统参数响应趋势与实验数据一致,温度的最大误差小于1%,功率的最大误差小于10%,计算的功率与温度峰值与实验数据峰值时间对应基本一致,最终预测应达到的稳态位置也与实验数据符合良好。
2.4 热管失效事故工况
根据热管在燃料芯块的角度位置将燃料划分为8个区域,实验中T=12.0 h时,堆芯0º方向的热管所连接的模拟器氮气流量被切断,以模拟单点故障导致的热管失效事故,该处热管的散热功率由290 W降低至120 W。随后在T=12.5 h时,增加了0º位置以外的模拟器和斯特林机的功率,平均散热功率增加约50 W,模拟了故障后需要增加负载使总发电功率回到正常水平的操作。实验测量了与0º区域相邻的45º区域和相对的180º区域的燃料外层温度和堆芯裂变功率的响应情况,程序计算了这一事故工况,结果与实验数据对比如图13所示。
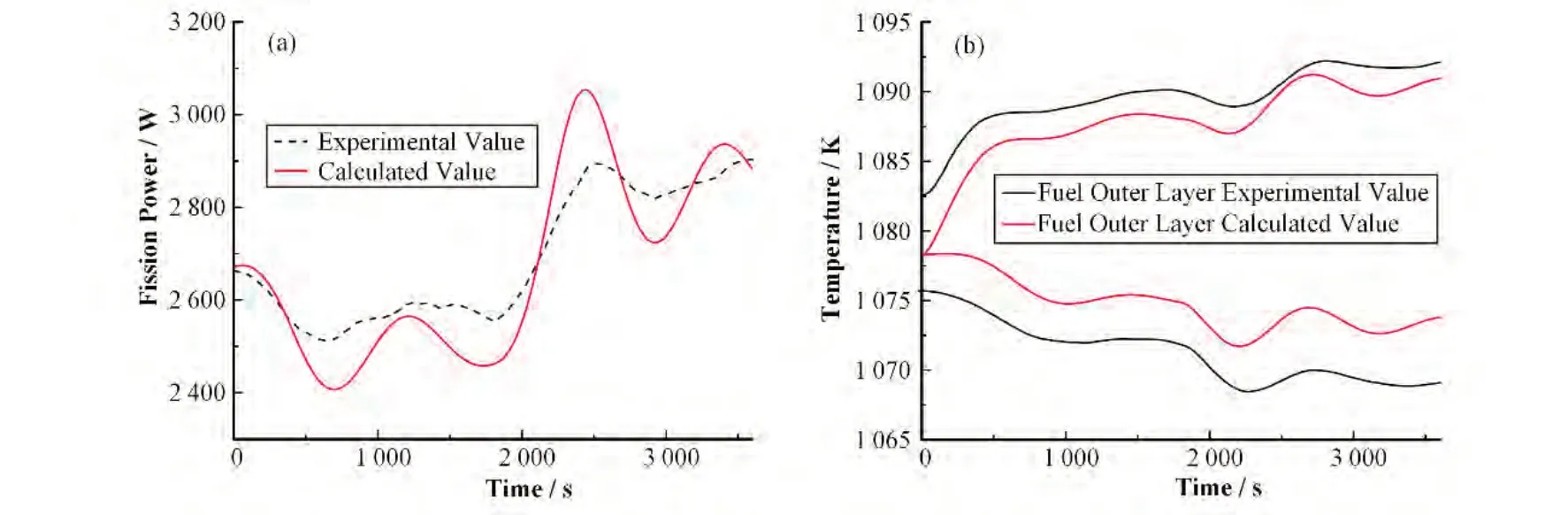
图13 热管失效事故工况验证结果 (a) 堆芯裂变功率瞬态变化,(b) 燃料组件温度瞬态变化Fig.13 Validate results of heat pipe failure accident (a) Core fission power transients, (b) Fuel assembly temperature transients
程序计算的功率与温度响应与实验数据符合较好,瞬态变化趋势一致,温度的最大误差小于1%,功率的最大误差小于4%。温度计算的误差主要来源于初始取值与实验值的偏差,这是因为实验中堆芯功率存在周向不均匀分布,导致燃料芯块周向温度也存在不均匀分布的原因。但由于文献中缺乏三维功率分布数据,程序无法模拟这种不均匀分布情况,故计算时燃料的初始稳态温度取两位置测量值的平均值。当0º位置热管散热功率降低时,该处燃料的多余热量只能从其他位置的热管排出,使相邻的45º区域局部温度上升;但同时堆芯热量导出受阻导致了堆芯平均温度升高,燃料的温度反馈引入了负反应性使堆芯整体功率降低。而由于0º区域向相对的180º区域传递热量很小,故180º区域燃料的局部温度反而因堆芯功率的下降而降低,使堆芯周向温度分布变得更加不均匀。在T=12.5 h时,散热功率上升导致堆芯温度下降,引起了堆芯功率的上升,会使热管失效区域的局部温度继续上升。程序计算结果很好地表现出了上述温度分布不均匀性的现象。
2.5 反应性引入事故工况
在实验的T=15.0~16.0 h,反应堆调回至稳态功率水平,T=16.0~16.05 h时,通过控制堆芯外围径向反射层套筒向下移动0.5 mm,引入了5.5 $的负反应性。使用程序从稳态开始计算了该负反应性引入事故工况,结果如图14所示。
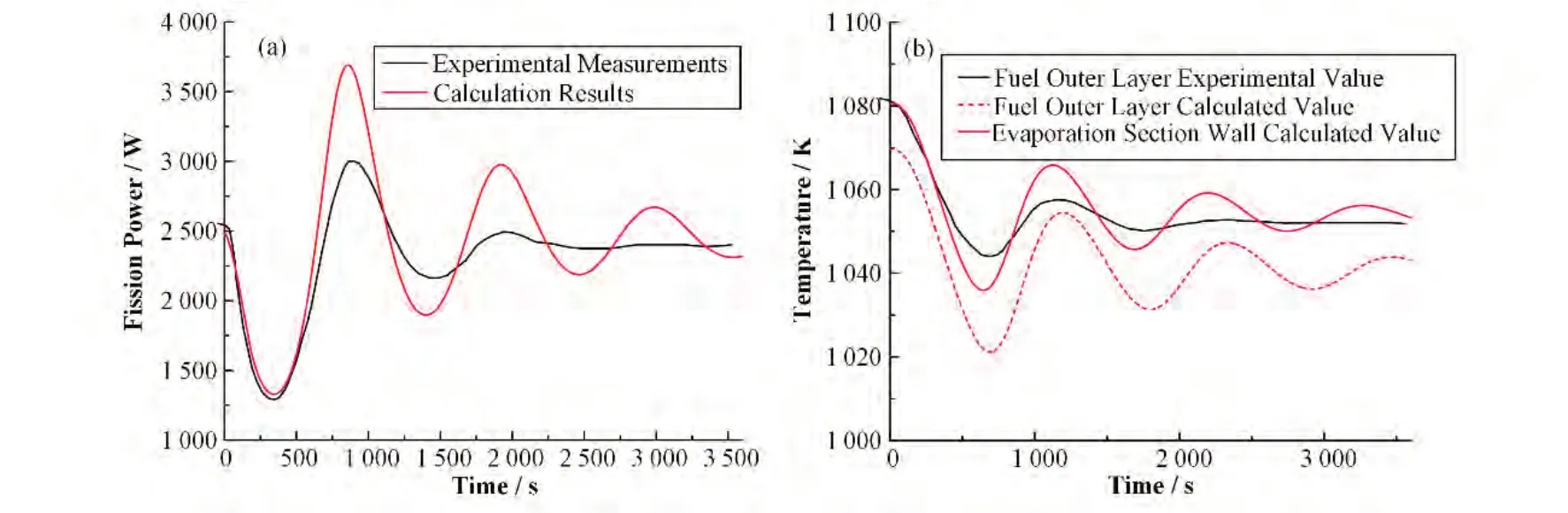
图14 负反应性引入事故下斯特林热电转换的参数响应 (a) 堆芯裂变功率瞬态变化,(b) 燃料组件温度瞬态变化Fig.14 Parametric response of Stirling thermoelectric conversion under negative reactivity introduction accident(a) Core fission power transients, (b) Fuel assembly temperature transients
反应堆在引入负反应性后功率迅速下降导致温度下降,温度的负反馈效应迅速补偿了该负反应性使功率回升,经一定震荡后功率回到正常稳态水平,计算表明最终燃料平均温度下降了27.7 K,这与实验测量的前后温差29 K基本一致。
在实验的T=18.0~19.0 h,反应堆的反射层套筒从正常位置下方1.0 mm开始提升了1.5 mm,总共引入了大约17.8 $的正反应性,此阶段堆芯功率最大上升至5 kW左右,是整个KRUSTY热管堆实验中的峰值功率。正反应性引入事故工况的计算结果如图15所示,反应堆在引入正反应性后功率迅速上升,温度升高引起负反应性补偿又使功率回降,震荡衰减后达到新的稳态。

图15 正反应性引入工况验证结果 (a) 堆芯裂变功率瞬态变化,(b) 燃料组件温度瞬态变化Fig.15 Validate results of positive reactivity introduction(a) Core fission power transients, (b) Fuel assembly temperature transients
程序预测的功率和温度响应与实验数据的趋势基本保持了一致,尽管变化振幅和功率峰值谷值仍然较实验数据有一定偏离,但对于燃料温度的预测偏差较小,温度的最大误差小于2%,最大功率计算误差约为16%,功率平均计算误差小于10%。
本文在进行实验验证时,无法准确获得燃料或包壳的真实物性,而是通过实验文献对燃料或包壳的描述,预估出物性参数用于瞬态计算。因此,在瞬态计算过程中,燃料温度变化的幅度会与真实情况有差异,同时,燃料温度变化通过多普勒效应,进一步影响反应堆的功率变化,从而导致反应堆的堆芯功率和燃料温度的震荡幅度与实际测量存在一定偏差。
2.6 热阱丧失事故工况
实验T=20 h时,将斯特林机空转,模拟器气体流量减至最低,使全部热管仅靠环境中空气的对流进行被动散热,模拟了反应堆的热阱部分丧失事故,该工况下热管冷凝端的平均冷却功率由270 W下降至约130 W,程序模拟了这一事故工况,计算结果与实验数据对比如图16所示。热阱冷却功率的下降导致热管与堆芯温度快速上升,燃料的温度负反馈效应又使堆芯功率降低,遏制了堆芯温度的上升并最终达到与降低后的冷却功率相匹配的新稳态。计算的燃料外层温度在2 h前后上升了约4 ℃,其中,2 ℃是由于实验的温度漂移现象导致。此外,由于低功率下的堆芯径向温度分布较高功率下更加均匀,故燃料外层温度较内层上升更快,这与实验测量结果基本一致,温度的最大计算误差小于1%,平均功率误差小于5%。
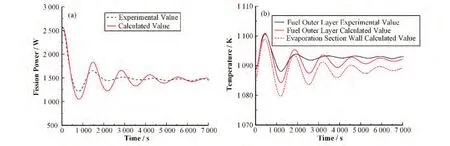
图16 热阱丧失事故工况结果验证结果 (a) 堆芯裂变功率瞬态变化,(b) 燃料组件温度瞬态变化Fig.16 Validation results for loss of heat sink accident (a) Core fission power transients, (b) Fuel assembly temperature transients
3 结语
本文使用自主研发的热管堆瞬态分析程序TAPIRS-D对KRUSTY热管堆实验系统进行了完整的建模,并模拟了KRUSTY实验开展的热管堆冷启动、运行稳态、负载变化、热管失效事故、反应性引入事故与热阱丧失事故工况实验,得到了各工况下堆芯功率、温度与反应性的瞬态响应,并与实际测量数据进行了对比。结果表明:程序预测的系统响应与实验数据符合较好,计算结果与实验数据对比符合较好,各工况下程序计算的燃料温度的最大相对误差小于2%,整体功率的平均相对误差小于10%,预测的堆芯功率与温度瞬态响应与实验数据趋势符合一致。验证结果表明,自主研发的TAPIRS-D在堆芯功率瞬变模型、堆芯传热模型与热管传热模型方面的准确性与可靠性,可为热管堆热工与安全分析提供有效参考。
作者贡献声明吴攀负责程序研发、数据收集及系统建模;欧阳泽宇负责程序研发、数据收集及系统建模;朱煜负责系统建模与验证;单建强提供技术材料支持并指导。

