铅铋流量计标定装置开式换向器运行特性模拟及不确定度分析

朱喻成 范旭凯 彭天骥,4 范德亮,4 唐延泽,4 田旺盛,4

1（中国科学院近代物理研究所 兰州 730030）

2（先进能源科学与技术广东省实验室 惠州 516029）

3（惠州离子科学研究中心 惠州 516000）

4（中国科学院大学 北京 100049）

铅基快堆是6种第四代反应堆之一，具有安全性好、经济性佳、体积小、核废物少等优点，具有广阔的应用前景。中国科学院近代物理研究所正在建设的“十二五”国家重大科技基础设施加速器驱动嬗变研究装置（China initiative Accelerator Driven System，CiADS）［1］采用铅铋快堆作为乏燃料的焚烧器。作为使用新型冷却剂的先进反应堆，铅铋快堆中液态铅铋流量测量与堆芯流量分配［2］是其热工水力研究、反应堆运行监测中的关键问题。在铅铋快堆的实验研究和运行中，为了实现流量的准确测量，需要对高稳定性的流量计进行高精度的标定。由于国内铅铋流量计的研制起步较晚，目前国内尚无高精度且产品成熟的铅铋流量计标定装置用来服务于流量计的研制和检定。

流量计的标定方法主要分为静态法、动态法和标准表法［3］。迄今为止，铅铋流量计的标定主要采用动态容积法和标准表法。中国科学院核能安全技术研究所的卢洋［4-5］使用标准表法标定了自行研制的铅铋电磁流量计，但其使用的标准表未经过铅铋实流标定，精度较低。美国阿拉莫斯国家实验室（Los Alamos National Laboratory，LANL）的Tcharnotskaia［6］、欧洲核能署（European Nuclear Energy Agency，ENEA）的Agostini［7］、日本原子能机构（Japan Atomic Energy Agency，JAEA）的Saito等［8］以及西安交通大学的Liu等［9］均使用动态容积法对铅铋流量计进行了标定，但动态法在动态称量时会引入动态误差，同时由于量具精度一般低于衡具，所以此类标定方法的精度较差。鉴于这种情况，中国科学院近代物理研究所正在开展基于静态质量法的铅铋流量计高精度标定装置的研制工作。

在静态质量法标定装置中，换向器的不确定度分量是流量计标定装置不确定度的主要组成部分［10］。换向器按结构可分为开式换向器与闭式换向器，闭式换向器经验证在铅铋介质下切换时会产生严重的水锤效应影响上游流量稳定性进而影响标定精度［11］，由此标定装置考虑使用开式换向器。

开式换向器一般由气缸或者电机驱动。电机驱动换向器正反输出一致性较好但其换向时间较长，由于换向器喷嘴出口处流体速度非完全均匀［12］，换向时间的增加会增大换向器引入的系统误差。气缸驱动换向器能够在较短时间内完成换向过程，但气缸一般存在正反输出力矩不一致的问题，所以有必要对气缸驱动开式换向器引入的标定相对系统误差以及其不确定度进行先验分析。

德国联邦物理技术研究院（Physikalisch-Technische Bundesanstalt，PTB）的Engel等［12］利用计算流体动力学（Computational Fluid Dynamics，CFD）及实验对换向器造成的系统误差进行了分析，认为换向器对标定造成的系统误差主要来源于换向器上游喷嘴处的流体速度的不均匀以及换向器挡板正反行程的不对称。

浙江省计量科学研究院的马龙博等［13］建立了换向器不同计时时刻下引入的标定相对系统误差的数学模型，并进行了实验验证，分析得到使用行程中点作为计时时刻时换向器引入的相对系统误差最小，但其在实验验证过程中认为在使用行程中点作为计时时刻时引入的标定相对系统误差为0，忽略了换向器换向行程速度不均匀引入的系统误差。

在实际的标定实验中无法确定换向器的标定相对系统误差而只能得到其不确定度，通过CFD可以同时得到其B类不确定度及标定相对系统误差。为了确定铅铋流量计标定装置中换向器引入的系统误差，本文基于CFD方法提出了一种用于开式换向器计算的双向耦合计算模型，实现了对气缸驱动开式换向器相对B类不确定度的先验分析并得到了换向器造成的标定相对系统误差。

1 基于开式换向器的铅铋流量计标定装置设计

中国科学院近代物理研究所设计的基于静态质量法的铅铋流量计标定装置的流程图见图1。在标定装置运行过程中，泵将铅铋由缓冲罐泵入稳压罐中使其保持稳定的压头，铅铋液体先后流经调节阀、被检流量计、换向器，流入缓冲罐或称重罐中。在标定开始前，换向器挡板位于左侧，铅铋经换向器流入到缓冲罐中：当标定开始时，换向器挡板向右动作将铅铋引入称重罐中；当标定结束时，换向器挡板向左动作将铅铋引回缓冲罐中。

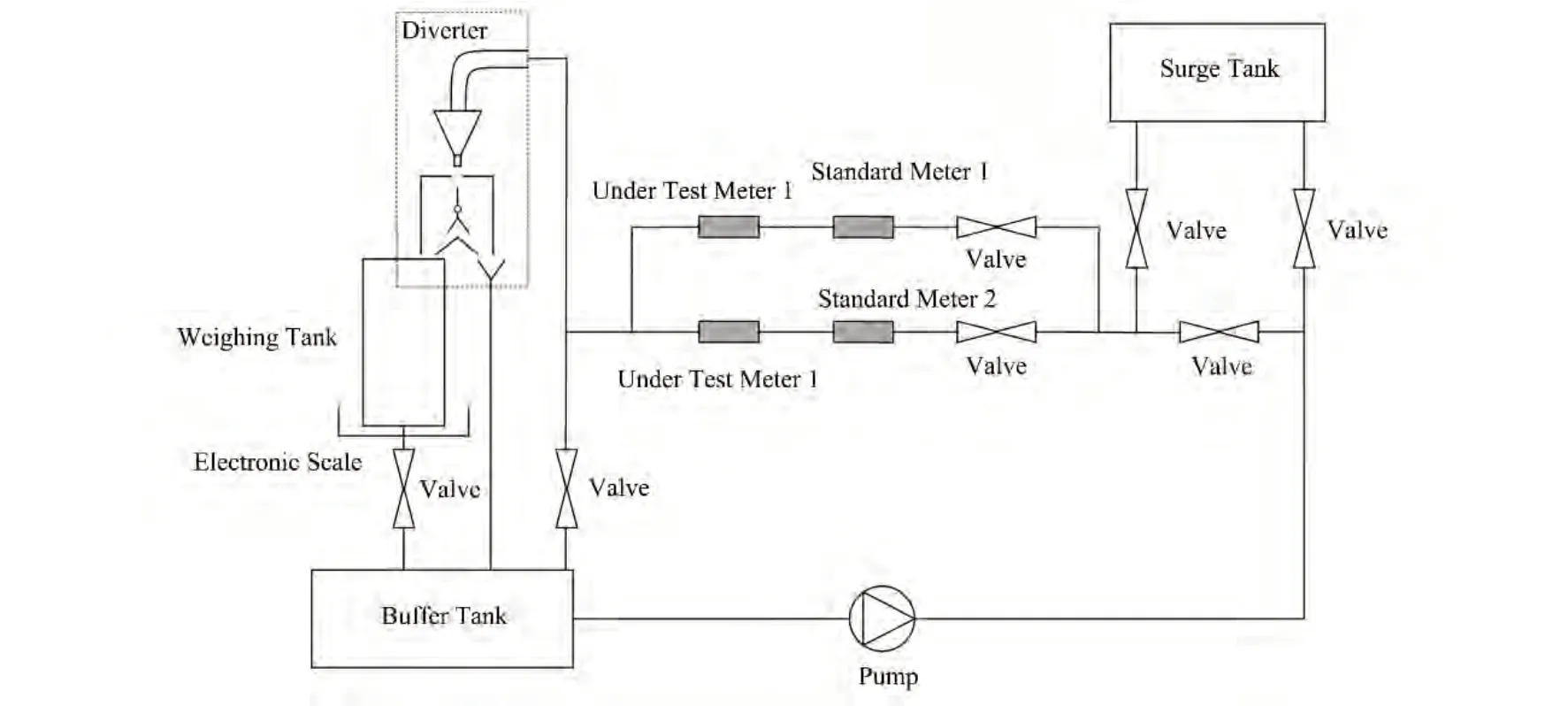
图1 铅铋流量计标定装置流程图Fig.1 Flowchart of the Lead-bismuth flow calibration facilities

按照设计，标定装置可以通过静态质量法实现高精度标定，也可以通过标准表法进行精度传递，其中静态质量法的设计不确定度为0.33%。装置适用的流量计量程范围为5~209 kg·s-1。考虑到装置承重以及运行成本，目前标定装置在最大流量下的称量时间为30 s。

2 换向器分析模型

2.1 设备分析模型

2.1.1 喷嘴与换向器结构

铅铋流量计标定装置的换向器参考水介质流量计标定装置的换向器方案进行设计［14］。换向器主要由喷嘴、挡板、导流器以及驱动装置构成，其结构示意图见图1。在装置运行时，铅铋经喷嘴流入换向器内，经挡板与导流器引入称重罐或缓冲罐。

2.1.2 喷嘴分析模型

受限于喷嘴上游管道的空间布置分布，实际喷嘴出口速度分布并非均匀分布，喷嘴出口的速度分布会对换向器换向时流入称重罐的流量产生影响，进而影响换向器在换向过程中造成的标定误差。为了得到喷嘴出口的速度分布，建立了如图2所示简化后的喷嘴出口及上游管道模型，其中上游管道直径设定为125 mm，喷嘴出口按《GB/T 17612-1998封闭管道中液体流量的测量 称重法》［15］对流量出口的要求设定为宽13 mm、长156 mm。

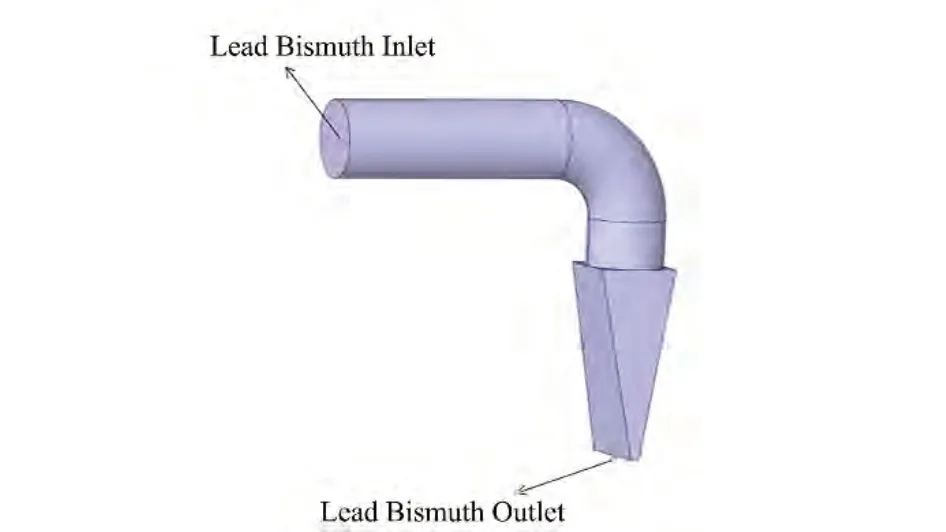
图2 喷嘴出口及上游管道简化模型Fig.2 Simplified model of nozzle outlet and upstream pipeline

由于喷嘴流动为稳态过程且不涉及多相流动，为了减少整体计算量，可将其与换向器解耦进行分析。上游管道入口设定为速度边界，喷嘴出口设定为压力边界。本文中计算时均使用600 K时的铅铋物性［16］，其物性如表1。

表1 600 K时的铅铋物性Table 1 LBE physical properties at 600 K

2.1.3 换向器分析模型

在标定开始时，气缸驱动换向器挡板绕转轴顺时针旋转，将铅铋从装置引入称重罐，挡板总行程为12°。为了防止铅铋被挡板下摆转向冲击换向器内壁出现挂壁造成误差，本文使用换向器挡板尖端分割喷嘴出口面积结合出口处流量分布函数进行流量统计，同时为了减小计算量，换向器分水器外的隔仓不参与建模。简化后的模型如图3所示，喷嘴出口（绿色面）设定为速度入口，顶部与底部（红色面）设定为压力入口。

图3 换向器简化模型（彩图见网络版）Fig.3 Simplified model of diverter (color online)

换向器分析模型计算网格划分示意图见图4，本文使用滑移网格方法来模拟换向器换向即挡板旋转过程。装置设计流量标定范围为5~209 kg·s-1，最小流量工况下喷嘴出口雷诺数约为35 000，选用SSTk-ω湍流模型进行计算。计算选用欧拉多相流模型，该模型建立了一套包含n个动量方程及连续方程的模型来求解，各相在交界处进行质量、能量以及动量传递［17］，相较于其他常见的多相流模型，欧拉模型能够更准确地模拟在换向器中铅铋喷入气相这一物理过程。

图4 换向器模型计算网格Fig.4 Calculation grid of diverter model

2.1.4 气缸动力学模型

气缸主要由活塞杆、活塞、缸筒及缓冲垫构成，工作时活塞受压带动活塞杆驱动机构作直线往复运动。气缸理论输出力与使用压力与作用面积有关，与行程无关［18］。对于单杆双作用气缸，其气缸理论推力（活塞杆伸出）为：

理论输出拉力（活塞杆返回）：

式中：Fo为气缸输出力；D为气缸直径；dp为活塞杆直径；p为气缸工作压力。

活塞杆作为气缸中最重要的受力件，其强度对气缸的可靠性及寿命至关重要。为了保证活塞杆的强度，活塞杆的直径设定为气缸直径的2/5~1/2，由此设定气缸输出拉力为推力的80%。

如图5所示，在换向过程中，气缸输出力矩为：

图5 气缸驱动换向器示意图Fig.5 Diagram of diverter driven by cylinder

式中：Mo为换向器挡板所受气缸输出力矩；Fo为气缸作用在活塞上的力；m为活塞及活塞杆重量；a为活塞及活塞杆加速度；Ff为活塞及活塞杆所受摩擦；l为气缸对换向器挡板作用点距离换向器挡板转轴的竖直距离；θ为换向器挡板与竖直方向的夹角。

以缸径50 mm行程10 mm的气缸为例，活塞与活塞杆的质量经估算约为0.2 kg，而换向器挡板及其一起旋转的隔仓质量经估算约为6.8 kg，活塞与活塞杆质量显著小于换向器挡板及其一起旋转的隔仓的总重量。为了简化计算模型，在后续计算中忽略活塞及活塞杆的质量；活塞及活塞杆所受摩擦在润滑良好的缸内情况下较小，为简化计算模型，忽略活塞及活塞杆质量以及其所受摩擦。

2.2 挡板与流体的相互作用

在换向器的切换过程中，换向器挡板在气缸驱动下开始运动，同时挡板在运动时会受到铅铋流动产生的力矩作用，挡板的运动与铅铋的流动相互耦合，无法单独求解。

本文利用CFD—刚体动力学（Rigid Body Dynamics，RBD）耦合模型对换向器挡板的运动状态进行求解。挡板绕定轴转动，其只存在1个绕x轴的自由度。则挡板的控制方程可由刚体转动方程得到，即：

式中：Ixx为换向器挡板及隔仓对于旋转轴的转动惯量；θ为挡板转动角度；Mx为换向器挡板受到的合力矩。

其中换向器挡板所受合力矩Mx由气缸驱动力矩、换向器挡板所受铅铋的冲击力矩以及挡板运动时的转动摩擦力矩叠加组成，在润滑良好的情况下，转动摩擦力矩较小，可忽略。离散后的代数方程为：

图6 耦合计算流程Fig.6 Process of coupling calculation

2.3 网格无关性分析

2.3.1 喷嘴网格无关性分析

对喷嘴流体域使用网格划分软件FLUENT Meshing划分了4套网格，网格信息如表2所示。对质量流量为100 kg·s-1的工况进行仿真，根据其沿宽度方向的速度分布来检验网格无关性。4套网格计算结果如图7所示，由计算结果可知，当使用网格A3和网格A4计算时，二者之间偏差较小，可以认为网格无关，后续计算使用网格A3进行。

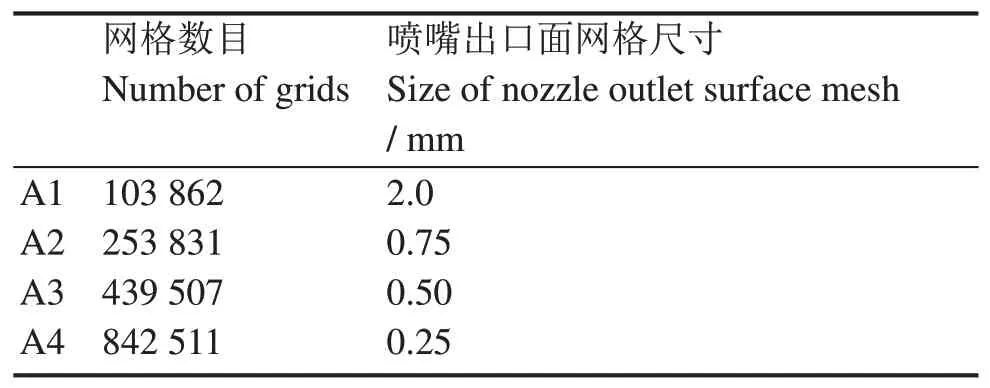
表2 喷嘴网格无关性分析的网格数目及尺寸Table 2 Number and size of grids used in independence analysis

图7 不同网格下喷嘴出口归一化速度分布Fig.7 Normalized velocity distribution under different grids

2.3.2 换向器网格无关性分析

对换向器流体域使用网格划分软件FLUENT Meshing划分了4套网格，网格信息如表3所示。

表3 换向器网格无关性分析的网格数目及尺寸Table 3 Number and size of grids used in independence analysis

对质量流量为150 kg·s-1的工况进行计算，时间步长设定为1×10-4s。在气缸输出力矩已知的情况下，换向器挡板所受冲击力矩决定了挡板的运行速度，进而决定了换向器的B类不确定度分量以及换向器引入的标定相对系统误差，故将换向器未动作时挡板所受力矩作为网格无关性验证指标。4套网格计算结果如图8所示，经计算得到当网格B3和B4计算时，二者之间的偏差在5%以内，可以认为网格无关，后续计算使用网格B3进行。

图8 不同网格下挡板所受冲击力矩Fig.8 Impact torque of baffle under different grids

2.4 时间步长无关性分析

为检验时间步长的无关性，基于上述网格B3选用1×10-4s、5×10-5s、2.5×10-5s三个时间步长对质量流量为150 kg·s-1、驱动力矩为100 N·m的工况下的换向时间进行计算。不同时间步长下的换向时间如图9所示，最大时间步长计算结果与最小时间步长计算结果之间的偏差在0.1%以内，综合考虑计算成本与精度，选用5×10-5s作为后续计算的时间步长。

3 换向器喷嘴出口速度分布

流量工况下的归一化速度（实际速度/喷嘴出口平均速度）在宽度方向的分布如图10所示，各流量下的无量纲速度分布几乎完全相同，主流区速度分布均匀。喷嘴出口左右边界层区内流速分布存在微弱的不对称性，左半部分流量为截面总流量的50.27%。

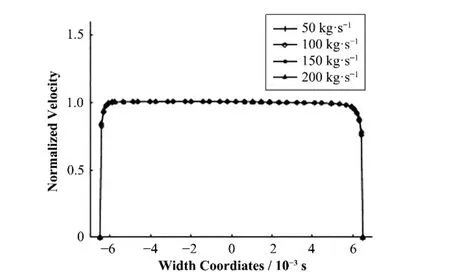
图10 不同工况下喷嘴出口归一化速度分布Fig.10 Normalized velocity distribution under different conditions

4 气缸驱动换向器的运行特性

以150 kg·s-1流量下100 N·m力矩驱动换向器运动的过程为例来分析换向器的换向过程及其特性。换向器挡板所受铅铋的冲击力矩、旋转角度以及旋转角速度如图11（a）、（b）所示。图11（a）中5个时刻挡板所处位置如图12所示。A~E时刻的铅铋相及压力如图13所示。

图11 换向器挡板换向过程中所受冲击力矩(a)，换向器挡板换向过程中的旋转速度与旋转角度(b)（以换向器开始动作为0时刻）Fig.11 Impact torque (a) and rotation speed and angle (b) of the diverter baffle during the commutation process(the diverter starts to move at 0 s)

图12 A、B、C、D、E各时刻挡板位置示意图Fig.12 Diagram of baffle position at moments A, B, C, D,and E

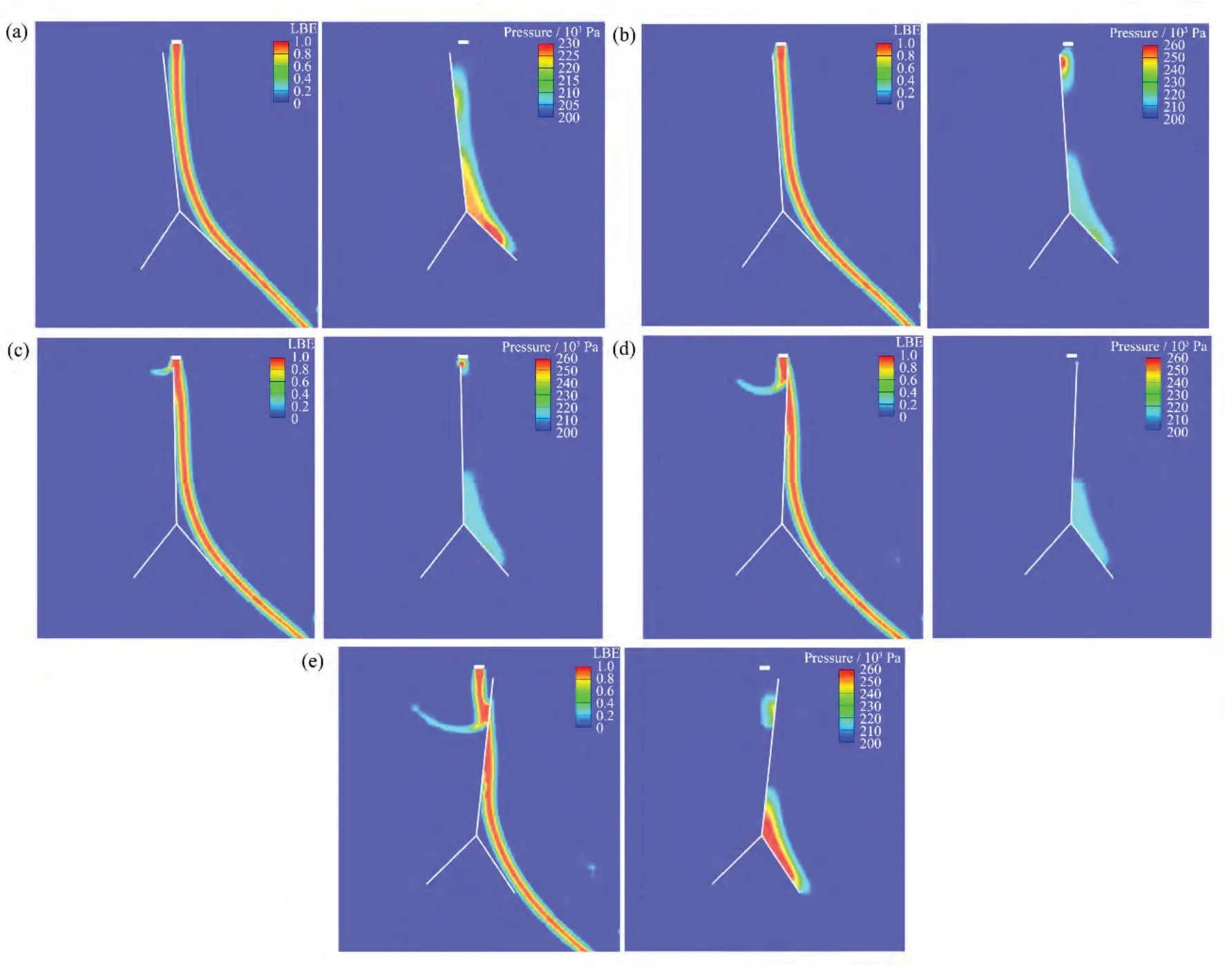
图13 铅铋相图及压力云图 (a) A时刻，(b) B时刻，(c) C时刻，(d) D时刻，(e) E时刻Fig.13 Lead-bismuth phase diagram and contours of pressure at different moments (a) A, (b) B, (c) C, (d) D, (e) E

A时刻换向器开始动作，铅铋主要冲击换向器挡板转轴以下的部分，挡板下部所受冲击压力高于挡板上部，所受总冲击力矩的作用方向与挡板运动方向一致；A时刻至B时刻过程中，挡板并未分割铅铋液柱，但其上端迫使铅铋液柱转向，其受冲击压力逐渐增大，冲击力矩逐渐降低至0然后反向增大；从B时刻运动至C时刻的过程中，挡板开始分割铅铋液柱，挡板右侧上端受铅铋冲击压力逐渐减小，挡板所受冲击力矩逐渐减小到0再反向增大；从C时刻运动至D时刻的过程中，换向器右侧底部所受铅铋冲击压力逐渐减小，所以挡板所受冲击合力矩逐渐减小；从D时刻直至换向结束的过程中，挡板未分割铅铋液柱，右侧上端所受冲击压力逐渐增大，故挡板所受冲击力矩逐渐增大。

在整个换向过程中，因为其所受合力矩与运动方向始终一致，挡板一直处于加速状态。由于换向器挡板减速过程极短且减速过程不参与分割铅铋液柱，对计算结果影响很小，故模拟计算中不考虑换向器挡板的减速过程。

5 换向器的B类相对不确定度

在现行的《JJG 164-2000液体流量标准装置》［10］检定规程中，静态质量法检定装置的装置合成不确定度为：

式中：s1为计时器A类相对标准不确定度；u1为计时器B类相对标准不确定度；s2为衡器A类相对标准不确定度；u2为衡器B类相对标准不确定度；s5、s6为换向器A类相对不确定度；u4为换向器B类相对标准不确定度；uF为砝码相对标准不确定度。

在目前的标定装置设计中，选用的电子秤的合成不确定度为0.076%，计时器的合成不确定为0.016%，为了达到装置的目标不确定度，换向器的设计不确定度为0.03%。

换向器的检定方法一般有行程差法及流量计检定法，其中行程差法中换向器B类相对标准不确定度的计算公式［10］为：

由此可知换向器B类相对标准不确定度由换向时间差决定。不同流量以及不同气缸力矩下的换向器B类相对标准不确定度如图14所示。计算结果显示，在相同流量下，气缸输出力矩越大，换向器正反行程时间差越小，即B类相对标准不确定度越小。在气缸力矩输出一致时，流量越大，行程时间差越小，B类相对标准不确定度越小。这是由于流量越大，换向器在换向初始阶段受到的铅铋冲击力矩越大，使换向过程加速，从而导致换向时间差降低。

图14 各工况下的换向器B类相对不确定度Fig.14 Type B uncertainty components of diverter under various working conditions

6 标定过程中换向器引入的相对系统误差

6.1 流入称重罐的铅铋质量计算方法

如图15所示，当换向器挡板分割铅铋液柱时，流入称重罐的铅铋流量为挡板尖端分割喷嘴出口的左侧面积分流量，所以可以由换向器挡板的运动轨迹计算得到换向器换向时流入称重罐以及流入缓冲罐的质量。图中：d为喷嘴出口宽度；lb为转轴以上挡板长度。

图15 换向器挡板分割液柱时流量统计示意图Fig.15 Schematic diagram of mass flow rate calculation when diverter baffle divides the liquid column

以图15中所示挡板所处位置为例，此阶段流入称重罐的铅铋质量流量为：

式中：ρ为铅铋密度；v（x，y）为喷嘴出口处的铅铋速度分布。

6.2 计时时刻对换向器引入相对系统误差的理论近似分析

关于标定时间的统计方式主要有以下三种：mode A，以换向器行程起点作为计时开始时刻；mode B，以换向器行程终点作为计时时刻；mode C，以换向器行程中点作为计时时刻。

为了便于从理论上推导不同计时方式对标定误差的影响，认为换向器喷嘴出口铅铋速度近似为均匀分布且挡板全程保持匀加速运动，同时由于挡板全程偏转角度较小，将换向器挡板尖端的绕轴转动近似为直线运动，近似后的挡板尖端轨迹如图16所示，图17中A、B、C、D、E时刻挡板位置与图12对应，流入称重罐的质量流量及计量时间如图17所示，图中Δt1为换向器正行程时间；Δt2为换向器反行程时间；m为喷嘴出口铅铋质量流量；M1为换向器正行程中流入称重罐的铅铋质量；M2为换向器正行程中流入称重罐的铅铋质量。则在换向器正行程流入称重罐的铅铋质量：

图16 挡板尖端运动轨迹示意图Fig.16 Schematic diagram of baffle tip movement trajectory

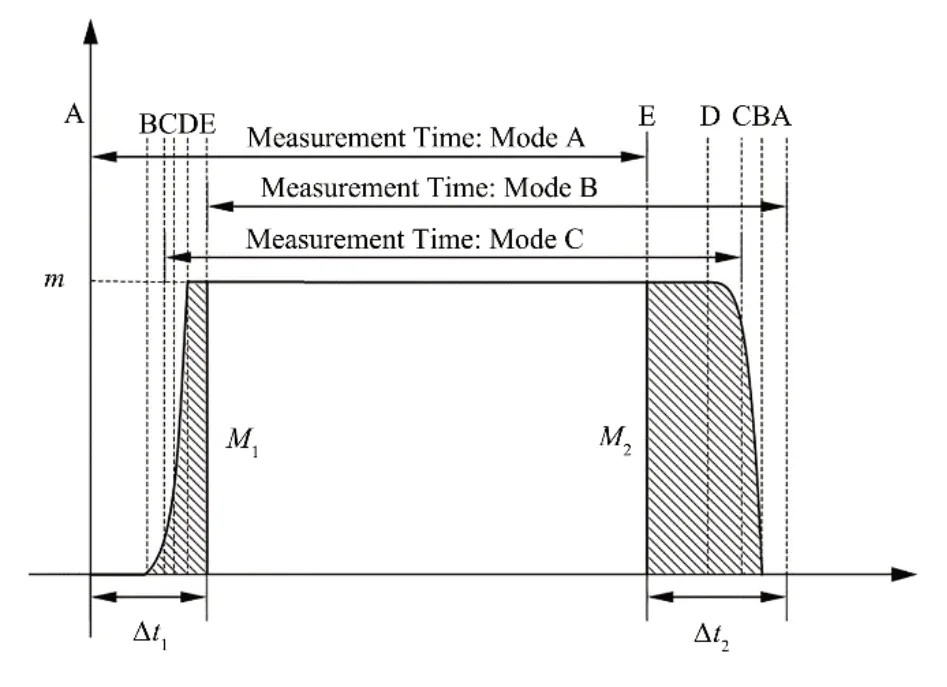
图17 理论上流入称重罐的质量流量Fig.17 Theoretical mass flow rate into weighing tank

式中：a1为换向器挡板尖端正行程加速度。

根据挡板的匀加速运行规律，挡板尖端位到达B、D两点时其位移和时间存在以下关系：

将式（11）、（12）代入式（10）中可得：

同理可得换向器反行程流入称重罐的铅铋质量：

Mode A：当以换向器行程起点作为计时开始时刻时，流入称重罐的总重量为：

式中：Mt为流入称重罐的总质量；tt为测量时间。即：

则换向器引入的绝对系统误差：

其相对系统误差：

Mode B：当以换向器行程终点作为计时开始时刻时，其相对系统误差：

Mode C：当以换向器行程中点作为计时开始时刻时，其相对系统误差：

由上述分析可得，三种计时方式下换向器引入的相对系统误差均不相同，从大到小依次为mode A、mode B、mode C，mode C的相对系统误差显著低于前两者。三者的相对系统误差均为由行程差法得到的换向器B类不确定度分量的倍数，所以由行程差法得到的换向器B类不确定度分量理论上能够反映换向器由于正反行程不对称引入的相对系统误差。

6.3 换向器引入相对系统误差的数值分析

§6.2的理论分析是基于简化假设的，换向器实际运动情况偏离匀加速运动，只适合作为定性参考。为了对该问题进行定量分析，结合§3、§4对喷嘴速度分布、换向器运行动态过程的数值模拟，本节使用数值方法进行分析。

在计算换向器引入的误差时，统一设定标定计时时间tc为30 s，M1、M2分别为换向器正反行程中挡板分割铅铋液柱时流入称重罐的铅铋质量，并假定在标定全程中，喷嘴出口流量保持恒定，无流量波动。

计算结果如图18所示，可知mode A与mode B下各工况点由于换向器引入的相对系统误差随着气缸力矩的增大而减小；mode A下换向器引入的相对系统的误差约为mode B的两倍，与理论推导一致；换向器B类不确定度分量随流量变化的趋势与mode A、mode B下换向器引入的相对系统误差的变化趋势基本一致，换向器B类不确定度分量能够较好地反映相对系统误差的大小，与理论推导一致。将行程中点作为计时时刻的相对系统误差仅为另外两种计时方式的1/7~1/30，由此可见使用行程中点作为计时时刻可以大幅降低换向器引入的相对系统误差。总的来说，由行程差法得到的换向器B类不确定度可以反映不同计时方式下换向器引入的相对系统误差的包络值。

图18 不同工况下换向器引入的相对系统误差Fig.18 Relative systematic error caused by diverter under different working conditions

在数值模拟的真实工况中，挡板的运动偏离了匀加速转动，且喷嘴速度分布并非完全均匀，因此在使行程中点作为计时时刻时换向器仍会引入一定的相对系统误差。根据本节的计算分析，在计算工况下使用行程中点作为计时时刻时最大相对系统误差为5.1×10-6，相对于铅铋流量计标定装置0.33%的不确定度设计指标几乎可忽略。

7 结语

基于CFD方法，本文提出了一种用于开式换向器的双向耦合计算方法，可以预估气缸驱动换向器由于气缸正反行程不对称而造成的系统误差，实现了对气缸驱动换向器B类不确定度的先验评估。基于这种方法和铅铋流量计标定装置开式换向器的模型，通过对不同气缸参数及不同铅铋流量下的换向器运动过程分析，得到了以下主要结论：

1）气缸推力越大，换向器正反时间差越小，换向器B类不确定度越小。

2）相较于采用行程起点或终点作为计时时刻，将换向器挡板运动至行程中点作为计时时刻时换向器引入的标定相对系统误差最低，约为其他两种计时方式的1/7~1/30。

3）换向器B类不确定度的大小可以反映使用不同计时时刻时换向器引入的相对系统误差的包络值。

作者贡献声明朱喻成负责计算方法的提出与实施，起草文章；范旭凯负责计算指导与论文修改；彭天骥负责论文选题与整体设计，计算指导与论文修改，研究经费支持；范德亮负责文献调研；唐延泽、田旺盛负责协助计算。