基于MCMC方法的子通道程序模型参数不确定性量化分析研究
何鑫 宋美琪 刘晓晶,2
1(上海交通大学 智慧能源创新学院 上海 200240)
2(上海交通大学 核科学与工程学院 上海 200240)
相较于保守性安全分析,最佳估算结合不确定性分析能更加真实准确地模拟反应堆运行状况,更适合核电厂的安全裕度分析与性能评价[1]。1989年,美国核管理委员会发布了RGI.157管理导则,允许在应急堆芯冷却系统(Emergency Core Cooling System,ECCS)分析中使用最佳估算程序,但要对计算结果的不确定性进行评估[2]。此后,多种与现实性程序相关的不确定性分析方法被开发出来,如著名的程序缩放模拟、应用及不确定性分析(Code Scaling,Applicability and Uncertainty,CSAU)方法[3]、西屋公司采用的ASTRUM(Advanced Statistical Treatment of Uncertainty Method)方法[4]、德国开发的GRS(Gesellschaft fur Anlagen-und Reaktorsicherheit)方法[5]、意大利开发的UMAE(Uncertainty Method based on Accuracy Extrapolation)方法[6]等,主要可以分为基于输入的不确定性正向传递和基于输出的不确定性外推,前者的发展更为成熟,应用更加广泛[7]。这些方法大多要提前给定不确定性来源的分布,但受制于数值模型近似和认知水平局限,大多数热工水力程序并没有提供足够的与内部模型相关的输入不确定性信息,通常由专家评估给出。
近年来,一些代替专家保守评价的分析方法陆续被提出,如利用快速傅里叶变化来评估输入参数变化范围的FFTBM(Fast Fourier Transformation Based Methods)方法[8]、通过不断调整参数边界来评估程序计算值对实验数据的覆盖率得到参数的伪累积分布函数的DIPE(Determination of Input Parameters Empirical properties)方法[9]、基于线性假设通过EM(Expectation Maximization)算法评估模型参数不确定性的CIRCÉ(Calcul des Incertitudes Relatives aux Corrélations Élémentaires)方法[10],以及通过确定性和概率性数据同化方法求解线性和非线性问题的MCDA(Model Calibration through Data Assimilation method)方法[11]等。Wilks 等[12]利用Metropolis 算法实现马尔科夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)抽样,对收敛到平稳目标分布的马尔科夫链进行抽样统计,从而获得反问题的解。随机论对应着大量的正向计算,因此建立高精度的代理模型来替代复杂的正向程序有着重要意义。李冬等[13]对MCDA 方法的非线性部分进行改进,通过建立高精度的RBF(Radial Basis Function)神经网络代理模型来简化正向计算,并将其应用于再淹没现象中物理模型参数不确定性的评估。Wu 等[14]采用基于高斯过程(Gaussian Process,GP)代理模型的改进模块化贝叶斯方法对TRACE程序的相关物理模型参数进行不确定性分析。
子通道程序是重要的堆芯热工水力安全分析工具,但由于对热工水力模型的认识仍存在欠缺,在相关的设计和安全分析中会采用一些保守估计,导致程序计算结果存在一定不确定性。而现阶段的不确定性分析大多针对系统程序,有关子通道程序模型参数的不确定性量化分析相对较少。本研究采用随机论方法,利用MCMC抽样构造以模型参数不确定性后验分布为平稳分布的马尔科夫链进行抽样统计,并通过相对熵最小化自适应加密训练数据从而构建高精度BPNN(Back Propagation Neural Network)代理模型代替复杂的系统程序,从而对影响空泡份额的模型参数进行了不确定性量化分析。
1 模型参数的不确定性量化分析方法
不确定性分析是指识别和量化影响输出的所有不确定性因素,特别是不能通过实验直接测量的关键模型参数,并基于不确定性的正向传递得到输出结果总的不确定性分布[7]。不确定性的来源[15]有程序模型偏差,数值计算近似,边界条件和初始条件不充分等,其中程序模型对物理现象的近似是不确定性的根本来源。
1.1 模型参数的不确定性量化
不确定性分析需要确定模型参数基准值的无量纲常数k(k=(kj)j=1...p,p指模型参数个数),可用kj=exj表示[16]。其中,x=(xj)j=1...p指模型参数的不确定性,y=(yj)j=1..q(q指实验点个数),表示程序响应的不确定性,不确定性在正向程序中的传递关系可简化为y=h(x)。假设参数之间相互独立,可以用正态分布来描述未知模型参数的不确定,即x~N(μx,Cx)。实验测量值yexp与程序预测值ycode为真实值yreal的求解提供了参考,两者差值ym可用式(1)表示,其中:e指实验误差,且e~N(0,σexp)。
根据贝叶斯原理,模型参数的后验概率ppost(x|ym)可表示为式(2),其中pprior(x)是模型参数不确定性的先验概率密度,p(ym)指可观测误差的概率,可看作常数。L(ym|x)指模型参数不确定性x关于可观测误差ym的似然函数。
本研究通过Metropolis算法实现MCMC抽样求解式(2)。首先,需要构建一个合理的提议函数,并根据接受概率α判断是否保留第t步的采样点x*,x*在x*~N(xt-1,Ct-1)中抽样产生,直至通过循环产生的点构成的马尔科夫链可以稳定收敛到后验分布。接受概率表示为式(3)。
然而,要想得到稳定的马尔科夫链,抽样次数至少达到104数量级,在求解公式(2)时需要调用相应次数的最佳估算程序,这意味着巨大的计算量。为了提高计算效率,可通过BPNN 建立代理模型代替式(2)中的
1.2 BPNN 代理模型构建及训练数据自适应加密
BPNN 对非线性函数的拟合性较好,具有收敛速度快,鲁棒性好,适应性强的优点。BPNN是利用误差反向传播算法进行训练的多层前馈神经网络,它将网络输出的误差平方作为目标函数,利用梯度下降法求解目标函数的最小值实现权值的更新。其中输入层的样本点{x1,x2,...,xn}是在上一步迭代样本空间中通过随机抽样产生,隐藏层采用sigmoid函数,输出层通过运行外部正向程序得到x对应的构成。
为提高代理模型的精度,训练样本点要尽可能在接近后验概率的空间上取到,可利用相对熵最小化在高后验概率空间自适应加密样本点[17]。提议空间ppro(x)与后验概率空间ppost(x|ym)的差异表示为式(4),其展开式的前一项与ppro(x)无关。因此最小化DKL(ppost||ppro)等同于最大化后一项,记为D(θpro),表示为式(5)。可通过来不断更新提议分布的均值与方差,直至满足收敛要求。在建立满足精度要求的代理模型后,给定随机抽样产生的输入样本点x,就可以利用BPNN代理模型得到对应的输出。
1.3 不确定性分析方法验证
本文设置了一个简单算例验证上述方法的准确性,其函数表达式如式(6)所示,其中,x1与x2相互独立,可知其最大概率点位于点(3,4),方差分别是0.4和0.3。
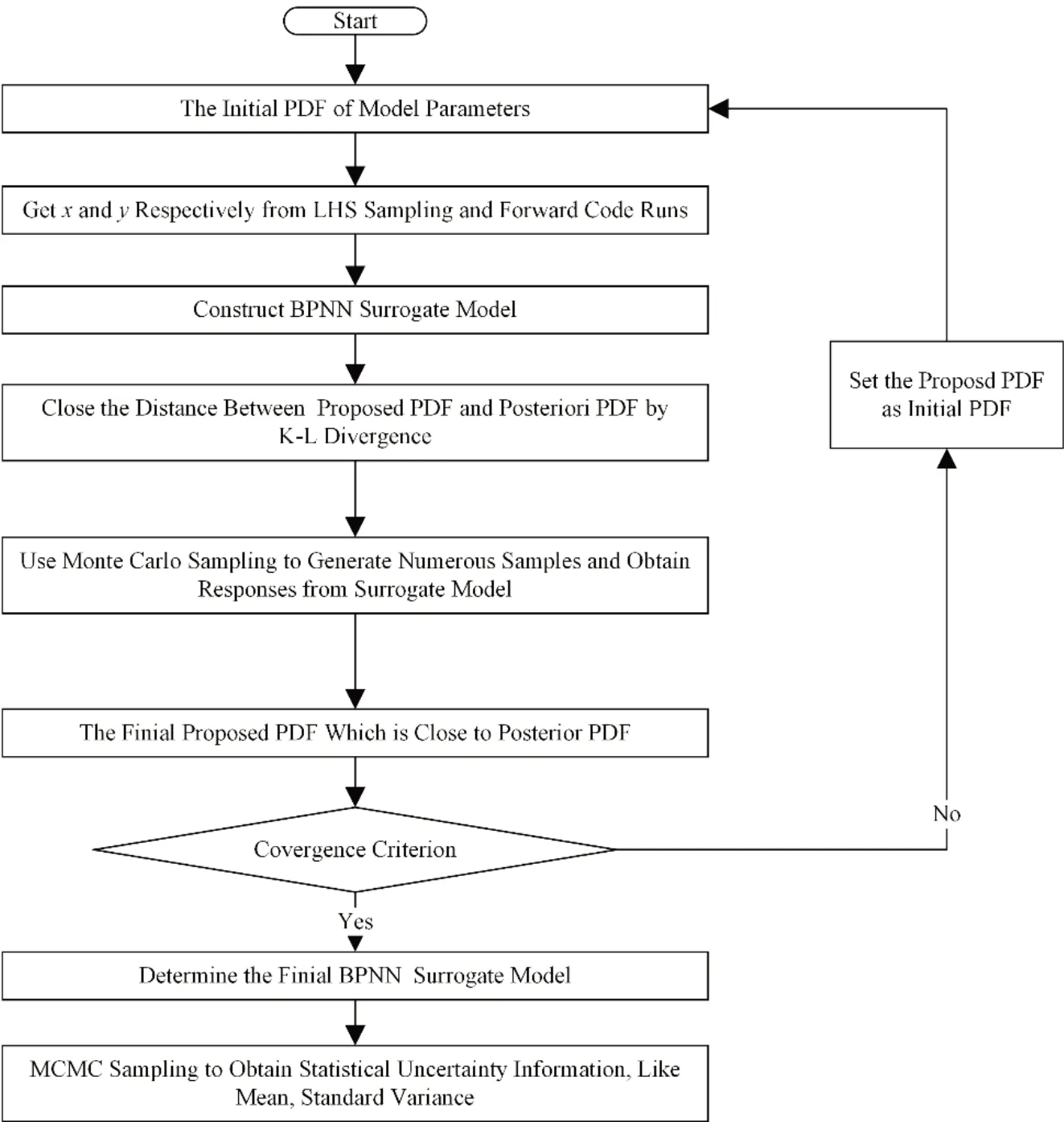
图1 不确定性分析流程图Fig.1 Flowchart of uncertainty analysis
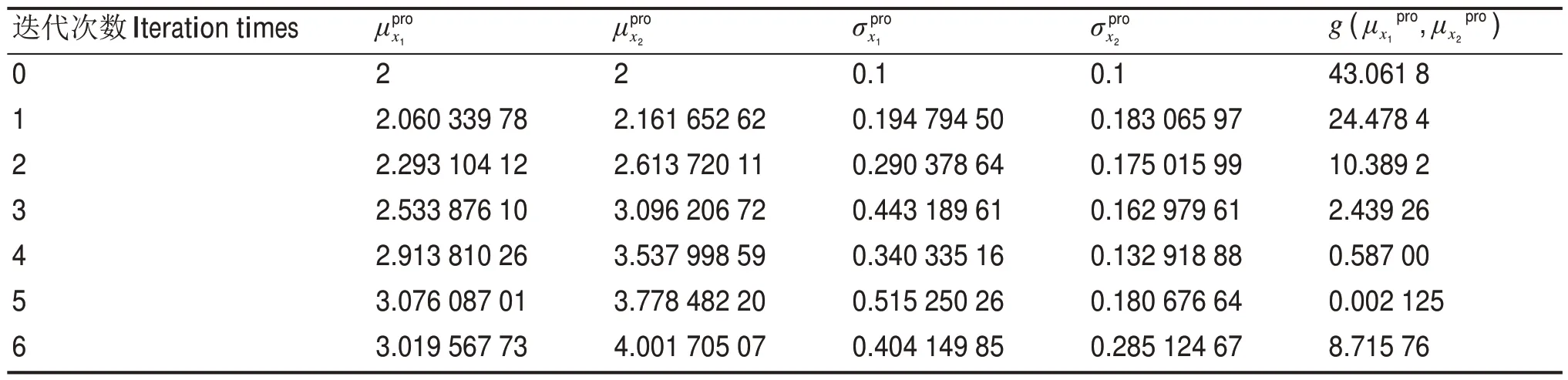
表1 自适应加密过程中的提议参数Table 1 Proposed parameters for adaptive encryption
2 子通道程序不确定性分析
2.1 子通道程序对PSBT 空泡份额实验不确定性量化分析
压水堆子通道及管束试验(PWR Sub-channel and Bundle Tests,PSBT)是OECD/NRC 发布的一套基准,主要用于验证子通道和管束中空泡份额及偏离泡核沸腾(Departure from Nucleate Boiling,DNB),实验数据包括单相流管束出口的温度分布、稳态和瞬态的空泡份额以及临界功率[19]。空泡的存在会影响反应堆堆芯棒束的传热效率,所以能否高效准确地预测空泡份额具有重要意义。
本研究通过子通道程序COBRA-IV 模拟PSBT基准一阶段稳态空泡份额分布,从而对子通道程序的计算能力和不确定性进行分析。选取PSBT稳态工况的30组空泡份额实验数据,其压力变化范围是7.36~14.71 MPa,质量流量变化范围是1 380.6~2 288.9 kg·(m2·s)-1,加热功率变化范围是1 920~3 536 kW,入口温度变化范围是173.5~287.8 ℃。选取其中的25组,利用开发的不确定性分析程序反向量化对空泡份额有重要影响的模型参数的不确定性,在确定模型参数的不确定性后,基于不确定性正向传递的方法,利用另外5 组实验数据对不确定性结果进行评估。
在选用滑移模型作为空泡份额模型时,滑速比和湍流交混系数是影响空泡份额的主要模型参数[20],其他影响空泡份额的边界条件参数不确定性可认为服从均值为0 的正态分布,标准差可通过PSBT 实验测量精度确定,并按照3σ原则进行处理[21],结果如表2 所示。由于多波束系统测量弦向平均孔隙率的稳态精度为±4%,可确定实验误差σexp为4%[21]。

表2 边界条件参数的不确定性分布Table 2 Uncertainty distribution of boundary condition parameters
本研究采用滑移模型,其滑速比可以进行设置。滑速比和湍流交混系数根据如下标准进行选取[22]:根据最小熵增原理可计算14 MPa 下的滑移比为1.86,但通常最佳估算程序的计算值要大于实验测量值;均相模型是最典型的单向流模型,认为气相和液相之间不存在相对滑移,即滑速比为1,因此,最终将滑速比的基准值设为1.2。Castellana实验与本研究选择的工况相似,因此取湍流交混系数的基准值为0.008。
将滑速比和湍流交混系数设置为选定的基准值进行计算,子通道程序的空泡份额预测值和实验测量值的对比如图2 所示,数据点越靠近直线表明程序预测结果与实验结果越接近,两条虚线代表实验误差范围。可以发现整体的预测值要高于实验测量值,尤其是在低空泡份额有很多数据点落在了实验误差范围外,这说明所选用的模型不确定性较大,需要对其进行量化分析。
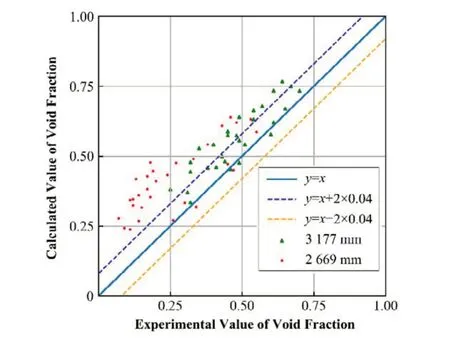
图2 空泡份额实验值与计算值对比图Fig.2 Comparison between the experimental and calculated void fraction values
2.2 模型参数不确定性分析结果
根据图1 的不确定性分析流程图,首先需要确定初次迭代的先验分布,这里两个模型参数服从相同的先验分布,即sprior~N(0,0.1),βprior~N(0,0.1),其中:s为滑速比,β为湍流交混系数。每次迭代的抽样个数为10,选取其中25组实验工况用于模型参数的不确定性分析。将每组工况距离加热底端2 669 mm 和3 177 mm 的中心子通道空泡份额平均值 作 为 实 验 测 量 值 ,建 立g(x) =的代理模型。
利用相对熵最小化原理在自适应加密过程中得到的模型参数的提议分布如表3所示,可以看到,在三次迭代后满足了收敛准则的前一项条件。由于g(x)表示50个样本点的累计误差,以及在计算中还存在着其他的随机误差,模型误差等因素,所以会导致程序计算结果与实验值不会完全重合。采用小批量随机梯度下降法来对BPNN 进行训练,在建立BPNN代理模型过程中每次迭代的网络误差下降曲线分别如图3(a~c)所示。本研究尝试了多种不同的初始先验分布以及每次迭代时采用不同的抽样点数,最终得到的提议参数与表3类似。
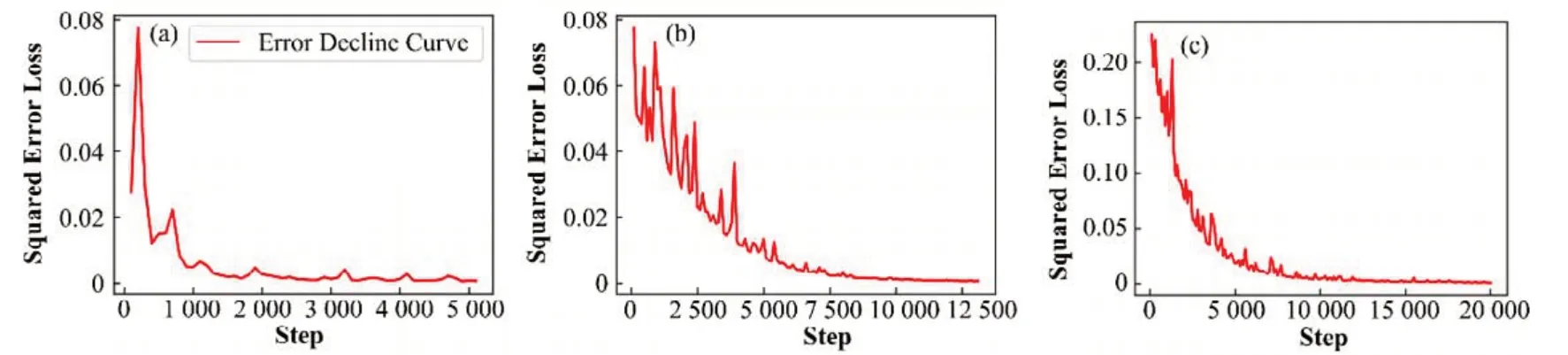
图3 建立BPNN代理模型时的误差下降曲线Fig.3 Error decline curve when establishing the BPNN surrogate model

表3 自适应加密迭代过程中得到的提议参数Table 3 Parameters proposed by adaptive algorithm iterations
在得到满足要求的代理模型后,进行MCMC抽样,设置链长为20 000。为了避免马尔科夫链前期发散,对第5 000~20 000个点进行了统计分析,模型参数不确定性的结果如表4 所示。利用自适应Metropolis 算法得到的滑速比和湍流交混系数的随机样本游走点及频次分布直方图分别如图4 和图5所示。

图4 自适应Metropolis 算法产生的样本路径图 (a) s的样本随机游走,(b) β的样本随机游走Fig.4 Sample path of the adaptive Metropolis algorithm (a) Random-walk samples from s, (b) Random-walk samples from β
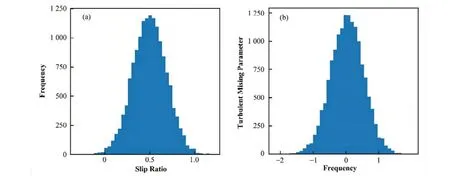
图5 20 000次迭代样本的频次直方图 (a) s的频次直方图,(b) β的频次直方图Fig.5 Frequency histogram of 20 000 iteration samples (a) Frequency histogram of s, (b) Frequency histogram of β

表4 模型参数不确定性分布的均值与标准差Table 4 Uncertainty distribution of the mean and standard variance for the model parameters
通过上述方法得到模型参数的不确定性后,同时考虑模型参数和边界条件的不确定性,利用另外5 组实验数据,基于不确定性的正向传递方法得到计算结果95%的置信区间对实验值的包络性情况。根据Wilks 公式,需要最少93 次抽样才能得到双边容忍限和置信度均为95%的情况[23],可通过蒙特卡罗方法进行不确定性的正向传递,运行93次最佳估算程序,将计算结果的最值作为置信区间的上下限。图6 为双95%置信区间的上下限包络性检验,可以发现,不确定带对实验值的包络性较好。利用模型参数不确定性统计均值对参数基准值进行修正,图7为模型修正值和基准值的计算结果和实验数据的对比,可以看出,修正后的模型预测值较原基准值预测结果更加接近实验测量值,其中模型修正值计算结果与实验值的平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Square Erroe,RMSE)分别为3.356%和4.079%,而基准值计算结果与实验值的MAE 与RMSE 分别为12.028%和12.695%。
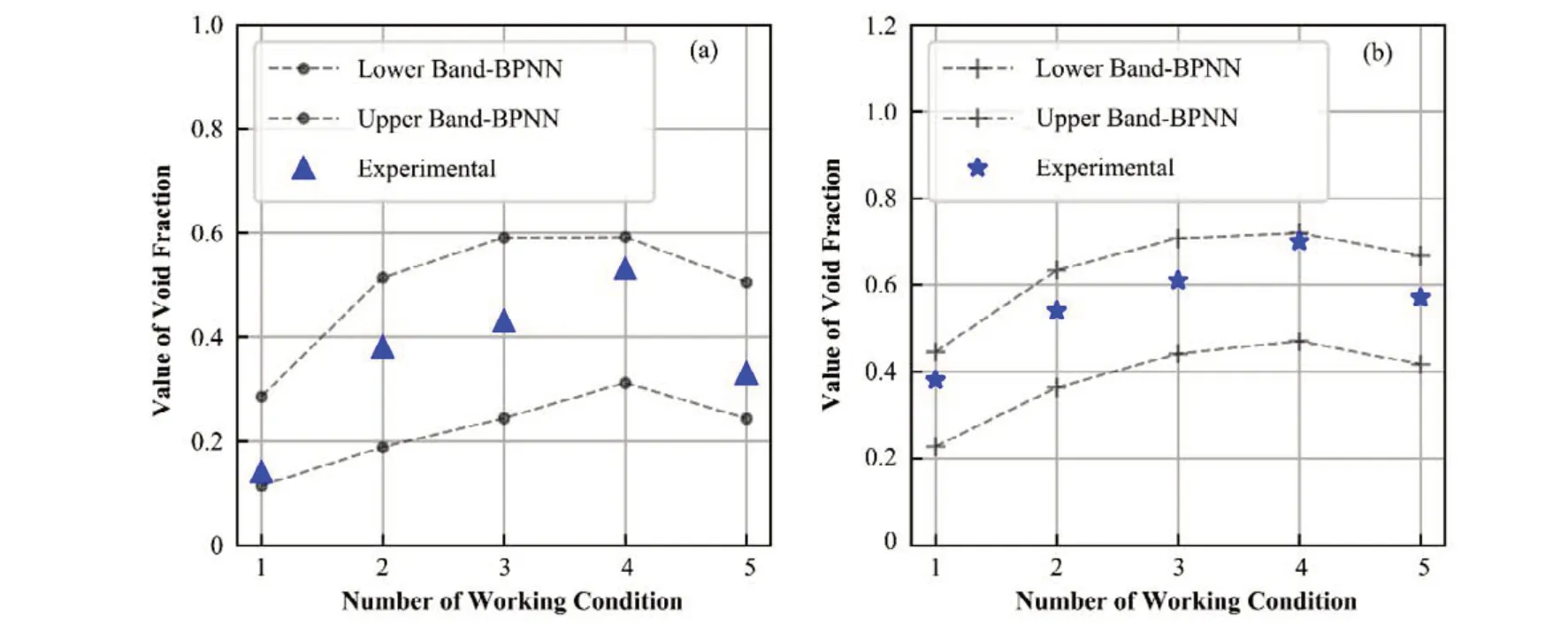
图6 95%置信区间的包络性检验 (a) 2 669 mm测量点的空泡份额,(b) 3 177 mm测量点的空泡份额Fig.6 Envelop test for 95% confidence interval (a) Void fraction at 2 669 mm, (b) Void fraction at 3 177 mm
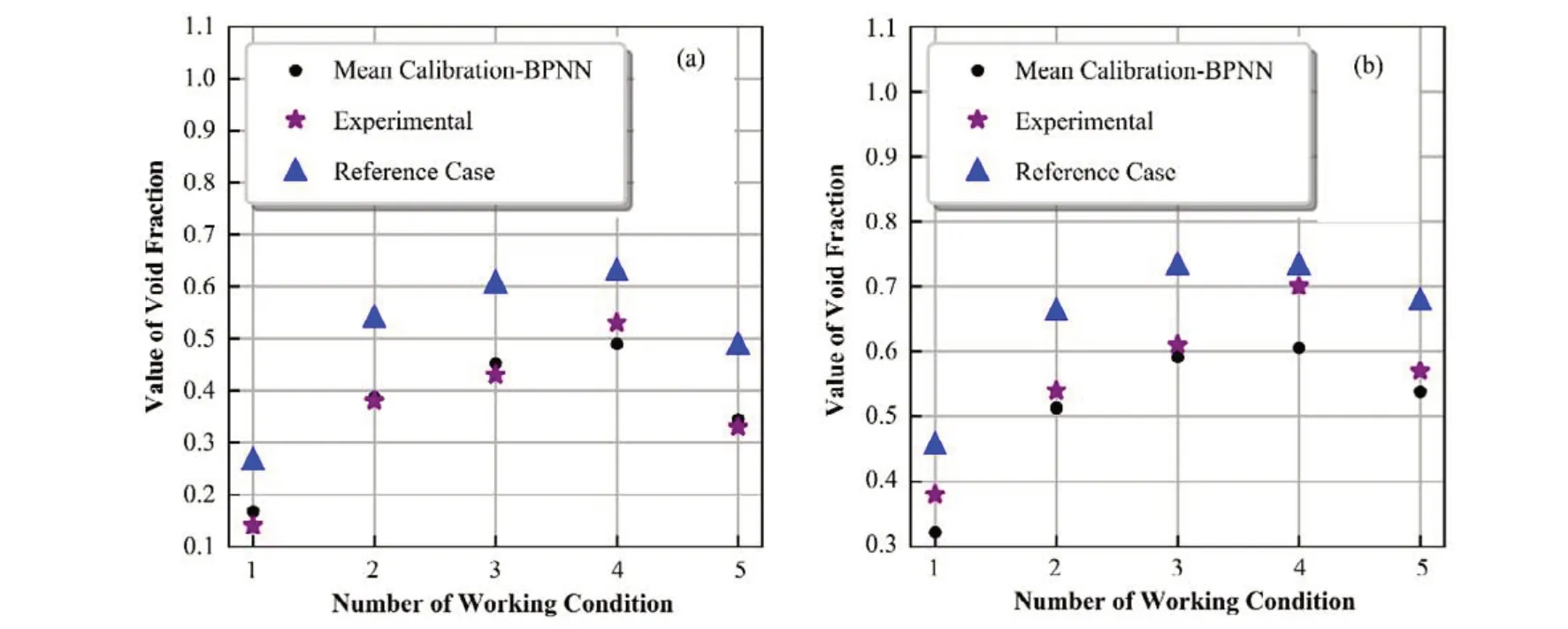
图7 模型参数均值修正后结果 (a) 2 669 mm测量点的空泡份额,(b) 3 177 mm测量点的空泡份额Fig.7 Calibration resultsof the two modified model parameters (a) Void fraction at 2 669 mm, (b) Void fraction at 3 177 mm
3 结语
本研究利用开发的Python 不确定性分析工具同时对多个模型参数不确定性进行分析,得到了滑速比和湍流交混系数的不确定性分布。在所选的计算模型和实验工况范围内,滑速比的不确定性较湍流交混系数更大。得到输入参数不确定性后,基于不确定性正向传递方法,得到了95%置信区间的空泡份额不确定带,并利用模型参数不确定性均值对基准值进行修正,结果表明:
1)原模型基准值预测结果要普遍高于实际测量值,尤其在低空泡份额情况,很多点落在了精度范围外。基于不确定性正向传递方法,包络性检验得到的95%置信区间不确定带对实验值包络性较好。
2)利用模型参数不确定性均值对基准值进行修正,修正后的模型预测结果较基准值预测结果更加接近实验值。因此本研究建立的不确定性量化分析方法能较好适用于子通道程序模型参数不确定性分析,这为后续的子通道程序不确定性研究提供了参考。
作者贡献声明何鑫负责研究方案设计,论文撰写,实施研究,代码编写,采集数据,分析/解释数据;宋美琪负责研究方案设计,对文章的知识性内容作批评性审阅,论文指导与修改,代码调试,实验结果数据分析;刘晓晶负责研究方案设计,获取研究经费,技术支持,论文指导与修改,实验结果数据分析,支持性贡献等。
1D'Auria F, Camargo C, Mazzantini O. Best Estimate Plus Uncertainty (BEPU) approach in licensing current nuclear reactors[J]. Nuclear Engineering and Design, 2012, 248:317-328. DOI: 10.1016/j.nucengdes.2012.04.002.
3Skorek T, de Crécy A, Kovtonyuk A,et al. Quantification of the uncertainty of the physical models in the system thermal-hydraulic codes - PREMIUM benchmark[J].Nuclear Engineering and Design, 2019, 354: 110199.DOI: 10.1016/j.nucengdes.2019.110199.

