澜沧江货船静水航速估算方法

许光祥,段景谦,马超峰,杨雪峰,蔡创,蒋孜伟

(1.重庆交通大学 河海学院,重庆 400074;2.澜沧江244界碑至临沧港四级航道建设指挥部,云南 景洪 666100)

现有静水航速、船舶阻力估算方法中,大多属于经验公式;在对已有经验公式的分析及精度验证中发现:

1)不同船型、不同公式在航速估计中考虑影响因素不同,说明影响航速的因素较多,无统一适用于山区航道船舶的航速公式。

2)不同公式计算方式差异较大,查图、公式计算综合在一起,其中经验系数等的取值往往不适用于国内山区航道。

为探讨影响澜沧江货船静水航速的主要因素及建立合适的估算方法,从现有估算方法的影响因素出发,由简入繁,从相对航速、无因次功载比、阻力系数,以及综合因素4个层面分别对澜沧江流域货船的航速估计进行探讨,并以实船试验结果验证精度。

1 实船试验

为了适应澜沧四级和五级航道工程建设的需要,分别于2021年和2006年开展了500 t级自卸货船和300 t级机动货船的静水航速试验,其测试成果为本文分析资料的主要来源。500 t级试验船试验前刚入水不到半年;300 t级试验船试验时已服务多年,轴系和螺旋桨存在一定磨损。

2次静水航速试验相隔时间较长,且在试验测试细节冗杂、内容较多,为节省篇幅,实船试验具体细节参见文献[8-9]。

1.1 试验船参数

500 t、300 t级试验船相关参数见表1和表2。

表1 试验船主要船型参数

表2 试验船螺旋桨主要参数

1.2 静水航速实船试验

两类实船试验在测试方法、测试水域存在些许差异,但测试内容均包含船舶吃水、排水量、主机转速以及航速等,测试结果见表3。其中主机转速、静水航速采用了直线稳定航段上、下行2个航次的平均值。

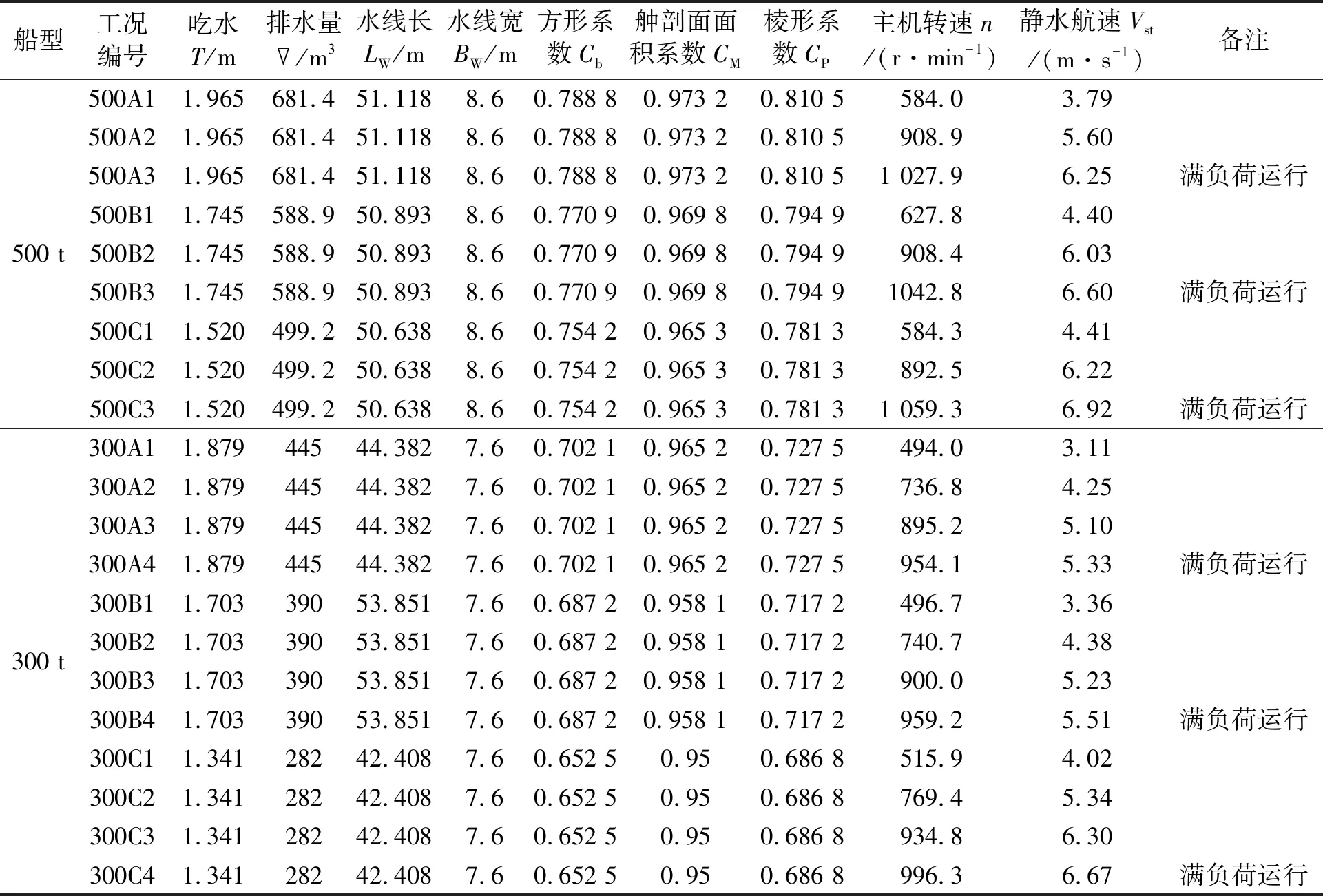
表3 试验船静水航速试验结果汇总

2 现有航速估算方法适应性分析

2.1 估算方法介绍

2.1.1 海军系数法

海军系数法主机功率与航速的关系为[10]

(1)

式中:W为质量排水量,t;C为海军系数,用式(2)估算[12]。

(2)

本文C值范围为65.7～113.9。

2.1.2 巴甫米尔法

巴甫米尔基于船模和实船试验数据,提出了有效功率与航速的关系[11]。

(3)

式中:χ为轴数系数,取1.05;C为经验系数,查图获取,范围为42～101。该法适用于B/T在1.5～3.5之间。

2.1.3 爱尔法

先由标准船型估算有效功率,然后由设计船型与标准船型的差异逐步修正。有效功率与航速的关系为[12]

(4)

式中:C4为设计船型系数,C4=C0+Δ1+Δ2+Δ3+Δ4;C0为标准船型系数,Δ1、Δ2、Δ3、Δ4分别为设计船与标准船因Cb、B/T、xc、LW差异给出的修正增减量,查取相关图表获得,本文C4值范围为70～427。

2.1.4 兹万科夫法

对于无船艉自航船的阻力计算公式为

RV=0.001gf1LW(1.8T+CbB)V1.83+

(5)

式中:RV为船舶阻力,10 N;g为重力加速度;Fr为船舶傅劳德数;其他符号同前。

(6)

上述4种方法从排水量、功率、吃水等参数建立了航速计算公式,分析发现,影响航速的主要参数是排水量、功率。实船试验已获取各工况的参数,但缺乏对各工况主机、有效功率的测算,因此在分析现有航速估算方法适应性之前,对试验各工况的主机、有效功率进行估计。

2.2 有效功率、主机功率的测算

测算功率的思路:先依据试验结果,采用螺旋桨性征曲线推算船舶有效推力Fe,有效功率Pe为

Pe=FeVs

(7)

式中:Vs为船舶对水航速,m/s。

其次将满负荷试验工况主机功率视为额定功率,即作为已知主机功率,以此建立Pe与P的关系,据此反推其他工况的P。

2.2.1 有效推力、有效功率计算

双桨船有效推力Fe为

(8)

式中:ρ为水密度,取ρ=1 t/m3;nx为螺旋桨转速,r/min;t为推力减额分数,采用霍尔特洛泼双螺旋桨船公式;kt为推力系数,由螺旋桨性征曲线查取。

2.2.2 主机功率测算

船舶主机功率与有效功率之间存在如下关系

(9)

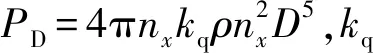
(10)

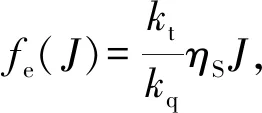
fe(J)=-14.033J3+15.814J2-

3.870 3J+2.281 3

(11)

两艘试验船(1-t)/(1-w)计算值在0.984 66～0.993 76之间,差异不大,故将推进系数e可表达为

e=-1.666 5J3+1.621 6J2-

0.165 8J+0.287 6

(12)

式(12)对试验21组工况的拟合见图1,三次多项式曲线可很好表达e～J之间的关系,e在J=0.6处出现最大值,约0.412。

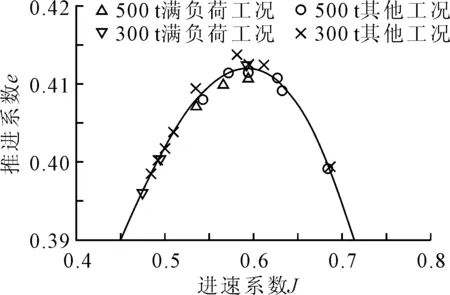
图1 推进系数e随J的变化

最后结合式(7)、(12)及已算出的Fe,由式(9)便可计算非满负荷试验工况的主机功率。

2.3 估算方法的比较

前文已给出试验工况下的有效功率、主机功率计算方法,在此基础上利用4种估算方法计算航速。4种方法计算值与试验值的离散程度见图2、表4。可见,4种航速估算方法直接应用于澜沧江水域货船航速估计偏差很大,适应性非常差。

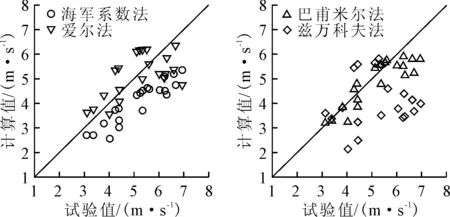
图2 各估算方法静水航速试验值与计算值的对比

表4 静水航速各估算方法计算值与试验值偏差统计

3 静水航速估算方法探讨

基于4种估算方法的主要航速影响因素,由简入繁,探讨澜沧江货船的静水航速估算方法。

3.1 基于相对航速的估算方法

由表4试验数据和计算结果,经回归分析可得试验船静水航速与排水量、主机功率的关系。

1)500 t级试验船。

(13)

2)300 t级试验船:

(14)

式(13)、式(14)表明:试验船的静水航速与主机功率的1/4次成正比,与排水量的1/2次方成反比,同时也能较好地模拟静水航速的变化规律,见图3。

图3 静水航速计算值与试验值的对比

为统一式(13)、式(14)定义船况系数KV=Vst0/V0,Vst0为额定工况的实际静水航速,m/s;V0为设计航速,m/s。一般船况取KV=1;对刚下水的新船取KV=1.06(本文500 t级);对服务多年,轴系和螺旋桨有一定磨损的船取KV=0.9(本文300 t级)。

再令相对航速等于静水航速Vst与设计航速V0之比,将式(13)、式(14)统一为如下相对航速公式。

(15)

式(15)计算值与试验值的对比见图3,偏差范围在-4.82%～6.16%,具有2方面的意义:①对于已知船型的V0、0、P0,可作母型船对类似船型的V、、P之间的关系进行估算;②对澜沧江水域船舶无法自航上滩的情况,可作为减载量分析依据。

3.2 基于无因次功载比的估算方法

主机功率P、排水量、棱形系数CP及船宽吃水比B/T均影响航速,可将静水航速表示为P、、CP、B/T、ρ及g的函数。

Vst=f(ρ,g,,P,CP,B/T)

(16)

以ρ、g、为基本物理量,通过量纲分析可得静水航速函数表达式。

(17)

(18)

式(18)航速计算值与试验测试值的对比见图4,仅一个测点偏差5.65%,其他测点偏差不到±3%,模拟较好。

图4 式(18)静水航速计算值与试验值的对比

式(18)与纳德马力估算公式给出的规律一致,与式(15)相比,不需母型船数据,直接由船舶功率、载重配置和船型参数便可估算静水航速,又考虑了CP、B/T等因子,应用面得到增广。

3.3 基于阻力系数的估算方法

船舶在静水中航行的阻力为

(19)

式中:CD为总阻力系数,含摩擦阻力和剩余阻力系数;其他符号同前。

当船舶匀速航行时,阻力与功率的关系为

Pe=eP=RVVst

(20)

即

(21)

根据适合于内河船舶的卡尔波夫公式[13],船舶湿面积As=(0.074LW/T+5.1)2/3,按此计算21个工况的As=(6.85～7.56)2/3,为了简化计算,将As表达为

As=7ks▽2/3

(22)

ks=0.98～1.08,联立式(21)、式(22),得到

(23)

CT=ksCD,与总阻力系数相当。考虑到CT=CF+CW。摩擦阻力系数CF取1957ITTC公式并考虑粗糙度补贴。

(24)

对于兴波阻力系数CW,先由试验数据通过式(23)反算CT,再按CW=CT-CF获得CW,最后通过实船试验数据进行相关分析得:

(25)

式中:Fr为排水体积傅劳德数,

因推进系数e和排水体积弗劳德数Fr均含有航速Vst,故基于阻力系数估算静水航速需试算,计算步骤可归纳为

2)由船型参数计算t和w。

4)据J按式(12)计算e。

5)按式(24)、(25)计算CF、CW及CT。

6)根据P、等按式(23)计算静水航速

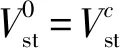
图5表明,计算值与试验值吻合很好,除一个测点外(偏差4.50%),各点偏差在±3%以内。

图5 式(23)静水航速计算值与试验值对比

式(23)与式(18)相比,既考虑了螺旋桨参数及推进特性,又考虑了阻力特性,涉及的因素更全面,应用面得到进一步扩展。同时模拟精度高于式(18),所以基于阻力系数的估算法更为合理。

3.4 基于综合系数的估算方法

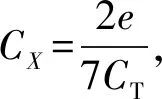
(26)

上式回到海军系数法的式(1),但为保持因次和谐而不采用式(1)的形式。再根据试验数据经回归分析得到综合系数。

(27)

CX包含了船舶推进系数、阻力系数和湿面积系数等,故称之为综合系数。综合系数法的模拟精度仍然较高,各测点偏差不大于±5%见图6。

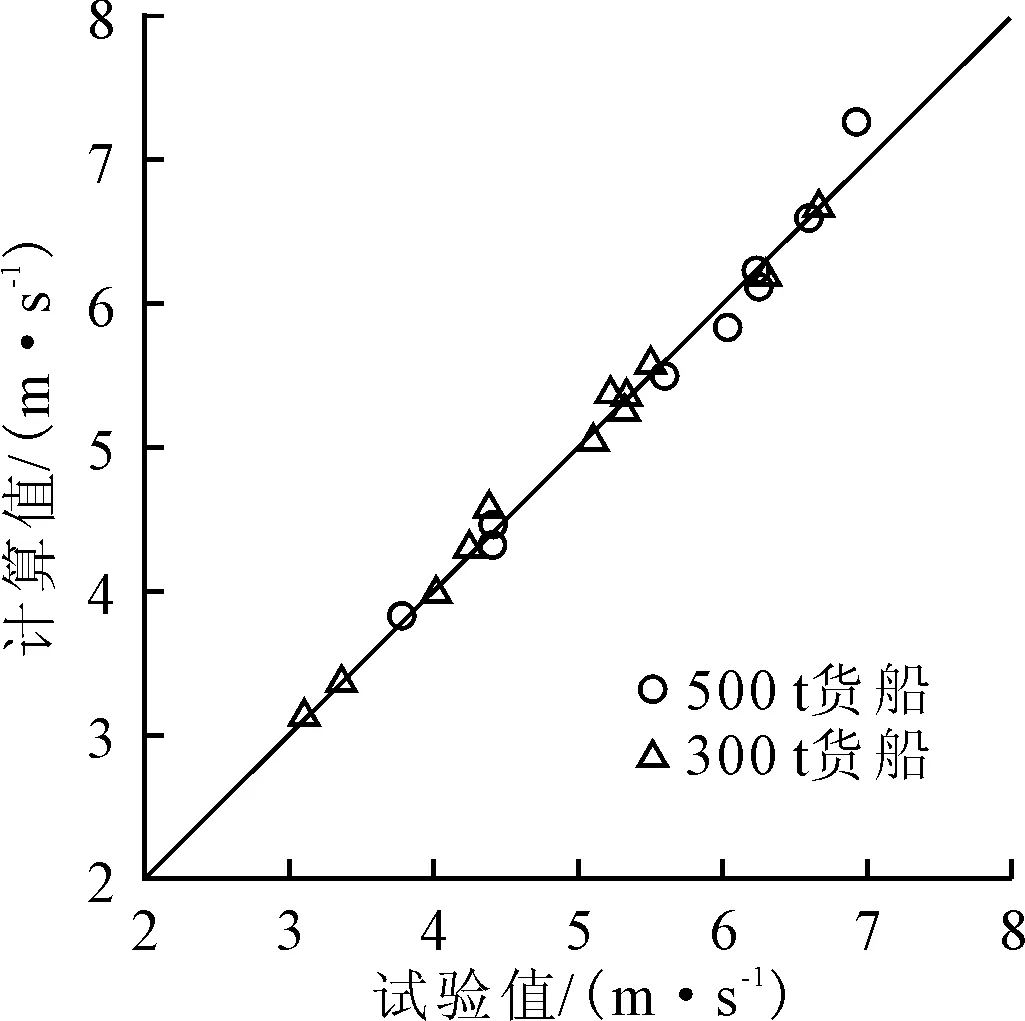
图6 式(26)静水航速计算值与试验值对比

按式(27)计算,CX范围为17～48,换算为海军系数C为127～353,是式(2)计算值的1.5～3.8倍,因此海军系数法计算澜沧江船舶的航速明显偏小。综合系数法式(26)与阻力系数估算法式(23)相比,综合系数法的船舶推进和阻力特性未分开考虑,但计算简便,且精度也能达到要求。

3.5 适用范围

4 结论

1)山区航道货船航速影响因素较多,主机功率、排水量为主要影响因素。实船试验往往难以获取船舶各种功率,基于实船试验数据,提出了推进系数、主机功率等的计算方法。

2)通过海军系数法、巴甫米尔法、爱尔法、兹万科夫法等对试验各工况静水航速的计算,结果与试验数据均存在较大偏差,均不适用于估算澜沧江船型的静水航速。

3)基于相对航速、无因次功载比、阻力系数、综合系数4个层次提出了澜沧江货船静水航速估算公式,可供相近船型静水航速估算、上滩困难减载分析等参考。阻力系数估算法既考虑了螺旋桨推进特性和船舶阻力特性,又考虑了棱形系数、船宽吃水比、船舶傅汝德数的影响,模拟精度相对较高,用于估算澜沧江船型静水航速更为合理。