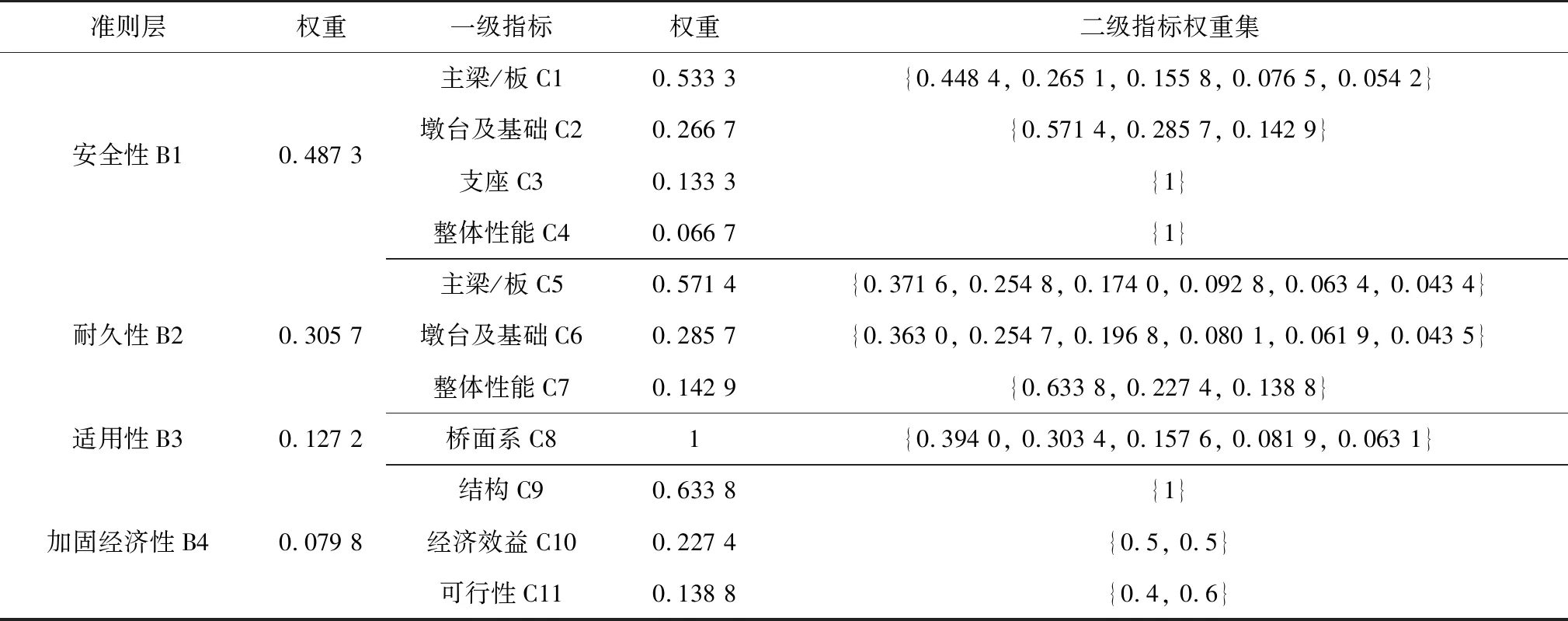
基于BWM与模糊理论的桥梁综合评估方法
李耘宇,张智成,陈金州,彭瀚贤
(1.武汉理工大学 交通与物流工程学院,湖北 武汉 430063;2.武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;3.中交第二公路勘察设计研究院有限公司,湖北 武汉 430212)
0 引 言
受各种因素影响以及随着使用年限增加,我国的旧桥数量急剧增加,耐久性和安全性问题日益凸显,桥梁运营存在极大的安全隐患[1]。这就需要对旧桥进行科学、合理、有效的等级评定;经检测、评估后,对于病害较轻的桥梁可进行一些日常的维护和整治;对于一些病害较严重的桥梁或鉴定为危桥的桥梁,则需要进行加固改造[2]。但是旧桥的各种评价因素信息复杂、散乱,如何科学化、系统化、结构化的评估桥梁综合状态,并提出合理、经济的加固维修措施则显得尤为重要。
为更加准确地评估桥梁的安全性和耐久性,同时便于桥梁评估在实际工程中的操作,可将评估指标权重进行模糊化处理。国内外学者采用模糊综合评估法在复杂桥梁系统病害风险分析、桥梁结构整体安全等级评估方面进行了广泛研究,并取得了一定成果[3-7]。H.G.MELHEM等[8]基于桥梁总体评价程序,通过模糊加权向量法对桥梁整体安全等级进行了评估;A.MIYAMOTO等[9]通过对过往桥梁评估方法进行回顾,利用模糊桥面状况评价法分析了桥面板的构建情况;H.FURUTA等[10]基于遗传算法和神经网络法,研发了桥梁损伤模糊评价的专家系统;兰海等[11]基于变权综合法和灰色关联分析法,确立了桥梁损伤评价的底层指标;禹智涛等[12]采用多级模糊综合评估法分析了既有桥梁的可靠性,并构建了相应的评价体系。
桥梁结构复杂,由多种构件组成,各项指标权重值会对整体评估结果产生很大影响。BWM(best worst method)是一种全新的解决多准则决策问题(MCDM)的方法,该方法被广泛应用于供应链、金融等诸多领域的评价体系中。S.GHAFFARI等[13]采用该方法来评估技术创新发展中的关键因素;W.AHMAD等[14]采用该方法对影响油气行业供应链的外部因素进行了评估,用来指导油气公司识别可能驱动(阻碍)其实施SSCM(可持续供应链管理)的外部力量。国内学者主要是采用该方法进行各方案的比较决策[15-16]。除此之外,BWM法还可与模糊理论相结合,利用模糊集、三角模糊数、区间数等来反映BWM中的不确定性,提高决策者表达观点的准确性[17]。
基于此,笔者以梁板式危桥等级状况评定为重点研究内容,对中小型梁板式危桥的典型病害进行了评估,并提出了加固方案。考虑到梁板式旧危桥实际数量多及结构复杂的特点,为满足高效、准确、客观的评估需求,构建了旧桥综合评价体系,提出了以模糊理论为基础的评估模型,结合BWM法确定了旧桥等级;针对桥梁的不同状态,采用BWM法对加固方案的优先级进行了选择;并将该评估模型应用于丁家桥的综合状态评估中,取得了很好效果,所提出的加固方案对工程实践提供了依据。
1 桥梁综合评价指标体系
桥梁结构综合评价指标体系需要对各构部件进行定量测定或定性分析,综合考虑各构部件损坏情况、重要性等因素,最终确定桥梁整体状态的等级评定。结合调研的旧危桥,构建的综合评估模型准则层为:安全性、耐久性、适用性和加固经济性。
桥梁安全性是指桥梁在正常运营中是否能满足整体的稳定性;耐久性是指在桥梁自身结构是否能在维护、保养和使用下满足原本设定的功能要求;适用性是指桥梁工作性能是否能在运营中保持一个良好的状况;除此之外,还应考虑加固改造的经济性。构建的桥梁综合评价指标体系如图1。
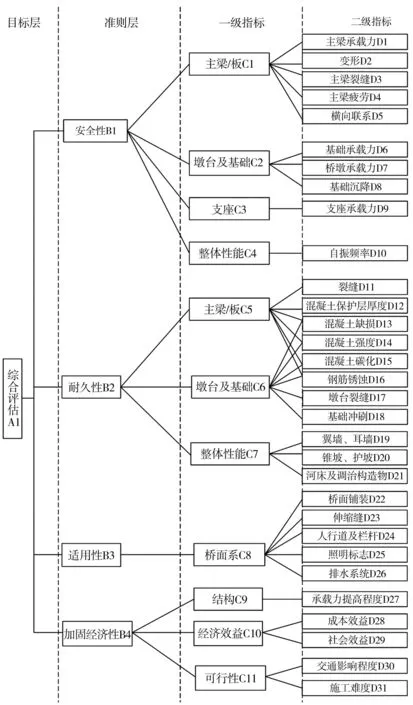
图1 桥梁综合状态评估体系
2 评估理论及模型
2.1 BWM法与实施步骤
BWM法是一种多准则决策方法,它基于一种结构化的成对比较方式,能将定性因素定量化,从而科学、准确的确定不同因素的权重。
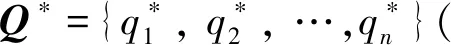
qj≥0, for allj∈N
(1)
式中:qB、qW分别为最优、最劣因素权重值;qj为任意因素权重值。
一致性是判断偏好度的逻辑正确性和结果可靠性重要指标,由式(2)对偏好信息一致性比率CR进行计算:
(2)
式中:CI为一致性指标,取值见表1。
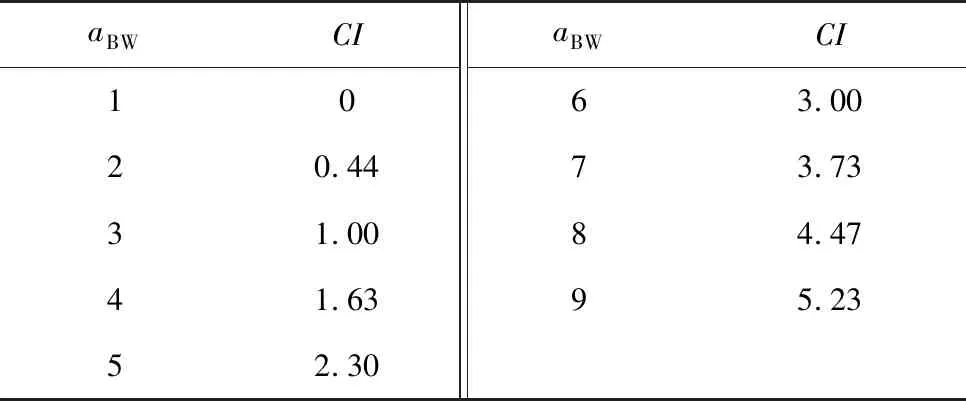
表1 一致性指标
CR∈[0, 1],当CR=0时,可认为偏好信息为完全一致;CR越大,其一致性程度越低;当CR<0.1时,其偏好信息满足一致性要求[15]。
2.2 模糊统计及隶属函数
基于我国现行的规范和标准,笔者将钢筋混凝土梁桥的服役状态评估划分为5个等级,评估等级向量V={v1,v2,v3,v4,v5}。
将指标子集因素ui与评域指标集vj(1≤j≤5)以隶属函数f(u)构建映射关系。当ui完全属于vj时,f(u)=1;当ui完全不属于vj时,f(u)=0;当ui处于中间状态时,f(u)=f(u)。
基于模糊理论,假设底层因素集中的第i个因素为ui,对评估集中第j个指标vj的隶属度为rij,其值可由隶属函数求出。考虑到隶属函数在桥梁评价体系中具有模糊性、实用性、准确性,同时为了兼顾相邻等级之间的影响,笔者在限值对应范围内拟采用半梯形和梯形及梯形隶属函数,如式(3)~式(5);对应的函数分布如图2。
(3)
(4)
(5)
此外,隶属度rij还需满足:
(6)
可用模糊评价矩阵R表示多因素评判集合:
(7)
2.3 基于模糊理论的BWM综合评估模型
以图1中的桥梁综合状态评估体系为基础,建立基于模糊评估理论的BWM综合评估法,从而来判定桥梁状态。其中:底层(实测)因素可利用模糊统计和隶属函数模型来计算隶属度rij;层级各个因素权重值qj由BWM方法计算得到。故某层级某因素的评估向量可由下层各因素权重与下层模糊评价矩阵得到,如式(8)。
(8)
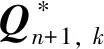
由此构成各层级模糊综合评判集,并按至下而上的顺序逐层传递,最终可得到目标层的最终评估向量。
3 桥梁评级及加固优先级
3.1 桥梁评估等级
根据JTG H11—2004《公路桥涵养护规范》[18]规定:将桥梁评估等级分为5级,1级桥梁为最优,5级为最差,以此来判定桥梁的综合状态,并制定维护或重建方案。
将基于桥梁综合评估模型得到的最终评估向量设为r0,此时根据V和r0,得出桥梁的最终评分向量P=(p1,p2,…,pn),如式(9):
(9)
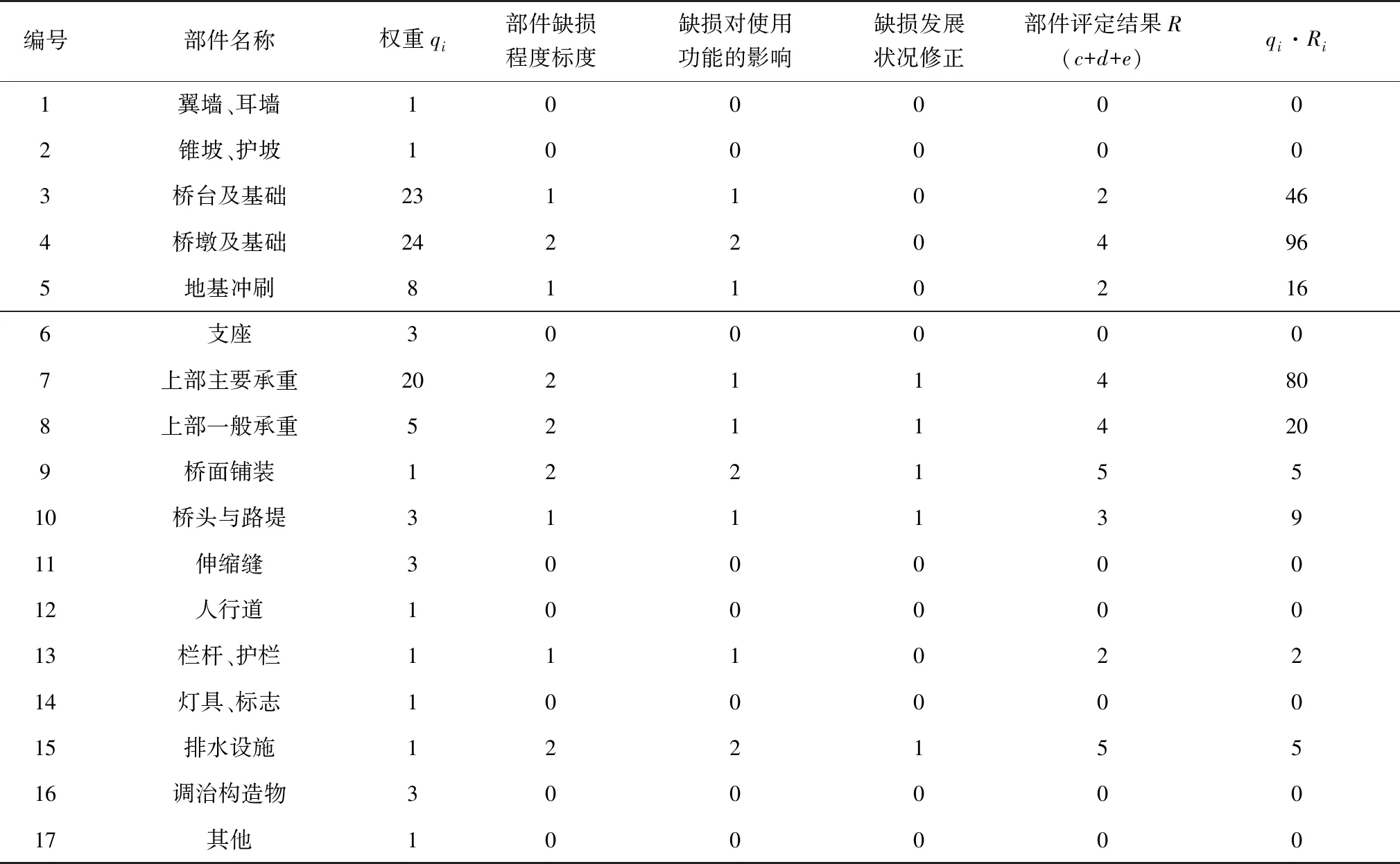
pi越大说明桥梁安全隐患越大(即桥梁等级越高)。由此可对桥梁进行等级评估:若v1 桥梁评级可全面完整地反应出桥梁的整体健康状态。但是中小跨径梁板式桥梁常位于乡镇,易受到地方经济、施工条件等影响,不具备将桥梁完全维修的能力。故应明确桥梁各损坏构件的重要度,优先处理重要度较高的损坏构件。 根据桥梁综合评估模型,提取各层级因素评估向量rn, k。 (10) 由此可得到对应的因素评分pn, k。其中:qn, k为第n层第k因素对应的权重值。采用自上而下方式,获取各层级评分最大值Max{p1,p2,…,pn}(i=1, 2, …,n)对应的un直至底层,则该因素为最重要因素,应优先处理。 丁家桥是一座位于襄阳市的T梁桥,桥梁全长18 m,桥宽6.2 m,原设计荷载等级为汽车-15级。丁家桥病害遍布于桥面系、上部结构和下部结构,具体病害有:桥面铺装出现纵横向裂缝,上部结构多处有明显渗水现象,渗水处伴有白色物质析出,T梁底部多处纵横向裂缝,墩底部冲刷,如图3。 图3 桥梁病害 基于BWM模糊评估算法对丁家桥进行桥梁等级评定并确定其加固的优先级。根据现场实测及实际情况,由式(3)~式(5)确定主梁C1下层因素的模糊评价矩阵RD,C1为: 对主梁下层权重进行分析,拟定D1为因素集的最优量,D5为最劣量,构造最优准则向量AB=(1, 2, 4, 6, 8),最劣准则向量AW=(8, 5, 4, 2, 1)T。 以此类推,可得出各层模糊矩阵、最优权重值及评估向量。目标层最终评估向量为rA, A1=(0.031 5, 0.224 7, 0.514 8, 0.229 0, 0);层级因素最优权重整理如表2。 表2 基于BWM法各层指标最优权重 得到桥梁的综合评估向量后,由式(9)计算出P=2.941 3,即该桥梁等级评估为第3级,考虑到桥梁的安全性,根据3.1节中所述,丁家桥按照2B级进行加固,即应按照三级桥进行加固。由表2可知:桥梁准则层指标权重依次为0.487 3, 0.305 7, 0.127 2, 0.079 8;由式(10)可知:p1=1.420 7,p2=0.883 8,p3=0.382 9,p4=0.253 8;故对该桥梁加固时应先考虑桥梁的安全性指标。根据文献[18],对丁家桥进行技术状况评定,见表3。 表3 丁家桥技术状况评定 由表3可得出评定结果如式(11): (11) 对比表2、表3可知:使用文献[18]的评定结果与文中算法的结果一致,但文献[18]复杂且繁琐,各指标之间关联较弱,打分易出现逻辑混乱,受专家主观因素影响较大,评级易出现较大误差。 笔者结合混凝土梁板式桥的材料特性、结构与受力特点以及评估要素和指标,建立了混凝土梁板式桥结构的评估体系,将多准则决策法(BWM法)与模糊评估算法相结合,利用非线性规划得到了层级最优权重值,并进行多级模糊运算,最后利用最终综合分值来判断桥梁状态等级,通过层级分值确定桥梁构部件的重要度从而进一步确定加固顺序。通过对某旧桥进行实例分析,证明了该方法能较好地反映出桥梁的安全等级,科学的量化层级分值,并得到桥梁加固的优先级,这为桥梁维修与加固提供了科学依据与实践经验。3.2 桥梁加固优先级
4 实例分析


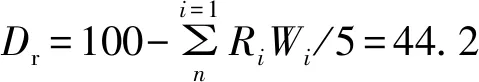
5 结 语

