原位土对道路生物滞留设施水文效应影响研究

刘 燕,潘俊奎

(1. 重庆交通大学 经济与管理学院,重庆 400074; 2. 河南城建学院 土木与交通工程学院,河南 平顶山 467036)

0 引 言

随着城市硬化面积急剧增加,雨水入渗量显著减小,这不仅使得降雨的汇流时间缩短、雨洪峰值增加,还会引起城市水涝灾害频发,导致城市区域的地下水无法得到有效补给,造成城市地下水位逐年下降[1]。另外,城市地表径流通常含有固体悬浮物、有机物、重金属、氮磷营养物等污染物质,这些污染物随着城市排水系统流入下游水系,会对区域的水环境产生负面影响[2]。

随着全球水环境的持续恶化,解决城市雨水问题的相关技术和措施应运而生。生物滞留设施(以下简称:设施)是一种极具应用前景和实用性的雨水生态控制技术[3],其将景观、径流控制及水质净化等功能融合于一体[4-5]。

近年来,学界通过相关试验对设施的水文表现进行了研究。如:PAN Junkui等[6]、R．A．TIRPAK等[7]均证明了设施能有效减少径流水量及径流峰值,延长径流峰现时间,缓解区域径流压力。设施的水文效应也受降雨特征及设施设计参数等多种因素影响。如:S．GÜLBAZ等[8]、高建平等[9]均发现:高强度和长历时降雨会导致设施表层积水深度及穿孔管出流峰值显著增大;GAO Jianping等[10]指出:增大设施的规模、蓄水层深度、填料层厚度能提高区域的年径流水量消减率,有利于实现LID(low-impact development)的控制目标;J．P．JOHNSON等[11]指出:通过设置内部储水区,设施可更好地减小径流水量、消减径流洪峰及延长径流滞留时间,具有更好的水文表现。

数值模型可为设施的规划、设计及研究提供良好辅助。目前,只有RECARGA、HYDRUS-1D、SWMM、SUSTAIN、VADOSE/W等少数模型可用于模拟设施的径流处置过程。RECARGA模型采用Green-Ampt方程来模拟水分渗透过程,但其主要适用于长期的水量平衡分析,不适合模拟设施在短历时降雨下的水分运移过程,同时也无法任意指定渗滤材料的水力参数,从而限制了该模型的广泛应用[12]。HYDRUS-1D模型采用Richards方程进行水分运移计算,作为一维模型,忽略了土壤水分的侧向扩散,也无法模拟存在内部储水区时的水分运移情况[13]。SWMM和SUSTAIN模型简化了设施结构设计及水分入渗过程,主要用于整个区域的LID规划及径流过程模拟,在进行单独的设施研究时存在明显不足[14-15]。VADOSE/W模型是二维模型,能有效分析道路生物滞留带在降雨径流作用下的积水、产流过程[9],证明了该模型可有效模拟设施的水文效应。

近年来,设施在许多个国家和地区被推广应用。但不同地区的原位土特性存在明显差异,若不考虑原位土情况盲目设置设施,则可能会导致运行效果不佳,达不到预期目标;故原位土对设施的水文效应影响还有待于进一步加强研究。基于此,笔者基于VADOSE/W模型,对雨水径流在设施和原位土中的饱和-非饱和运移过程进行了分析,研究了原位土类型对设施的表层积水、穿孔管产流、外渗、径流调控的影响特性,为设施在不同区域的应用提供了理论依据。

1 研究方法

1.1 生物滞留设施的设置

典型的设施横断面如图1。

设施通常由15～30 cm蓄水层、5～8 cm覆盖层、30～70 cm种植填料层、15～30 cm砂砾排水层、溢流装置及植物等组成,设计规模一般为汇水面积的5%～10%。当原位土渗透系数低于1.27 cm/h或设施防渗时,砂砾层中通常会埋设直径5～10 cm的穿孔排水管,以加强设施排水[16]。降雨期间,当雨水径流流经设施时,设施填料层会对雨水径流起到截留、储存作用,一部分径流可缓慢渗入周围土壤以补充地下水,另一部分则在降雨结束后通过蒸发和植物蒸腾作用向大气扩散。

1.2 VADOSE/W模型

VADOSE/W是模拟土壤在饱和-非饱和状态下蒸发、渗流、地下水变化及植物蒸腾作用的二维数值模型。包含了土壤蒸发、径流入渗、水的冻融、气体传输等模块,可模拟多种因素共同作用下对土壤环境的影响。VADOSE/W模型采用Richards控制方程进行复杂的土壤水分运移计算,同时考虑了多种源汇项及边界条件影响,如大气积水边界条件可用于模拟水分在设施表层的累积过程。

1.3 饱和-非饱和土渗流方程

设施的土壤填料长期处于干湿循环状态,为饱和-非饱和土,其水分运移通常包括向下入渗及侧向扩散,可看成二维渗流。因此用二维Richards控制方程来描述设施的水分运移过程,如式(1)。

S(x,z,t)

(1)

式中:h为土壤负压水头,mm;k(θ)为土壤渗透系数,mm/min;θ为土壤体积含水量,mm3/mm3;S(x,z,t)为源汇项(如蒸腾、蒸发),mm,当历时较短时,S(x,z,t)=0;t为时间,min。

式(1)中,当h≥0时,土壤为饱和状态,此时,θ为土壤饱和含水量,k(θ)为土壤饱和渗透系数;当h<0时,土壤为非饱和状态,θ、k(θ)均为变值,θ由土壤水分特征曲线计算,如式(2),k(θ)由水力传导曲线计算,如式(3)。

(2)

(3)

式中:θr为残余含水量,mm3/mm3;θs为饱和含水量,mm3/mm3;a,n,m均为拟合参数,m=1-1/n;Se为有效饱和度,Se=(θ-θr)/(θs-θr);ks为饱和渗透系数,mm/min。

1.4 设计降雨

在进行设施的水文效应研究时,应首先确定设计降雨这一指标。为保证雨水径流有充足时间及水量可穿透设施的填料层,笔者采用暴雨强度公式对一年一遇6 h的设计降雨进行计算,如式(4)。计算中:降雨历时为6 h,降雨强度为0.174 mm/min,降雨总量为62.59 mm,为均匀雨型。

(4)

式中:q为降雨强度,mm/min;t为降雨历时,min;P为降雨重现期,a。

进入设施的水量包括汇水区径流和直接作用在设施上的降雨,其等效降雨强度计算如式(5)。

(5)

式中:q0为等效降雨强度,mm/min;Ψ为径流系数,Ψ=0.9;F0为汇水区面积,m2;F1为设施面积,m2。

1.5 参数确定

1.5.1 设施的设计参数

为研究原位土类型对设施的水文效应影响,笔者采用VADOSE/W模型对设施在4种原位土下的水分运移过程进行了模拟。

4种原位土类型分别为淤泥质壤土(SL)、壤土(L)、砂质黏壤土(SCL)、砂壤土(SaL)。设施设计均取为汇水区面积的10%,蓄水层深度为20 cm,覆盖层厚度均为5 cm,种植土层厚度均为70 cm,砂砾层厚度均为30 cm;当原位土为SL、L时,其渗透系数低于1.27 cm/h,因此在砂砾层中部设置直径为5 cm的穿孔排水管,以形成高度15 cm的内部储水区;当原位土为SCL、SaL时,则不设置内部储水区。

本研究模拟的历时较短,蒸发和植物蒸腾水量可忽略,因此未考虑植物影响。此外,设施的覆盖层通常采用碎树皮或砾石,其渗透系数较大,可视为种植土层上的蓄水层,因此在模拟中未设置覆盖层,但其有效孔隙可叠加至原蓄水层,覆盖层有效孔隙率取0.76,故在模拟时蓄水层高度可设置为23.8 cm。

1.5.2 土壤水力特征参数

在模拟设施的原位土非饱和水分运移过程时,应确定填料和原位土的土壤水力特征参数,如表1。本研究中,设施的种植土、砂砾层土壤水力特征参数采用文献[9]的数据,原位土水力特征参数采用文献[17]的数据。设施填料和原位土初始含水量为介质在饱和状态下自由排水达到稳定后的含水率分布状况。

表1 设施及原位土的土壤水力特征参数

1.6 数据分析

设施对单次降雨径流的调控效果可采用径流量消减率、 径流峰值消减率、 产流延迟时间等3个指标来描述,如式(6)～式(8)。

(6)

(7)

Rdelay=tout-tin

(8)

式中:RV为径流水量消减率,%;Vin为径流水量,mm;Vout为设施总产流量,包括溢流水量及穿孔管产流量,mm;Rpeak为径流峰值消减率,%;qpeak-in、qpeak-out分别为设施进流、出流(包括溢流及穿孔管产流)峰值流量,mm/min;Rdelay为产流延迟时间,min;tout、tin分别为进流和出流(包括溢流及穿孔管产流)的开始时间,min。

2 结果和讨论

2.1 原位土对设施表层积水的影响

在一年一遇6 h降雨作用下,4种原位土类型设施的表层积水情况如表2。由表2可知:表层最大积水时长为547～605 min,最大溢流水量为23.85～38.49 mm。对于SL、L,原位土渗透系数较小,设施底部设置了穿孔排水管,在底部汇集的雨水可从排水管排出,因此这两类原位土类型对表面积水的影响相对较小;对于SCL、SaL,原位土渗透性能对表层积水影响比较明显,且渗透系数越小,表层积水时长越长,溢流水量也越大,这主要由于SCL的渗透系数虽大于SL和L,但相较于种植土而言要小很多(约为种植土的0.25倍),且未配置穿孔排水管,渗入设施的水分易在设施内部累积,进而影响雨水入渗,延长积水时间,增加溢流水量。SaL渗透系数与种植土相差不大,水分更容易扩散至原位土中,导致最大积水时长相对更短,溢流水量也明显减小。由此可见,当原位土渗透系数相比种植土层小很多时,适当配置穿孔排水管可在一定程度上预防设施发生冒顶,降低设施溢流风险。

2.2 原位土对设施穿孔管产流的影响

在一年一遇6 h降雨作用下,SL、L这两种原位土类型(SCL、SaL未设置穿孔排水管)的设施穿孔管产流情况如图2。

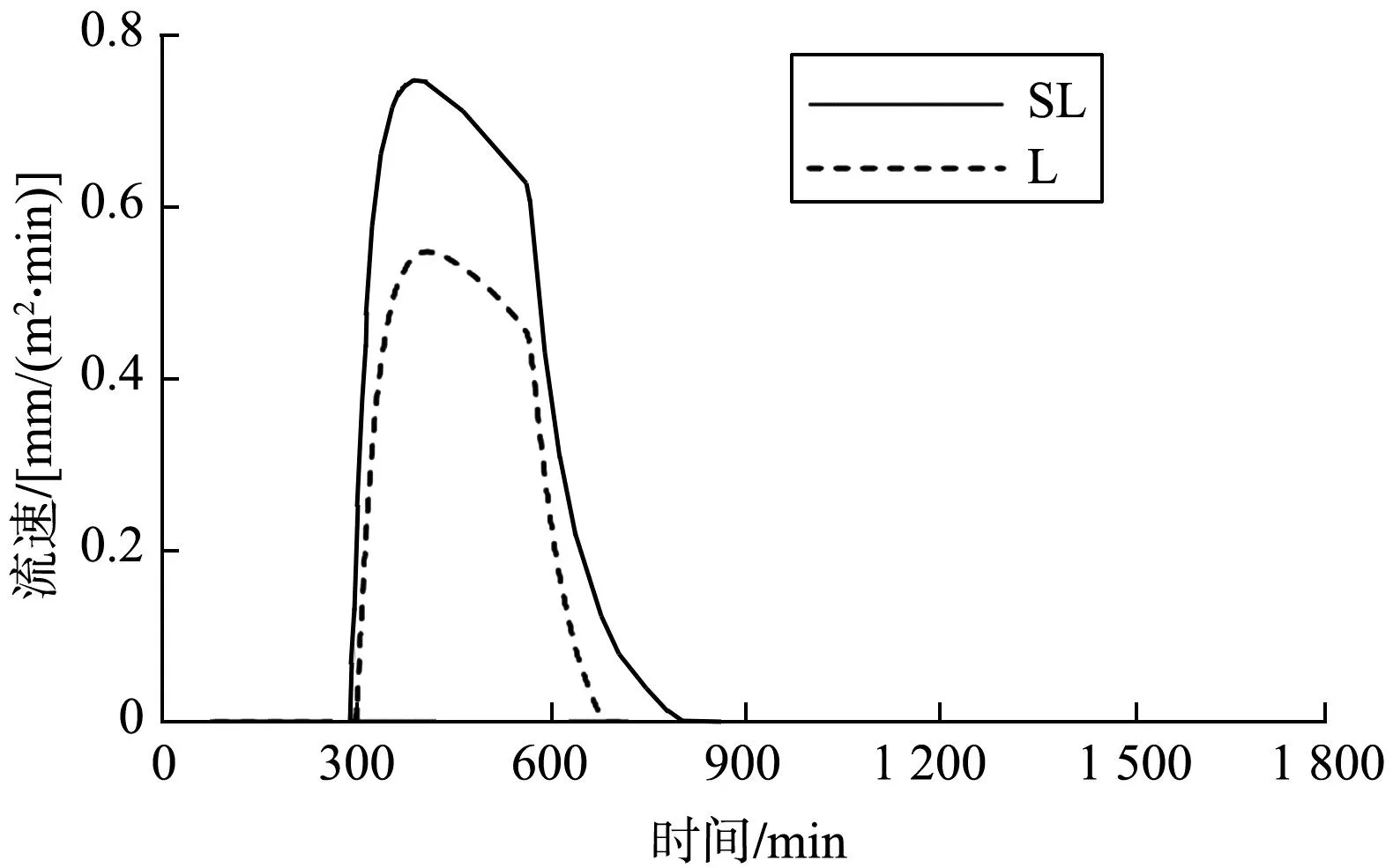
图2 设施穿孔管产流曲线

由图2可看出:相比于降雨径流,这两种原位土设施的穿孔管产流开始时刻延长了295～300 min,产流结束时刻延长了320～445 min,产流峰值消减了53.72%～66.94%。由此可见,当雨水径流通过设施填料的渗透过程,可将雨水径流暂时储存后再缓慢释放,具有显著的延时、消峰作用。设施产流开始时刻为L>SL,产流峰值和产流结束时刻为SL>L。由此可见,原位土类型对穿管产流影响显著,即随着原位土渗透系数增加,穿孔管开始产流时刻延长,产流峰值降低,产流结束时刻提前。

2.3 原位土对设施外渗的影响

在一年一遇6 h降雨作用下,4种原位土类型设施的侧向和底部单位面积累计外渗水量如图3。

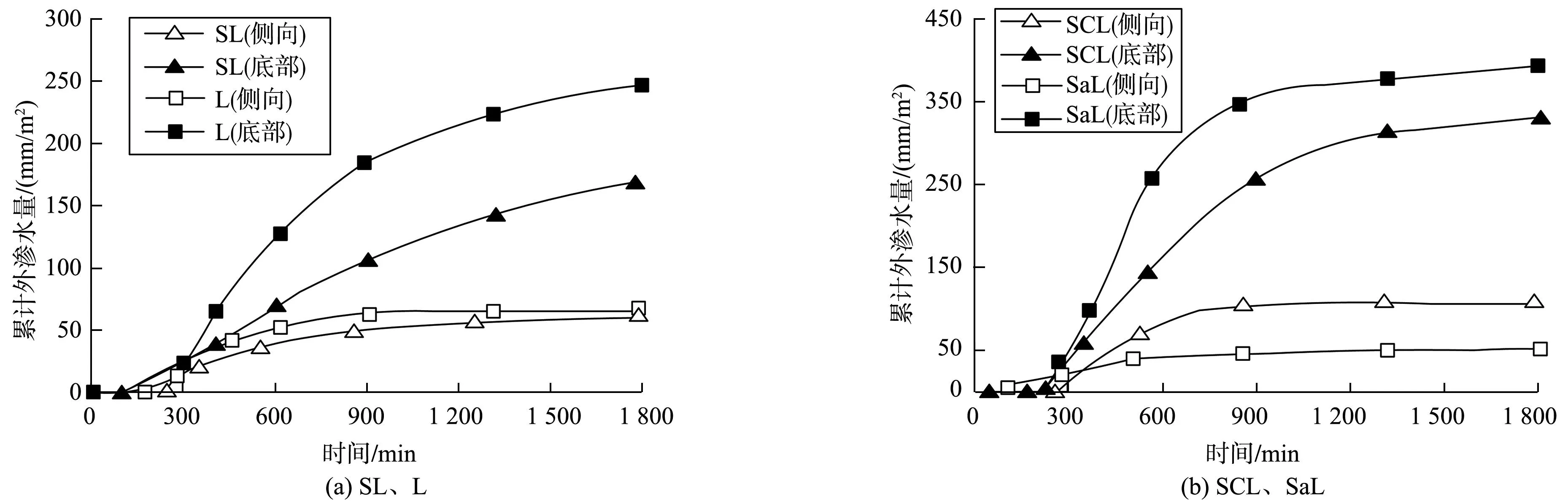
图3 4种原位土类型设施单位面积累计外渗水量

由图3可知:随着时间增加,设施的外渗水量逐渐增加并趋于稳定,随着原位土渗透系数增加,外渗达到稳定的时间相应提前。降雨结束后的24 h,这4种原位土类型设施的底部和侧向单位面积外渗水量分别为168.11～396.10、 50.60～110.31 mm/m2,底部外渗水量是侧向的2.78～7.82倍,这说明设施的水分外渗基本以底部为主。对于底部外渗而言,这4种原位土类型设施累积外渗水量为SaL>SCL>L>SL,即随着原位土渗透系数增大,设施的底部外渗水量也随之增大。对于侧向外渗而言,这4种原位土类型设施的累积外渗水量为SCL>L>SL>SaL。整体而言,原位土类型对设施的侧向外渗影响较弱,当原位土为SCL时,设施的侧向外渗水量相对较大,约为另外3种的2倍,这主要是SCL的渗透系数相比种植土小很多,且设施未设置穿孔排水管,水分易在设施底部累积,从而增加了侧向外渗水量。

2.4 原位土对设施径流调控效应的影响

在一年一遇6 h降雨作用下,这4种原位土类型设施的径流调控效果如图4。

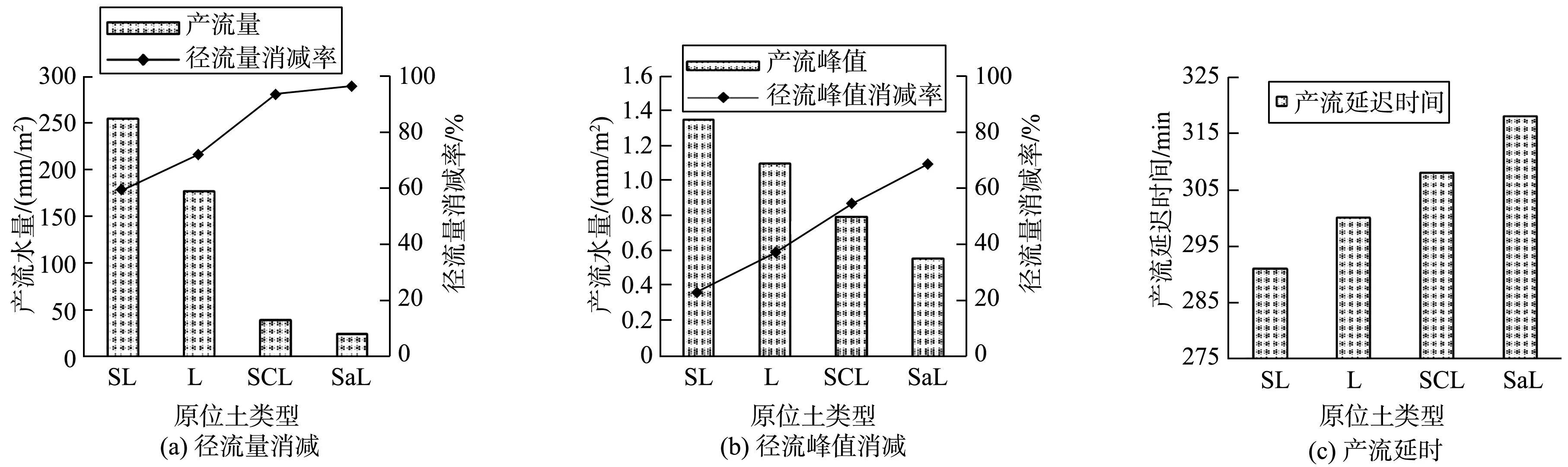
图4 4种原位土情况下生物滞留设施径流调控效应

由图4可知:4种原位土类型设施的产流量和径流量消减率范围分别为23.85～254.90、 59.27%～ 96.19%,产流峰值和径流峰值消减率范围分别为0.55～1.42 mm/(m2·min)和18.43%～68.08%,产流延迟时间为291～318 min。这4种原位土类型设施的径流量消减率、径流峰值消减率、产流延时为SaL>SCL>L>SL,即随着原位土渗透系数增大,设施的径流量消减率、径流峰值消减、产流延时均随之增大,设施对降雨的径流调控效果增强。此外,与径流峰值消减率及产流延时相比,穿孔排水管设置对径流量消减率的影响更为显著,当设施未设置穿孔排水管时(如SaL、SCL),大部分雨水径流可渗入地下,导致设施的产流量显著减小。

3 结 论

笔者采用VADOSE/W模型对生物滞留设施及原位土在单一降雨事件下的水分运移过程进行了模拟,分析了原位土类型对设施的表层积水、穿孔管产流、水分外渗及径流调控效应的影响特性,得出如下结论:

1)当配置了穿孔排水管,原位土类型对设施的表层积水过程影响甚微;当未配置,且原位土渗透系数相比设施填料层小许多时,易加剧设施溢流风险;

2)随着原位土渗透系数增加,设施的穿孔排水管产流时刻延长,产流峰值降低,产流结束时刻提前;

3)设施的水分外渗以底部为主,且随着原位土渗透系数增大,设施的底部外渗水量也随之增大,而侧向外渗受到的影响较小;

4)设施的径流调控效果受原位土影响显著,随着原位土渗透系数增大,设施的径流量消减率、径流峰值消减和产流延迟时间均随之增大。

在进行生物滞留设施设计及布局时,应充分考虑不同地区原位土的差异,以保证设施满足相应的径流控制目标。特别是当原位土渗透系数相比设施的填料层较小时,在连续降雨作用下,设施可能发生冒顶,影响其正常功能,此时应考虑设置穿孔排水管。