改进的水封石油洞库群渗水量预估研究

张继勋 杨 帆 杨 玲 任旭华

(1. 河海大学 水利水电学院， 南京 210098; 2. 浙江省宁海县水利局， 浙江 宁海 315600)

改进的水封石油洞库群渗水量预估研究

张继勋1杨 帆1杨 玲2任旭华1

(1. 河海大学 水利水电学院， 南京 210098; 2. 浙江省宁海县水利局， 浙江 宁海 315600)

基于圆形隧洞断面的渗水量经验公式，结合地下洞室群的实际情况，考虑洞库间距的相互影响，对公式进行了修正，得到了考虑地下洞室群相互影响的水封石油洞库渗水量计算公式．对比数值计算、经验公式和现场实测结果，改进公式算出的渗水量与模拟及现场实测数据较为吻合，说明该修正的渗水量估算公式更加合理，可在水封洞库的渗水量的计算中推广应用．

水封石油洞库； 渗水量； 洞库间距； 大岛洋志公式

水封石油洞库是指在洞库上方设置水幕，保持地下水位稳定，在洞库周围形成指向洞库的渗流，实现石油的完全密封．水封洞库既要让地下水渗入洞库周围，使洞库周边水压大于同高度油品压力[1]，又不能无限制地渗入，污染油品，增加洞库运行成本．因此进行洞库涌水量的预估很有必要，对围岩裂隙防渗及封堵处理也有着重要意义[2]．

20世纪90年代早期，随着我国山东黄岛[3]和浙江象山地下水封油库建成投入使用[4]，一些学者基于我国地下水封洞库实际工程，围绕地下水封洞库围岩渗流场、洞库渗水量和油品渗漏问题进行了相关模型试验研究和理论分析[5]，其中国外有代表性的是S. Finsterle[6]和Hajime Yamamoto以及Karsten Pruess，分别模拟了渗水过程并预测了渗水量的计算方法，国内有代表性的是清华大学的崔京浩[7]教授，提出了地下水封洞库渗水量估算的理论公式．

地下水封石油洞库地质条件复杂[8]，且属于洞库群，采用精确解预测渗水量比较困难，也有较大误差[9]．但是采用一些简化方法：①介质均匀且渗透性各项同性；②渗流稳定；③把洞室近似为圆形洞室，且洞室顶部的水头保持不变时，可以采用解析公式近似预测渗入洞库的渗水量的大小[10]．对于地下水封洞库来说，当洞库埋深较大时，洞库没有穿越较大的断层，近似满足上述条件．但经验解析公式只适用于单个洞库渗水量计算，未考虑水封石油洞库群的洞库间距对渗水量的影响．本文对经验公式的修正参数进行了改进，对某水封石油洞库群渗水量进行数值模拟，对比计算结果与模拟结果和现场实测数据，对改进公式的合理性开展了讨论．

1 大岛洋志公式

1.1 公式原理和问题

20世纪60年代，Goodman研究了圆形隧洞渗水量的计算问题，如图1所示．假定隧洞周边水头为恒定值h1．

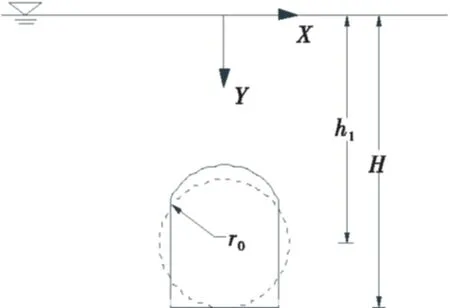
图1 圆形隧洞渗水量计算模型

根据Polubarinova-Kochina提出的深埋隧洞水头和隧洞位置的关系[11]，可知：

(1)

在隧洞周围有x2+(y-h1)2=r2.

对于深埋隧洞，h1≫r时，上式可近似写成

取60只小鼠，随机分为正常对照组（10只）和造模组（50只）。造模组小鼠一次性腹腔注射降植烷0.5 mL，正常对照组小鼠同法给予等体积生理盐水。注射前及注射后2、3、4、5、6个月时，采用ELISA法检测小鼠血清中抗ds-DNA抗体；注射前及注射后每月1次采用目测尿蛋白试纸检测小鼠尿蛋白。结果，造模组小鼠注射降植烷2个月后，其抗ds-DNA抗体水平显著高于正常对照组（P＜0.05或P＜0.01），且在6个月内该抗体水平逐渐升高；第6个月时，90%的造模组小鼠尿蛋白呈强阳性（++++），提示典型狼疮病变形成。

(2)

根据达西定律，可得v=-2Kc/r．因此，隧洞周围的渗水量q=-2πrv=4πKc，将c回代式(2)，变形后可得地下水封洞库渗水量的计算近似公式为

(3)

其中，H是地下水至水封洞库底板的距离；r0是洞库转化为圆形截面的近似半径；d是洞库转化为圆形截面的近似直径．后来大岛洋志在Goodman公式的基础上又做了一些修正，加了修正系数m，就是现在通常用到的大岛洋志经验公式

(4)

m通常取0.86．

根据推导过程，大岛洋志公式假定洞库周边的围岩为均匀各项同性介质[12]，且只考虑单个隧洞，因而适用于单个洞库渗水量的计算，是基于单个洞室的理论解．对于单个洞库来讲，除了洞库水文地质条件以外，渗水量只受洞库形状面积，地下水位至洞库顶部距离的影响，而对于洞库群，除了上述两个因素，洞库渗水量还受相邻洞库间距的影响[13]，洞库间距越大，相邻洞室对其的约束就越小[14]，如图2所示，R为洞库相互影响半径．

图2 相邻洞室对中间洞室渗水量的影响示意图

1.2 改进公式

根据公式存在的问题推行修正公式，考虑左右相邻洞室对洞库的影响，用数据拟合方法对公式进行修正．建立5个模型进行渗水量分析，每个模型设5个洞库，每个模型的洞库间距分别为20、30、40、50、60 m，地下水位至洞库顶部的距离分别取100、120、140、160 m，渗透系数为1×10-4m/d ．数值模拟自然水位下洞库渗水量见表1．

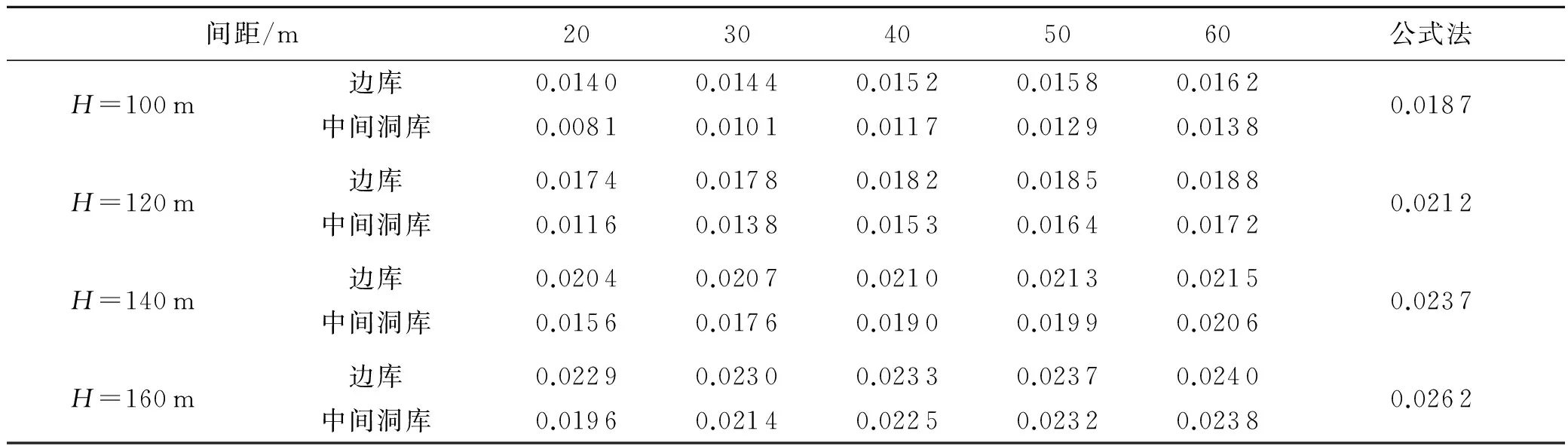
表1 不同间距洞库渗水量(单位：m3/d)

由表中数据可知，对于边库，由于洞库一边处于半无限长弹性体，所以受相邻洞室影响不大；而中间洞库受相邻洞室影响较大．经验公式与数值模拟得到的渗水量差距较大，误差值最低也有5%，最大达60%．当地下水位至洞库底板距离越小，误差越大；相邻洞库间距越大，渗水量越大．因此，对于m的修正应当考虑洞库的间距L的影响．

根据表1中数据进行数据拟合，对比数值模拟和计算公式的渗水量，将计算公式的数值修正到数值模拟值，修正过程中考虑L对m的影响，每次修正得到不同L和H下的m值，得到m对H和L的关系曲线以及对应方程，调整之后，得到修正公式如下：

图3 洞库示意图

2 工程实例

我国某地下水封石油洞库工程，储库洞室区呈北偏西5°方向展布，东西宽约600 m，南北长约838 m，主要包括2条施工巷道、9个主洞室、6个竖井及5条水幕巷道．9个主洞室平行设置，每3个主洞室之间通过4条支洞相连组成一个罐体，共分为3个洞罐组．主洞室设计底面标高为-50 m，长度为484～717 m不等，设计洞跨20 m，洞高30 m，截面形状为直墙圆拱形．两个相邻主洞室之间设计净间距为30 m．主洞室顶面以上25 m设置5条水平水幕巷道，垂直主洞室方向布置．各个主洞室的左右间距见表2．

表2 各个洞室的左右边距(单位：m)

2.1 计算模型与参数

选取工程地表高程较低，地下水埋深较浅的典型断面，将模型简化为二维平面模型，不考虑施工洞．考虑到洞室的开挖产生的降水漏斗影响范围较大，同时为了减少模型左右水头边界条件对结果合理性的影响，模型的左右方向计算范围从洞室外边缘向外延伸1 000 m，底部范围从洞室地面向下延伸400 m，顶部至山体表面．网格剖分为四边形单元，共划分了47 607个单元，47 669个节点，洞室周边网格加密．模型边界条件是左右边界横向位移为0，底部边界横向、纵向位移均为0，其他为自由位移边界．模型底部及左右边界设为已知水头边界，上方为流量边界，考虑降雨入渗．地区降雨入渗系数为0.073，洞库设计地下水位标高至洞室顶部50 m，水幕巷道布置在主洞室顶面以上25 m处，每间隔10 m布置水幕钻孔，注水压力0.1～0.6 MPa，取0.3 MPa计算．围岩渗透系数为1×10-4m/d，弹性模量取17.1 GPa，泊松比取0.21．断面布置如图4所示，具体布置及网格剖分情况如图5所示．

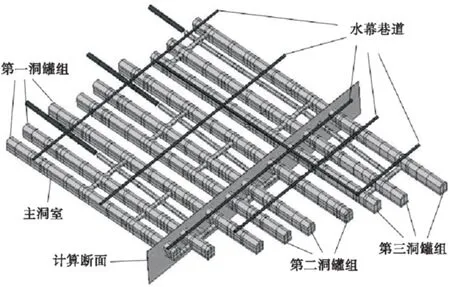
图4 典型断面布置图

图5 计算模型及网格

2.2 计算成果

根据实测数据，该工程某年枯水期地下水位为126 m，测得1号、4号、6号、7号洞库流量分别为0.019 5 m3/d、0.014 6 m3/d、0.016 3 m3/d、0.014 5 m3/d，丰水期地下水位为169 m，测得1号、4号、6号、7号洞库流量分别为0.026 1 m3/d、0.022 8 m3/d、0.024 2 m3/d、0.023 1 m3/d．根据表2，其1号洞为边库，4号和7号洞为洞库间距较小的中间洞库，6号洞为洞库间距较大的中间洞库，这4个典型洞库很好地涵盖了洞库间距的所有情形，本文在实测数据点和工况相对较少的情况下，着重选取这4个洞库讨论研究．

其中：q0为洞身通过含水体的单位长度可能最大渗水量；k为渗透系数，取1×10-4m/d；H为含水层中原始静止水位至地下工程底板距离；r0为洞室横截面等效圆半径，取13.48m；d为洞室横断面等效圆直径，取26.96m．

表3 数值模拟下不同水位各洞库流量 (单位：m3/d)

表4 大岛洋志公式计算下不同水位各洞库流量 (单位：m3/d)

表5 修正公式计算下不同水位下各洞库流量 (单位：m3/d)

2.3 成果分析

由实测数据可以看出，不同水位下1号、4号、6号、7号洞库的渗水量并不相同，只有1号边库的渗水量和大岛洋志公式算出的结果近似，而6号、7号中间洞库受到相邻洞库的影响，洞室周围水力梯度要小得多，渗水量偏小．结合表2可以看出，相邻洞库间距越大，渗水量越大．表3数值模拟的结果也符合上述规律，进一步验证了大岛洋志公式是基于单个洞室的理论解，没有考虑相邻洞室的相互影响[15]．而修正公式计算值与模拟值和实测值之间差距相对较小．

鉴于实测数据点和工况相对较少，本文只是选取部分数据，将数值计算得出的渗水量，经验公式算出的渗水量和修正公式得到的渗水量对比，如图6～9所示．

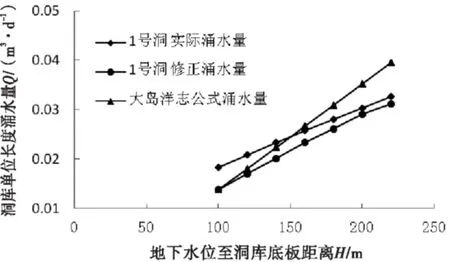
图6 1号洞修正流量对比图

结合图表可以看出，考虑了洞库间距后，修正公式各计算数据与模拟数据相差均在±5%以内，均比原经验公式计算值更符合实际情况．

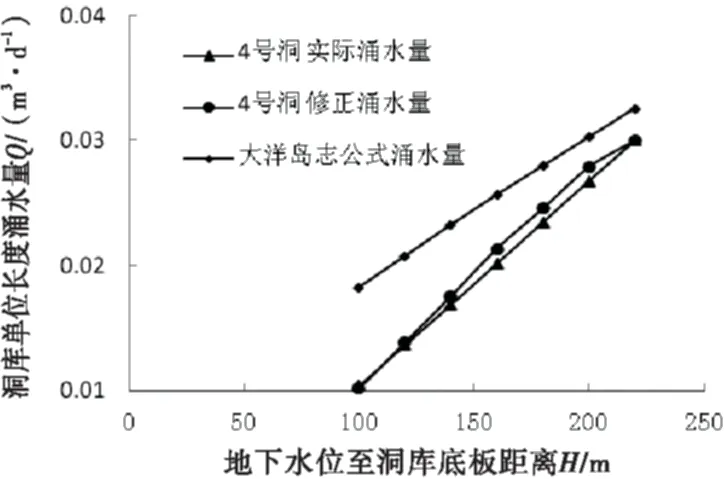
图7 4号洞修正流量对比图

图8 6号洞修正流量对比图

图9 7号洞修正流量对比图

3 结 论

本文根据工程实测数据，利用大型通用程序ABAQUS对大岛洋志公式进行试算验证，进而对公式修正验算．主要结论如下：

1)大岛洋志公式是基于单个洞室的理论解，适用于单个洞库渗水量的计算．在用于洞室群的渗水量估算时，应对经验公式进行修正．

2)水封石油洞库各洞库渗水量各不相同，中间洞库的渗水量，受到相邻洞库的影响，渗水量偏小，且相邻洞库间距越大，渗水量越大，说明渗水量预估研究应当考虑洞库间距．

3)基于修正公式的水封石油洞库群渗水量的计算，考虑了洞库间距对渗水量的影响，计算精度相对于传统公式均有提高．可在多洞室洞库群的渗水量计算研究中推广应用．

[1] 严冬青，任旭华，张继勋，等．水幕参数对地下水封石油洞库的涌水量影响分析[J]．三峡大学学报(自然科学版)，2014，36(1)：15-18．

[2] Kyung-Ho Park,Adisorn Owatsiriwong, Joo-Gong Lee． Analytical Solution for Steady-state Groundwater Inflow Into a Drained Circular Tunnel in a Semi-infinite Aquifer：A Revisit [J]． Tunnelling and Underground Space Technology, 2008,23(2)：206-209．

[3] 时洪斌．黄岛.地下水封洞库水封条件和围岩稳定性分析与评价[D]．北京：北京交通大学,2010．

[4] 王者超，张振杰，李术才，等．基于离散裂隙网络法的地下石油洞库洞室间水封性评价[J]．山东大学学报,2016,46(2)：94-100．

[5] 黎照洪，胡 成，陈 刚，等．基于离散裂隙网络的烟台水封洞库渗水点分析[J]．安全与环境工程,2016,23(5)：170-173．

[6] Finsterle S, Ahlers C F, Trautz R C, et al． Inverse and Predictive Modeling of Seepage Into Underground Openings [J]． Journal of Contaminant Hydrology, 2003, 62-63(1)：89-109．

[7] 郭书太．地下储油库工程中地下水的利用和处理[J]． 工程勘察, 2008(S1)：217 - 220．

[8] 王者超，李术才，梁建毅，等．地下水封石油洞库渗水量预测与统计[J]．岩土工程学报,2014,36(8)：1490-1497．

[9] Dimitrios Kolymbas, Peter Wagner． Groundwater Ingress to Tunnels - The Exact Analytical Solution [J]． Tunnelling and Underground Space Technology 2007,22(1)：23-27．

[10] Jin-Hung Hwang, Chih-Chieh Lu． A Semi-analytical Method for Analyzing the Tunnel Water Inflow [J]． Tunnelling and Underground Space Technology, 2007,22(1)：39-46．

[11] 王振宇，陈银鲁，刘国华，等．隧道涌水量预测方法计算研究[J]．水利水电技术, 2009,40(7)：41-44．

[12] 吴治生．不同地质边界条件岩溶隧道涌水量预测及展望[J]．铁道工程学报,2007(11)：48-55．

[13] 丁万涛，李术才，徐帮树，等．隧道涌水量解析公式在海底隧道工程中的应用[J]． 地下空间与工程学报,2008,4(4)：662-664．

[14] Wing Kei Kong． Water Ingress Assessment for Rock Tunnels：A Tool for Risk Planning[J]． Rock Mech Rock Eng, 2011,44(6)：755-765．

[15] 许建聪，郭书太．地下水封油库围岩地下水渗流量计算[J]． 岩土力学, 2010,31(4)：1295-1302．

[责任编辑 王康平]

Improved Water Seepage Prediction in Seal Petroleum Cavern Group

Zhang Jixun1Yang Fan1Yang Ling2Ren Xuhua1

(1. College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China; 2. Ninghai Water Conservancy Bureau in Zhejiang Province, Ninghai 315600, China)

Based on water seepage empirical equation of circular cross-section tunnel, the paper combines the practical situation of underground cavern group and consideres the interplay of cavern spacing to improve the formula, and then get an improved formula. Comparing the results of numeric calculation, empirical equation and field measuring, it is shown that the improved formula's results are closer to the results of simulation and field measuring, so as to show that the improved water seepage estimation formula is more reasonable and can be popularized and applied to water seepage calculation of seal petroleum caverns.

seal petroleum cavern; water seepage; cavern spacing; Hirishi Oshima empirical equation

2016-12-05

国家科技支撑计划“南水北调中东线工程运行管理关键技术及应用”(2015BAB07B00)

张继勋(1974-)，男，副教授，博士，研究方向为水工结构．E-mail：zhangjixun@hhu.edu.cn

10.13393/j.cnki.issn.1672-948X.2017.02.004

TV314

A

1672-948X(2017)02-0014-05