基于增强支持向量机的电力隧道多状态全过程监控方法
刘滨,刘春,邵必飞,杨郭明,苟军,黄贵武
(国网兰州供电公司,甘肃 兰州 730030)
随着社会的进步,电力与人们的生活日渐密切,电缆作为一种传输装置,被用于电力及其信号的传送,因此对于电缆的保护是十分必要的,而电力隧道的作用就在于此,它可以将设置在支架上的众多电缆容纳其中,能较好地保护电缆,使电力传输能够正常运行[1-3]。但受到自然因素及其他因素的影响,电力隧道内会出现一些异常的情况,如电缆导体温度过高、护层电流异常、积水过多、有异物入侵以及围岩发生变化等。为了能够尽早地发现异常现象,使损失降到最低,就需要对电力隧道多种状态进行全过程的监控[4-5]。
文献[6]针对电缆隧道内积水的问题,提出了一种改进的基于区域建议的卷积神经网络(Faster R-CNN)方法,并利用其进行电缆隧道积水定位识别,利用支持向量机(SVM)进行图像分类,增强分类的置信度,使用区域建议网络(RPN)提取隧道积水原图中的区域建议,然后用Fast R-CNN检测网络在建议框中进行图像识别、SVM分类和位置精修。文献[7]针对电力隧道运维存在着信息化水平低、防灾害能力弱、运维成本高和缺乏统一技术标准的问题,建立了电力隧道在线监控和智能巡检模式,运行人员可实时监测隧道温湿度、水位、有毒有害气体等核心运行数据。上述方法虽然对电力隧道异常状态起到了一定的检测作用,但是在检测的效率、准确率上表现略有不足。
支持向量机可以处理高维、小样本及非线性特征的问题,不需要依赖整个数据,而且有较强的泛化能力。因此本文提出的基于增强支持向量机的电力隧道多状态全过程监控方法,是在对支持向量机增强后,又对其参变量求优,从而更加准确地对电力隧道多种状态的全过程进行监控。
1 电力隧道多状态全过程监控方法
1.1 电力隧道多状态描述
电力隧道状态的监控就是根据其运转的状态是否正常来进行判断,是一个动态的过程。电力隧道运行状态模式通常分成正常和异常状态两种模式,其中异常状态又可划分为上升趋势状态、下降趋势状态、向上阶跃状态与向下阶跃状态。如果电力隧道存在异常因素,那么通过电缆隧道状态智能监测系统获取的电力隧道状态的实测动态数据流就会发生变化,反映出不同的变化特征,从而说明此时电力隧道处于非正常状态。
由于通常情况下电力隧道都为正常运行状态,且状态特性观测数据近似正态排列,这样大量的异常状态数据就不容易被获取,因此可运用Monte Carlo(蒙特卡罗)方法模拟电力隧道多状态模式数据[9],其函数可以描述为:
S(t)=Y(t)×σ+O(t)+M,t=1,2,…,L
(1)
式中,处于时间点t的电力隧道多状态特性实测数值用S(t)描述,设计目标数值用M描述,电力隧道运行过程中因偶然性因素而产生的随机波动用Y(t)描述,因异常性因素产生的波动用O(t)描述,平稳时候的标准差用σ描述,电力隧道动态数据流的大小用L描述。
1.2 电力隧道多状态特征混合
为了准确地提取电力隧道多状态混合特征,可以对电力隧道动态数据流S(t)进行分解与重组,这一过程可通过一维离散小波分解来实现[10,11]。
一维离散小波分解可以把电力隧道动态数据流分化成低频近似与高频细节两个部分,并运用高通与低通滤波器来完成分解,设定P0S=S,层级为j的小波分解可以描述成:
Pj-1S=QjS+PjS=
(2)
式中:趋势变化斜率用a描述,Pj、Qj表示低高频分解,它们的因数分别用cFj和cMj描述,j=1,2,…,G,a=0,1,…,L/2j-1。S(t)的大小用L描述,分解层的数量用G描述,小波函数ψ(t)的系数用ψja描述,尺度函数φ(t)的系数用φja描述。如果小波分解在G层完成,那么S(t)的“噪声”则大部分会保留在cMj里,而低频近似部分则会保留大量的有价值信息,cFj与cMj用公式描述为:
(3)
(4)
式中,高通滤波器用w(v)描述,低通滤波器用g(v)描述。根据式(3)可以获取层级是G的低频近似因数cFG,并将其作为电力隧道状态的主要特征,然后通过cFG与每个层级的cMj,对电力隧道动态数据流S(t)实行一维离散小波重组,数据序列重组后描述为:
(5)
要想使各类状态之间的细节信息区分得更加细致,并且使电力隧道状态特征数据的维度降到最低,那么可以运用仿真实验再次筛选出3类形状特征,即BRANGE、REAE、ABDPE。在重组数据序列Sc(t)中对这3类特征进行提取,分别用BRANGEc、REAEc、ABDPEc描述。
(1)将Sc(t)平均划分成固定的4段,可得出BRANGEc特征与REAEc特征,函数可以描述为:
BRANGEc=max(qur)-min(qur)
(6)
(7)
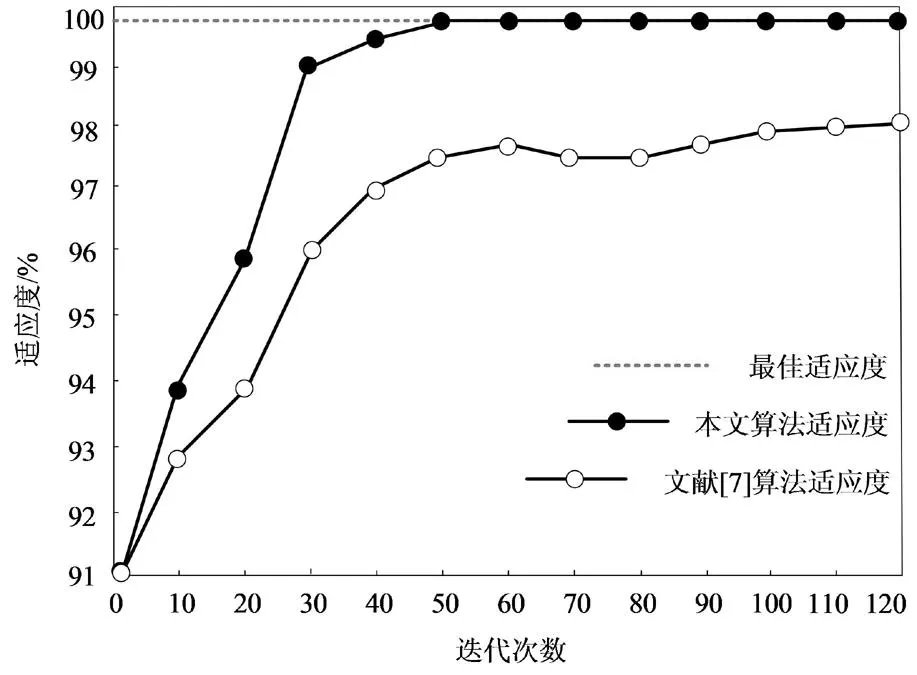
式中,u=1,2,3,r=2,3,4,u (2)将Sc(t)划分成不固定的2段,可得出ABDPEc特征,而分划点的位置是当2段中数据序列最小二乘估计的合并均方误差的值最小时所在的区域,其函数可以描述为: (8) 式中,整体与分割后数据序列的最小二乘拟合直线的斜率分别用Al和A描述。 按顺序对特征实行组合操作,也就是将已获取的BRANGEc、REAEc、ABDPEc特征分别添加至每种电力隧道运行状态模式提取出的低频近似系数特征向量cFG的后面,从而获取到电力隧道多状态混合特征向量D,描述为: D=[cFGRANGEcREAEcABDPEc]T (9) 1.3.1 增强支持向量机 将电力隧道运行异常状态的检测转化成非线性、小样本、多种类的分类问题,可通过支持向量机(SVM)来解决。 (1)支持向量机 支持向量机利用分类平面来处理有关二分类的问题,而该平面则需要能使二种数据最小距离最大化[12,13]。 设定支持向量机的数据样本用{xi,yi},i=1,2,…,n,xi∈Rn,yi∈{+1,-1}描述,输入是xi,目标输出是yi。支持向量机经过数据样本学习,可以得到一个分类平面,这个平面可以将数据分为两类,描述为: f(x)=ωδ(x)+b (10) 式中,权向量用ω描述,且ω∈Z,δ:Rn→Z,偏置向量用b描述,δ(x)表示数据样本分布,另外,如果其中一类数据每个数据点都分布于超平面一边,那么: ωδ(xi)+b≥yi (11) 设定二种数据间隔用d来描述,根据SVM几何定义得出,d=2/‖o‖,‖o‖是欧几里得范数,那么可将分类问题变成优化问题来处理: (12) 如果出现线性不可分的情形,那么就可以引进松弛变量ζ来减少对超平面的要求,另外还需要添加惩罚参数C来惩罚由于错误分类产生的损失,由此可将式(16)调整为: (13) 将拉格朗日乘子引入上面的优化问题并进行求解,获取SVM最优超平面分类函数为: (14) 核函数采用的是高斯核函数,描述为: k(xi,x)=exp(-‖xi-x‖/2g2) (15) 式中,g是核函数半径参数。 电力隧道多状态的多类问题,可以通过构建多个两类支持向量机,运用一对多的方式来处理,另外对于H类分类问题,分类超平面的数量也应为H。 (2)访问策略 对下一步要访问的点进行选取,也就是选取访问与H个超平面最近的点x′,描述为: x′=argmin|fi(x′)|,i=1,2,…,h (16) (3)标记新点类别与更新分类器 运用现有的SVM分类器对x′进行分类,设定运行至第h类,获取的分类结果为“对”“错”两种。若分类结果为“对”,那么h标记为x′的类别,同时在第h类里添加x′,对第h类支持向量机进行再次训练,从而获取新的第h个分类超平面。若分类结果为“错”,那么可分为以下两种情况: 情况1:当fh(x′)<0时,依据从小至大的顺序对x′与H个超平面的间距进行设置,同时调整x′至与其相应的类别里,该类别应归属于与x′较近的超平面,直至正确,从而得到更新后的标记点,同时把该点添入正确类别E的训练集内,进而更新超平面E。 情况2:当fh(x′)>0时,依据从小至大的顺序对x′与其他H-1个超平面的间距进行设置,剩下步骤按情况1操作,最后得到更新的超平面E和h。 如果持续N次对待标记电力隧道多状态样本分类结果均是正确时,那么就可终止更新样本集与分类器。此时N越大,则说明访问的点越多,输出结果的准确率就越高。 1.3.2 PSO参数求优 设置PSO中的粒子分别是SVM的惩罚参数C与核函数半径参数g,其适应度选取的是SVM分类正确率[14,15],描述为: W=识别正确数目/(识别正确数目+识别错误数目) (17) 更新粒子的速度与位置,描述为: (18) 1.3.3 电力隧道多状态识别 基于PSO-SVM电力隧道多状态识别模型,见图1。 以某地区的电力隧道为实验对象,该电力隧道全长约1.5 km,通过顶管施工技术,将直径为2.7 m的水泥管道置于约20 m深的地下。 为了衡量本文方法提出的增强支持向量机的分类性能,与文献[6]方法进行对比实验,选取存储于UCI数据库中该电力隧道的部分数据进行了分类检测。设定分类结果持续正确的点数量用N描述,访问的点数量用J描述,样本类别的数量用M描述,且M=3,分类结果正确的次数(实际实验次数)用T描述,计划实验次数用Ω描述,且Ω=2M2J,利用本文方法得出的测试结果如表1所示。 图1 基于PSO-SVM的电力隧道多状态识别模型 表1 本文方法增强支持向量机的分类效果 由表1所知,利用本文方法访问较少数量的点,即可达到较高的准确率,当访问4个点时,准确率已达90%以上;访问7个点时,准确率已接近100%。从实验次数来看,当M=5,计划实验次数分别为36、90、144、234、378、450、558,而实际实验次数则分别为7、16、27、39、51、63、78,实际实验次数远低于计划实验次数,而文献[6]方法计划实验次数均高于本文方法,且准确率较低,由此可见,利用本文方法增强的支持向量机具有较好的分类效果。 表2 文献[6]方法增强支持向量机的分类效果 为了验证本文方法的性能,实验设定种群数量为12,惩罚参数取值为[0,10],核函数取值为[0,10],最大迭代次数是120,与文献[7]方法进行对比测试,得到的粒子群优化适应度走势图,见图2。 图2 粒子群优化适应度走势图 由图2可知,本文方法明显优于文献[7]方法,随着迭代代数的增加,适应度快速接近最佳适应度水平,迭代次数为30次时,适应度达到99%左右,当迭代次数为50次时,已完全达到最佳适应度标准并收敛。由此说明,通过PSO寻找最佳参数速度快、适应度高,进而验证本文方法性能好。 为了验证本文方法对于电力隧道多状态全过程监控的有效性,实验对该电力隧道中01-05号电缆的导体温度进行了监控。正常情况下,电缆导体最高额定工作温度为90℃,短时间过载温度不能高于130℃,短路时最高温度不能高于250℃时且持续时间不能超过5 s。利用本文方法得到的监测结果,如图3所示。 图3 电力隧道多状态全过程监控结果 由图3所知,截至当日20时,01-03号电缆的导体温度均在60℃-70℃之间浮动,在允许的范围之内,属于正常状态。04号电缆在0时至18时的导体温度处于正常范围,但是在20时,导体温度则迅速上升至118.27℃,出现了向上阶跃的态势,另外对比昨日同期数据,昨日此时04号电缆的导体温度也超过了正常工作温度,达到115.39℃,属于异常状态,提示报警信息为1级。05号电缆在18时导体温度已达90℃左右,之后快速阶跃至127.35℃,接近短时间最高过载温度,应立即给予处理,提示报警信息为2级。由此可见,利用本文方法对电力隧道内电缆导体温度做到了实时监控,对出现的正常状态、异常阶跃状态都能及时、准确地反映出来,并给出相应的预警信息,说明本文方法对电力隧道多状态全过程的监控有效且准确。 为了进一步呈现本文方法的应用性,实验对该电力隧道内湿度情况进行了实时监控,得到的结果如图4所示。 图4 电力隧道内湿度情况监控结果 由图4可知,运用本文方法可以有效地对电力隧道内湿度情况进行监控,得出的监控结果为湿度呈上升趋势,并提示存在低级风险,建议除湿处理,由此可见,本文方法具有较强的应用性。 为了及时掌握电力隧道运行状态,保证电力的正常供应,提出了一种基于增强支持向量机的电力隧道多状态全过程监控的方法。该方法利用粒子群优化算法对增强后的支持向量机进行优化,以达到较好的分类效果,进而实现电力隧道多状态全过程监控方法。通过实验证该方法能有效、准确地监控电力隧道多状态的全过程,具有较好的应用性。1.3 电力隧道多状态混合特征的PSO-SVM识别方法
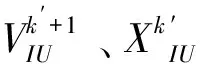
2 实验分析





3 结 论

