复杂卸荷条件下杭州淤泥质黏土的力学特性试验研究

曹宇春,王换成,王 羿,蔡 越,祁 迪

(1.浙江科技学院 土木与建筑工程学院,杭州 310023;2.浙江明思特建筑支护技术有限公司,杭州 311022;3.杭州鑫高科技有限公司,杭州 311107)

随着中国地下空间开发进程的不断推进,越来越多的工程项目涉及基坑与基坑、基坑与隧道或隧道与隧道相互交叠或近邻的情况。基坑与隧道施工均涉及土体开挖,进而引起卸荷,且由于相互交叠或近邻现象,在施工及运营期引起岩土体产生复杂的卸荷与加荷现象。与常规的水平或竖向单向卸荷不同,复杂卸荷常涉及水平向和竖向同时卸荷的情况。由于应力路径及土体弹塑性的影响,卸荷后再加荷与常规连续加荷条件下岩土体的强度与变形特性存在差异。

为了更好地指导设计与施工,一些研究者在土体卸荷力学特性方面开展了试验研究。刘国彬等[1-2]对上海3种软黏土进行了K0固结室内应力路径试验,发现卸荷对土体的模量有明显影响,同时卸荷应力-应变关系曲线可以用方程进行归一化处理。宰金珉等[3]通过对原状黏性土进行的竖向加荷和水平卸荷的三轴试验,发现卸荷模量要大于加荷模量,但有效抗剪强度指标基本保持一致。郑刚等[4-5]对天津粉质黏土进行了三轴剪切试验,发现卸荷总应力强度指标比常规试验结果更大,而有效应力抗剪强度参数基本上一致。Yuan等[6]对重塑黏土进行了两类轴向压缩及轴向拉伸三轴试验,研究表明:卸荷条件下的内摩擦角和剪切模量大于加载条件下的数值;拉伸屈服强度明显小于压缩屈服强度,且这种差异随围压的增加而增大。张坤勇等[7]针对粉质黏土开展了K0固结排水卸荷三轴试验,发现土的抗剪强度参数受加卸荷过程和应力路径影响不大。Huang等[8]通过粉质黏土的卸荷三轴试验研究发现随着卸荷比的增加,初始切线模量先减小后增加,黏聚力会逐渐减小而内摩擦角变化不大。汪中卫[9]通过常规和水平向三轴实验卸荷研究了应力路径对黏性土力学性质的影响,发现水平向卸荷三轴试验应力-应变关系具有明显的非线性,与常规三轴试验有很多类似之处,但破坏时对应的轴向应变值明显较常规试验偏低。根据以上研究可知,一些研究认为加卸荷对土体的抗剪强度和模量有明显影响,另一些研究则认为加卸荷对抗剪强度和模量没有明显影响,因此在加卸荷条件对土体力学特性影响的研究方面目前并无统一结论。

通过分析已有文献发现,考虑地下结构相互交叠复杂卸荷条件下土体力学特性的试验研究不多。一些研究针对预剪应力的影响对原始的Duncan-Chang模型进行了修正,但未考虑卸荷及预剪应力对模型中土体切线模量的影响,因此有必要对此开展深入研究。本研究利用GDS动静三轴仪,通过对杭州淤泥质黏土的卸荷三轴剪切试验,研究竖向和水平向同时卸荷时复杂卸荷工况下土体的强度与变形特性,并考虑卸荷及预剪应力对应力-应变曲线公式和初始切线模量的影响,建立了修正的Duncan-Chang模型。

1 试验土样

试验所用淤泥质黏土试样取自杭州市某城市道路隧道与地铁隧道相互交叠的工程现场,地铁隧道先行完工,两隧道近乎垂直交叠,其典型纵断面图见图1。土样为工程地质剖面③1层的淤泥质黏土,土样的主要物理力学性质指标见表1。

表1 土样的主要物理力学性质指标Table 1 Main physical and mechanical property indices of soil specimen

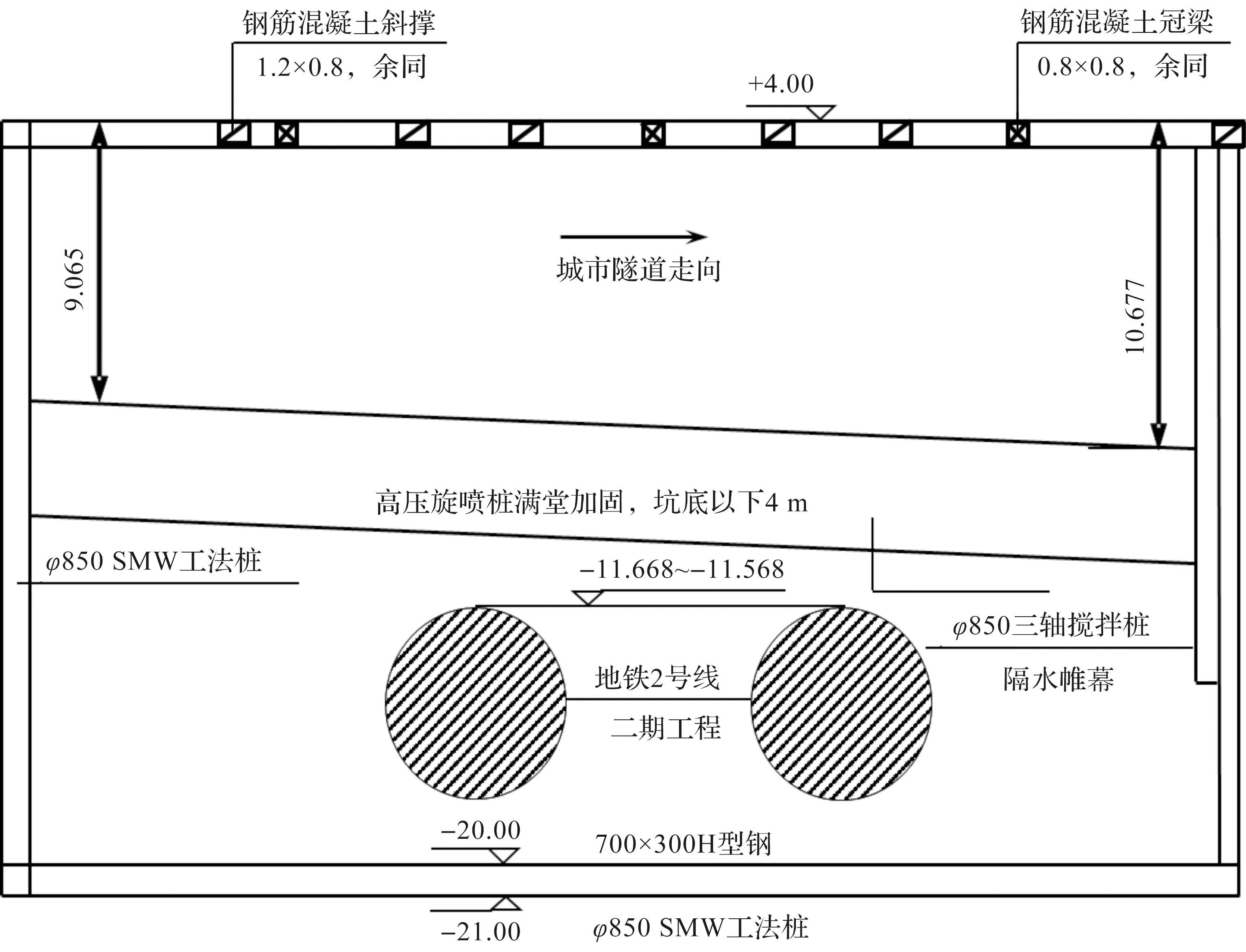
图1 城市道路隧道与地铁隧道相互交叠典型纵断面图(单位:m)Fig.1 Typical longitudinal cross-section of city road tunnel and metro tunnel crossing (unit: m)

2 试验方案

土样采用K0固结,初始围压σ3采用200 kPa,根据地区经验,侧压力系数K0取0.8,即初始轴压σ1采用250 kPa。为合理模拟隧道交叠位置不同区域土体的应力路径变化,在对土样进行剪切前,考虑以下3种应力卸荷情况进行对比分析:1) 卸荷路径A:轴压不变,即Δσ1=0,围压减小,即Δσ3>0,因此,Δσ1/Δσ3=0;2) 卸荷路径B:其卸荷应力比Δσ1/Δσ3=2;3) 卸荷路径C:卸荷应力比Δσ1/Δσ3≈2.67。卸荷路径A、B、C的卸荷再剪切试验步骤见表2～4,其中卸荷1和2分别表示开挖上部城市道路隧道和下部地铁隧道引起的卸荷。试验中,卸荷阶段卸荷速率采用应力控制方式,再剪切阶段加荷速率采用应变控制方式。

表2 卸荷路径A的卸荷再剪切试验步骤Table 2 Unloading and reshearing test procedures of unloading path A

表3 卸荷路径B的卸荷再剪切试验步骤Table 3 Unloading and reshearing test procedures of unloading path B

表4 卸荷路径C的卸荷再剪切试验步骤Table 4 Unloading and reshearing test procedures of unloading path C

3 不同卸荷条件下淤泥质黏土应力-应变特性

不同卸荷路径下淤泥质黏土卸荷后再剪切应力-应变曲线如图2所示。由图2可知,3种卸荷应力路径下,偏应力差(σ1-σ3)与轴向应变εa均呈双曲线关系,峰值抗剪强度随卸荷应力比的增大而增大,说明剪切前预剪应力越大,其峰值强度越低;当卸荷应力比较大时,存在一定的应变软化现象,与弱超固结黏性土的应力-应变特性接近,但总体而言,其应变软化现象并不明显。

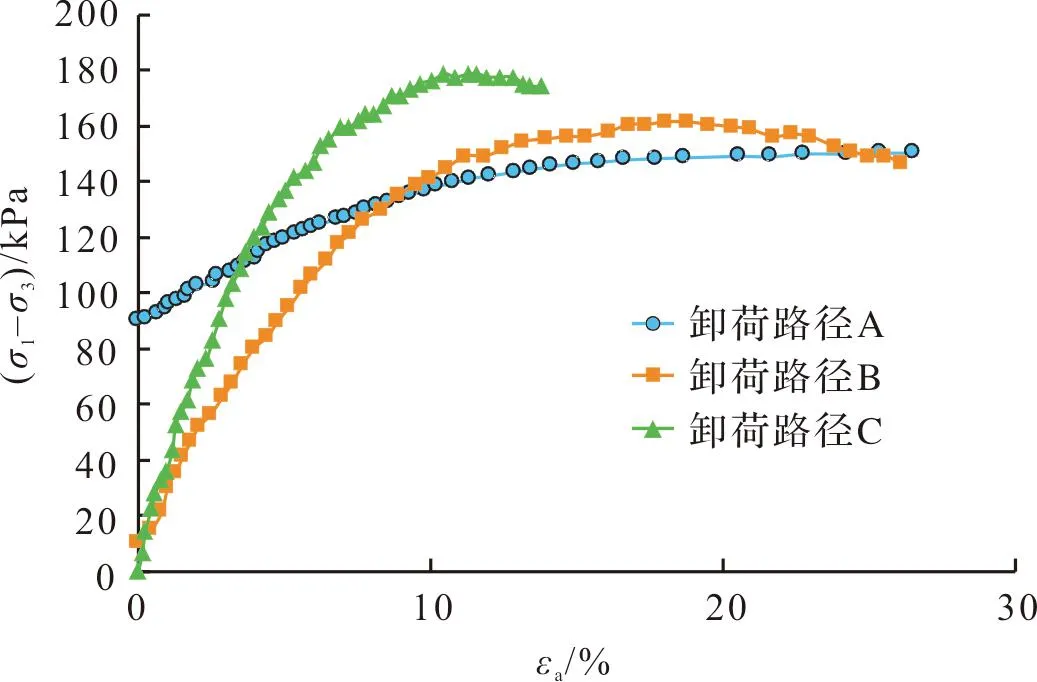
图2 不同卸荷路径下淤泥质黏土卸荷后再剪切应力-应变曲线Fig.2 Post-unloading and reshearing stress-strain curves of very soft clay under different unloading paths

4 不同卸荷条件下淤泥质黏土三轴试验应力路径

根据不同卸荷路径下淤泥质黏土的试验结果,可以绘制土样固结—卸荷—再剪切整个阶段的应力路径,如图3所示,图中p=(σ1+σ3)/2,q=(σ1-σ3)/2。不同土样的应力路径均从K0固结线的同一点出发,在卸荷与再剪切过程经历不同的p-q变化,最终均到达Kf线发生剪切破坏。根据试验结果可以拟合出相关系数较高(R2=0.999)的Kf线,其方程如下:

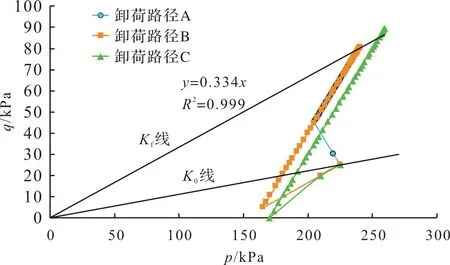
图3 不同卸荷路径下淤泥质黏土的固结—卸荷—再剪切应力路径Fig.3 Consolidation-unloading-reshearing stress paths of very soft clay under different unloading paths

qf=0.334pf。

(1)

由土体的摩尔-库伦破坏准则可知:

(2)

式(2)中:c和φ分别为土的黏聚力和内摩擦角。

式(2)可以改写为

qf=sinφpf+ccosφ。

(3)

对比式(1)和(3)可得,杭州淤泥质黏土的三轴试验总应力抗剪强度参数为

c=0,φ≈19.5°。

(4)

式(4)中:c=0,这说明3种不同卸荷路径对淤泥质黏土的黏聚力并无影响,其黏聚力值和正常固结黏性土的黏聚力性状相似。得出的抗剪强度参数值可用于考虑卸荷和预剪应力影响的修正Duncan-Chang模型。

5 考虑卸荷和预剪应力影响的修正Duncan-Chang模型

Duncan-Chang模型由Duncan和Chang[10]基于Kondner的研究结果[11]提出。原始的Duncan-Chang模型是基于等压固结三轴试验结果拟合建立的,一些研究者在应力-应变双曲线公式中考虑了剪切前预剪应力的影响对其进行了修正[2,4,8,12-15],但未能很好地考虑预剪应力及卸荷应力历史对初始切线模量的影响,因此必须在此基础上对模型进行全面修正,才能建立考虑预剪应力及卸荷后再剪切条件下的Duncan-Chang模型。

根据图2中淤泥质黏土K0固结卸荷后的再剪切应力-应变曲线可知,在淤泥质黏土的偏应力达到峰值之前,偏应力(σ1-σ3)与轴向应变(εa)之间的变化关系呈双曲线,符合Duncan-Chang模型的特征,但需考虑偏应力初始值对模型进行修正,即

(5)

式(5)中σ10和σ30分别为再剪切前的大小主应力初始值。

采用εa为横坐标、εa/[(σ1-σ3)-(σ10-σ30)]为纵坐标建立坐标系,可得不同卸荷路径下淤泥质黏土卸荷后再剪切归一化应力-应变曲线,如图4所示。由图4可知εa/[(σ1-σ3)-(σ10-σ30)]与εa基本上呈线性关系,可表示如下:

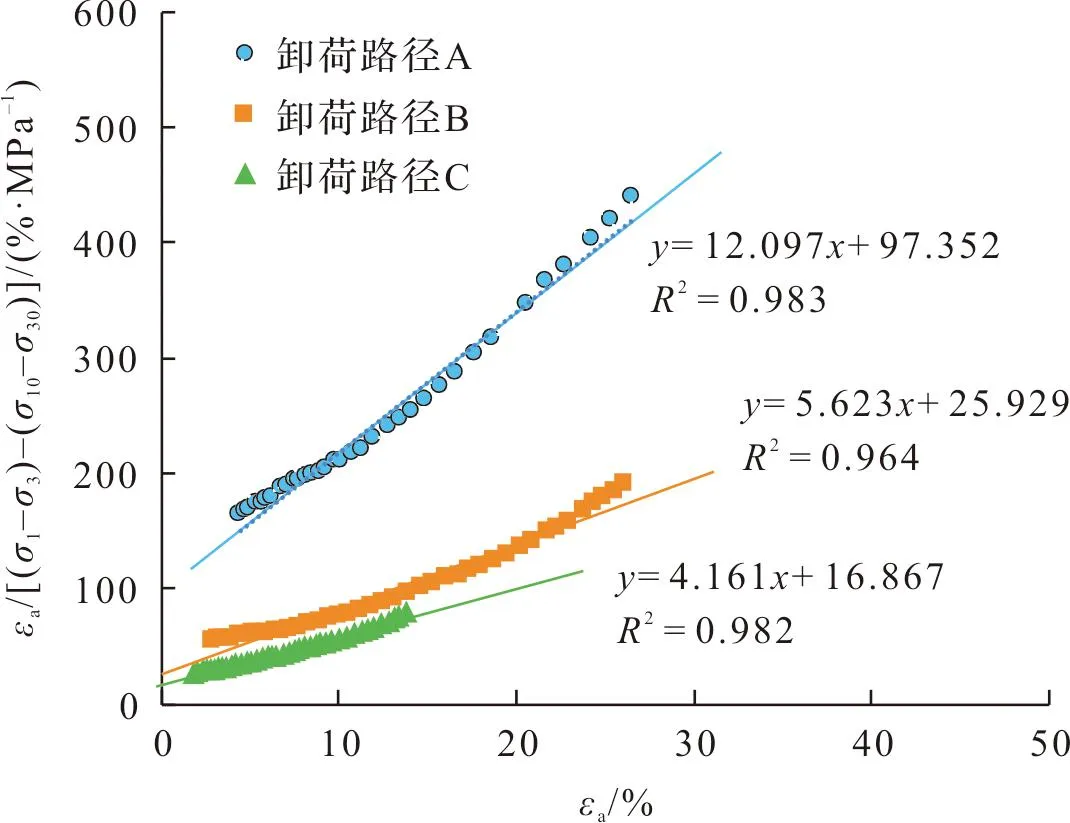
图4 不同卸荷路径下淤泥质黏土卸荷后再剪切归一化应力-应变曲线Fig.4 Normalized post-unloading and reshearing stress-strain curves of very soft clay under different unloading paths

(6)

式(6)中:a为拟合直线的截距;b为拟合直线的斜率。

式(5)还可改写成:

(7)

由式(7)可知,当轴向应变εa→∞时,偏应力趋向于极限值(σ1-σ3)ult,于是

(8)

土样破坏时的偏应力与极限值之比称为破坏比,令其为Rf。若土样破坏时的偏应力为(σ1-σ3)f,则考虑预剪应力的破坏比可以定义如下:

(9)

将式(8)代入式(9)得

(10)

将式(5)求导,可得切线模量为

(11)

令εa=0,则原点的切线模量,即初始切线模量为

(12)

将式(10)和式(12)代入式(5)得

(13)

同理可得切线模量为

(14)

从式(13)可得:

(15)

将式(15)代入式(14)得

Et=(1-RfS)2Ei。

(16)

其中

(17)

式(17)中:S为应力水平。

根据摩尔-库伦破坏准则得

(18)

将式(18)代入式(17)和(16)可得:

(19)

通常,按照原始的Duncan-Chang模型,初始切线模量

(20)

当存在卸荷和预剪应力时,按式(20)或将式(20)中的σ3c替换成σ30,根据试验数据在Excel中对初始切线模量公式进行对数线性拟合,发现相关系数较低,线性拟合效果不好,因而需考虑卸荷和预剪应力的影响对上述初始切线模量公式进行修正。根据不同卸荷路径下淤泥质黏土初始切线模量试验数据进行归一化拟合后的结果(图5),初始切线模量

(21)

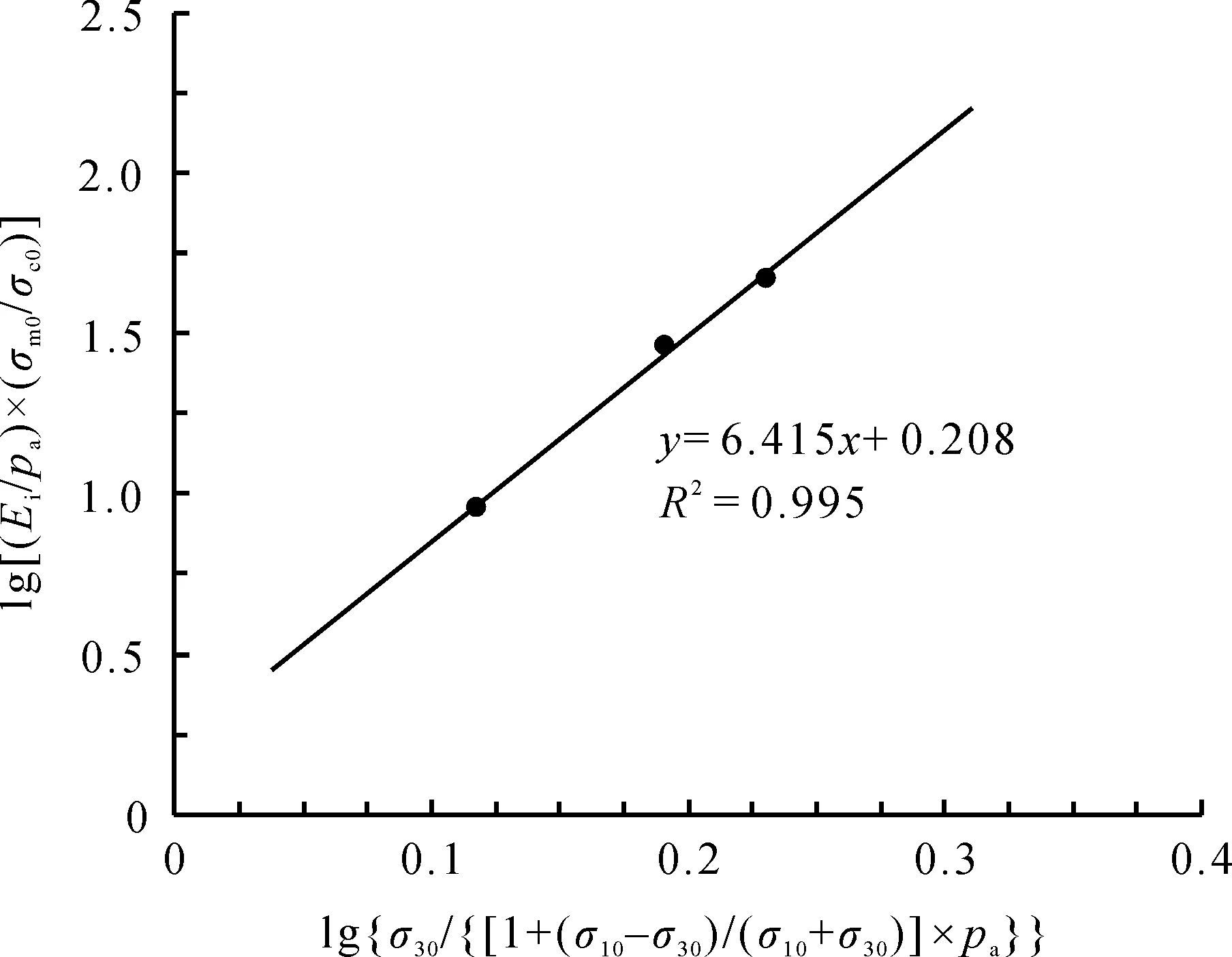
图5 不同卸荷路径下淤泥质黏土初始切线模量试验数据归一化拟合Fig.5 Normalized fitting of initial tangent modulus test data of very soft clay under different unloading paths

式(21)中:pa为大气压力;K、n均为试验常数,根据图(5)的拟合直线方程可得,K=100.208≈1.615,n≈6.415;σmc和σm0分别为固结后和再剪切前的平均围压,σmc=(σ1c+σ2c+σ3c)/3,σm0=(σ10+σ20+σ30)/3。对于常规三轴试验,σmc=(σ1c+2σ3c)/3,σm0=(σ10+2σ30)/3。

对于固结后再剪切前不存在加卸荷的情况,σm0=σmc,σ30=σ3c,σ10=σ1c,式(21)可简化为

(22)

如果再剪切前土体处于K0固结状态,则σ3c=K0σ1c,式(22)可表示为

(23)

如果再剪切前土体处于等压固结状态,则σ1c=σ3c,则式(22)退化为式(20)。

对于等压固结且等压卸荷的情况,σ10=σ30,σmc=σ3c,σm0=σ30,式(21)可简化为

(24)

因此,式(21)为适用于各种加卸荷条件的通用初始切线模量表达式。

将式(21)代入式(19),可得考虑预剪应力及卸荷后再剪切的Duncan-Chang模型的切线模量表达式:

(25)

根据本文的K0固结卸荷后再剪切试验研究结果,结合图4和图5的拟合数据,可得不同卸荷路径下淤泥质黏土的Duncan-Chang模型参数,见表5。

表5 不同卸荷路径下淤泥质黏土的Duncan-Chang模型参数Table 5 Duncan-Chang model parameters of very soft clay under different unloading path

根据文献[16],破坏比Rf可取各试验的平均值,故在淤泥质黏土Duncan-Chang模型中,可取Rf=0.775。

总结上述研究结果,杭州淤泥质黏土Duncan-Chang模型通用切线模量表达式如式(25),其中模型中所需的5个参数分别为:Rf=0.775,K=1.615,n=6.415,c=0,φ=19.5°。

6 结 论

本研究通过对杭州淤泥质黏土的卸荷三轴剪切试验,研究竖向和水平向同时卸荷复杂工况下土体的强度与变形特性,分析土体的应力-应变特性及应力路径,并考虑预剪应力及卸荷后再剪切的应力条件,对原始的Duncan-Chang模型进行了修正,得出如下结论:

1) 3种不同卸荷应力比条件下,其应力-应变变化均呈双曲线关系;随着卸荷应力比的增大,其峰值强度逐渐增大,且峰值剪应力对应的轴向应变逐渐减小;当卸荷应力比较大时,存在一定的应变软化现象,但软化现象并不明显。

2) 不同土样的应力路径均从K0固结线的同一个点出发,在卸荷与再剪切过程经历不同的p-q变化,最终均到达Kf线发生剪切破坏;试验数据拟合的Kf线线性相关性较好,根据拟合的Kf线及Mohr-Coulomb破坏准则,可以不用绘制莫尔圆直接得到土的抗剪强度参数。

3) 考虑土体卸荷和预剪应力的影响,对原始的Duncan-Chang模型的应力-应变曲线公式和初始剪切模量进行修正,得到了修正Duncan-Chang模型及杭州淤泥质黏土的模型参数。