基于半连续两部模型的保险损失预测

鲁亚会,刘爱义

(1.浙江科技学院 经济与管理学院,杭州 310023;2.美国国立卫生研究院,美国 贝塞斯达 20817)

保单持有人和保险公司的风险防范意识不断增强,使得大部分保单并不会发生风险,或者保险公司与被保险人签订免赔偿或无赔偿折扣等条约,也使得在发生较轻的事故时被保险人不提出索赔[1]。这会导致一份保单或一个风险类别的累积损失数据具有下述2个特点:一是出现零过多现象,因为大部分保单在保险期间并未产生索赔,即在零点产生一个较大的概率堆积;二是非零部分可假设服从连续分布。此时,若直接采用传统的Tweedie回归模型[2-3]进行累积损失预测,虽然该方法不要求损失次数与损失金额满足相互独立,但其可能会在预测零概率值时产生较大偏差,即由Tweedie分布得到的零概率值远小于累积损失观察值的零概率值。虽然目前也有研究者对Tweedie回归模型进行了改进[4],但是也只能对均值引入协变量,而不能对零概率值引入协变量。可见,Tweedie回归模型在预测累积损失时具有一定的局限性。上述累积损失数据的2个特点其实质上就是一种半连续型数据,这是由于计量数据中包含过多零值时,除零以外的非零观测值往往是连续的,所以被称为半连续数据。对于半连续数据,Madden[5]指出此类型数据可以看作由混合分布产生,即可假设由零值数据(退化分布)和非零连续数据(连续分布)各占一定比例所构成的混合分布所产生[6],目前两部模型是最常用的拟合分析方法[7-8]。对于半连续数据的两部模型,其模型构建的基本思路是将数据看作由2个不同的随机过程产生。第一个过程考虑零值是否出现,即表示某种行为是否发生,此过程通常被称为数据的二元部分,此部分可假设服从伯努利分布[9];第二个过程考虑非零值的产生,此过程通常被称为数据的连续部分,此部分可假设服从一般的连续分布,如正态分布、伽马分布等[10]。为了进一步分析半连续数据中自变量对因变量的影响,需对二元部分参数和连续部分参数分别引入协变量,从而构造半连续两部回归模型[11-12]。因此,基于半连续两部模型,本研究将提出3种不同的累积损失预测模型。即将累积损失看作2个过程进行分别处理:一是损失是否发生,假设服从伯努利分布;二是在损失发生情况下累积损失金额的分布,分别考虑正态分布、伽马分布和逆高斯分布。对累积损失的2个过程分别引入相关的协变量进行解释,从而对累积损失预测建立相应的伯努利-正态(Bernoulli-Normal)回归模型、伯努利-伽马(Bernoulli-Gamma)回归模型和伯努利-逆高斯(Bernoulli-Inverse Gaussian)回归模型。

1 半连续两部回归累积损失模型

基于累积损失数据所具有的特点,其实质上就是一种半连续型数据。在半连续两部模型的框架下,下面将提出3种不同的半连续两部回归累积损失模型。

1.1 模型构建

在一个保险期间,假设X={X1,X2,…,Xn}为保单的累积损失金额,其中Xi(i=1,2,…,n)表示第i份保单的累积损失金额,n为保单总份数[13]。此时,可将累积损失X看作2个过程分别进行处理:1) 损失是否发生,假设服从伯努利分布;2) 损失发生情况下,假设累积损失金额服从不同的分布。由此可对X构建半连续两部模型:

f(xi)=(1-π)I(xi=0)+[πg(xi|xi>0;μ,σ,κ)]I(xi>0),xi≥0,i=1,2,…,n。

(1)

式(1)中:π=Pr(X>0)为非零概率值,且0≤π≤1;I(·)为示性函数;g(X|X>0)为X>0部分选定的连续分布函数;μ为位置参数;σ>0为尺度参数;κ∈R为形状/偏度参数。

另外,在累积损失预测问题中,研究者往往更关注零概率值。因此,记ν=1-π,并将其代入式(1)中。经过整理,则式(1)转换为

f(xi)=νI(xi=0)+[(1-ν)g(xi|xi>0;μ,σ,κ)]I(xi>0),xi≥0,i=1,2,…,n。

(2)

式(2)中:ν=Pr(X=0)为零概率值。对非零累积损失数据的连续分布函数g(X|X>0),下面将分别采用正态分布(一般需进行对数转换)、伽马分布和逆高斯分布进行拟合分析。

1.2 伯努利-正态回归累积损失模型

在半连续两部模型(2)中,假设X>0部分服从正态分布N(μ,σ2),且考虑到X>0部分具有一定的偏态性,在实际应用中,一般需对X>0进行对数转换。此时,g(X|X>0)分布的密度函数

(3)

将式(3)代入式(2)中,对累积损失X构建伯努利-正态两部模型,即构建由零点的退化分布和非零的正态分布组合的混合分布,其密度函数

(4)

式(4)中:μ为正态分布的均值,是位置参数;σ>0为正态分布的标准方差,是尺度参数。

为了进一步识别风险,在伯努利-正态两部模型式(4)中,分别对ν和μ引入相关的协变量,从而能够分析不同因素对ν和μ所产生的影响。另外,结合逻辑连接函数和对数连接函数,得到预测累积损失的伯努利-正态回归模型:

(5)

式(5)中:z1i=(z1i0,z1i1,…,z1iq1)T为零概率νi的q1+1维协变量向量;β1=(β10,β11,…,β1q1)T为所对应的q1+1维回归系数向量。z2i=(z2i0,z2i1,…,z2iq2)T为均值参数μi的q2+1维协变量向量;β2=(β20,β21,…,β2q2)T为其所对应的q2+1维回归系数向量。设定z1i0=z2i0=1,则β10和β20分别表示2个子回归部分的截距项。另外,在实际应用中,混合比例νi的协变量z1i和均值参数μi的协变量z2i可以相同,也可以不同。

1.3 伯努利-伽马回归累积损失模型

在半连续两部模型式(2)中,假设X>0部分服从伽马分布G(μ,σ2)。此时,g(X|X>0)分布的密度函数[14]

(6)

将式(6)代入式(2)中,对累积损失X构建伯努利-伽马两部模型,即构建由零点的退化分布和非零的伽马分布组合的混合分布,其密度函数

(7)

式(7)中:μ为伽马分布的均值,是位置参数。

类似于伯努利-正态回归累积损失模型,在伯努利-伽马两部模型式(7)中,对ν和μ分别引入相关的协变量,并结合逻辑连接函数和对数连接函数,得到预测累积损失的伯努利-伽马回归模型:

1.4 伯努利-逆高斯回归累积损失模型

在半连续两部模型式(2)中,假设X>0部分服从逆高斯分布N(μ,σ2)。此时,g(X|X>0)分布的密度函数[15]

(8)

将式(8)代入式(2)中,对累积损失X构建伯努利-逆高斯两部模型,即构建由零点的退化分布和非零的逆高斯分布组合的混合分布,其密度函数

(9)

式(9)中:μ为逆高斯分布的均值,是位置参数。

同样,在伯努利-逆高斯两部模型(9)中,对ν和μ分别引入相关的协变量,并结合逻辑连接函数和对数连接函数,即得到预测累积损失的伯努利-逆高斯回归模型:

2 参数估计

目前,针对半连续两部回归模型的参数估计方法较多,而在实际应用中,具体的参数估计方法需根据调查目的及所选用的模型而定。极大似然法是一种最常用的参数估计方法,其基本算法就是高斯-牛顿(Gauss-Newton)迭代法[16-17]。由于伯努利-伽马和伯努利-逆高斯回归累积损失模型的参数估计过程类似于伯努利-正态回归模型,因此,下面只给出伯努利-正态回归模型的高斯-牛顿迭代估计过程。

基于伯努利-正态回归模型式(5),得到模型的似然函数

(10)

式(10)中:yi=I(xi>0)。

(11)

(12)

(13)

将式(11)～(13)代入伯努利-正态似然函数(10)中,得到其对数似然函数

(14)

式(14)中:

接下来采用高斯-牛顿迭代法分别对l1(β1)和l2(β2,σ)进行参数估计。

2.1 用高斯-牛顿迭代法估计对数似然函数l1(β1)

记参数β1的得分函数

从而得到:

(15)

记参数β1的观测信息阵

从而得到:

(16)

2.2 用高斯-牛顿迭代法估计对数似然函数l2(β2,σ)

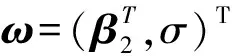
(17)

(18)

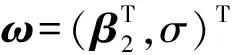
通过计算得到:

(19)

式(19)中:

3 实证研究

下面将本研究所提出的3种半连续两部回归模型和Tweedie回归模型,在一组机动车辆第三者责任险的累积损失数据[18]中进行拟合,以比较4种回归模型的拟合效果。

3.1 数据描述

原始数据集来源于R语言程序包“CASdatasets”,它是一组经典的保险精算数据集,共记录着429 350条损失信息。由于多次损失会发生在同一份保单中,通过累加同一份保单的多次损失,即能够得到累积损失数据集。此外,考虑到预测模型的稳健性,仅将累积损失小于15 000元的保单保留下来,由此共得到412 990份保单作为最终的累积损失数据来源。在这些数据中,共包含397 779份零累积损失保单,因此数据中含有大量的零值,也导致一个很大的零概率堆积。又考虑到数据的偏态性,对累积损失数据中非零值进行对数转换。此时,分别采用Tweedie模型、伯努利-正态两部模型、伯努利-伽马两部模型和伯努利-逆高斯两部模型对累积损失数据进行拟合,并使用AIC(Akaike information criterion,赤池信息量准则)来比较它们的拟合效果。4种模型的AIC值分别为180 652、174 964、177 893和180 483,结果表明:相较于传统的Tweedie模型,3种半连续两部模型具有较好的拟合效果,其中伯努利-正态两部模型又比其他2种两部模型的拟合效果更好。

3.2 模型选择

原始数据中包含着一些连续型和分类型解释变量,其中连续型变量有车龄、驾驶人车龄、人口密度,分类型变量有发动机功率、汽车品牌、汽车油耗类型。各分类解释变量的取值见表1。为了分析不同因素对累积损失产生的影响,对于3种半连续两部模型,将数据中所有解释变量分别引入零概率回归模型和均值回归模型,建立相应的伯努利-正态回归模型、伯努利-伽马回归模型和伯努利-逆高斯回归模型。但是对于Tweedie模型,只能将解释变量引入均值回归模型中,建立Tweedie回归模型。对于本研究所构建的4种回归模型,记l为对数似然函数值,p为模型的参数个数,n为样本容量。采用AIC和BIC(Bayesian information criterion,贝叶斯信息准则)进行模型比较和选择,其中AIC值CAIC=-2l+2p,BIC值CBIC=-2l+plnl,且AIC值和BIC值越小,表明模型具有越好的拟合效果。4种回归模型的拟合优度统计量见表2。

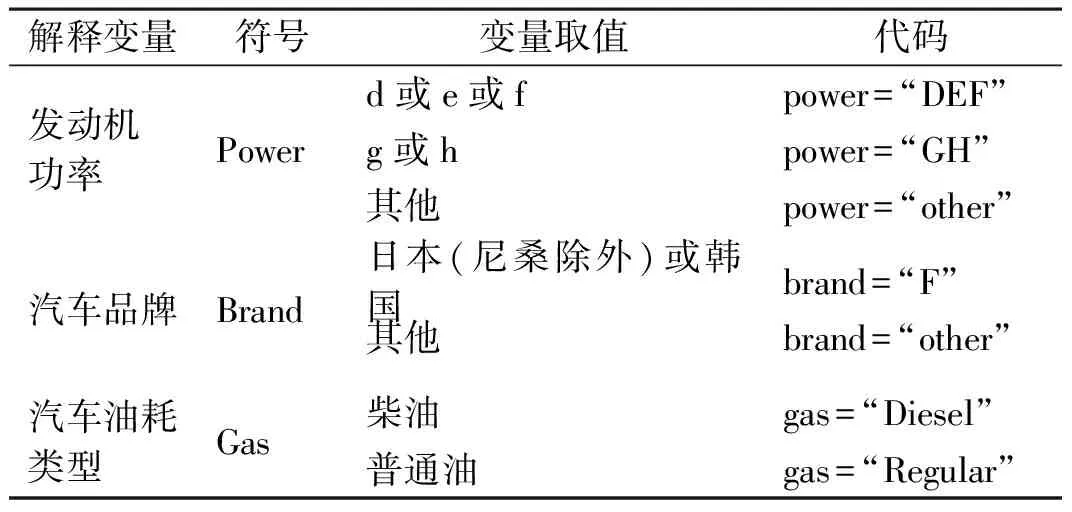
表1 分类解释变量的取值

表2 4种回归模型的拟合优度统计量

由表2可知,3种半连续两部回归模型的AIC值和BIC值都小于Tweedie回归模型,表明半连续两部回归模型对累积损失的拟合效果优于Tweedie回归模型。该结果可能是由于Tweedie回归模型只能对均值建立回归模型,而无法对零概率建立回归模型;半连续两部回归模型能够同时对均值和零概率建立相应的回归模型。另外,在半连续两部回归模型中,伯努利-正态回归模型具有的AIC值和BIC值最小,表明伯努利-正态回归模型的拟合效果优于其他2种回归模型,该结果可能是由于所使用的损失数据并不具有明显的尖峰厚尾特征。

3.3 结果分析

根据4种回归模型的AIC值和BIC值可知,伯努利-正态回归模型对本例的损失数据具有最优的拟合效果。因此,对于本例的累积损失数据,本节将最终建立伯努利-正态回归模型,其中对零概率建立逻辑回归模型,对均值建立对数回归模型,且将原始数据中的解释变量作为2个子回归模型中的协变量集。考虑到连续型变量对零概率和均值产生的影响并不一定是线性的,在伯努利-正态回归模型中,将车龄平方项和驾驶人车龄平方项作为2个子回归模型的协变量,采用高斯-牛顿迭代法进行参数估计。伯努利-正态回归模型的参数估计值见表3。

表3 伯努利-正态回归模型的参数估计值Table 3 Parameter estimates for Bernoulli-Normal regression model

由表3可知,对于零概率回归参数,在显著性水平为5%的情况下,发动机功率、汽车品牌、油耗类型、人口密度、车龄和驾驶人车龄都对零概率具有显著影响,即这些变量都显著影响着损失发生的概率。其中人口密度的估计系数为负值,表明它与零概率存在着负相关,即人口密度值越大,损失发生的可能性也就越大。另外,车龄平方项和驾驶人车龄平方项对零概率也具有显著性影响,但它们的估计符号分别与车龄、驾驶人车龄变量相反,该现象表明车龄和驾驶人车龄对损失发生概率存在非线性影响。对于均值回归参数,在显著性水平为5%的情况下,汽车品牌、油耗类型和驾驶人车龄都对均值具有显著影响,即这些变量都显著影响着累积损失的大小。油耗类型的估计系数为负值,表明它与均值存在着负相关,即汽车油耗类型为普通油时,会减少累积损失的金额。另外,驾驶人车龄平方项对均值也具有显著性影响,且该项的估计符号与驾驶人车龄变量相反,该现象也表明驾驶人车龄对累积损失金额存在非线性影响。

4 结 语

在保险研究中,累积损失预测是厘定纯保费的关键工作,目前最常用的模型就是Tweedie回归模型。但是该模型只能对非零均值建立回归模型,却不能对零概率建立回归模型,从而导致其对累积损失的拟合结果产生偏差。由于累积损失数据往往会出现零过多现象,本研究将该数据视作半连续数据构建模型,并考虑到数据中非零连续部分的分布类型,分别提出伯努利-正态两部模型,伯努利-伽马两部模型和伯努利-逆高斯两部模型。在这3种不同的模型中,对零概率参数和均值参数分别引入相关的协变量,从而建立预测累积损失的伯努利-正态回归模型,伯努利-伽马回归模型和伯努利-逆高斯回归模型。此外,本研究将所提出模型应用于一组机动车辆第三者责任保险的损失数据拟合中,并与传统的Tweedie回归模型进行对比。实证结果表明:相较于Tweedie回归模型,3种半连续两部回归模型具有较好的拟合效果;其中伯努利-正态回归预测模型又优于其他2种模型。

本研究仍存在着一些待进一步探讨的问题。例如,随着信息技术的发展,获取累积损失数据中往往包含大量的候选解释变量,如何在保证模型的准确性和解释性的前提下,更好地选择出更重要的变量子集,这在模型构建中就会产生一个变量选择的问题。因此,半连续两部回归损失预测模型的变量选择将是我们后续研究的重点之一。