路桥斜交接续引发桥台地基的附加应力解析计算

刘鸿源,肖 东,黄 锐

(四川省公路规划勘察设计研究院有限公司,成都 61004)

在路桥设计中,从工程经济性及施工安排上考虑常常要在路基填筑前建造好桥台[1]。当台后路基填筑时会对桥台地基产生附加应力,从而引发桥台的不均匀沉降及桥台前移,影响线路的平顺性,甚至危及上部结构的安全[2-4]。在分析桥台变位时,路基荷载引起的桥台地基附加应力的计算是很重要的一个环节[5]。《铁路桥涵地基和基础设计规范》中提供了适用于单线铁路的路基荷载对桥台地基前后边缘附加竖向应力计算公式及系数表。杨奇等[6]基于弹性力学相关公式及叠加原理详细推导了任一宽度台后路基及锥体对桥台地基产生的附加竖向应力计算公式。蒋关鲁等[7]通过引入路基宽高比系数推导了台后路基荷载下地基附加应力修正计算公式。

以上研究均针对路桥正交接续的情形,而实际工程中,出于对复杂地形、流域、整体线路规划以及施工条件等因素的综合考量,路桥斜交接续的情况时有出现[8],即路基线路中心线与桥台背面处于斜交状态。本文先对斜交路基荷载分布进行合理地简化分解,然后以Boussinesq解为理论基础将分解后的分布荷载所产生的附加应力进行叠加,从而获得了斜交接续时路基荷载引起的地基附加竖向应力计算表达式,并借助Mathematica数学分析软件对不同斜交角下路基荷载引起的桥台地基附加竖向应力的影响规律进行研究,最后与数值分析结果进行了对比。

1 桥台地基附加应力

1.1 基底反力

路基荷载引起的桥台地基附加应力的计算首先需要确定路基基底反力分布,是建立在以下三点假定的基础之上:

(1)台背绝对光滑,不存在摩擦力;

(2)桥台自重引起的应力已转化为原存应力,桥台地基附加应力完全由路基荷载所引起;

(3)路基基底反力采用经路基宽高比修正后的等效路基荷载分布形式[9-10],如图1所示,实线为真实路基轮廓线,虚线为等效路基荷载分布。

图1 路基基底反力

(1)

式中,η1,η2,η3为常数,由地基类型及路基坡度来确定,b为路基顶面宽度,B为路基底面宽度,h为路基高度,γ为路基填土重度,G为路基总荷载,h＇为等效荷载高度,b＇为等效荷载宽度。

1.2 附加应力公式推导

对斜交路基荷载,定义斜交角为路基斜交面与正交面之间的夹角,取逆时针方向为正,路桥正交接续实际上是斜交角α=0的特殊情况。图2为斜交路基荷载的分解示意图,将其划分为三个部分,分别为正交路基荷载和两个三角形区域分布荷载。由叠加原理,斜交路基荷载在地基中任意一点所产生的附加应力即为正交路基荷载与两三角形区域分布荷载在该点产生的应力之和,即:

图2 过渡段斜交路基荷载分解示意

σα=σ0-(σ1+σ2)+(σ3+σ4)

(2)

这里,正交路基荷载引起的附加竖向应力σ0由图1中的①、②及③所产生的附加应力叠加得到。式(3)为σ0的解析表达式,其详细推导过程参见文献[7],式中各参数含义在图1、图3中有明确表示。

图3 三角形区域荷载分布平面坐标

σ0=σz1+σz2+σz3

(3)

(3.1)

(3.2)

(3.3)

其中:

接下来建立σ1、σ2、σ3及σ4(分别代表△ABC、□BCED、△AB＇C＇及□B＇C＇E＇D＇分布荷载产生的附加竖向应力)的数学表达式。图3为三角形区域分布荷载在水平面上的投影,将图1、3统一起来实际上是一空间直角坐标系,O点为坐标原点,x轴垂直于路基中心线,向右为正,y轴平行于路基中心线,远离桥台方向为正,z轴为竖直方向,向下为正。A点(x0,y0,0)为斜交面与路基中心线的交点。另外,为简化积分表达式,将应力计算点定在原点O所在的垂线上(0,0,z0),而计算点的任意性通过改变x0、y0、z0的值来实现。在土力学中,半无限土体表面一定面积F上作用一分布荷载p(ξ,η),对土中某点(x,y,z)产生的竖向应力,由Boussinesq解积分可得:

(4)

在图3中,△ABC(Ⅰ)与△AB＇C＇(Ⅲ)上都为均布荷载p,□BCED(Ⅱ) 与□B＇C＇E＇D＇(Ⅳ)上为线性分布荷载,分别为(b＇/2-x0+a＇-x)p/a＇、 (b＇/2+x0+a＇+x)p/a＇,且4个积分域罗列如下:

积分区间△ABC(Ⅰ)为

积分区间□BCED(Ⅱ)为

积分区间△AB＇C＇(Ⅲ)为

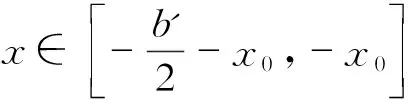
积分区间□B＇C＇E＇D＇(Ⅳ)为

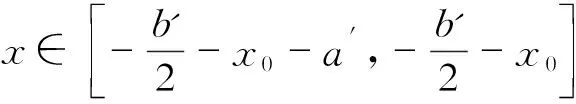
然后将应力计算点坐标O(0,0,z0)、各区域荷载分布函数及积分域分别带入式(4)中,得:

(5)

(6)

(7)

(8)

式(5)～(8)的解析式可采用极坐标法进行积分求得,但积分过程十分繁复且解析表达式过于复杂,实际在计算时可借助数学分析软件Mathematica内嵌的NIntegrate数值积分功能进行计算。

2 计算方法验证与分析

为了直观地反映斜交角对路基荷载下桥台地基附加竖向应力的影响规律,同时检验式(2)的准确性,笔者以铁路标准路基断面作为算例进行计算分析。标准路基断面参数包括:顶宽b= 8.6 m,填高h= 6 m,边坡坡度i= 1∶1.5,路堤填土重度γ= 20 kN/m3。图4为正、斜交接续时路桥过渡段平面简图,ω为桥台宽度。

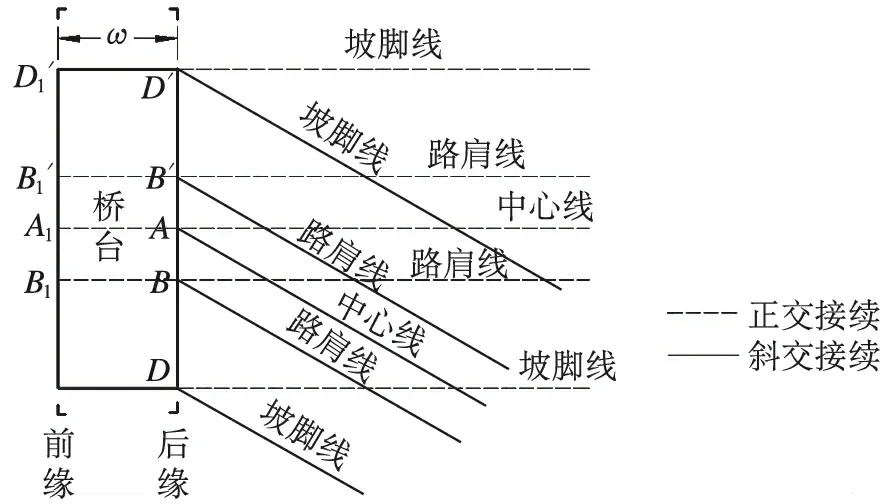
图4 桥台地基附加应力计算点分布

再由式(1)经宽高比修正后,得到修正系数η=0.63 + (0.37b/h) / (1.1+b/h),等效路基荷载参数即可确定:a′=5.63m,b′=15.34m,h′=5.04m。图5为由式(2)计算得到的斜交角α=45°和α=0°(正交接续)桥台前、后缘各控制点附加竖向应力沿深度的变化曲线对比图。

图5 桥台地基各控制点附加竖向应力分布

从图5(a)～(e)可以看出,桥台各控制点前缘与后缘的附加应力不论是空间分布形态还是应力值大小都存在较大差异,且随桥台宽度ω及路基填高的增加,这种差异越明显。这是导致桥台前移一个重要原因[12]。对比斜交角45°与正交接续时桥台地基附加应力分布情况,在图(a)中,由于△ADE和△AD′E′分布荷载在对称点A点处产生的附加应力正好抵消,故在正交与45°工况下点A的附加竖向应力发生重叠,即A点的应力分布不受斜交角的影响,这同时也检验了前述计算方法的正确性。

图6为桥台后缘不同深度处(0.5m、6m、12m及30m)地基附加应力随斜交角的变化规律。从图6看出,斜交角的存在对路基荷载下桥台地基附加竖向应力沿台背后缘的分布产生了影响,具体表现为:当α=0时,桥台后缘的附加应力各深度处均以A点对称分布;当α≠0时,不论斜交角及计算深度的大小,路基中心线以左(D′一侧)的桥台地基附加竖向应力均小于正交接续时所产生的附加应力,而路基中心线以右时(D一侧)的情况正好相反,这相当于台背附加应力分布以A点(A点的附加应力不受斜交角的影响)为中心发生了“偏转”,打破了其沿线路中心对称分布的特性;与正交接续相比,对于斜交面上以A点对称的计算点,同一深度处左侧应力的减小量与右侧的增加量是相等的,且应力的增量随距离线路中心距离的增加而增大,至坡脚线位置达到最大,这一变化规律随着斜交角的增大越趋明显。而不同深度处,斜交角对桥台地基附加竖向应力的影响程度不同。在深度0.5m处,不同斜交角下桥台地基附加应力沿台背分布基本重合,随着深度的增加,斜交角引起的台背附加竖向应力偏转现象变得显著,在深度12m以下,应力偏转现象又趋于平缓。

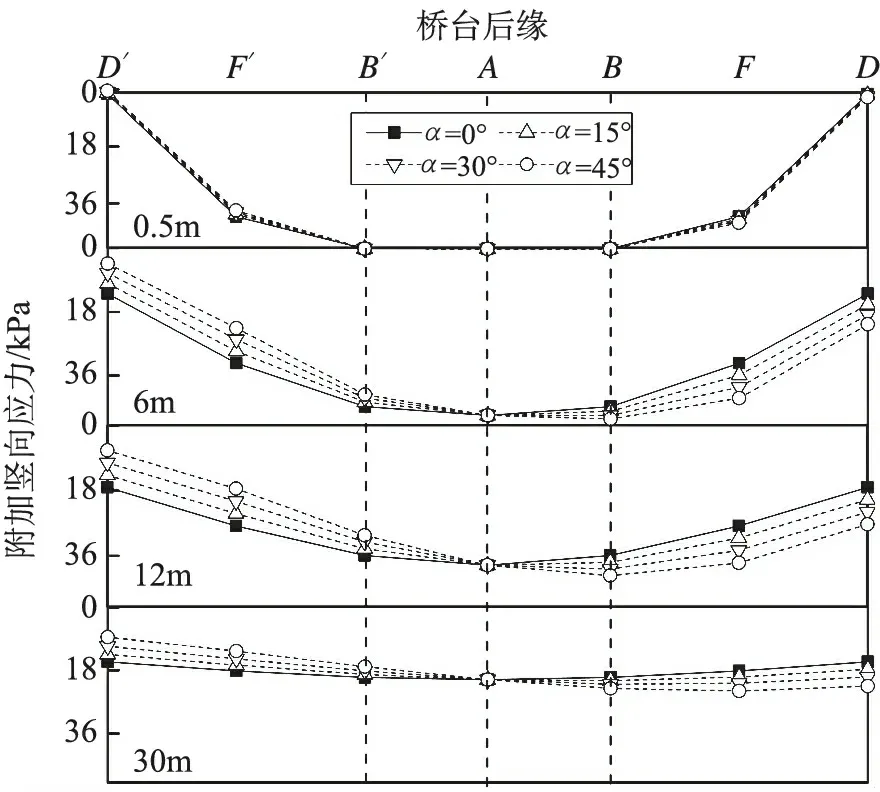
图6 台背不同深度处地基附加应力随斜交角变化曲线

可见,路桥接续时过大的斜交角会导致应力偏转现象加剧,即路桥交界处附近沿线路中心两侧的附加竖向应力差异值越大,对于软基高填方桥台,这不仅会导致桥台朝向附加应力较大一侧产生侧移,也会造成台后路基沿水流方向的差异沉降,故为了减小路基填筑引发的桥台变位和路基差异沉降,建议设计时尽量减小斜交角的大小。

3 结 论

(1)在Boussinesq解的基础上采用极坐标法推导出任意斜交角及任意路基断面形式下考虑路基宽高比影响的附加竖向应力通用计算式,为路基荷载下桥台地基附加应力计算奠定了理论基础。

(2)该法适合计算机编程,并通过自编Mathematica程序运行得出不同斜交角下桥台地基附加竖向应力分布规律,同时与正交接续进行对比分析,验证了计算推导过程及方法的可靠性。

(3)斜交角使得桥台地基附加应力分布沿路基中心线发生偏转,打破了应力沿路基中心对称分布的特性,且随着斜交角的增大,应力偏转现象加剧,这会造成桥台侧移及台后路基差异沉降,对于软基高填方桥台,建议设计时尽量减小斜交角的大小。