基于ANSYS 的新能源汽车转向万向节拓扑优化设计

张金阳，何云峰，史玉锋，向瑞，禹顺安，石占魁

（200093 上海 上海理工大学 机械工程学院）

0 引言

汽车电动助力转向系统因其低廉的成本，在汽车工业领域得到广泛应用[1]。随着新能源汽车的兴起，汽车在运行过程中的安全性、稳定性以及转向的精准性，要求汽车转向系统具有更高的性能。轻量化设计对提高汽车转向系统的性能以及整车的性能有重要的影响。

目前，拓扑优化技术是概念设计阶段最有效的结构轻量化优化技术，也是广泛应用于各领域的优化方法[2]。拓扑优化设计是在特定约束以及负载下通过给定的性能指标在零件目标区域内进行优化。通过数学计算，使得满足性能指标的最小拓扑结构被计算得到。针对汽车电动助力转向系统，一些学者进行了相关的研究。潘乙山等[3]通过坐标变换方法，推导出双十字轴式万向节中间轴的弯矩及中间轴滑动力公式；姜子敬等[4]从设计思路、材料和选型、结构设计和性能仿真分析全方面考量，设计并验证了铝基复合材料转向节的结构和性能，可实现转向节35%的减重；文桂林等[5]系统综述了涉及材料非线性、几何非线性和边界非线性3 种类型的连续体拓扑优化方法，并对现有典型方法进行讨论和评述。

本文以某新能源小型汽车转向系统中的转向万向节零件为研究对象，首先运用SolidWorks 软件，构建三维模型，然后运用ANSYS 软件的拓扑优化模块进行有限元模型搭建以及拓扑优化，分析对比优化前后的静力学特性以及前3 阶模态的影响，以验证优化的综合性能。

1 拓扑优化设计理论模型

在进行拓扑优化时，应当采用综合考虑结构尺寸、形状及拓扑的优化设计方法。在约束方面，应当考虑应力约束、位移约束以及最小构件尺寸约束，结束问题表达式为[6]

式 中：X1=(x1,x2,…,xn)T，X2=(xn+1,xn+2,…,xm)T，X3=(xm+1,xm+2,…,xl)T；X——优化整体变量；X1——结构的拓扑变量；X2——结构的形状变量；X3——结构的尺寸变量；H——结构质量；σmax——结构所有单元中的最大应力；[σ]——结构的许用应力；δ——结构施加位移约束节点的位移；[δ]——结构位移约束的上限值；l——结构的成员尺寸；lmin——结构制造工艺约束中最小成员尺寸值；XiL，XiU——设计变量Xi（i=1,2,3）的上下限；xj——拓扑优化区域中第j（j=1,2,…,n）个单元的相对密度；xmin——为了防止有限元方程在求解过程中刚度矩阵出现奇异而给定的最小相对密度值[7]。

2 有限元模型建立

汽车自动转向系统如图1 所示。汽车动力转向系统是兼用驾驶员和电机为转向能源的转向系。正常情况下，汽车转向所需能量只有一小部分由驾驶员通过转向盘提供，而大部分是通过动力装置为转向系统提供。常用的动力系统装置有液压系统、电气系统和机械系统动力装置。在动力转向装置失效时，一般还应当能由驾驶员独立承担转向任务。

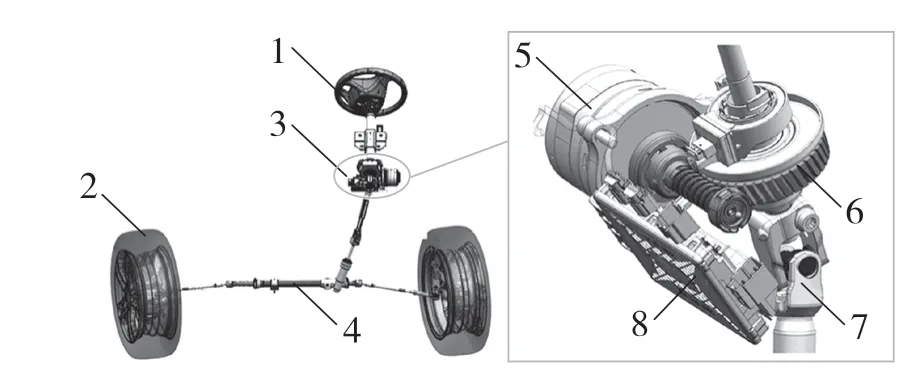
图1 汽车转向系统示意图Fig.1 Schematic diagram of automobile steering system

在转向过程中，转向万向节会受到扭力以及轴向挤压力的作用，因此本文在对转向系统的转向万向节进行拓扑优化时，综合考虑这2 种载荷的作用。利用SolidWorks 软件构建转向万向节的三维模型，如图2 所示，并按要求装配。

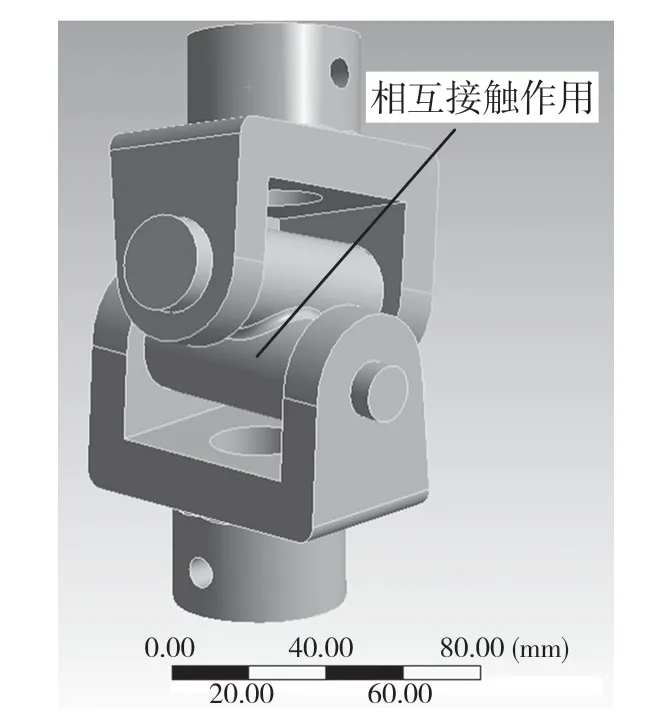
图2 转向万向节模型Fig.2 Steering universal joint model

以某汽车的实际应用参数加载以及万向节材料的选取[8]，具体方式如图3 所示，在万向节输入端加载716 N·m 的扭矩，在万向节输出端加载固定约束。网格划分采用三维应力单元，在优化目标区域可以适当密集，本文选择按尺寸划分，数值为2 mm。选择汽车转向万向节常用的40Cr 定义材料属性，在ANSYS Workbench 中的Static Structural 中进行设置。材料属性如表1 所示，计算单位为长度mm，质量kg，力N，质量密度kg/m3，应力MPa。

表1 转向万向节材料属性Tab.1 Material properties of steering universal joint

图3 载荷添加方式Fig.3 Load adding mode

3 拓扑优化

将接触面以及载荷约束面设置为优化保留区域，将其他部分都设置为优化区域。在ANSYS Workbench 中，通过调用Topology Optimization 插件进行拓扑优化，选择保留材料质量为60%进行计算，迭代结果如图4 所示。

图4 优化结果Fig.4 Optimization results

利用Workbench 的Space Claim 插件对转向万向节模型的轮廓与细节进行修复，使用样条曲线描边，使得零件整体光滑、规整、便于加工。根据拓扑优化结果修复后的零件特征模型如图5 所示。

图5 修复后模型Fig.5 Model after repair

4 原始模型与重构模型对比

为了更好地对比优化前后的性能效果，对优化前后模型的静力学状态以及整体模态进行分析，分析过程中保证材料选择、载荷施加方式以及网格划分的一致性。

4.1 静力学分析对比

优化前转向万向节静力学状态如图6 所示。由图6 可得，优化前最大变形为0.230 49 mm，最大应力为635.11 MPa，最大应变为0.003 248。优化后转向万向节静力学状态如图7 所示，可知最大变形为0.246 95 mm，最大应力为643.22 MPa，最大应变为0.003 25。对比图6 与图7 可以发现，由于材料去除了40%，以及优化后模型的平滑处理，导致在同等载荷与约束的情况下，转向万向节的总体变形、等效最大应力以及等效最大应变略微上升，上升幅度分别是7.1%，0.13%，1.2%，影响都在10%以内，变化幅度在可控范围内。综合考虑静力学分析结果以及轻量化结果，优化后的模型达到了预期效果。

图7 优化后静力学结果Fig.7 Static results after optimization

4.2 前3 阶模态分析对比

对优化前后的汽车转向万向节进行模态求解，得到前3 阶振型云图分别如图8、图9 所示。对比图8、图9 可知，优化前后的转向万向节振型相似，没有太大的改变与破坏。优化前1 阶固有频率891.93 Hz，2 阶固有频率1 359.9 Hz，3 阶固有频率2 442.8 Hz；优化后1 阶固有频率830.92 Hz，2阶固有频率1 266.8 Hz，3 阶固有频率2 032.6 Hz。优化后由于质量减少了40%，前3 阶固有频率有不同程度的下降，但是下降幅度在可控范围内。综合考虑模态分析结果以及轻量化结果，优化后的模型达到了预期的理想效果。

5 结语

本文以某新能源小型汽车转向万向节为研究对象，对其进行拓扑优化设计。在满足其使用性能的前提下，转向万向节零件质量减少了40%。对其静力学特性以及前3 阶模态进行了对比分析，优化前后的转向万向节方案综合影响在10%以内，达到了轻量化设计的目的，实验结果对工程实践具有一定的指导意义。