基于ANSYS Workbench 的一种提取结构骨架的新方法

董宣廷，王瀚，李天箭

（200093 上海市 上海理工大学 机械工程学院）

0 引言

近年来，有限元分析方法在工程设计尤其是拓扑结构设计领域的地位越来越重要，但是拓扑优化得到的结构几何形状往往比较复杂，常用的制造工艺难以加工或成本较高，因此需要在实际加工之前对其进一步分析，得到物理属性后对结构进行进一步优化或重构[1]。由于结构的骨架具有和原本结构相同的拓扑信息和形状特征，能够有效地描述原本的结构，因此与骨架相关的方法常被使用。

骨架的提取在计算机图形学、计算几何学、点集拓扑学和图论等跨学科专业中都有非常重要的作用[2]。H.Blum 最早提出中轴算法，即对区域内的每一个点，在边界中搜索到的最近的点多于1 个时，则该点为图像的骨架单元。但该方法比较费时，且对噪声比较敏感，不能保证骨架线的连通[3]。刘俊涛等[4]提出了一种提取物体线形骨架的重要方法。该方法首先计算物体距离变换的梯度，从而得到一个矢量场，可以根据梯度获得物体内部的关键点，其中每一个关键点代表了物体的一个凸部分，之后使用搜索梯度最短路径的方法连接关键点即可得到物体的线形骨架。闫晓磊等[5]采用拓扑细化方法，提取了拓扑结构的骨架构型，并且以此为基础，判定结构中不满足最小尺寸约束的部位，基于改进的BESO 算法，成功实现了对拓扑优化结构的最小尺寸精确控制；周奇才等[6]以二值图像细化算法为基础，提出了基于有限单元8-邻域网格模型的骨架提取算法。在拓扑优化完成后，应用网格模型骨架提取算法，提取拓扑优化模型的网格骨架，找到反映拓扑结构特征的传力关键点，再基于传力关键点连接杆件形成杆系结构，并且根据满应力准则对其进行优化。所得到的杆系结构具有较好的拓扑构型和杆件截面尺寸，所提出的方法也为杆系结构的拓扑优化设计提供了一种新的思路；Zhang 等[7]提出了一种新颖的结合欧氏距离和有序细化算法来提取骨架的方法。文章首先给出了“删除模板”，该模板可以确定一个给定像素点的8 个相邻像素点是否能够删除，并对满足要求的点进行删除，之后再得到物体的骨架。该算法提出的骨架能够正确地保留物体的拓扑结构，并且提取的骨架定位准确，对边界噪声不敏感；Hu 等[8]提出了一种基于点云模型的截面中心点集合的曲线骨架表达，并提出了相应的提取方法。首先提供三维点云模型的距离场的替代方法，然后将其与曲率结合起来，捕捉混合特征点，之后通过引入相关的面和点，将这些混合特征点沿着骨架引导的法线方向移动，以接近局部中心点，通过基于张量的谱系聚类来简化它们，最后将它们连接起来，形成一个主要的连接曲线骨架，再通过去毛刺、修剪等步骤来完善骨架；Li 等[9]提出了一种基于三维图形中轴线的方法，以方便和快速地提取高质量的曲线骨架。主要的中心度测量方法为通过由内向外的演化方案来模拟火灾的传播，与现有的使用由边界到内部的外向演化方案的方法不同，并且提出了抑制影响的措施，能够获得良好、紧凑并且居中的曲线骨架；Cai 等[10]通过分析Snakes 模型中梯度矢量场的分布特征，提出了一种基于拓扑结构和通量的新的骨架提取方法，即计算完临界点的特征值和梯度矢量场的通量后即可准确获得骨架的分布特征，从而有效地提取骨架。该方法不需要对目标图像进行预处理或二值化，能够有效地提取复杂灰度图像的骨架，与传统方法相比，该方法提取精度较高，处理速度较快。

上述的研究主要提出了一些优化或改进的提取结构骨架的方法，然而很少有研究对提取出的骨架进行进一步分析。本文在上述方法的基础上，结合ANSYS Workbench 软件的相关特性，将整个实体结构细分为若干区块进行分析，选择距离每个区块形状中心最近的网格节点作为关键节点，连接形成骨架。提取的结构骨架不仅包括模型的几何拓扑结构、空间形貌特征，还包括结构的变形量以及静刚度矩阵等物理性能特征。以一个三维L 型支架为例，进行有限元分析和拓扑优化，对拓扑优化后的模型进行骨架提取，来证明该骨架提取方法的正确性，并对骨架进行分析，得到相关的物理属性，为后续数据的再利用和结构的参数化重构提供基础。

1 骨架生成

1.1 拓扑优化后模型的数据预处理

首先通过ANSYS Workbench 软件中的Design Modular 模块画出优化实例模型，模型的各项尺寸如图1（a）所示。模型底部使用4 点固定约束，在A表面上施加一个与x 轴垂直同时与-y 方向和-z 方向呈45°、大小为1 kN 的均布载荷F1；在B 表面上施加一个-z 方向同时垂直于x 轴和y 轴，大小为1 kN 的均布载荷F2。分析时使用六面体单元，将网格单元定为1 mm，将设计域离散为28 000 个六面体单元。使用SIMP 方法作为拓扑优化方法，并对优化后的模型在同一位置添加固定约束和载荷，进行静力学分析，得到结构的变形云图如图1（b）所示。

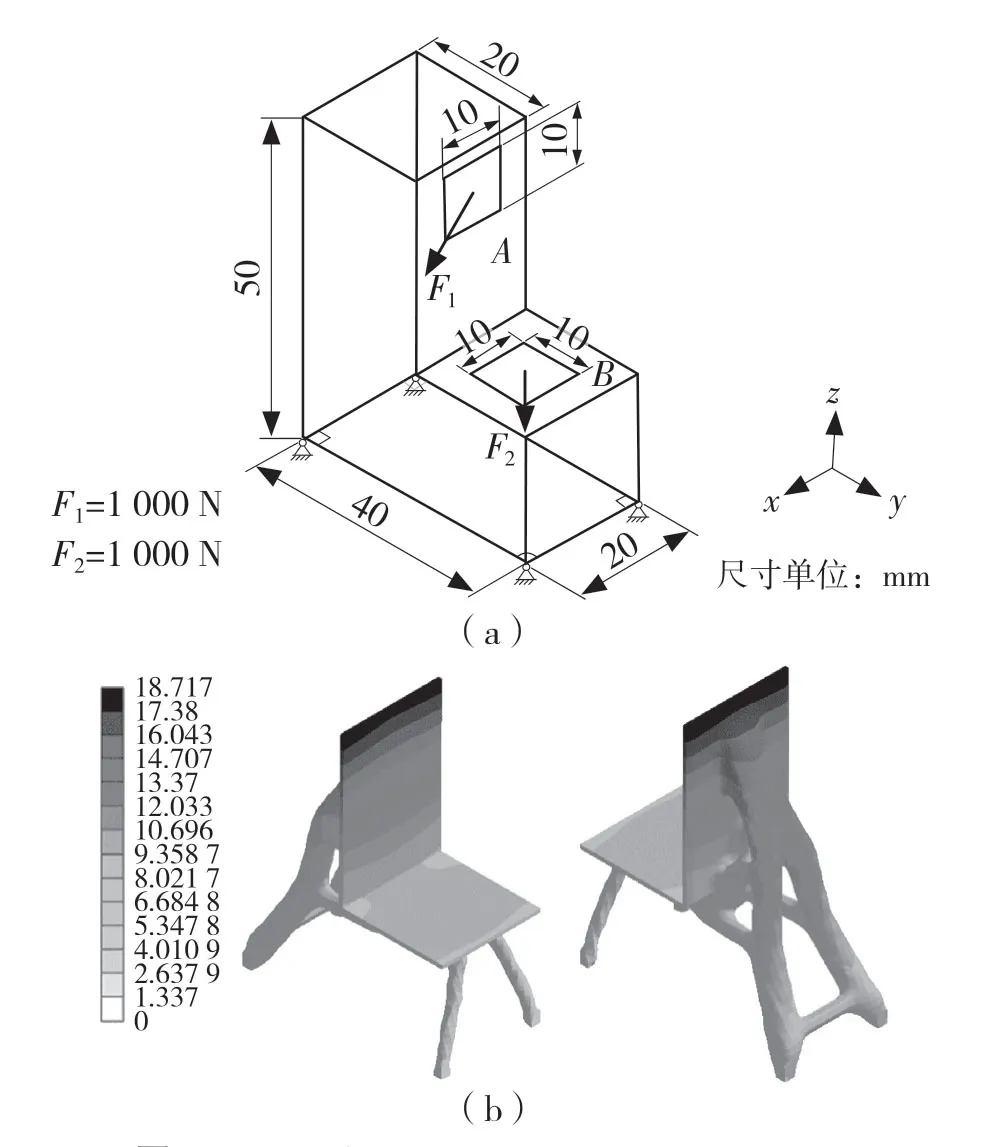
图1 三维L 型支架模型拓扑优化前后模型图及优化后变形云图Fig.1 Comparison of original and optimized 3D L-shaped brackets

之后输出各个节点编号及其对应的x、y、z 坐标值和总变形值大小并且进行记录。分别输出4 个变形大小为0 的固定约束节点对应的节点编号和坐标值，作为骨架的起始节点。将模型的最大变形值记为dmax，最小变形值记为dmin。将整个模型划分为15 个区块，记为Bm（m=1，2，…，15）。将每一个区块所对应的变形量取值范围记为δ，即

在上述15 个区块的基础上，再通过平行于各坐标平面的切片对各个区块进行细分，形成新的区块BNn（n=1，2，…）。对于新形成的区块，需要保证其在后续提取区块内关键节点的过程中只存在唯一节点。

1.2 骨架关键节点的提取过程

由于上述的定义，新获得的区块一定是长方体，分别记录长方体6 个平面对应方向上的坐标，用以计算该区块的中间点坐标。分别将各坐标记为BNnxmax、BNnxmin、BNnymax、BNnymin、BNnzmax、BNnzmin。将各个单连通区域的中间点记为Mn，有

在获取骨架关键节点时，需要优先取区块BNn的中间点并获得其对应坐标，但由于拓扑优化后的模型形状不规则，因此在对其进行有限元分析时网格的划分会不均匀，有可能出现区块的中间点上并不存在网格节点的情况，因此需要取离中间点最近的网格节点作为关键节点。将关键节点记为Kn，BNn内的所有节点记为Tnk（k=1，2，…），Tnk与Mn之间的距离记为distk，Kn与Mn之间的距离记为distmin，即distk取到distmin时对应的Tnk的坐标值即为Kn的坐标值，有

选择模型的其中一个区块来说明关键节点的提取过程，结构示意图如图2 所示。

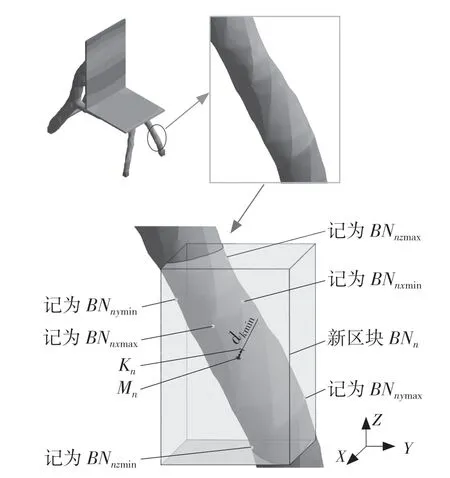
图2 关键节点提取示意图Fig.2 Schematic representation of the calculation process of the key node

1.3 骨架关键节点的连接及骨架的最终生成

记录各点的Kn坐标值后，需要按照顺序连接各个关键节点，连接的方法为：从各个骨架的起始点pt出发，按位移逐渐增大的方向，寻找相邻BNn中的Kn，直到取到位移最大值点所在区块中的关键节点，并按顺序进行连接。如果过程中出现同时有多个区块与上一个区块相邻，则说明该部分存在分支，需要从上一个区块对应的关键节点开始，分别连接各个相邻区块中的关键节点，并分别从各个关键节点（1～5）开始继续搜索，如图3 所示。在所有的关键节点都被选择过后，即所有的pt都被使用过后，所得到的线形模型即为结构的骨架。

图3 分支示意图Fig.3 Schematic diagram of the branches

在骨架连接完成后，会出现某些关键节点被多次使用，并且连接各关键节点的连接线也被反复使用的情况，此时需要对这些多余的部分进行去除，得到完整且没有重复节点和连接线的骨架。

2 结果与讨论

根据上一节中的方法和步骤，最终得到的骨架与模型的叠加，如图4 所示。从图4 可以看出，该方法可以提取出完整的结构骨架，并且可以判断分支的存在。

图4 三维L 型支架骨架图Fig.4 Skeleton diagram of 3D L-shaped bracket

由上文可知，在对模型进行前处理时，所施加的力和所定义的固定约束都是对称的，但结果中依然出现了骨架模型不对称的情况，这是由于在对模型进行区块划分时，可能会出现区块形状不规则的情况。此外，在记录关键点时，所使用的是网格节点，而在划分拓扑优化后模型的网格时，整体网格会呈现不规则分布，因此最后取到的节点无法关于某个平面完全对称，这也使得在最后连接各点形成骨架时会出现骨架节点并不对称的情况，如图5 所示。

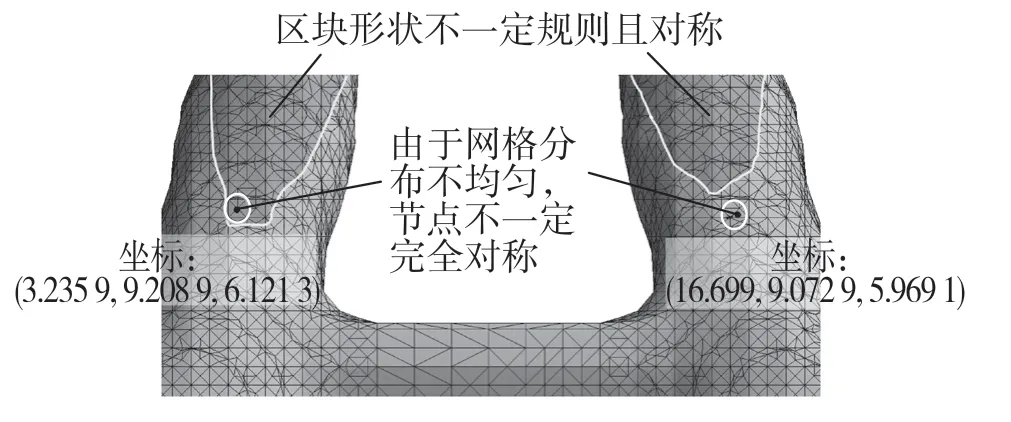
图5 误差分析Fig.5 Analysis of errors

在完成骨架提取后，需要对骨架关键节点上的物理属性进行提取。骨架关键节点的编号、坐标和变形可以由仿真软件直接输出，而各个节点静刚度矩阵的提取需要使用相关的APDL 代码，根据该代码提取出的部分刚度矩阵如表1 所示。具体代码和相关注释为

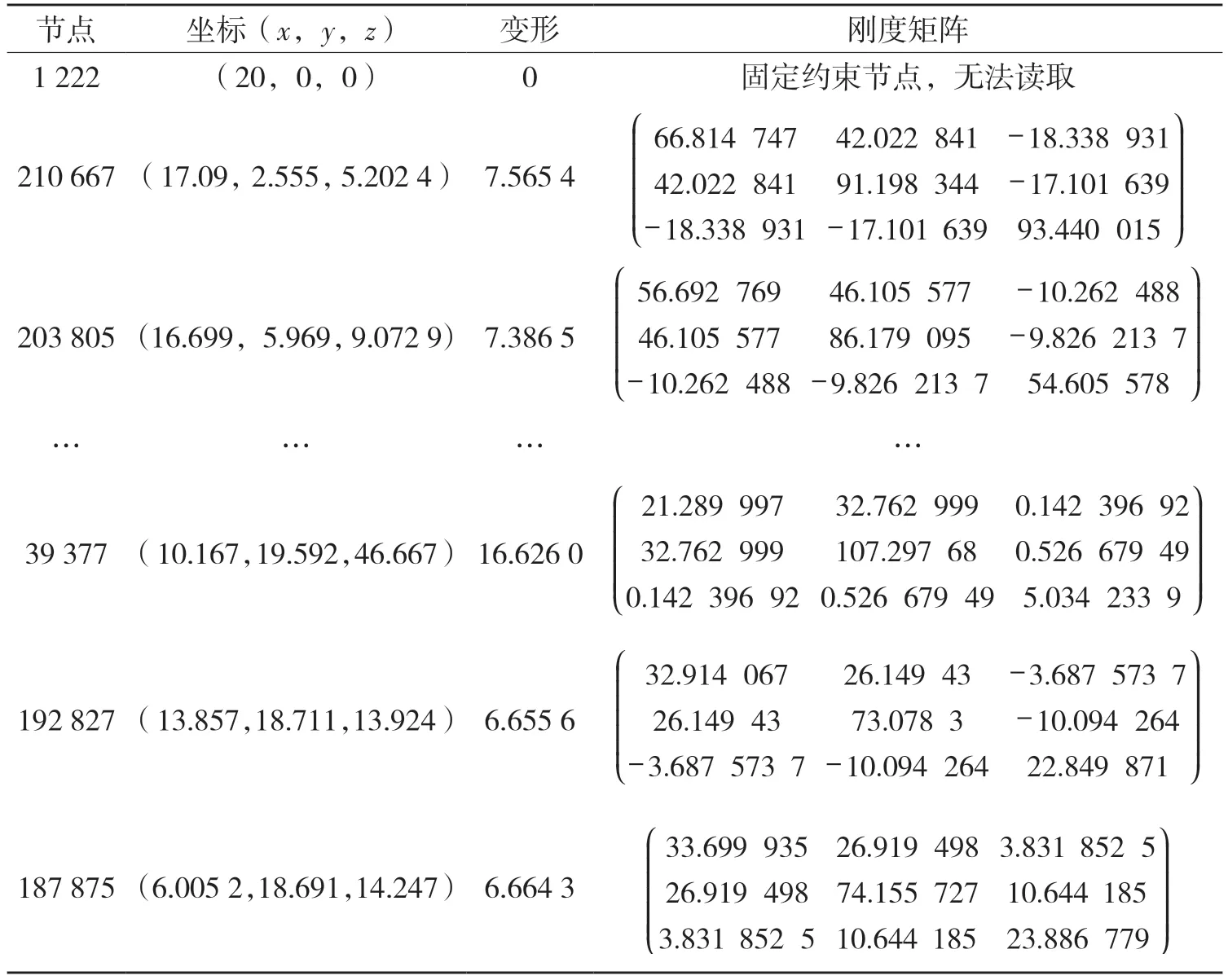
表1 物理属性Tab.1 Physical properties

3 结论

本文提出了一种骨架提取的新方法，并且通过一个三维的算例，对骨架提取的过程进行了说明，得到了如下结论：

（1）该方法可以提出结构中的各关键节点，对各关键节点按顺序进行连接后可以得到结构内部反映其几何形貌特征的骨架；

（2）在完成骨架的提取后，可以通过APDL代码实现骨架各关键节点上物理属性的提取，包括各节点的坐标位置、变形量大小以及静刚度矩阵；

总体而言，用该方法提取的骨架不仅可以获得骨架的几何特征，还可以获得骨架的物理特征。这可以实现基于数据的结构特征描述和存储，为数据的再利用和结构的参数化重构提供了基础。