连接器密封橡胶件加速退化试验研究

陈东旭，徐 乐，张 丽，郭婧宜，翟国富

(1.哈尔滨工业大学电器与电子可靠性研究所，黑龙江哈尔滨，150001；2.中航光电科技股份有限公司，河南洛阳，471000)

1 引言

连接器密封件对于产品的寿命预计与产品的使用安全、高效可靠、成本估量都息息相关。近些年来,伴随着科技信息化的不断更迭,工作稳定、使用寿命长的产品越来越多,产品的更新换代也愈发快速。传统的寿命试验在自然环境下进行,虽然试验数据准确且预测结果具有很强的说服力,但试验的整体用时久,成本较高,不适合在产品换代频率如此之快的当今社会使用,因此,加速寿命试验应运而生。

20世纪60年代,加速寿命试验的概念第一次被提出:在标准的实际操作和理论研究的基础上,使用有关的数学计量模型,在对正常应力水平范围外的加速应力水平下所获得的置信度较高的试验数据进行变换,从而得到产品试样在正常应力水平下特征的估值的一种试验方法,被称为加速寿命试验[1]。

国内外对于橡胶材料及制品的老化进行了大量的研究,可以总结为老化微观机理研究、宏观力学性能分析、加速老化寿命预测和防老化防护方法等4个方面的内容[2]。传统的方法主要有电气工程领域采用的线性关系法、动力学直线化法[3]、时温叠加法、 数学模型法。武汉软件工程职业学院李金玉对氯丁橡胶在空气、海水中的老化实验结果,用非线性回归法处理数据,分别计算了该橡胶在海水和空气中的老化动力学参数[4]。长江大学段家松综述橡胶材料原理,并介绍了用数学模型预测橡胶寿命的一些方法,探索它们的特点及优缺点,提出相关处理方法[5]。吉林大学汽车仿真与控制国家重点实验室刘巧斌等摒弃传统高分子材料老化建模方法的弊端,根据插值法和时温叠加原理,高温加速老化数据外推获得了常温下橡胶老化的平移因子,并建立了常温下橡胶的贮存寿命评估方程,对常温下的贮存寿命进行预测[6]。同济大学机械与能源工程学院张永峰和陆志强等人于2020年提出一种优化的神经网络的寿命预测模型[7]。北京科技大学腐蚀与防护中心吴德权等应用BP神经网络模型,建立了三元乙丙橡胶在中国的自然老化分布预测图[8]。

本文对φ2.65mm O形圈进行了不同温度下和不同压缩量的高温加速老化试验,确定了每个应力环境下O形圈的失效老化因子,建立寿命预测模型,为后续密封用橡胶件加速老化数据处理与寿命预测提供了参考,同时对比出橡胶件在使用过程中不同压缩量对使用寿命的影响。

2 橡胶加速老化试验和退化表征量的计算方法

橡胶的热空气加速老化是最常用的人工加速老化方法,橡胶热空气老化试验的具体实施过程是参照《硫化橡胶或热塑性橡胶热空气加速老化和耐热试验》(GB/T3512-2014)和《恒定应力寿命试验和加速寿命试验方法总则》(GB 2689.1-81)进行的。加速寿命试验中的应力水平应该不少于四个,且各应力水平间应有较大的间隔。其中应有应力水平接近试样在实际应用状态下的应力水平,且最高的应力水平不应超过会导致试样失效的应力水平[9]。故确定试验应力水平为358K(85℃)、378K(105℃)、398K(125℃)和423K(150℃)。本文中的橡胶件实际使用应力水平为25℃。

橡胶退化表征量的宏观性能评价指标有拉伸模量、拉伸截面收缩率、拉伸强度、扯断拉长率、硬度和压缩永久变形率等。对于本文所研究的密封用橡胶圈,其正常工作时处于压缩状态,故采用压缩永久变形率来衡量其老化程度。压缩永久变形率的测量根据《硫化橡胶或热塑性橡胶压缩永久变形的测定》(GB/T7759-2015)的规定进行。压缩永久变形率c的表达式如下:

(2-1)

式中,H0为试样原高,mm;Hn为试样恢复后的高度,mm;Hs,限位器的高度,mm。计算结果精确到0.01%。

3 橡胶老化寿命建模

时温叠加原理是根据化学反应的时间和温度可以相互等效的规律建立起来的,即采用高温来换取反应时间,加快化学反应的速率,换取在短时间内获得材料的性能衰退规律[10]。

实测橡胶件高温加速老化的数据,通过曲线拟合得到不同温度下的压缩永久变形率随老化时间的变化曲线,得到压缩永久变形速率k。

根据阿累尼乌斯方程,橡胶老化速率k满足:

(3-1)

式中:K(T)-反应速率的常数;A-指数因数;E-活化能;R-摩尔气体常数;T-热力学温度。

用Fa表示橡胶件的退化表征量,则在多个水平应力Ti下,橡胶件在在不同的反应时间ti时,以不同的反应速率Ki,达到相同的退化至Fa时:

(3-2)

对上式两边取ln可得:

(3-3)

由此可以得出lnt与温度倒数1/T之间的关系,求得表观活化能E,此时得到不同温度下的橡胶圈压缩永久变形速率的表达式,外推出橡胶件常温下的压缩永久变形速率,选用线性函数c=kT+c0,确定橡胶件压缩永久变形率的失效阈值,从而预测出常温下连接器密封用橡胶件的使用寿命。

3.1 试验方案

在本部分内容中,将对密封用橡胶件的加速寿命试验做出总体的试验方案,内容包括试验类别、试验条件、试样数量、测试参数、试验结果和目的几个部分,并对其中不同的试验类别下橡胶件的压缩量进行计算,该计算应当符合中国船舶工业总公司于1995年发布的标准CB 1236-95中的相关规定。表1是具体的试验方案。

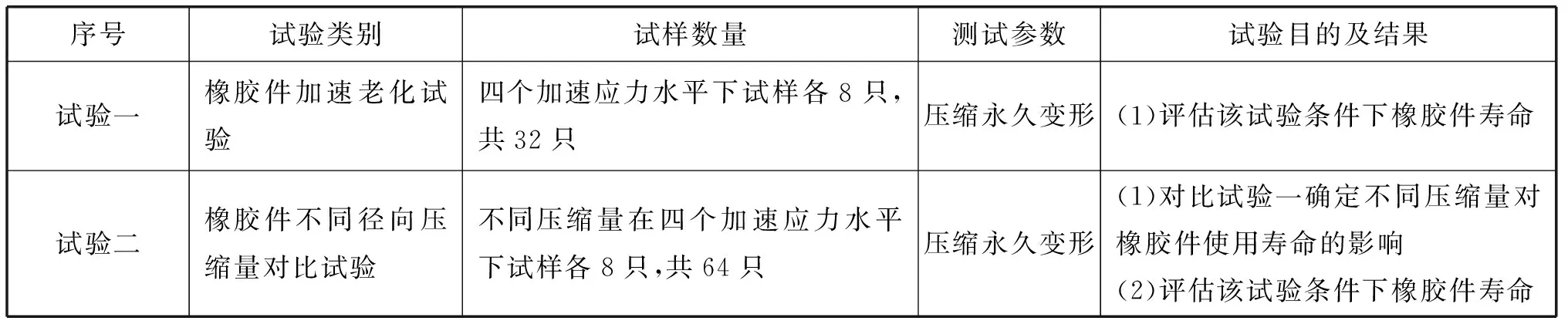
表1 试验方案

实际压缩量计算:计算结果为O形圈压缩量为0.6mm,压缩后高度为2.05mm。

最大压缩量计算:根据CB1236-95中相关规定,最大压缩率Kmax≤26.3%,计算O形圈径向最大压缩量为0.7mm,所以压缩后高度为1.95mm。

最小压缩量计算:根据CB1236-95中相关规定,最小压缩率Kmin≥14.2%,计算O形圈径向最小压缩量为0.38mm,所以压缩后高度为2.27mm。

3.2 夹具设计

在加速寿命试验进行前,根据橡胶件实际使用情况,设计橡胶件夹具,夹具材料采用316不锈钢,防止在试验过程中夹具生锈给试验带来不确定因素,夹具装配图及实物图如图1和2所示。

图1 夹具装配图

图2 夹具实物

3.3 试验数据分析

每个应力水平下的橡胶件试样共八个,处理数据时,首先对每个应力水平下的返回数据进行筛选:算出该组数据的算数平均值后与八个数据依次进行对比,确保每个应力水平下的返回数据与该组数据的平均值的差值不超过10%。之后将该组数据的算数平均值,再计算出压缩永久变形量。

试验时间为320天,橡胶件在实际压缩量、最大压缩量和最小压缩量时,不同温度下的压缩永久变形率随老化时间变化的曲线如图3、4、5所示。

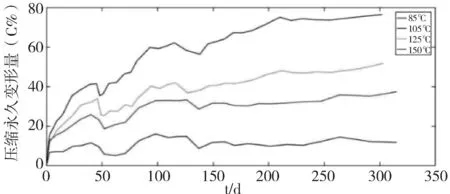
图3 实际压缩量时压缩永久变形率随老化时间变化的曲线

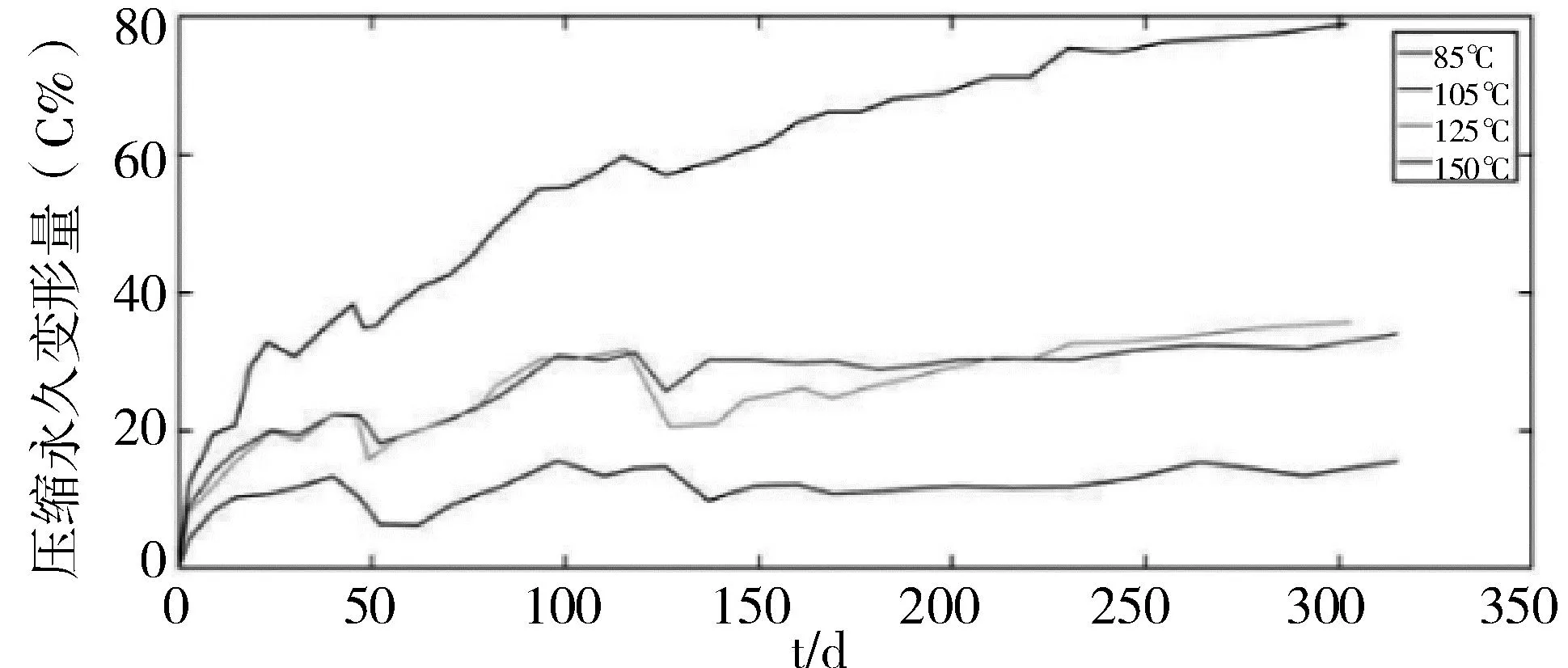
图4 最大压缩量时压缩永久变形率随老化时间变化的曲线

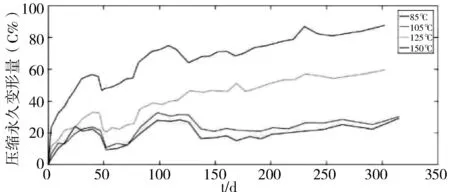
图5 最小压缩量时压缩永久变形率随老化时间变化的曲线

采用动力学直线化法对图3、4、5中不同温度下的加速老化试验数据进行线性拟合,拟合结果如图6、7、8所示。

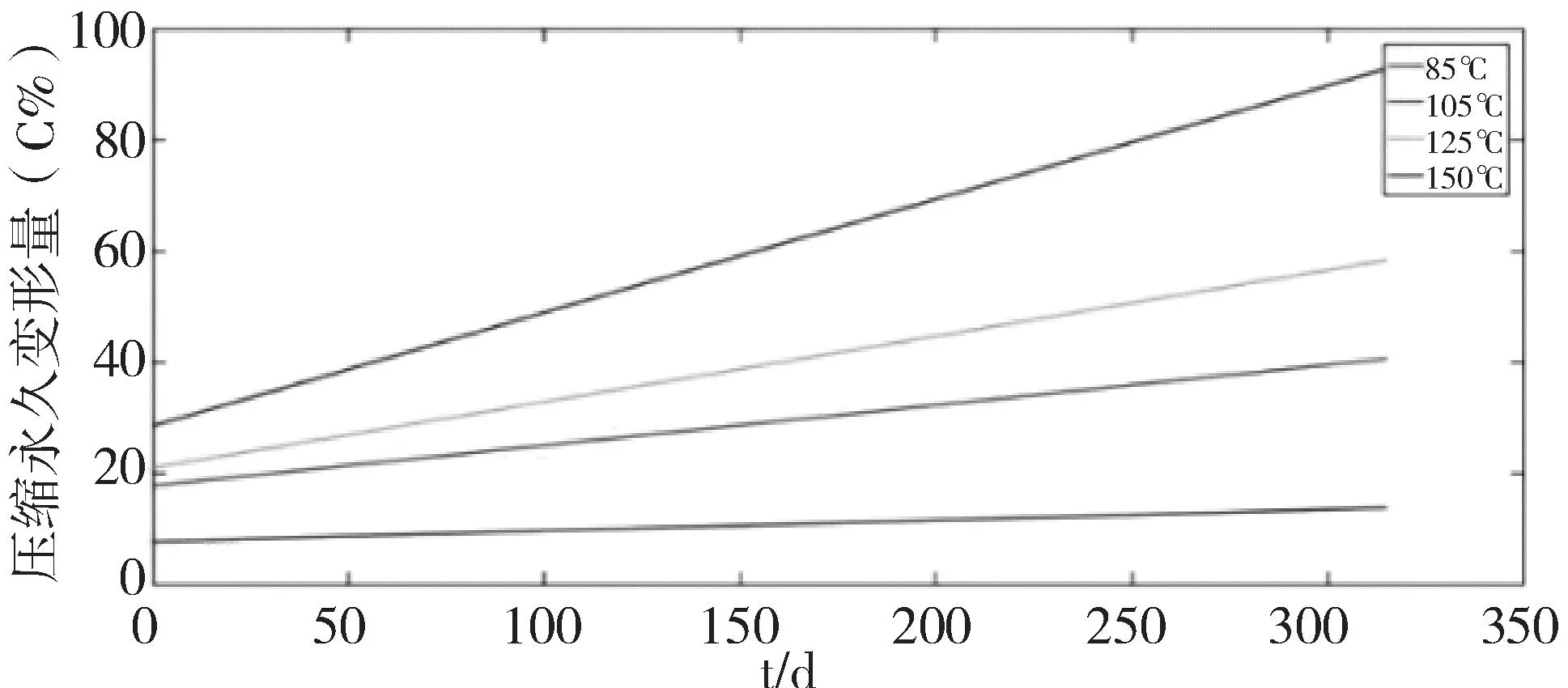
图6 实际压缩量时压缩永久变形率随老化时间变化拟合曲线

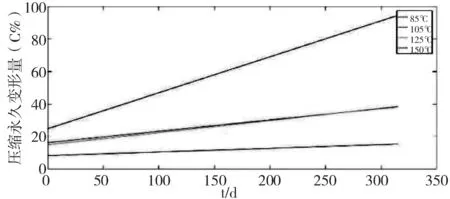
图7 最大压缩量时压缩永久变形率随老化时间变化拟合曲线

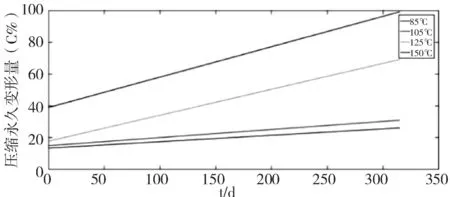
图8 最小压缩量时压缩永久变形率随老化时间变化拟合曲线

通过拟合后的曲线反推零时刻情况,发现所有曲线都没有过(0,0)的点,并且c0都要大于0。这表明橡胶在短时间(2.6d)内,橡胶样品的高温加速老化的机制与长时间内(>2.6d)的不同,从长时间压缩老化得到的参数不适用于极短时间内的情况,绝大多数情况下,初始时压缩永久变形的速率是要大于长时间后压缩永久变形的速率。

在线性拟合条件下,压缩永久变形量C随老化时间t的增长而线性上升,加速应力越大(即加速老化试验温度越高),压缩永久变形速率k越大。

由图6、7、8拟合可得到温度T与压缩永久变形速率k之间的关系曲线,如图9、10、11所示。图9、10、11中可见Lnk与1/T呈现良好的线性关系,拓展可得到常温下的压缩永久变形量的变化速率k,进而估算获得常温下达到压缩永久变形量阈值所需时间t。同时,由图9、10、11可得到活化能E实际压缩量=46.6J/mol、E最大压缩量=44.4J/mol、E最小压缩量=39.2kJ/mol,根据阿伦尼乌斯公式可知,活化能E越小,退化速率越大,预测的使用寿命越短。

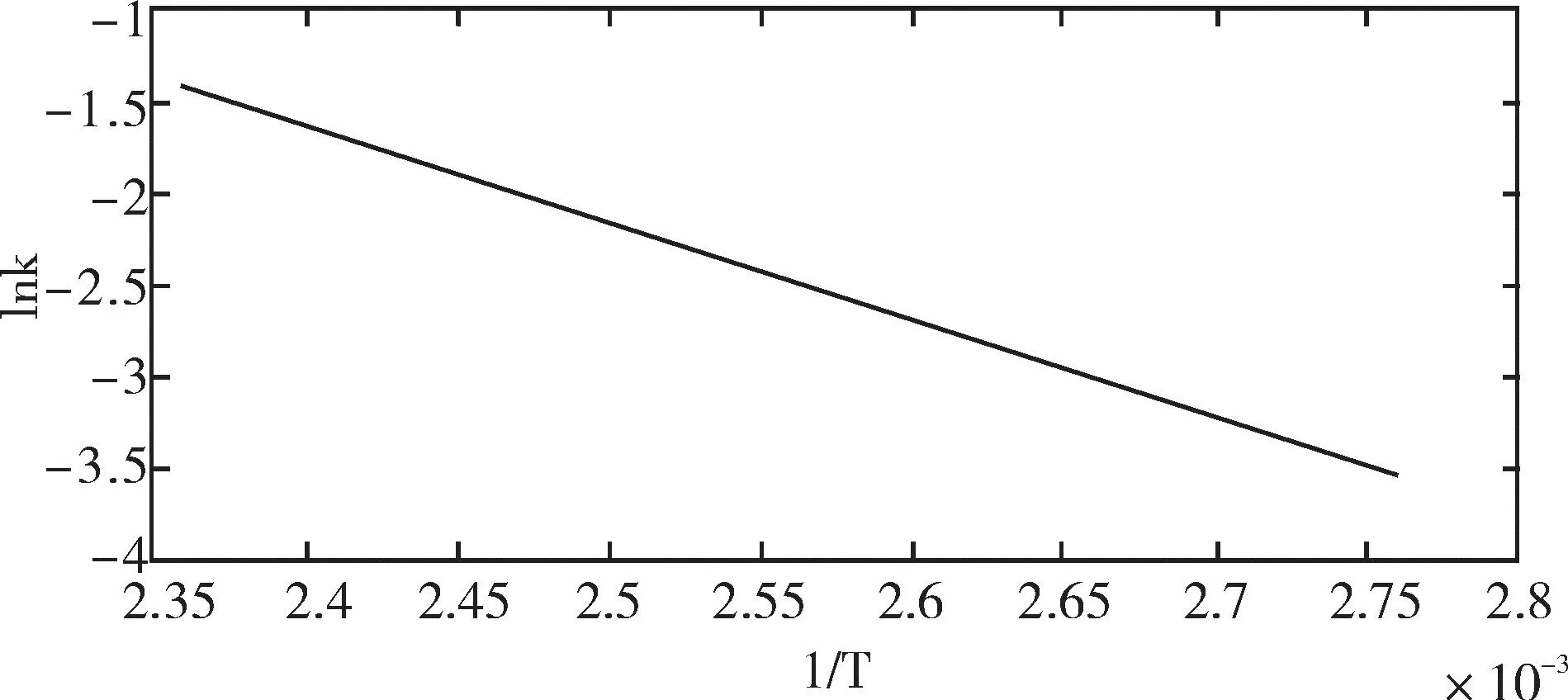
图9 实际压缩量时lnk与1/T的关系

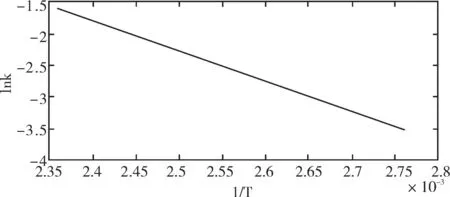
图10 最大压缩量时lnk与1/T的关系

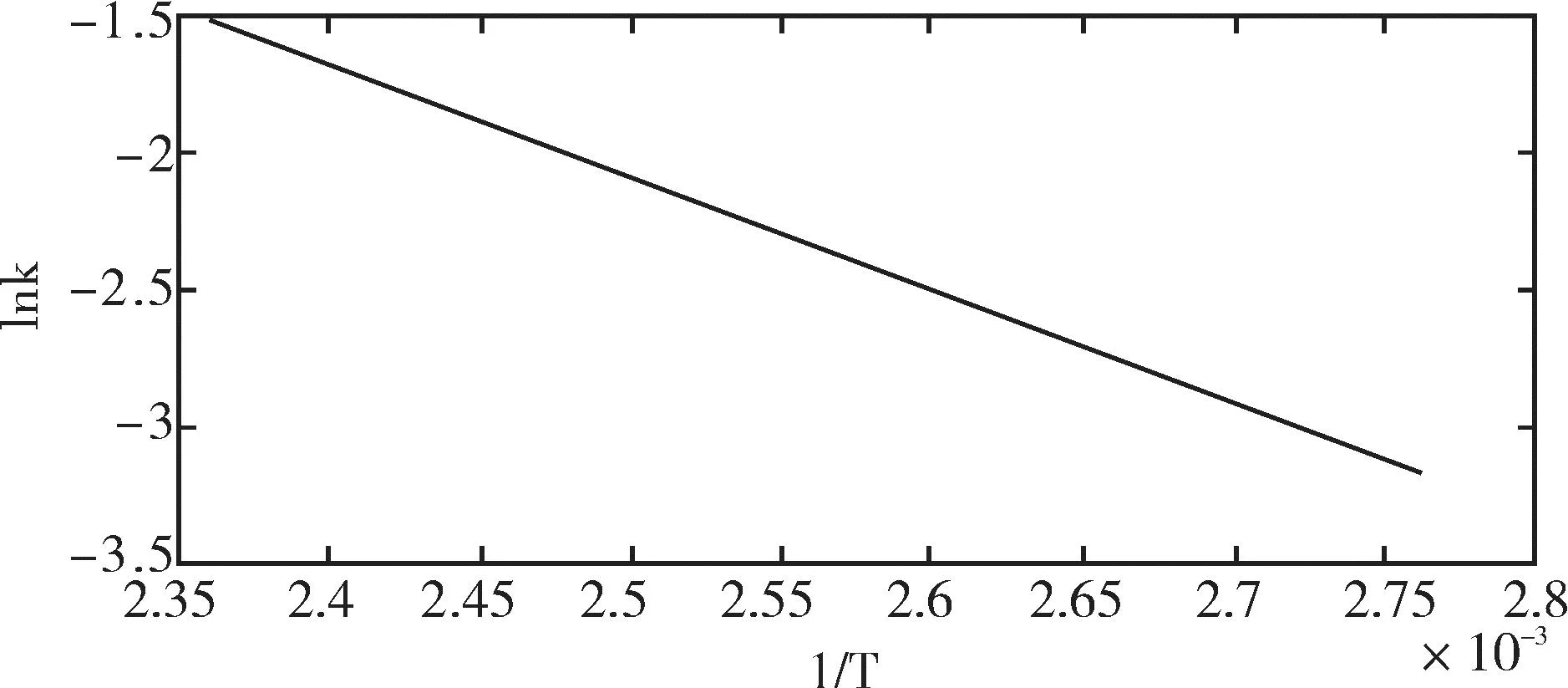
图11 最小压缩量时lnk与1/T的关系

由图9可以看出,Lnk与1/T呈极好的线性关系,根据该曲线可以计算出25℃情况下的k,在根据式3-2可以估测常温下橡胶件退化至失效阈值所需要的时间。

图9中得到的曲线表达式为:

Lnk=-5409×1/T+11.53

(4-1)

在应力水平25℃时,求橡胶件压缩永久变形速率:

T25=25+273.15=308.15

(4-2)

带入式4-1中,得到k25=0.0024,k25即为橡胶件在25℃时的压缩永久变形速率。

将式4-2简化为线性函数:

C=kT+C0

(4-3)

当C1=C2,并假设C0=0时:

C1=k1T1=C2=k2T2

(4-4)

则在温度为25℃、橡胶件退化至失效阈值(C=80%)时,

C25=k25T25+C0

(4-5)

80=0.0024T25

(4-6)

可以得到T25=33333d=91.3年,则根据动力学直线化法,实际压缩量橡胶件的预测寿命为91.3年。

同理可得,最大压缩量和最小压缩量橡胶件退化至失效阈值(C=80%)时,最大压缩量橡胶件的预测寿命为86.3年、最小压缩量橡胶件的预测寿命为46.3年。

4 结论

(1)橡胶件加速老化试验均遵循温度越高老化速率越快的规律。

(2)建立了连接器密封用橡胶件使用寿命的预测模型,计算出表观活化能E实际压缩量=46.6J/mol、E最大压缩量=44.4J/mol、E最小压缩量=39.2kJ/mol,在使用温度为25℃以及压缩永久变形率的失效阈值为80%时,实际压缩量橡胶件的预测寿命为91.3年、最大压缩量橡胶件的预测寿命为86.3年、最小压缩量橡胶件的预测寿命为46.3年。

(3)过大压缩量会导致O形橡胶圈使用寿命降低,主要原因为承受应力越大老化速率越快。过小压缩量也会导致O形橡胶圈使用寿命降低,主要原因为相同失效阈值所对应的压缩永久变形量允许范围变小。因此,压缩的大小要设计合理。