基于增量动力分析的建筑震害预测研究

庞倩文，翟永梅，胡 苇

（1.同济大学 土木工程学院，上海 200092；2.同济大学 上海防灾救灾研究所，上海 200092；3.同济大学 建筑与城市规划学院，上海 200092）

0 引言

目前广泛应用的建筑震害预测方法主要有三类：经验方法、半经验半理论方法和结构理论计算方法[1]。随着计算机技术的发展和有限元理论、弹塑性理论的进步，以增量动力分析（IDA）法为代表的建筑理论计算方法成为不同强度地震动作用下结构震害预测最有效的方法之一[2]。自1997年Bertero[3]提出增量动力分析的概念后，许多学者进行了后续的研究。2002年，Cornell[4]在总结前人研究的基础上提出了IDA 方法，并且给出了一种增量的方法——hunt&fill 点追踪算法，由此IDA方法在实际工程中得到应用[5-6]。在国内，2007 年，王朝波[7]利用IDA 方法对钢框架结构的弹塑性层间位移角进行了研究；2019 年，高龙[8]通过IDA 法研究了单跨框架结构在23 条地震波作用下的抗倒塌性能。然而，IDA 方法在震害矩阵的研究中应用还较少。2013 年，李葱葱，马东辉[9]等通过IDA 方法，建立了典型框架结构的震害矩阵。但是，上述文献均未说明选取的地震波条数对结果的影响，地震波条数较少无法保证计算结果的准确，地震波条数过多计算耗时。本研究综合考虑了结果的准确性和计算的高效性，研究当分布参数比较稳定时所需要的地震波条数，在此基础上，得到建筑的震害矩阵，为建筑的震害预测提供科学参考。

1 增量动力分析

增量动力分析方法是向结构模型输入一组或多组地震动记录，每一组地震动是由一条原始的地震动记录进行增量调幅所得。然后在这一组经过调幅的地震动作用下进行结构的弹塑性时程分析，得到一系列结构的弹塑性地震响应，产生一条或者多条损伤指标（Damage Measures DM）和地震动强度指标（Intensity Measures IM），之间的关系曲线，即IDA 曲线，按照一定的统计方法，可以评估结构的抗震性能。

IDA 方法的结果通常通过地震动强度指标和结构的损伤指标来进行描述，用以说明结构的响应随地震作用的增强而变化的趋势。目前适合IDA 方法的常用IM 指标有：地面峰值加速度（Peak Ground Acceleration，PGA）、地面峰值速度（Peak Ground Velocity，PGV）以及阻尼比为5%的结构基本周期对应的加速度谱值Sa（T1，5%）等。结构的损伤指标反映结构随某一地震动调幅系数的增大而变化的非负变量。一般选用最大层间位移角作为IDA 分析的结构损伤指标。

2 基于增量动力分析的震害预测方法

随着增量动力分析方法的提出，利用增量动力分析方法建立震害矩阵具有重要的研究价值，通过增量动力分析可以利用计算机和有限元方法在短时间内得到大量的计算结果，比传统先收集历史资料再进行分析的方法在效率上有巨大的提高；因为计算模型可以根据目标结构类型、特点进行建模，所以更加有针对性；利用增量动力分析可以针对一个结构输入大量不同的地震波，得到大量的结果有利于进行更加深入的挖掘和分析。

本文提出了一种基于增量动力分析结果建立震害矩阵的方法：首先计算每个地震强度指标IM（本文选用PGA）值处的不同地震波对应的震害损伤指标DM（本文选用最大层间位移角）数据；然后根据每个IM 值对应的DM 均值和标准差，即可求出其概率分布；最后结合各震害等级的最大层间位移角临界值，计算临界层间位移角的超越概率，从而得到震害矩阵。

3 算例：典型RC 框架结构基于增量动力分析的震害预测

3.1 结构体系介绍

本文算例为一个6 层钢筋混凝土框架结构，首层层高3.6 m，二层及以上层高均为3.3 m，总高度20.1 m，跨数为4×2，结构外形尺寸为8.4 m×16.8 m。采用C35混凝土，梁柱纵向钢筋采用HRB400。框架柱截面尺寸为550 mm×550 mm，框架梁截面尺寸为250 mm×600 mm。平面布置如图1（左）所示，在Etabs 中进行建模，模型如图1（右）所示。该结构位于上海市市区，抗震设防烈度7 度（0.1g），地震分组为第一组，场地类别为Ⅳ类，地面粗糙类别为C 类。楼板厚度取150 mm，楼面恒载（除自重）2.0 kN/m2，楼面活载2.0 kN/m2。本文所涉及的其他计算模型基本参数与本例类似。

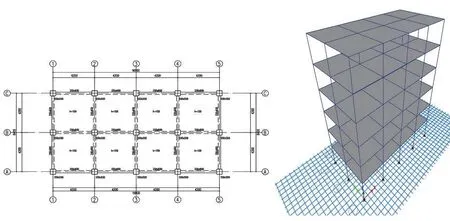
图1 结构平面布置图（左）和Etabs中的框架模型（右）Fig.1 Layout plan of structure（left）and framework model in Etabs（right）

3.2 增量动力分析

本文按如下规则在PEER 数据库中选取地震波：反应谱特性按照上海规范计算得出；持续时间大于15 秒，震源距离大于50 km，震级大于6.5 级，场地剪切波速取100 m/s～250 m/s。最终选取了25 条地震波作为输入。分别是《上海市建筑抗震设计规程》（DGJ08-9-2013）中建议给出的5条天然波及2条人工波，以及从PEER下载的100条天然波中按规则挑选出的18条。

对于大多数结构模型而言，实际完成一个IDA 分析得到一个几乎连续表示的IDA 曲线，需要花费大量时间，这使得人们考虑通过比例因子对地震波进行调整，可以花费较少的时间得到最终的结果。本文的研究目的是便于震害预测应用，建立震害矩阵，且烈度对应的PGA指标是指数型变化。为了方便对照的同时考虑每个烈度内相对均匀的分布，故采用变步长和等步长结合的方法进行调幅，即在不同范围采用不同步长，同一范围采用同样步长的方法对地震波进行调整。具体做法为：在PGA≤0.05 g时，增长步长为0.02 g；在0.05 g ＜PGA≤0.1 g时，增长步长为0.01 g；在0.1 g＜PGA≤0.2 g 时，增长步长为0.02 g；在PGA＞0.2 g 时，增长步长为0.04 g，最终将每一条原始地震波进行14 次调幅。PGA调整结果为：0.01 g、0.03 g、0.05 g、0.06 g、0.07 g、0.08 g、0.09 g、0.1 g、0.12 g、0.14 g、0.16 g、0.18 g、0.20 g、0.24 g。以PGA为IM进行增量动力分析，计算结果如图2所示。

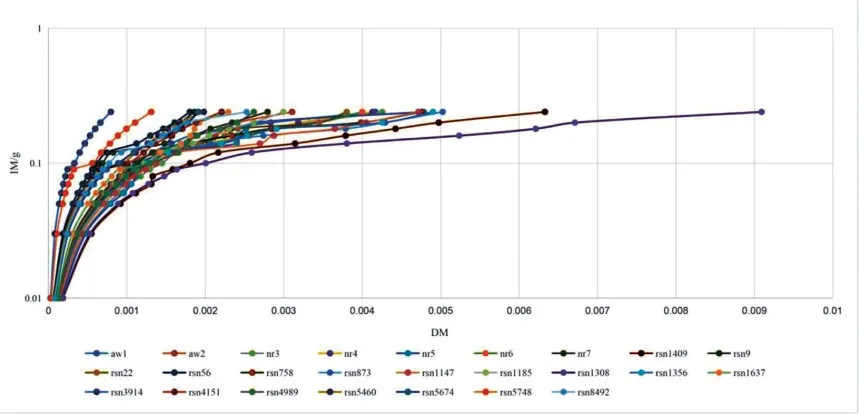
图2 25条地震波对应的增量动力分析结果Fig.2 Incremental dynamic analysis results of 25 seismic waves

利用SPSS 中的K-S 检验法对数据进行分布类型检验，各组数据的渐进显著性值基本大于0.05，因此样本近似为正态分布。

已有学者对震害等级与最大层间位移角的对应关系进行了研究，本研究综合马东辉等[10]及张桦[11]的研究成果，取其平均值，设定震害等级与最大层间位移角θmax的关系如表1所示。

表1 框架结构震害等级与层间位移角θ的关系

震害矩阵是描述群体建筑在某一强度地震作用下不同破坏状态概率分布的一个重要方法和分析地震损失的主要依据，是衡量城市或地区某一类建筑抗震能力的综合尺度。本文利用统计学的方法建立震害矩阵：（1）针对每一烈度背景，适当划分震害指数区间，并给出统计直方图。震害等级基本完好、轻微破坏、中等破坏、严重破坏和毁坏对应的震害指数范围分别为：0.00～0.10、0.10～0.30、0.30～0.55、0.55～0.85、0.85～1；（2）拟合统计数据，给出临界层间位移角的超越概率，如表2 所示；（3）计算每一震害等级区间内的概率，得到震害矩阵，如表3所示。

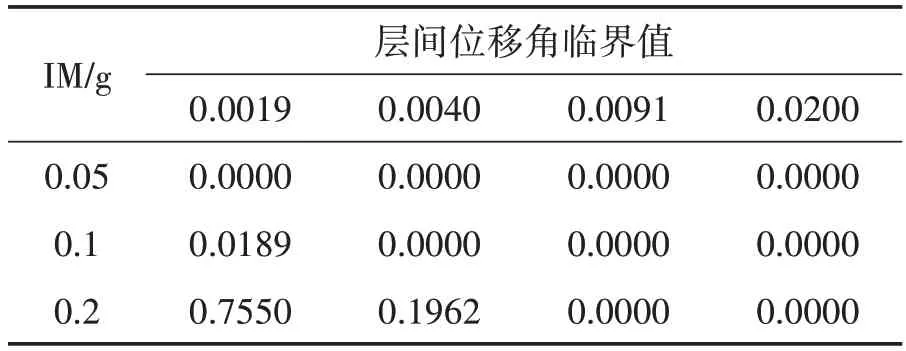
表2 临界层间位移角的超越概率

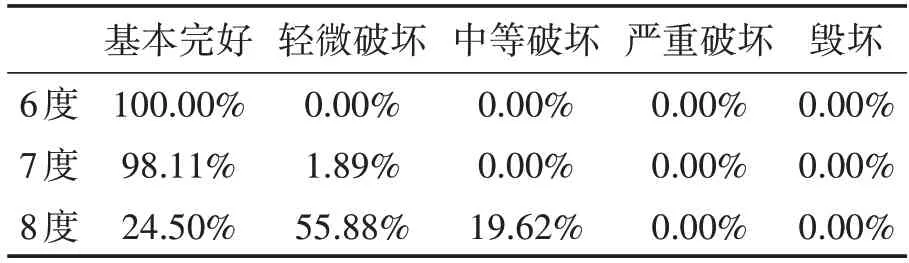
表3 震害矩阵

3.3 所需地震波数量的研究

对上述结构进行增量动力分析，结果表明，结构因输入地震波不同所造成的结构损伤指标是离散分布的。从上述25 条地震波中随机选波，进行不同数量的地震波输入，分别统计分布参数的均值和标准差，方法如下：（1）首先计算25条地震波在每个IM 增量处DM 值的均值和标准差，以此为标准；（2）随机挑选5 条、10 条、15 条、20 条地震波各10 组，分别计算每组地震波在每个IM 增量处DM 值的均值和标准差与第（1）步计算的25条地震波DM值的均值和标准差的相对偏差；（3）分别计算第（2）步中5 条、10 条、15 条、20 条的十组数据的DM 均值和标准差相对偏差的均值。最终得到每组随机抽取的地震波数量与相对偏差的关系，如图3所示。

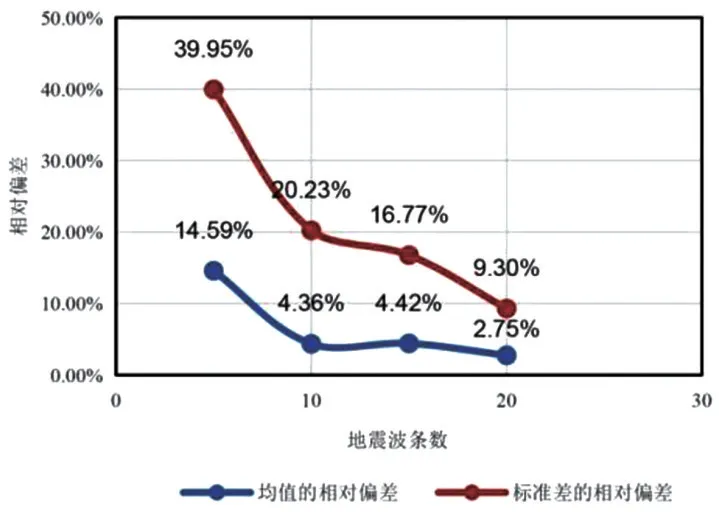
图3 地震波数量与计算结果相对偏差的关系Fig.3 Relationship between seismic wave number and relative deviation of result

由图3可以看出，当地震波条数由5条增加到10 条的时候，计算结果均值的相对偏差迅速由14.59%下降到4.36%，若再增加地震波条数，则均值的相对偏差下降的不明显，说明继续增加地震波条数对计算结果准确性的提升并不明显。而标准差的相对偏差也存在类似规律，但是标准差的相对偏差明显比均值要大。在得到震害矩阵的计算中，均值的重要性要大于标准差，所以作者认为，在一般应用中计算10 条地震波即可满足需要；而在做出比较精确的震害预测时，建议选取20条地震波。

因为时间有限，所以计算的总样本数较少，仅为25 条，计算结果基本可靠，将来的研究可以扩大样本数量至100 条甚至更多，将得到更加可靠的结果。

3.4 关于地震强度指标IM选择的研究

由图2 可以看出，增量动力分析计算结果中DM 层间位移角的离散度较大，不利于震害预测的应用。出现该情况的原因可能是地震动记录会存在某一些持续时间非常短但是加速度很大的峰值，这会在将峰值调整为1 的过程中使得其他部分的加速度相对调整得过小。阻尼比为5%的结构基本周期对应的加速度谱值Sa（T1，5%）调整方法可以有效的解决离散度过大的问题，但是这个方法的难点在于将加速度谱值与烈度对应。考虑到《上海市建筑抗震设计规程》（DGJ08-9-2013）中建议给出的5 条天然波及2 条人工波，本文的做法是：（1）将上海规范给出的7 条“标准波”进行调幅，并生成对应的反应谱，将其余地震波分别生成反应谱；（2）读取7条“标准波”对应反应谱的加速度谱值Sa（T1，5%），求出其均值；（3）将其他地震波的反应谱的加速度谱值Sa调整为上一步所求的均值；（4）利用第（3）步中的调整比例系数调整其他地震波的加速度值。

利用IDA 法再次计算上述经过调整的25 条地震波，计算结果对比如图4 所示。可以发现，用调整过的PGA作为IM的计算结果的标准差比直接以PGA作为IM时要小，离散度更低，而均值则有所增大，偏于安全，因此依照Sa调整过的PGA作为地震强度指标更适用于震害预测。

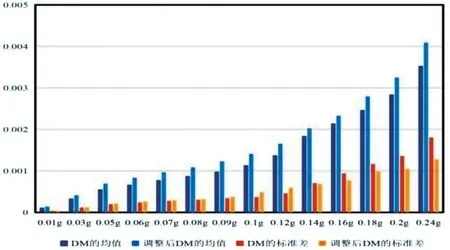
图4 两种IM指标对应的计算结果对比Fig.4 Comparison with the results of two different IM index

3.5 与其他文献震害矩阵计算结果对比

以调整过的PGA作为IM得到的震害矩阵与程显洲[12]等给出的上海地区震害矩阵和翟永梅[13]等得出的浦东新区潍坊街道的震害矩阵对比如表4所示。

为了便于对比分析和模拟抗震防灾规划决策，本研究中用震害指数来表征、比较建筑物总体的抗震性能水平。可以通过不同烈度下震害指数的大小，对比上述不同方法之间的差异。取基本完好、轻微破坏、中等破坏、严重破坏、毁坏对应的震害指数中值，分别为0、0.2、0.4、0.7、1.0，与震害矩阵中的概率相乘即可得到不同烈度下建筑的实际震害指数，如图5所示。

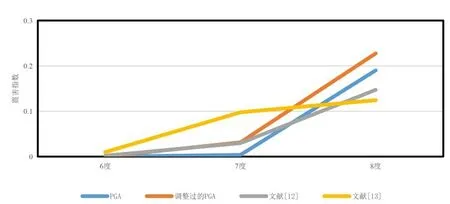
图5 不同研究得出的震害指数对比Fig.5 Comparison of seismic damage index from different research

可以看出，本研究利用IDA 得到的震害预测结果与参考文献的结果相差不大，震害指数的最大差值为0.0346，误差为3.5%，所以两种IM 的选择都是可行的。通过对比可以发现，以PGA 作为IM 在8 度的预测中与参考文献更为接近，震害指数差值为0.00084，误差为0.084%；以调整过的PGA 作为IM 则在7 度的预测中与参考文献更为接近，震害指数差值为0.01184，误差为1.184%。但是，以上建筑的震害矩阵并非是由针对同一区域尺度的研究得出，因此并没有考虑结构的随机性对震害预测结果的影响，这也是导致上述计算结果差异的主要原因之一。

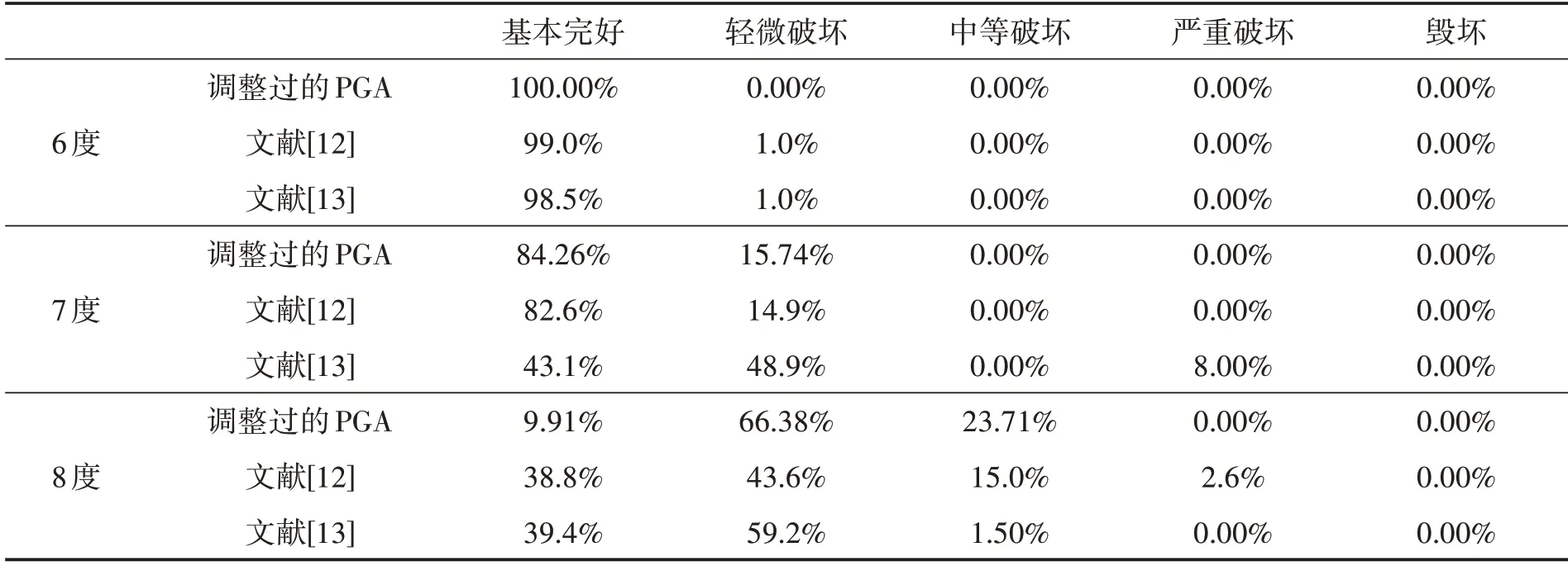
表4 不同研究得到的震害矩阵

4 结论

本文提出了基于增量动力分析（IDA）进行建筑震害预测的方法，研究了输入地震波条数和计算结果稳定性的关系，对比了两种不同的地震动强度参数的选取对结果的影响，得出下结论：

（1）增量动力分析中，选取10 条地震波进行分析就可以得出比较稳定的结果，如果对结果要求比较精确，推荐选取20条地震波进行计算；

（2）依照Sa调整过的PGA 作为地震强度指标得到的结果均值偏安全，标准差较小，所以依照Sa调整过的PGA 作为地震强度指标更加适合震害预测的应用；

（3）通过与其他学者研究得出的上海地区震害矩阵对比，结果基本一致。但是基于IDA的方法优势更为显著：在短时间内得到大量的计算结果，更加高效；根据目标结构进行建模，更加有针对性；

（4）基于增量动力分析方法得到震害矩阵的方法仍有一些不足之处，如：震害损伤指标的分布是否是正态分布并非是一个确定的结论，其他样本的适用性仍需后续研究结构的随机性包括结构布局的随机性、结构类型的随机性、建筑材料的随机性等，理想情况下应该全面的考虑这些因素，后续研究中有待进一步完善。