MPA-MMD方法在变转速齿轮箱振动信号特征提取中的应用

张 亢, 麻云娇, 袁志文, 陈向民, 田泽宇

(1. 长沙理工大学 能源与动力工程学院,长沙 410114;2. 华能国际电力股份有限公司 湖南清洁能源分公司,长沙 410015)

齿轮副在相互啮合时,齿面存在着复杂的接触载荷,容易导致齿面出现点蚀、剥落、裂纹等局部故障,影响着传动精度与设备安全。从齿轮箱振动信号中提取反映齿轮状态的故障特征,是判断与预测齿轮状态的关键[1-2]。然而,齿轮箱振动信号的多分量调制以及低信噪比特征,使得故障特征提取困难。其中关键的难点在于从低信噪比的振动信号中准确完整地分离出单分量调制信号。尤其是当齿轮箱运行在变转速工况时,其信号分量的时频特征会随转速的变化而变化,从而导致分量跨频带,以及不同分量发生重叠的现象。而目前广泛应用于非平稳多分量齿轮箱振动信号分解的方法,如经验模态分解、变分模态分解等,因为其是以时频局部时间尺度特征为分解依据的,所以并不能有效地分离[3-4]。因此,对于此类存在分量跨频带或交叉的信号分解,理论上不能以时间尺度特征作为分解依据。文献[5]提出了一种新的非平稳信号分解方法:多通道多分量分解(multichannel multicomponent decomposition,MMD)。MMD方法通过对多个传感器通道的信号求自相关矩阵,并进行特征值分解,得到一系列特征向量,因特征向量相互正交,则特征向量和信号分量可相互线性表示,也即每一个信号分量可由一组特征向量的线性组合表示,通过优化求得该线性组合的权值系数,便可得到相应的信号分量。一方面,多通道相比于单通道,能接收到更充分的设备信息量,可以在一定程度上消除采集故障信息的不确定性[6];另一方面,MMD没有以时间尺度特征作为分解依据,所以非常适合于分解变工况下分量交叉或跨频带的多分量齿轮箱振动信号。对于MMD法,决定分解效果最关键的是优化问题的求解,目前,MMD仅用于仿真信号的分析,优化过程采用的是最速下降 (steepest descent,SD)法直接寻优,因为仿真信号简单且信噪比高,可以取得较好的效果[7-9]。然而,对于实际的齿轮箱振动信号,由于存在大量噪声成分,SD算法无法快速准确地获得全局最优解,这便会直接影响MMD法的分解效果,从而影响后续故障特征的准确提取。因此,为将MMD法应用于齿轮箱振动信号等实际工程信号的分析,必须实现MMD法中优化问题的快速准确求解。

海洋捕食者算法(marine predators algorithm,MPA)[10]是一种新的群体智能优化算法,MPA算法相比于SD算法,理论上具有设计变量少、计算负担低、收敛速度快且能全局搜索获得最优解等优势,尤其是在噪声存在情况下可以在相关系数空间中更快更稳定地搜索全局最小值[11]。对此,为解决MMD方法在分析存在大量噪声的实际工程信号时,优化问题无法准确快速求解的缺陷,将MPA算法引入MMD方法,对其分解过程中的关键优化问题进行求解,进而提出一种基于MPA优化的MMD法(marine predators algorithm based MMD,MPA-MMD)。理论上,MPA-MMD相比于原MMD方法,更适合于分析受到噪声影响的实际齿轮箱振动信号。

综上,首先利用加噪仿真信号对不同优化算法的优化效果进行对比,以证明MPA-MMD方法较原MMD方法以及传统的基于时间尺度的分解方法的优势,在此基础上,利用MPA-MMD法分解变转速工况下具有跨频带或时频重叠特征的复杂齿轮箱振动信号,得到单分量的调制分量,进一步进行包络解调分析,来提取故障特征,为变转速工况齿轮故障特征提取提供一条新的途径。

1 MMD方法

MMD是一种新的不以时间尺度特征为分解依据的信号分解法,能够分解具有时频重叠和跨频带特征的多分量非平稳信号。具体步骤为如下所示。

步骤1假设多通道信号矩阵Xsen和多分量信号矩阵Xcom分别如下所示

Xsen=[x(1)(n),x(2)(n),…,x(G)(n)]T
Xcom=[x1(n),x2(n),…,xF(n)]T

(1)

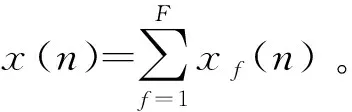
(2)

矩阵A的大小为G×F,存在秩rank(A)≤min{G,F},即独立通道数M=min{G,F},当且仅当G≥F时,独立通道数M=F,则一定存在F个独立分量。

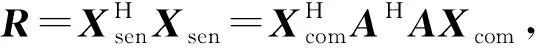
(3)

式中:ui为正交的特征向量;λi为特征值。

由式(3)知,ui为通道信号x(g)(n)的线性组合,而x(g)(n)为xf(n)的线性组合,所以ui可以写为信号分量xf(n)的线性组合

u1=α11x1+α21x2+…+αF1xF
u2=α12x1+α22x2+…+αF1xF
⋮
uM=α1Mx1+α2Mx2+…+αFMxF

(4)

当G≥F时,存在M=F个线性无关,信号分量xf(f=1,2,…,F)则可表示为特征向量ui的线性组合

xf=k1fu1+k2fu2+…+kFfuF

(5)

式中,kif(i,f=1,2,…,F)为未知权重系数。那么要得到相应的分量信号,就必须求出未知权重系数kif。

步骤3理论上每个信号分量都会在时频面上存在一个时频支撑域Df,而时频集中度越优,说明该支撑域包含的分量成分越集中,其他成分越少。目前,一般以时频分布的lp范数(0≤p≤1)作为时频集中度的度量指标,即

(6)

设每一个支撑域Df的面积为Df(f=1,2,…,F),那么当Df最小时,意味着对应的分量xf此时具有最佳的时频集中度。因此计算权重系数kif,变成了求解式(7)所示的关键优化问题,即

(7)

式中,γ1,γ2,…,γF为系数的寻优空间。

由于目前MMD仅用于简单仿真信号的分析,因此主要通过SD算法等直接寻优方式,直接从系数空间搜索出使式(7)的时频集中度最小的特征向量线性组合的权值系数kif,解决此优化问题。

(8)

2 MPA优化的MMD

对于MMD法,式(7)的优化问题的快速准确求解是决定分解效果的关键,而对于实际的工程信号,因为噪声的存在,简单的直接寻优方式可能会出现局部最优或无法快速收敛的问题,对此引入一种新型的智能优化算法MPA,解决MMD分析含噪工程信号时优化问题的快速准确求解。

2.1 MPA算法

MPA是一种基于群体的新型智能优化算法,捕食者通过平衡的Lévy和布朗随机觅食策略,获得最优的觅食效率。MPA的三段优化迭代基于猎物和捕食者不同的速度比,能很好的实现勘探到开发的过渡,使收敛更加快速稳定,此外由于引入了鱼类聚集装置(fish aggregation devices, FADs),从而可以避免停滞陷入局部最优,得到全局最优解。MPA算法的基本流程如下所示。

步骤1根据公式X0=Xmin+rand(Xmax-Xmin)初始化猎物矩阵Prey,rand(·)为[0,1]内的随机数,X0为初始值,Xmin和Xmax为变量的上下边界。

定义猎物矩阵Prey和捕食者矩阵Elite如式(9)所示。Prey和Elite的大小都是n×d,n为解的个数,d为维度。

(9)

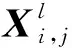
步骤2在系统大小一定的情况下,迭代根据猎物和捕食者的不同速度比(v=vprey/velite)分为3个阶段。在迭代初期(v≥10),猎物以布朗运动在解空间中进行勘探,评估新位置的适应度F,即食物丰富程度。如果新位置的适应度F更好,则更新Prey。

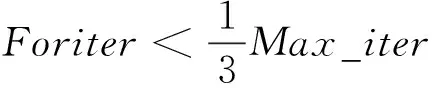
(10)

式中: ⊗为张量积;RB为包含布朗运动随机数的向量;stepsizei为步长;P=0.5固定;R为[0,1]中的均匀随机数的向量。

步骤3迭代中期(v=1),这一阶段猎物和捕食者都在找食物,一半种群进行勘探,一半种群进行开发。这一阶段猎物最佳策略是Lévy运动,而捕食者采用布朗策略。

产出导向法有三个核心环节(文秋芳，2015):一是“驱动”环节(motivating)，教师设计合适的交际场景和具有潜在交际价值”的任务，激发学生完成任务的热情，增强学习的动力;二是“促成”环节(enabling)，教师提供必要的输入材料，引导学生通过对听和读材料的选择和加工，获取完成任务所需的语言、内容、语篇结构等信息，促成产出任务的完成;三是“评价”环节(assessing)，即学生完成基本的产出任务或类似的新任务，教师做出即时评价和补救性教学。

前一半种群

stepsizei=RL⊗(Elitei-RL⊗Preyi)
Preyi=Preyi+P·R⊗stepsizei

(11)

后一半种群

stepsizei=RB⊗(RB⊗Elitei-Preyi)
Preyi=Elitei+P·CF⊗stepsizei

(12)

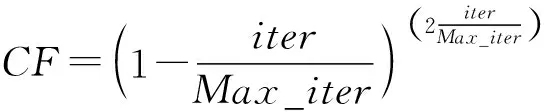
步骤4迭代后期(v=0.1),捕食者的最佳策略为Lévy运动开发策略,从而更有效地搜索特定区域。

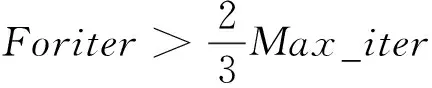
(13)

步骤5记忆当前成功觅食的位置,将当前迭代的所有解的适应度Fi与前一次迭代中的解的适应度Fi-1进行比较,如果当前的适应度F更小,则用当前解替换前一次迭代的解,更新Elite。

步骤6添加FADs更新Prey。FADs可以使捕食者进行较远的跳跃,从而避免停滞陷入局部最优。

(14)

式中:U为包含二进制数组的随机向量,如果数组小于0.2,它会将该数组置0,如果数组大于0.2,它会将该数组置1;一般设FADs的影响概率为PFADs=0.2;r为[0,1]中的均匀随机数; 下标“r1”和“r2”为猎物矩阵的随机索引。

2.2 MPA-MMD方法

利用MPA求解式(7)所示的优化问题,提出了基于MPA的MMD方法(MPA-MMD),具体优化求解过程如下所示。

根据式(5),设某个信号分量的表达式如式(15)所示,其中γf(f=1,2,…,F)为未知权重系数。

y=γ1u1+γ2u2+…+γFuF

(15)

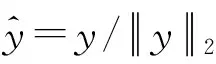
(16)

在条件γi=kii=1下,系数集γ1,γ2,…,γF为MPA算法的寻优空间,且因为MMD方法中需要将信号表示为复数形式,所以需要分别搜索其实部Re{γf}和虚部Im{γf},其中f=1,2,…,F,且f≠i。

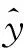
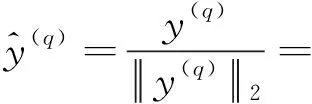
(17)

(18)

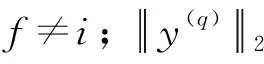
(19)

固定γi=1,则权值系数的搜索空间大小为2(F-1),系数取值范围为[-1,1]。通过MPA搜索得到的使适应度函数(18)最小化的系数组kfi如式(20)所示,此时给定解与期望最优解最接近。

(20)

将此时满足式(16)的系数组kfi=γf(f=1,2,…,F)代入式(15),即得到了基于MPA优化的一个信号分量。后续按照第1章MMD方法中的步骤4进行操作,便可产生下一轮迭代的信号,直至完成整个分解。

3 仿真信号分析

构造如式(21)所示的加噪仿真信号x(t),其由5个分量组成,σ(t)为叠加的白噪声信号,信噪比(signal-to-noise ratio,SNR)为-5 dB。其中:x1(t)和x5(t)为齿轮轮齿局部故障仿真分量;x2(t),x3(t)和x4(t)为跨频带线调频分量。仿真信号x(t)的STFT时频表示和提取的时频脊线,如图1所示。由图1(a)可知,信号各分量明显受到了噪声的影响,由图1(b)可知,信号分量具有跨频带和相互交叉的时频特征。

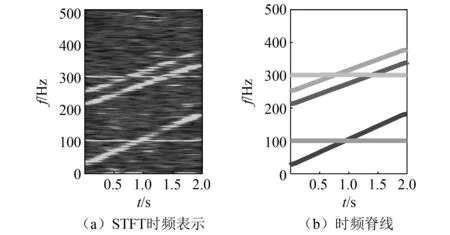
图1 仿真信号x(t)的STFT时频表示和时频脊线Fig.1 STFT time-frequency representation and time-frequency ridge for simulation signal x(t)

(21)

由MMD方法理论可知,信号的实际分量数可由其自相关矩阵的特征值分解得到的非零特征值的数量决定。加噪仿真信号x(t)的特征值分布图,如图2所示。由图2可知,非零特征值个数明显多于理论分量数,这正是因为噪声成分的存在,导致了非零特征值数量的增加,代表信号分量的前5个最大的非零特征值的幅值,明显大于代表噪声成分的其他非零特征值的幅值,因此,根据MMD方法中G≥F的条件,本次分解选取通道数G=18。对于仿真信号的分析,可通过设置信号的初相位在[0,2π]的均匀分布空间内随机取值,来扩展通道数,形成任意通道数量的多通道信号。在此基础上,利用MPA-MMD方法对仿真信号x(t)进行分解,分解结果如图3所示,可以看出在噪声存在的情况下,仿真信号中的各个分量都被完整地分解出来,未出现明显的失真现象,证明MPA-MMD能够分解分量跨频带和重叠的多分量信号。进一步计算分解前后各信号分量的rényi熵[13-14],以进行定量分析,计算结果如表1所示。由表1可知,MPA-MMD分解得到的各分量的rényi熵与原加噪分量的rényi熵变化规律一致,且明显小于原加噪分量的rényi熵,更接近未加噪分量的rényi熵,这说明MPA-MMD分解效果良好,同时具有一定的抑制噪声的能力。

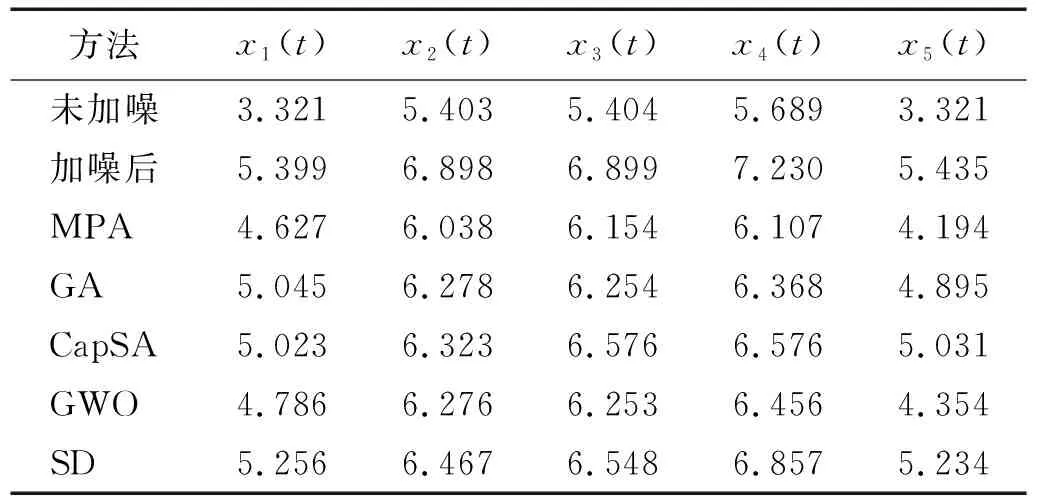
表1 仿真信号及基于各优化算法MMD分解结果的rényi熵Tab.1 rényi entropy of simulation signal and MMD decomposition results based on different optimization algorithms

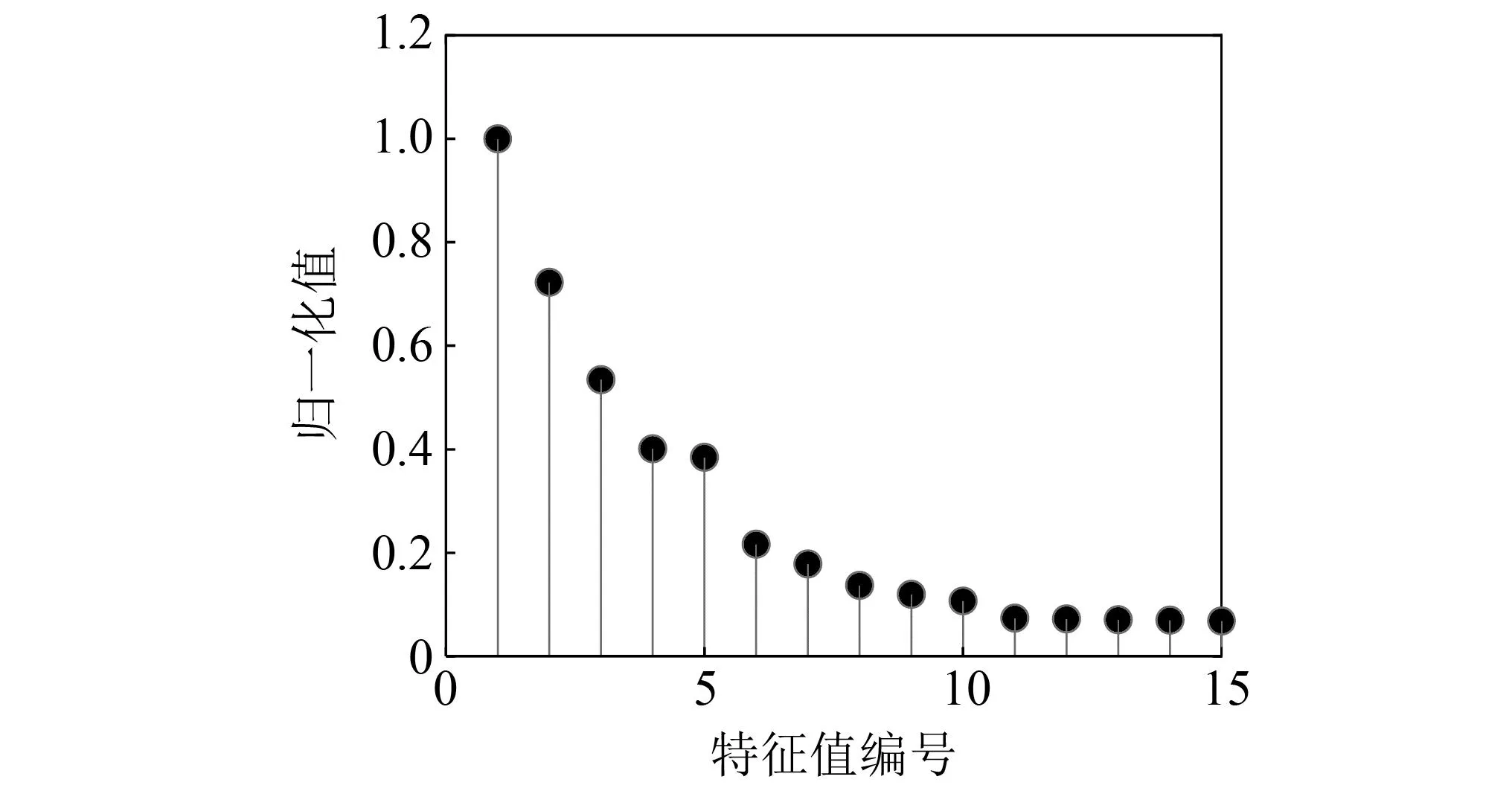
图2 自相关矩阵的特征值Fig.2 Eigenvalues of autocorrelation matrix

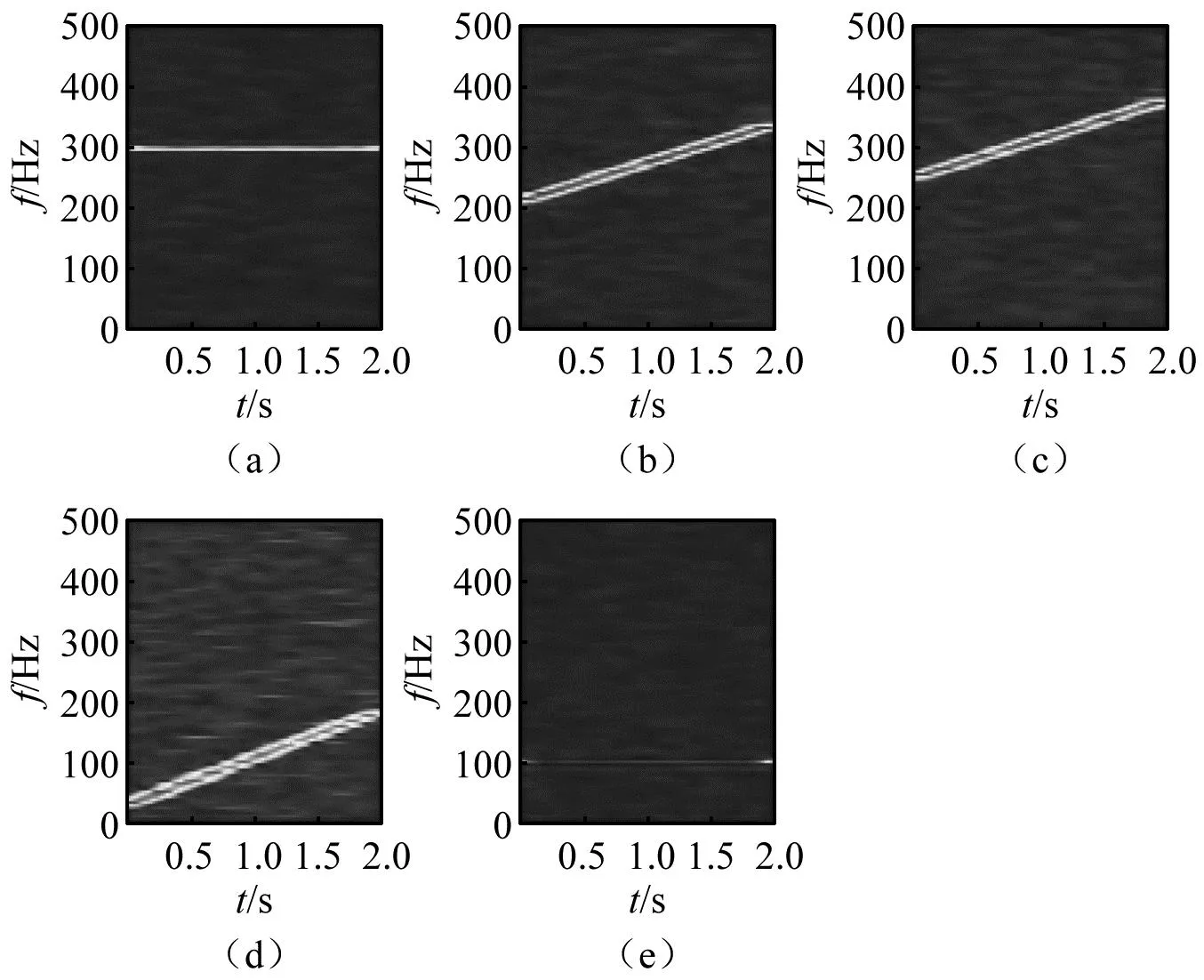
图3 仿真信号x(t)的MPA-MMD分解结果Fig.3 MPA-MMD decomposition results of simulation signal x(t)

将MPA算法与原MMD中的SD算法,以及目前常用的群体智能算法:遗传算法(genetic algorithm,GA)、灰狼优化算法(grey wolf optimization,GWO)和卷尾猴搜索算法(capuchin search algorithm,CapSA)分别作为MMD中优化问题的求解方法,对其寻优收敛情况进行对比分析。分析对象仍为式(21)所示仿真信号。分析过程中,设种群数为60,最大迭代次数为500,通道数G=18。为避免偶然性,每种优化算法都分别运行20次,各优化算法的20次平均迭代收敛曲线如图4所示。由图4可知,群体智能优化算法中基于MPA算法的适应度值最小,且收敛速度最快,而非群体智能优化算法的SD算法的适应度值明显大于群体智能优化算法的。根据MMD方法理论,适应度值即时频集中度值,是评价时频聚集性的定量标准,时频集中度值越小,时频聚集性越优[15-16],也即优化效果越好。进一步计算基于上述优化算法的MMD分解得到的分量信号的rényi熵,结果见表1。由表1可知,群体智能优化算法中基于MPA优化得到的分量信号的rényi熵最小,而直接寻优SD算法的rényi熵明显大于其他群体智能优化算法的rényi熵,这说明了基于MPA优化的MMD方法具有最佳的分解效果。

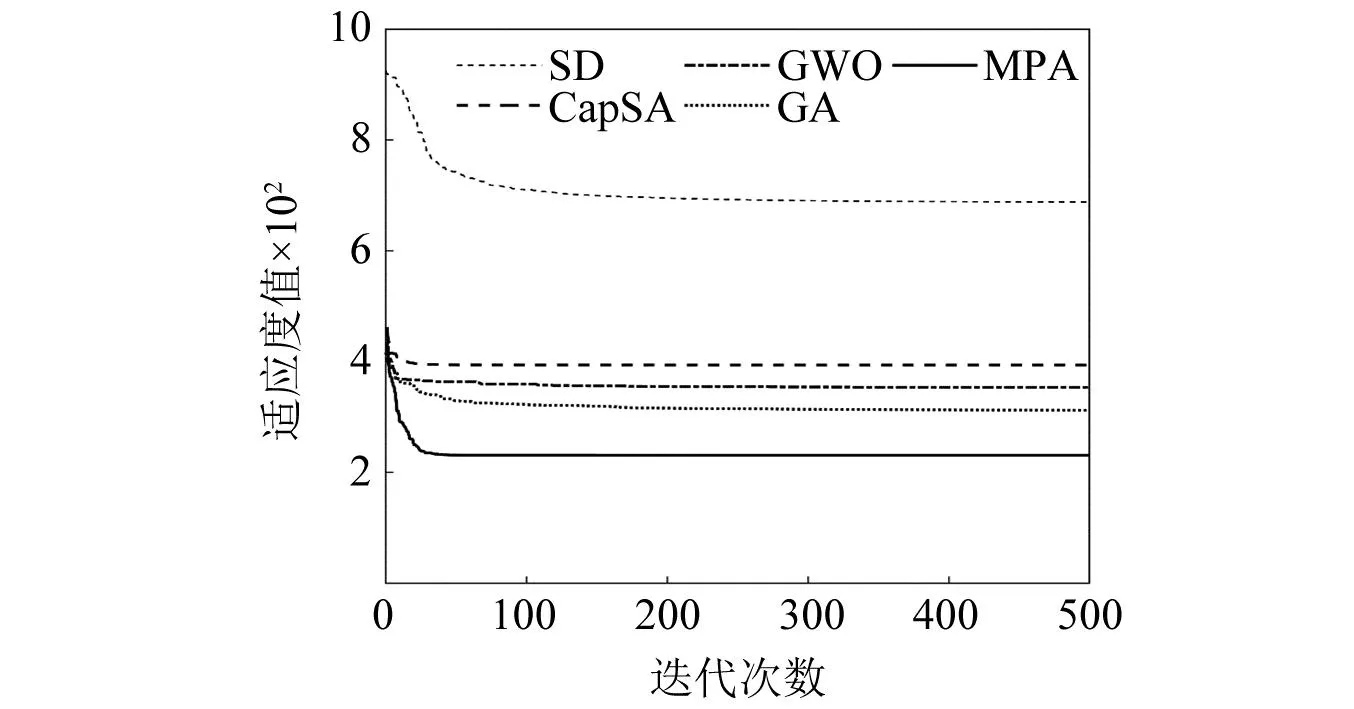
图4 各优化算法的迭代收敛曲线Fig.4 Iterative convergence curves of various optimization algorithms

为进一步对比,采用另一种基于局部时间尺度特征的多通道分析方法--多通道变分模式分解(multichannel variational mode decomposition,MVMD)[17],同样对式(21)所示的仿真信号进行分析。分解结果如图5所示。由图5可知,仿真信号从低频到高频被分解为了9个分量,超过了原信号所含分量数,并且由于MVMD仍然是以信号的局部时间尺度特征作为分解依据的,因此从图5(b)～图5(h)可知,跨频带分量x2(t),x3(t)和x4(t)被机械的分割到了不同的频段之中;而从图5(c)和图5(f)可知,虽然完整分解出了分量x1(t)和x5(t),但分量交叉的部分仍然存在交叉,并没有得到分离,这说明MVMD方法的分解结果出现了明显失真,失去了信号原有的物理意义,也进一步证明了MPA-MMD方法的优势。

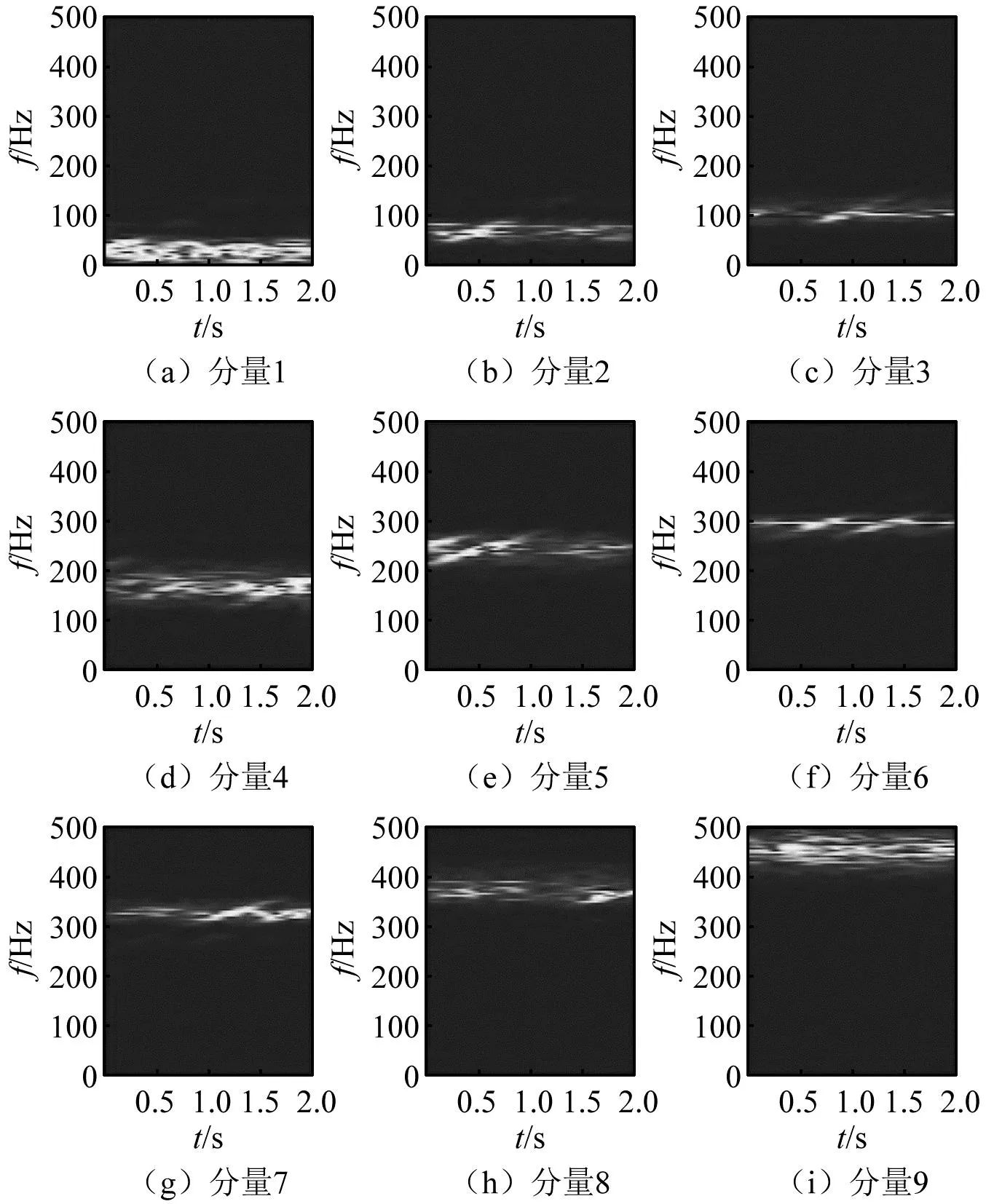
图5 仿真信号x(t)的MVMD分解结果Fig.5 MVMD decomposition results ofsimulation signal x(t)

实际设备中的齿轮箱,如风力机齿轮箱,其振动信号受工况和环境的影响,可能具有随机性和波动性的特征。对此设置如式(22)所示的具有波动性的加噪重叠多分量信号s(t),其由一个波动分量s1(t)和齿轮局部故障分量s2(t),以及白噪声σ(t)组成,SNR=-5 dB。s(t)的STFT时频表示如图6(a)所示。由图6(a)可知,s(t)存在明显的波动性与分量重叠特征。采用MPA-MMD方法对s(t)进行分解,通道数设为8,分解结果如图6(b)和图6(c)所示。由图6(b)和图6(c)可知,相互重叠的波动性分量与故障分量得到了很好的分离。计算两个分量分解前后的rényi熵,结果如表2所示。由表2可知,对于具有波动性的重叠信号,经MPA-MMD分解后,两个分量的rényi熵分别由7.300 2和8.135 5降到了5.712 4和4.074 2,且与未加噪分量的rényi熵接近,说明噪声得到了明显抑制。

表2 仿真信号s(t)及其MPA-MMD分解结果的rényi熵Tab.2 rényi entropy of simulation signal s(t) and its MPA-MMD decomposition results

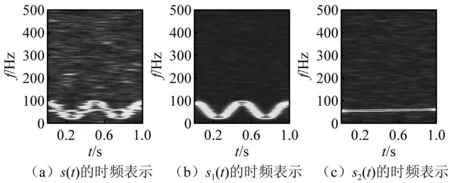
图6 仿真信号s(t)及其MPA-MMD分解结果Fig.6 Simulation signal s(t) and its MPA-MMD decomposition results

(22)

4 变转速工况齿轮箱振动信号特征提取

为了考察MPA-MMD方法对变转速工况下含噪齿轮箱振动信号的分析效果,在Spectra Quest公司的风力涡轮机动力传动系统故障试验台上进行两组齿轮故障振动信号采集试验,该试验台包含一个二级定轴齿轮箱和一个一级行星齿轮箱,驱动电机直接驱动定轴齿轮箱输入轴旋转,如图7所示。一组试验在定轴齿轮箱输入级的主动齿轮上设置了齿面磨损故障,以及在输出级的主动齿轮上设置了断齿故障;另一组将定轴齿轮箱中的断齿齿轮替换为同型号的正常齿轮进行试验。两个故障齿轮如图8所示。定轴齿轮箱参数及故障特征阶次,如表3所示。试验中,通过西门子公司的LMS多通道振动噪声测试系统进行振动数据采集与预处理。

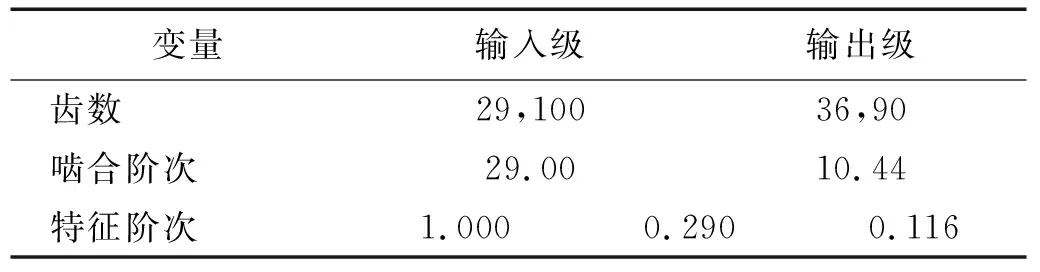
表3 定轴齿轮箱参数及特征阶次Tab.3 Fixed axis gearbox parameters and characteristic orders

图7 风力涡轮机动力传动系统故障试验台Fig.7 Wind turbine power transmission system faultstest bench

图8 故障齿轮件Fig.8 Faulty gears

试验1:在定轴齿轮箱箱体上布置5个PCB三轴振动加速度传感器,即通道数G=15,进行定轴齿轮箱振动数据采集试验。试验中,设置采样频率为4 096 Hz,采样时长为15 s,调节驱动电机转速从540 r/min增速到3 228 r/min。其中一个通道的振动信号时域波形及转速-时间曲线,如图9所示。由图9可知,信号的STFT时频表示如图10(a)所示,可以看出因为转速大幅度变化,导致时频图中主要存在着3个频率跨度很大的分量。考虑计算量以及方法运用的必要条件,利用MPA-MMD方法对其中8个通道的7～13 s时间段的数据进行分解,得到前两个分量的STFT时频表示分别如图10(b)和图10(c)所示。由图10(b)和图10(c)可知,跨频带分量直接得到了很好地分离,信噪比也明显提升。分别对MPA-MMD分解所得的分量信号进行阶次谱分析,结果如图11所示。由图11可知,在阶次10.44和29处存在明显谱线,分别对应了定轴齿轮箱中输入与输出级的啮合振动成分,且两边存在着明显的不对称的调制边频带。为明确边频带特征,进一步进行包络阶次分析,结果如图12所示。由图12可知,图12(a)中在阶次0.291 2处存在明显谱线,而图12(b)中在阶次0.993 1处存在明显谱线,这正好与故障齿轮所在转轴的转频阶次相近,符合试验工况,验证了方法的有效性。

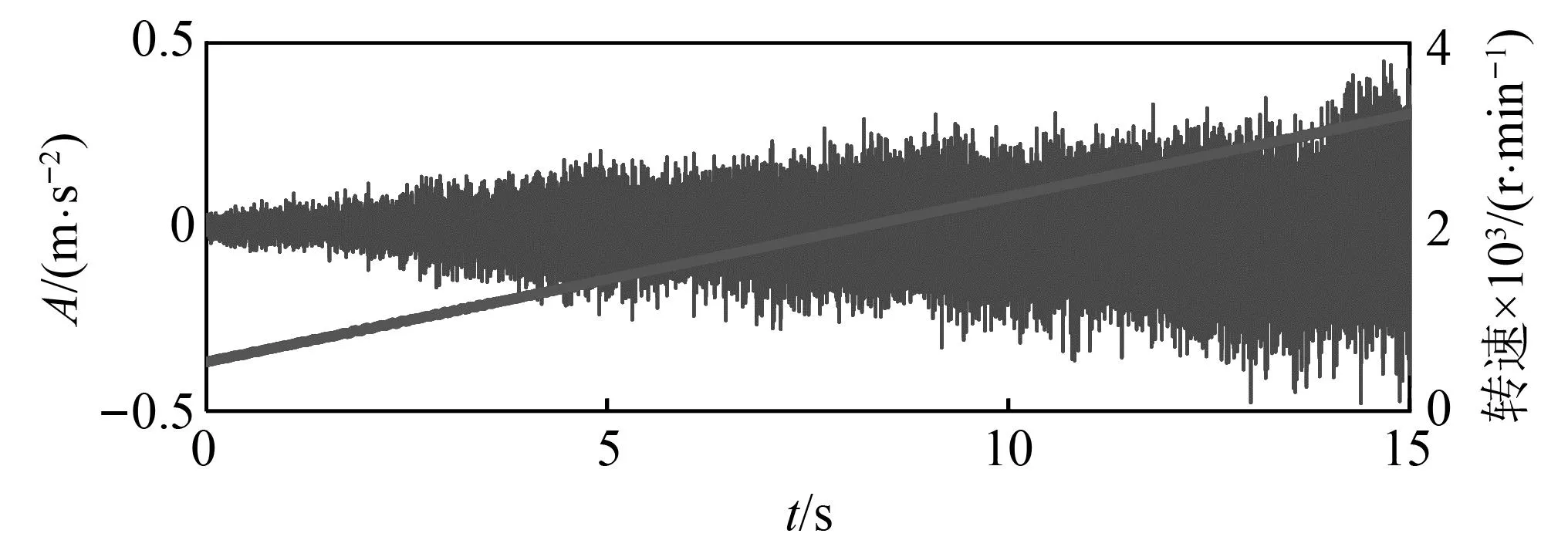
图9 某通道时域信号和输入轴瞬时转速(试验1)Fig.9 Time-domain signal of a channel and instantaneous rotating speed of input shaft (test 1)

图10 试验1所测数据的MPA-MMD分解结果Fig.10 MPA-MMD decomposition results of the data measured in test 1

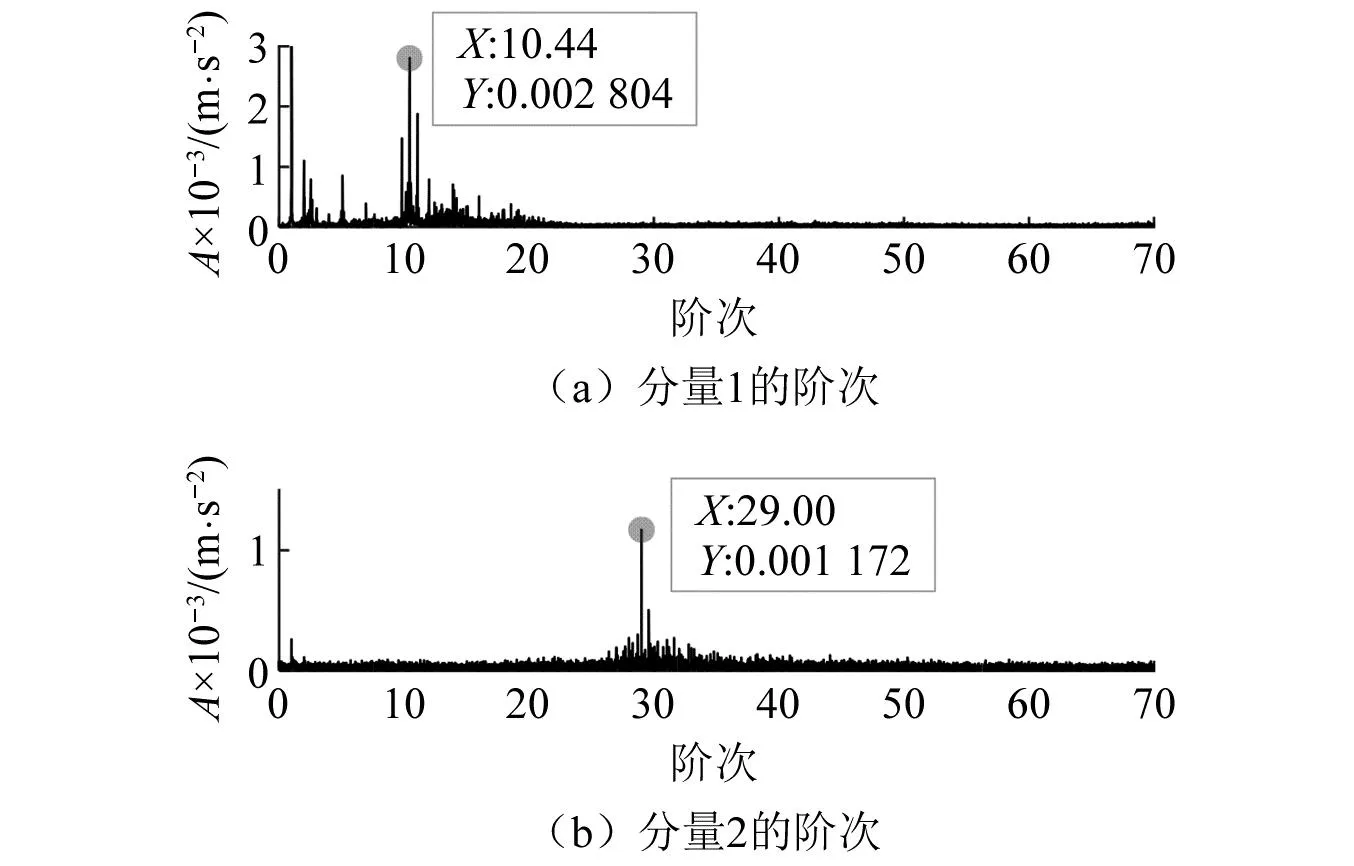
图11 分量1和分量2的阶次谱Fig.11 Order spectra of components 1 and 2

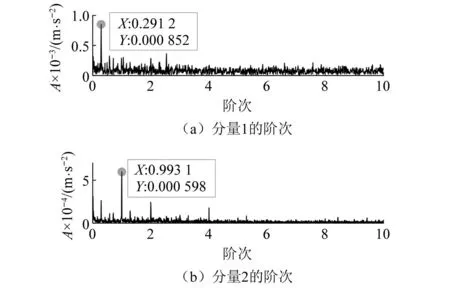
图12 分量1和分量2的包络阶次谱Fig.12 Envelope order spectra of components 1 and 2

直接对图9所示原始振动信号及其包络信号作阶次谱分析,结果分别如图13和图14所示。从图13中虽然可以找到输入级和输出级的啮合阶次谱线,但由于受到噪声的影响,其边频带不清晰,尤其是输出级啮合阶次的边频带,已经完全被噪声湮没;而图14中,也只能找到磨损齿轮所在转轴的1阶转频阶次,这未能反映出输入级和输出级齿轮都存在故障的真实情况。经过以上对比分析,进一步说明了MPA-MMD分解的必要性及其效果。

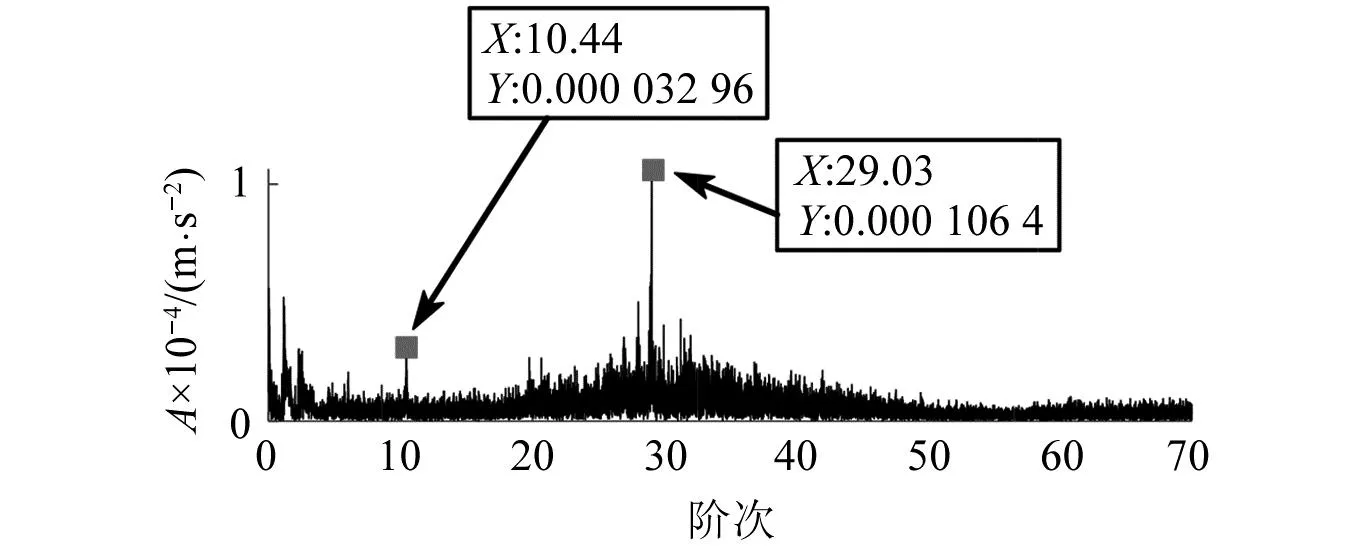
图13 图9所示信号的阶次谱Fig.13 Order spectrum of signal shown in Fig.9

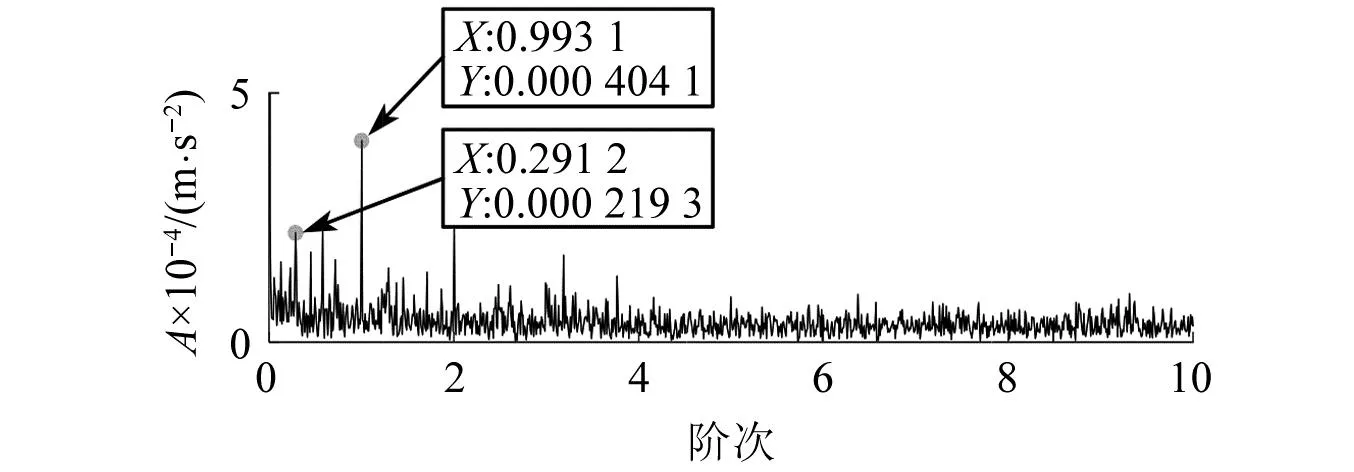
图14 图9所示信号的包络阶次谱Fig.14 Envelope order spectrum of signal shown in Fig.9

试验2:将试验1中的断齿齿轮换成同型号的正常齿轮进行第2组试验。试验中,设置采样频率为4 096 Hz,采样时长为15 s,调节输入轴转速从534 r/min增速到3 224 r/min。其中一个通道的振动信号时域波形及输入轴瞬时转速曲线,如图15所示。从图16(a)的STFT时频图可以看出被测数据中存在着两个频率跨度很大的分量,分别对应了输入级和输出级齿轮啮合振动分量,其中对应输入级齿轮啮合振动分量的能量明显大于输出级齿轮啮合振动分量的能量,且两跨频带分量多处与齿轮箱中固有振动成分及电干扰成分等恒定频率分量发生了交叉;图16(b)为其中一处分量交叉部位的局部放大图,可见特征复杂。利用MPA-MMD方法对其中10个通道的7～13 s时间段的数据进行分解,得到的前两个分量的STFT时频表示分别如图17(a)和17(b)所示,可以看出代表两级啮合振动成分的跨频带分量被分离开来,且与其交叉的成分以及噪声也得到了明显的改善。对分解所得的两个分量信号进行阶次谱分析,结果如图18所示。由图18可知,在图18(a)中虽然存在着对应了输出级齿轮啮合振动的10.44阶次谱线,但其两边的调制边频带不明显,符合正常齿轮啮合振动特征;而在图18(b)中,输入级齿轮啮合振动阶次29及其2倍频59.42处存在明显谱线,且两边都存在着较明显的调制边频带。进一步进行包络阶次分析,输出级和输入级齿轮啮合振动分量的包络阶次谱分别如图19(a)和图19(b)所示,可以看出图19(a)中无相应故障阶次谱线,而图19(b)中在阶次0.997 1及其倍频处存在明显谱线,这符合试验2时齿轮箱的状态特征,说明了方法的有效性。

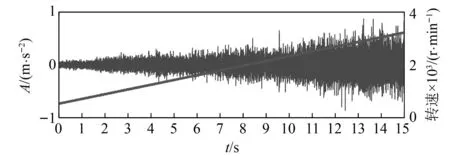
图15 某通道时域信号和输入轴瞬时转速(试验2)Fig.15 Time-domain signal of a channel and instantaneous rotating speed of input shaft (test 2)

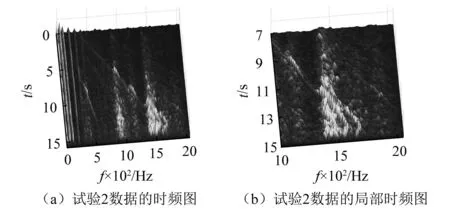
图16 试验2所测数据的STFT时频图Fig.16 STFT time-frequency plot of the data measured intest 2

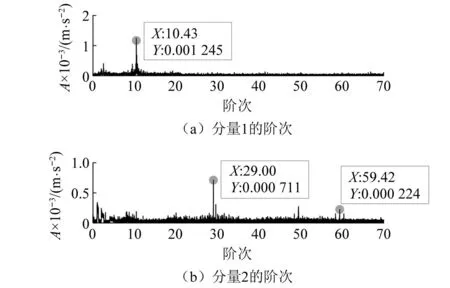
图18 分量1和分量2的阶次谱Fig.18 Order spectra of components 1 and 2

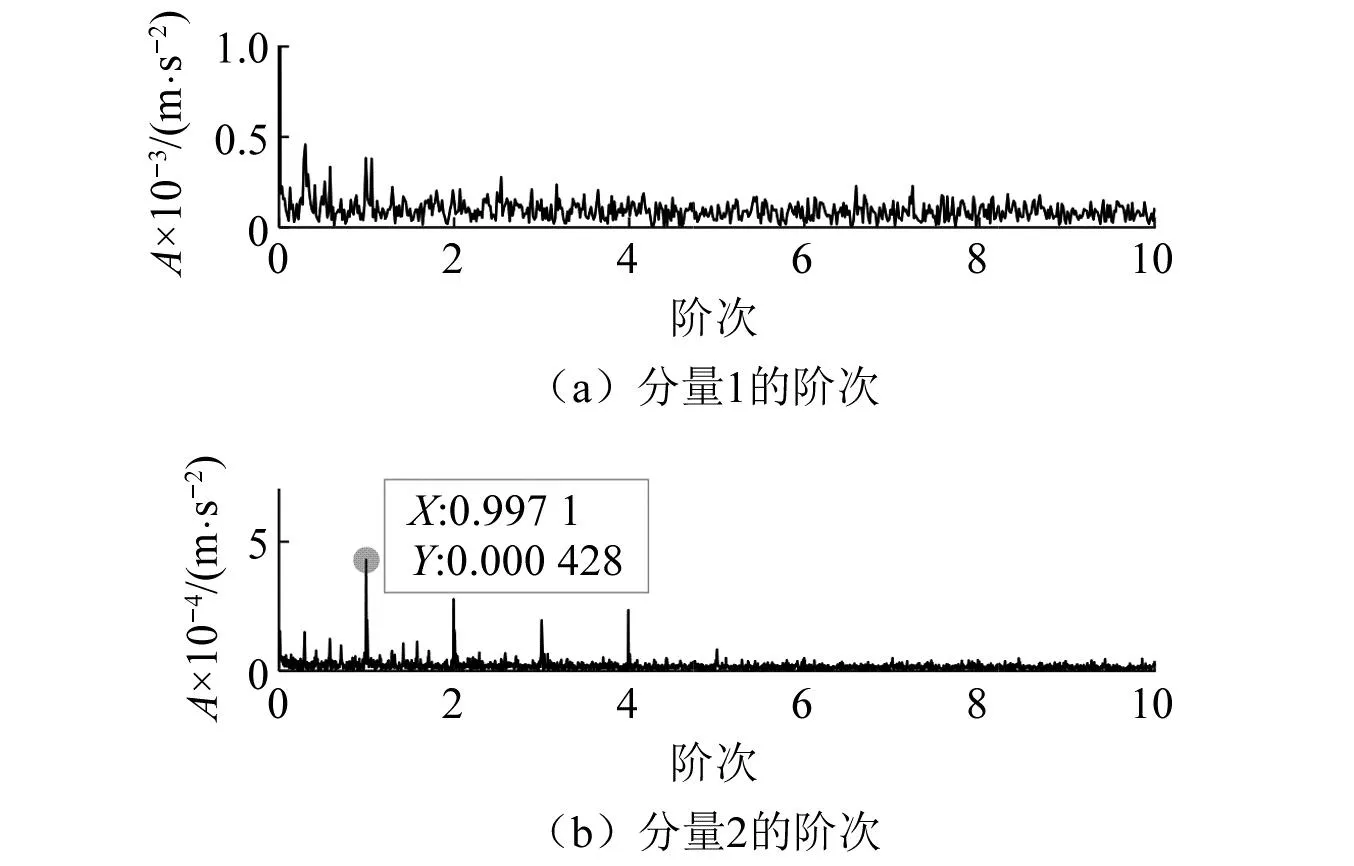
图19 分量1和分量2的包络阶次谱Fig.19 Envelope order spectra of components 1 and 2

5 结 论

本文利用MPA算法求解MMD方法中的优化问题,解决原MMD方法中直接寻优方式在分析实际含噪工程信号时的缺陷,进而提出MPA-MMD方法,并将其应用于变转速工况下齿轮箱振动信号的故障特征提取,得出了以下结论:

(1) MPA相比于原MMD方法中的SD方式,由于引入了FADs,可避免出现局部最优的问题,即求得的特征向量的线性组合的加权系数为全局最优,从而获得的信号分量在理论上具有最优的时频聚集性。

(2) 通过对加噪仿真信号的分析表明,相比于其他经典优化算法,MPA在收敛性和抑噪性方面具有优势;相比于以时间尺度为分解依据的MVMD,MPA-MMD对于呈现跨频带及时频重叠特征的复杂多分量信号,具有明显优势。

(3) 通过对变转速齿轮箱振动信号的分析表明,MPA-MMD不但能直接分解出受转速影响的跨频带故障分量,而且能将与其重叠的固有振动成分等恒频成分有效分离,为复杂齿轮箱振动信号的特征提取提供了新的有效方式。