波浪-地震联合作用下高速铁路跨海斜拉桥车桥耦合振动研究

雷虎军, 林镇荣, 温家生, 邱官发, 陈希茂

(1. 福建理工大学 土木工程学院,福州 350118;2. 中铁二十四局集团福建铁路建设有限公司,福州 350013)

随着我国高速铁路建设从陆地逐渐延伸到海洋,跨海桥梁已成为高速铁路线路的重要组成部分,其中桥上列车的行车安全问题倍受关注。在以往研究中,研究者更多关注高速铁路跨海桥梁在风、波浪以及风浪联合作用下桥上列车的行车安全问题[1-4]。相比普通桥梁,跨海桥梁面临深水环境,会长期受到波浪力的作用,且一旦发生地震,在桥梁下部结构还会产生附加动水压力[5]。由于我国地处环太平洋地震带与欧亚地震带间,地震发生频率高、强度大、分布广,高速铁路跨海桥梁遭遇波浪力、地震力以及地震附加动水压力同时作用的几率很大,其行车安全问题需考虑波浪-地震的联合作用。

关于波浪-地震联合作用下高速铁路跨海桥梁的行车安全性研究,首先应清楚波浪力和地震附加动水压力的模拟方法。关于波浪力的模拟,Morison等[6]首先提出采用Morsion方程计算小直径桩柱上的波浪力,由于其形式简单、物理意义明确,在工程界和学术界得到了广泛应用。然而,对于大直径桩柱,波浪的绕射现象不能忽略,此时应采用波浪的绕射理论求解[7]。对于跨海桥梁的下部结构,通常包括桥墩和群桩基础。目前分析群桩上波浪力的主要方法有两种:一是利用Morsion方程和群桩的附加动水压力系数直接计算桩柱上的波浪力[8];二是利用单桩上的波浪力乘以相应的群桩系数计算桩柱上的波浪力[9]。在波浪力的具体输入方面,房忱等、李永乐等、刘高等、崔圣爱等的研究在车桥系统中基于JTS 145-2015《港口与航道水文规范》[10]将每个墩位的波浪力简化为一个集中力并按三角函数输入。这种模拟方法可大大简化波浪荷载的输入,但由于跨海桥梁下部结构的桩柱众多,简化为一个集中力后其作用点的位置确定较困难,且忽略了各个桩柱的波坡面效应。地震作用下桥墩在水中运动导致水体对桥墩产生地震附加动水压力属于辐射波浪问题,且桥墩与其接触的流体间存在耦合作用。关于地震的附加动水压力,目前主要有两种考虑方法:附加质量法[11]和有限元法[12]。关于附加质量法,研究者主要采用简化或改进的Morsion方程来表述水体对桥梁结构的附加动水压力作用。关于有限元法,是利用流固耦合的基本理论,采用通用有限元程序建立精细化模型,研究结构在附加动水压力下的动力响应。利用精细化有限元模型可以与附加质量法进行相互验证,达到修正或改进计算精度的目的。

由于车桥系统的复杂性,本文在以往研究的基础上,根据线性波浪理论和Morsion方程按分布力模式输入波浪力,同时利用附加质量法考虑地震附加动水压力,建立波浪-地震联合作用下的列车-轨道-桥梁耦合振动分析模型。在此基础上,以某典型高速铁路跨海斜拉桥为例,输入桥位处的波浪参数和典型地震波,系统研究了波浪参数、地震动参数对该桥的动力响应及桥上列车行车安全性的影响,研究成果可为高速铁路跨海斜拉桥的设计提供技术支撑。

1 波浪-地震联合作用分析方法

1.1 动力学模型

波浪-地震联合作用下的列车-轨道-桥梁耦合振动模型,是在原有地震-列车-轨道-桥梁耦合振动模型[13]的基础上通过添加波浪力和地震附加动力压水模块实现的,耦合振动示意如图1所示。其动力方程可统一表达为

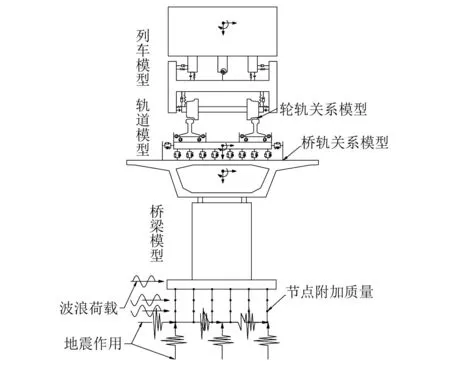
图1 耦合振动模型Fig.1 Coupled vibration model

(1)

(2)

(3)

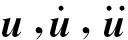
详细的列车、轨道和桥梁运动方程及其相互作用力推导、列车-轨道-桥梁-地震分析程序验证可参考文献[14],联立求解式(1)～式(3)即可得到波浪-地震联合作用下跨海桥梁-列车系统的耦合振动响应。仅介绍本文新增的波浪力P和地震附加动水压力fw的计算方法。

1.2 波浪力

本文的波浪力基于线性波浪理论和Morsion方程,参考JTS 145-2015《港口与航道水文规范》计算。对于小尺寸桩(柱),当D/L<0.2时,H/d≤0.2且d/L≥0.2或当H/d>0.2且d/L≥0.35时,作用在水底面以上高度z处柱体全断面上与波向平行的波浪力按下列公式计算

P=PD+PI

(4)

(5)

(6)

(7)

(8)

式中:L,H,d分别为波长、波高和水深;T为波浪周期;D,A为桩柱的直径和面积;γ为水的重度,取9.806 kN/m3;g为重力加速度;PD,PI为波浪力的速度分力和惯性分力;u,∂u/∂t为水质点运动的水平速度和水平加速度;CD,CM为速度力系数和惯性力系数;ω为波浪运动的圆频率;t为时间;y为波浪力输入的横向参考坐标;k为波数。计算群桩波浪力时需考虑群桩效应,即在单桩计算的基础上乘以群桩系数K,如表1所示。

表1 群桩系数KTab.1 Pile group coefficient K

对于大尺寸承台结构,当相邻承台间距与承台折算尺寸之比大于4时,可忽略相邻承台的影响。波浪作用于大尺寸承台的波浪力按式(9)计算。

(9)

式中,b为矩形柱体断面垂直于波向的宽度。

根据式(4)～式(9)即可计算单位长度小尺寸桩柱和大尺寸承台上的波浪力,并可通过简谐函数按分布力模式施加于车-轨-桥耦合系统。

1.3 地震附加动水压力

地震引起的附加动水压力可采用附加质量的方式考虑。文献[15]推导了圆柱体附加动水压力的精确解

(10)

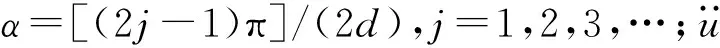
由此可知,精确的地震附加动水压力是结构变形的函数。当采用有限元法进行数值求解时,则式(10)可采用向量和矩阵表达为

(11)

其中

(12)

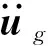
可利用刚性柱法对式(12)进行简化计算[16],同时文献[17]通过试验确定了矩形截面与圆形截面附加质量的换算系数。本文利用上述方法即可在车-轨-桥耦合系统中考虑地震附加动水压力。

2 计算参数

以某跨度(70+70+130+400+130+70+70)m的高速铁路跨海斜拉桥为例进行研究,总体布置如图2所示。主桥为双塔双索面半漂浮体系,主梁为混凝土桥面板与槽形钢箱梁的叠合梁;主塔采用混凝土桥塔,塔底设塔座、高6.0 m,塔柱采用箱形断面、横向设两道横系梁、高169.3 m;在连接墩(1#,8#)和辅助墩(2#,3#,6#,7#)处设竖向约束并在左侧设横向约束;索塔与主梁间设竖向约束和横向约束,纵向设带限位功能的黏滞阻尼器。斜拉索为镀锌平行钢丝索,二期恒载取131.2 kN/m。1#～8#桥墩的基础参数如表2所示。

表2 桥墩基础参数Tab.2 Parameters of pier foundation

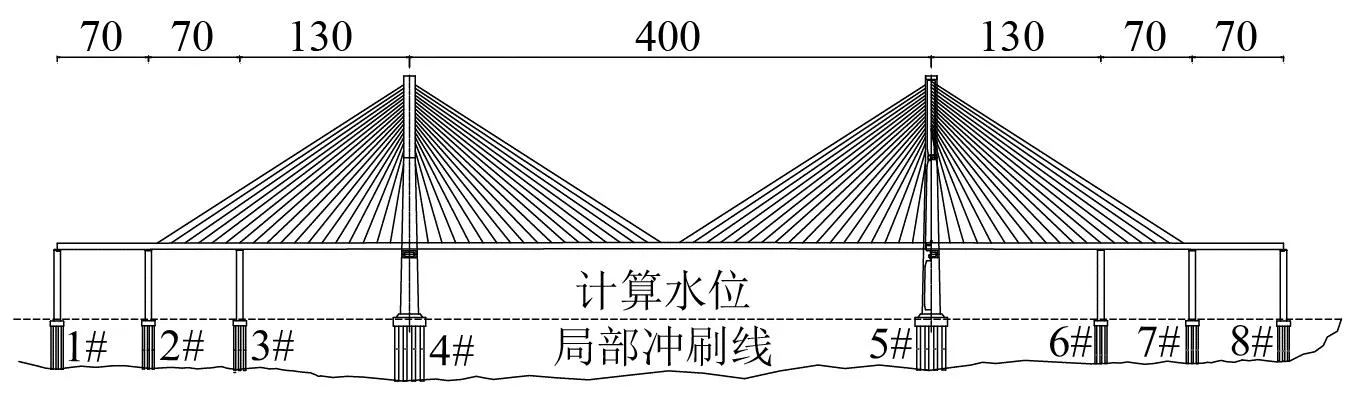
图2 结构布置图(m)Fig.2 Structural layout plan(m)

根据上述工程概况,利用有限元软件建立了全桥有限元模型,斜拉桥主梁、拉索、主塔等均采用空间梁单元模拟,利用主从约束模拟结构的边界条件。通过计算发现该桥的第1阶自振频率为0.145 Hz,与以往的计算结果一致[18]。模型中,局部冲刷线以上至计算水位可根据需要施加地震动水力附加质量,地震动水力附加质量的简化计算方法见1.3节,主塔处地震动水力附加质量的计算结果如表3所示。

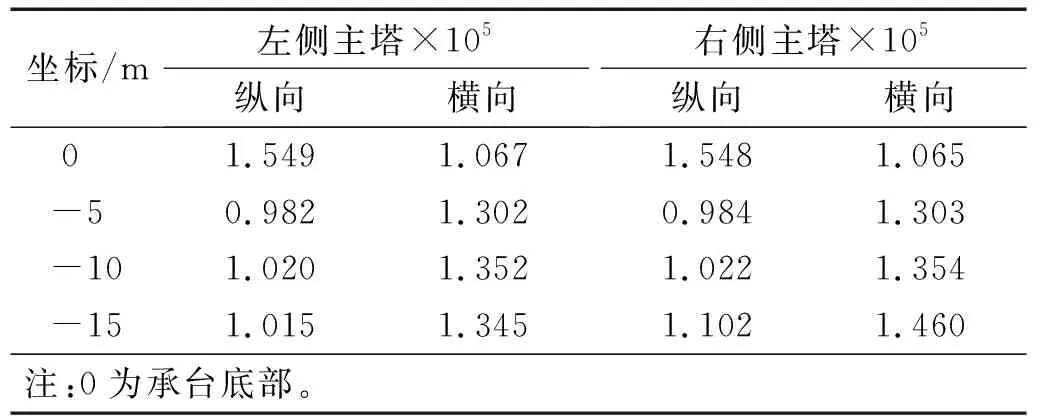
表3 地震动水力附加质量计算结果Tab.3 Calculation results of hydraulic additional mass of ground motion 单位:kg

根据该桥所在海域,参考JTS 145-2015《港口与航道水文规范》,选取崇武海洋站观测的波浪要素计算桥址处不同重现期下的波浪设计要素,重现期分别为10 a, 50 a和100 a,计算结果如表4所示。

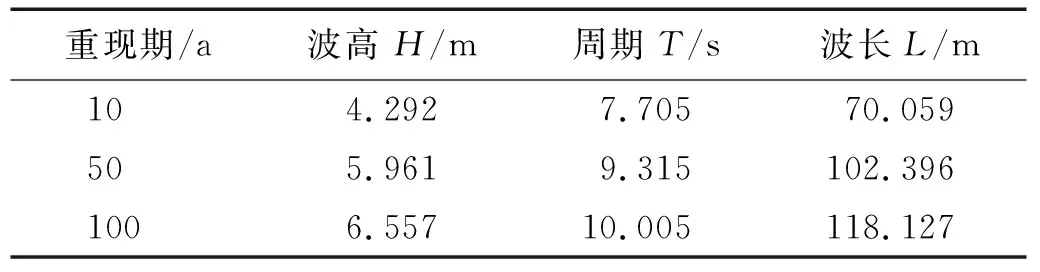
表4 不同重现期下的波浪要素Tab.4 Wave elements in different return periods

根据式(4)～式(9)和不同重现期下的波浪要素即可计算该斜拉桥受到的波浪力时程,桥塔墩柱桩基顶部节点和承台顶部节点不同重现期下的波浪力时程如图3所示。

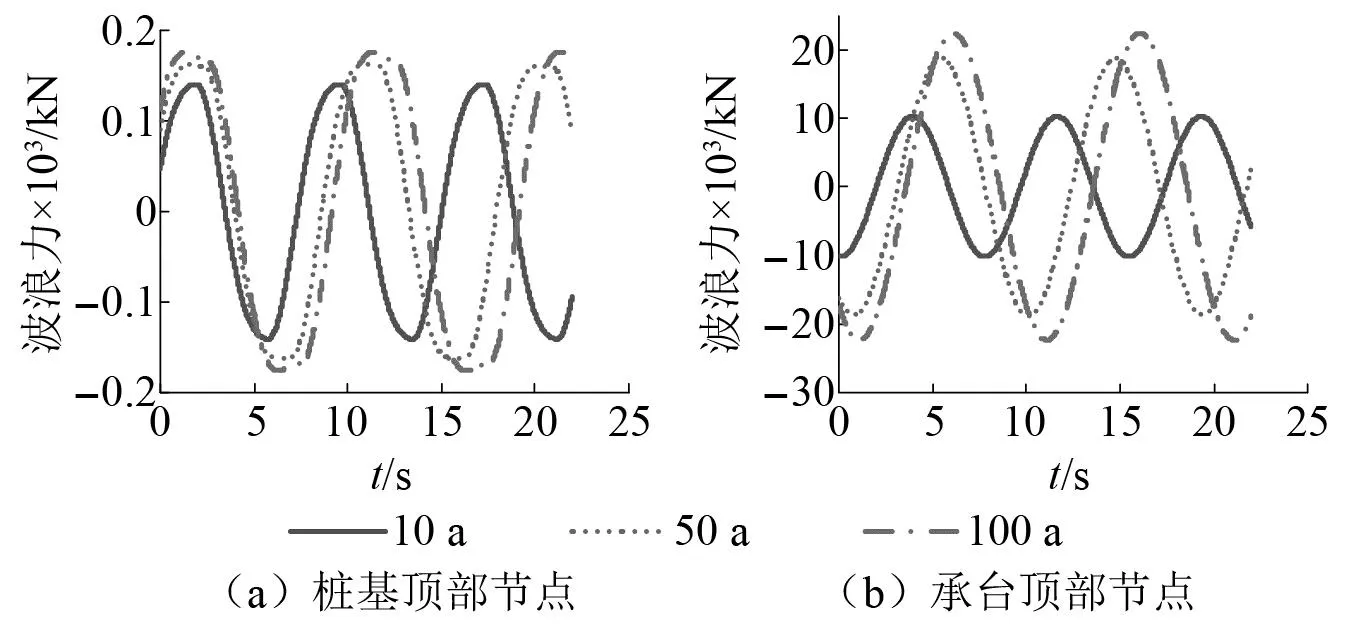
图3 波浪力时程Fig.3 Wave force time history

该桥位于地震8度区、Ⅱ类场地、特征周期分区为Ⅲ区,根据GB 50111-2006《铁路工程抗震设计规范》其地震动反应谱特征周期Tg为0.45 s。在太平洋地震工程研究中心选取了3条典型地震波作为输入,分别为El-Centro地震波(1979年、El-Centro Array #10台站、Tg=0.456 s)、Kobe地震波(1995年、Kakogawa台站、Tg=0.428 s)和Taft地震波(1952年、Taft Lincoln School台站、Tg=0.429 s),其加速度时程如图4所示。

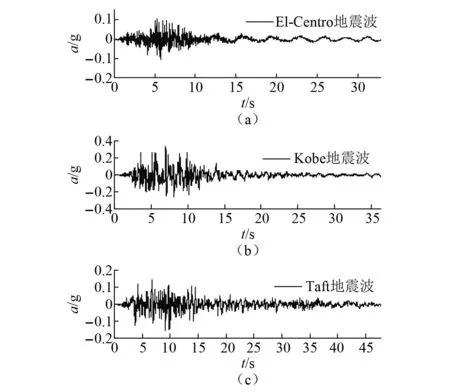
图4 地震波加速度时程Fig.4 Acceleration time history of seismic wave

列车模型采用国产高速列车,轨道模型采用板式无砟轨道,轨道不平顺通过德国低干扰谱模拟,参考文献[19],列车参数如表5所示。将上述车辆参数、轨道参数、桥梁参数以及波浪力时程、地震波加速度、地震动水力附加质量输入建立的分析模型和仿真分析程序,即可进行波浪-地震联合作用下车-轨-桥耦合振动仿真计算,时域积分步长取0.1 ms。

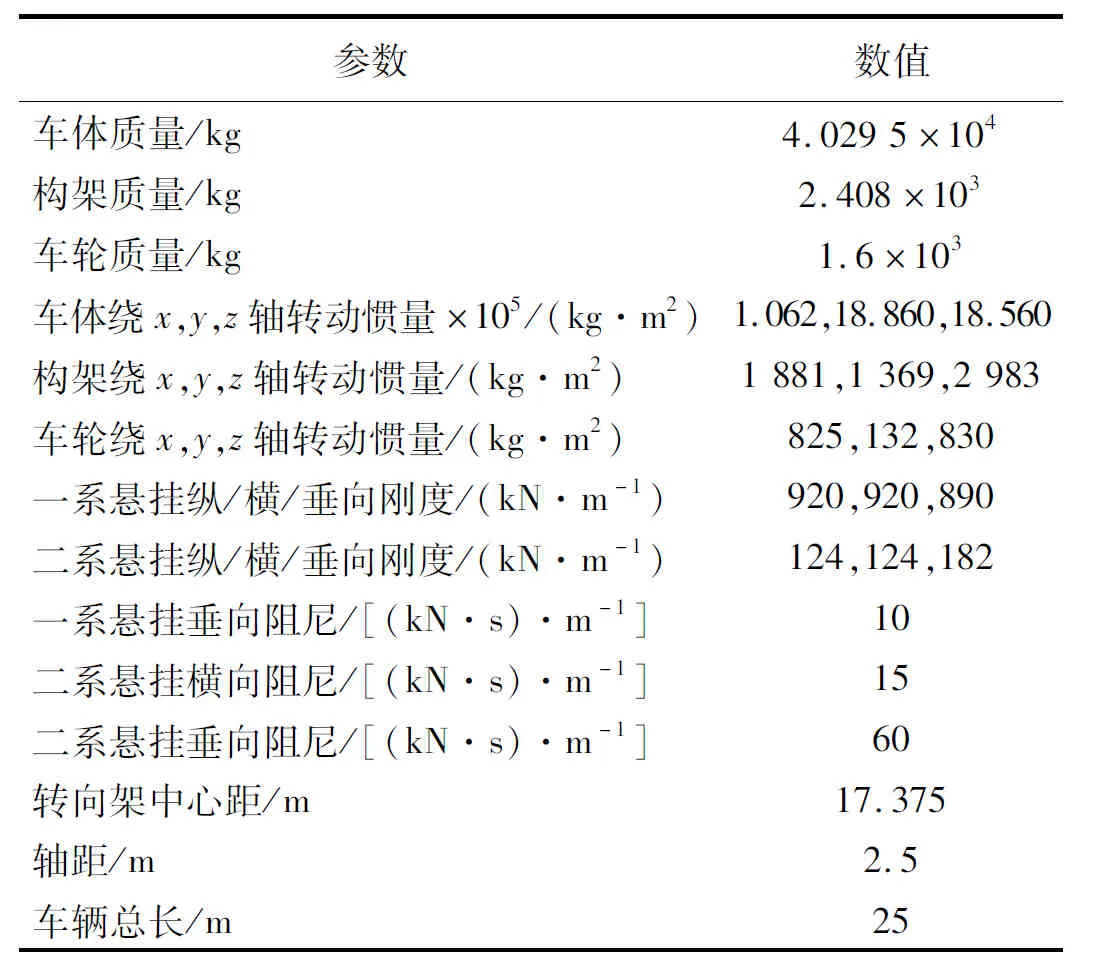
表5 车辆主要参数Tab.5 Main parameters of test train

3 算 例

3.1 影响因素分析

由于重现期10 a是跨海桥梁遭遇频次最高的波浪荷载,首先考察El-Centro地震、波浪荷载(重现期10 a)与列车荷载组合作用下高速铁路跨海斜拉桥-列车系统的耦合振动响应特征。计算时,将地震波按8度多遇地震进行规格化处理,沿横向和竖向同时输入,即横向地面峰值加速度调整为0.07g、竖向为0.046g;假设列车以时速300 km/h过桥;地震发生时刻与列车上桥时刻相同;波浪沿横桥向作用,作用时刻从0时刻开始,分析工况如表6所示。

表6 分析工况Tab.6 Analysis of working conditions

不同荷载工况下斜拉桥主梁跨中的位移时程、主梁跨中断面的钢轨位移时程、列车的横向和竖向加速度时程分别如图5～图7所示。同时对比了不同荷载工况下车桥耦合系统的桥梁位移响应幅值、钢轨位移响应幅值、车辆加速度响应幅值以及列车行车安全性指标幅值,如表7所示。

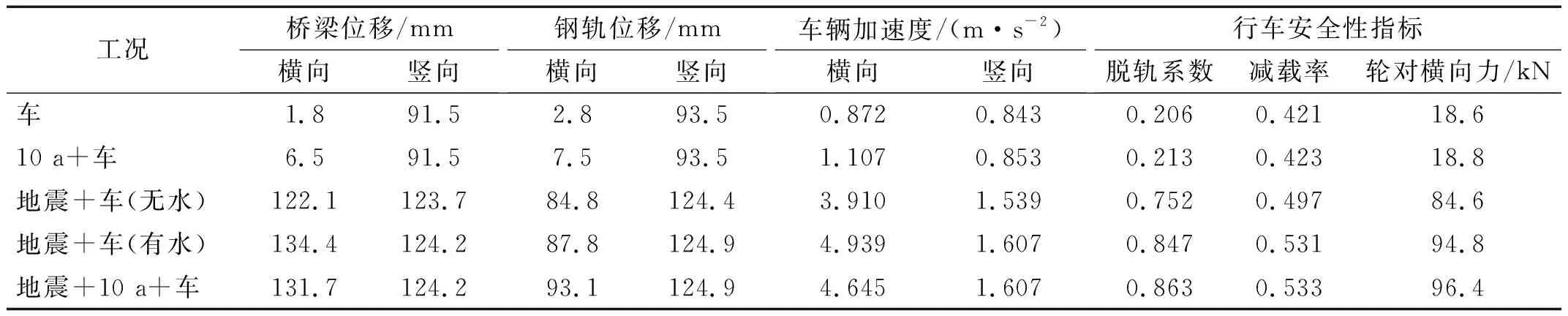
表7 不同工况下车桥系统动力响应幅值对比Tab.7 Comparison of dynamic response amplitudes of vehicle-bridge system under different working conditions

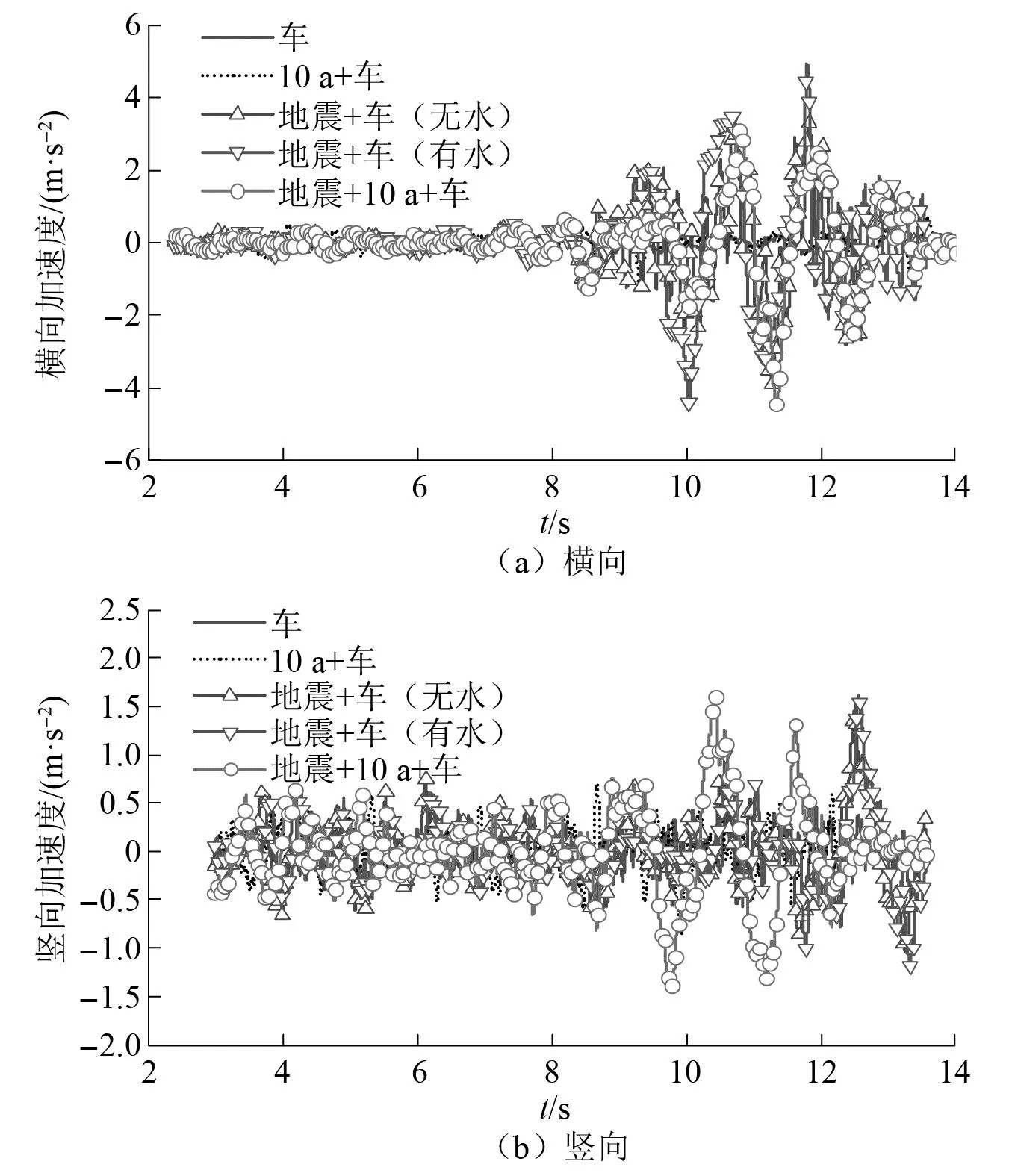
图7 车辆质心加速度时程Fig.7 Time history of vehicle centroid acceleration

由图5和表7可知:

(1) 对比工况1和工况2可知,波浪荷载对斜拉桥横向位移的贡献大于列车荷载,而对于桥梁的竖向位移,列车荷载起控制作用,波浪荷载几乎无影响。

(2) 对比工况3和工况4可知,考虑地震附加动水压力会显著增大斜拉桥主梁跨中的横向位移,增幅达10.1%。而地震附加动水压力对斜拉桥主梁跨中竖向位移的影响有限,相对差值仅为0.5%。由于车桥耦合振动中,桥梁的横向振动对列车系统的动力响应影响较大,因此在进行地震作用下跨海斜拉桥的车桥耦合振动分析时应考虑地震附加动水压力。

(3) 对比工况4和工况5,当同时考虑地震荷载和波浪荷载时,地震的影响远大于波浪,两种工况下主梁跨中的横向位移时程波形几乎重合,仅幅值有差异。同时,波浪-地震联合作用下(工况5)斜拉桥跨中的横向位移小于工况4,相对差值为-2.0%。分析原因,这是由于波浪荷载的作用周期远大于地震的振动周期,波浪荷载的峰值与地震荷载的峰值时刻不同、方向各异。由此可知,对于跨海桥梁车桥耦合振动分析应根据实际情况考虑波浪-地震联合作用。

由图6和表7可知,波浪荷载、地震附加动水压力对斜拉桥主梁跨中断面钢轨位移的影响与对斜拉桥主梁跨中位移的影响规律基本相似。具体表现为--波浪荷载对钢轨的横向位移有影响,而对钢轨的竖向位移几乎无影响,这是由于本文的波浪荷载只沿横桥向输入; 考虑地震附加动水压力后,钢轨的横向位移会显著增大,而竖向位移增幅有限; 波浪-地震联合荷载下钢轨的横向位移较工况4有小幅增大,但波形几乎完全一致,且峰值时刻完全相同。

由图7和表7可知:

(1) 波浪和地震均会显著增大桥上车辆质心的横向加速度,且地震比波浪的影响更大。例如,工况2相比工况1车辆质心的横向加速度增幅为26.9%,工况3相比工况2增幅达2.53倍。

(2) 对比工况3和工况4,当考虑地震附加动水压力时车辆质心的横向加速度较不考虑时增大了26.3%、竖向增大了4.4%。地震附加动水压力会显著增大桥上车辆的质心加速度。

(3) 对比工况4和工况5,波浪-地震联合作用下桥上车辆质心的横向加速度小于地震单独作用,这与波浪-地震联合作用对桥梁动力响应的影响规律一致,都是波浪荷载峰值与地震动峰值可能不一致产生的。

(4) 对于列车的行车安全性指标,考虑波浪荷载后行车安全性指标会略微增大(工况2),而当考虑地震后会显著增大(工况3),且考虑地震附加动水压力后会进一步增大(工况4),同时波浪-地震联合作用工况的列车行车安全性指标最大(工况5)。由此说明,波浪、地震均对跨海桥梁桥上列车的行车安全性有影响,且地震的影响大于波浪,高速铁路跨海斜拉桥需考虑波浪-地震的联合作用。

为进一步考察波浪-地震联合作用对跨海斜拉桥车桥系统动力响应的影响,分别将3条典型地震波与不同重现期的波浪荷载组合作用于耦合系统,计算车桥系统的动力响应,计算中根据前述结论均考虑地震附加动水压力。不同工况下桥梁跨中断面的横向动力响应幅值对比如表8所示。列车的各项行车安全性指标对比如表9所示。

表8 波浪-地震联合作用下主梁跨中横向动力响应幅值对比Tab.8 Transverse dynamic response amplitudes of mid-span section of main beam under combined wave-earthquake action

表9 波浪-地震联合作用下列车行车安全指标幅值对比Tab.9 Amplitude comparison of train safety index under combined wave-earthquake action

由表8可知,在波浪-地震联合作用下,当地震动强度保持不变时,随着波浪重现期的增大,桥梁的横向位移、横向加速度和钢轨横向位移均有增大的趋势。对于本文算例和计算条件,当重现期10 a,50 a和100 a相比不考虑波浪时,3条地震波作用下桥梁横向位移的平均增幅分别为0.3%,2.5%,4.9%,桥梁横向加速度的平均增幅为0.4%,1.0%,1.6%,钢轨横向位移的平均增幅为2.3%,3.9%,7.7%。

由表9可知:

(1) 考虑波浪-地震联合作用,不同地震波、波浪组合作用下桥上列车的行车安全性指标幅值存在明显差异。这是由于不同地震波包含的频率成分不同,只有靠近结构主要自振频率的分量才对结构的动力响应有贡献,而远离结构主要自振频率的分量则贡献较小。因此,在进行波浪-地震联合作用下的车桥耦合振动分析时需考虑多条地震波的计算结果进行综合评估。

(2) 同一波浪、不同地震波组合对桥上列车行车安全性指标的影响规律基本一致。当地震波强度保持不变,随着波浪重现期的增大,列车的行车安全性指标均增大。相比不考虑波浪作用,重现期10 a,50 a,100 a波浪作用下脱轨系数的平均增幅为3.6%,13.0%,13.8%;轮重减载率的平均增幅为3.4%,10.8%,12.5%;轮对横向力的平均增幅为5.0%,9.9%,10.6%。

综上所述,对于地震作用下高速铁路跨海斜拉桥的行车安全性研究,需考虑地震附加动水力的影响,同时应考虑波浪-地震的联合作用。

3.2 行车安全性分析

根据3.1节分析,针对该高速铁路跨海斜拉桥,以波浪重现期和列车车速为基本参数分析桥上列车的行车安全性。

波浪重现期分别取10 a(一般波浪)和100 a(极端波浪),同时与无波浪工况对比。列车车速分别取250～350 km/h,间距为25 km/h;取3条地震波与不同重现期波浪组合作用的平均值进行分析。根据TB 10002-2017《铁路桥涵设计规范》给出的指标评判列车过桥时的行车安全性,其指标如下

(13)

式中,P0为静轴重,根据本文车辆参数,轮对横向力限值指标为62.27 kN。不同重现期波浪-地震联合作用下指标1～指标3随车速的变化如图8所示。

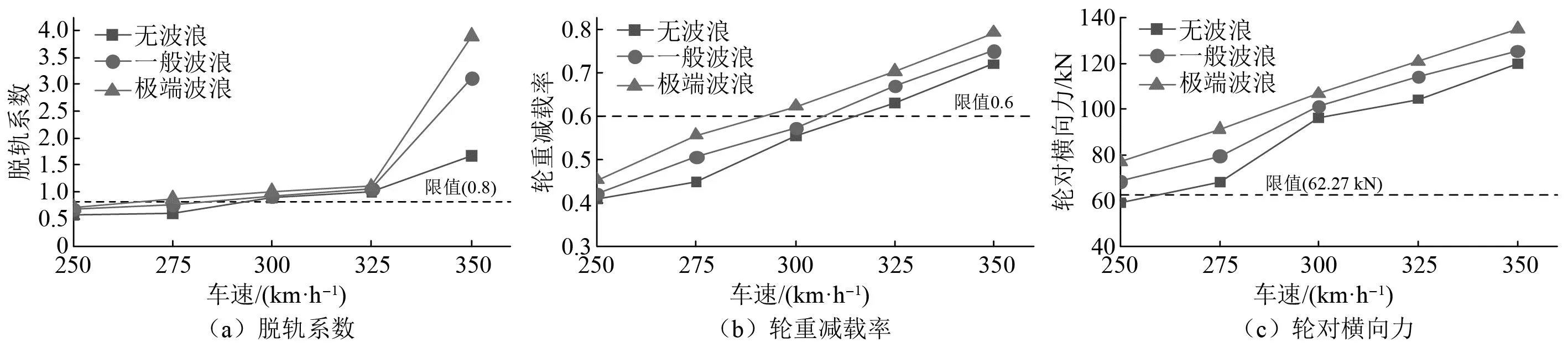
图8 列车行车安全性指标随车速的变化曲线Fig 8 Variation curve of train safety index with speed

由图8可知,在不同重现期波浪-地震联合作用下,列车的各项行车安全指标幅值均随车速的增大而增大,极端波浪大于一般波浪,且均大于无波浪工况。由此可见,对于高速铁路跨海斜拉桥的行车安全性研究,需考虑波浪-地震联合作用,且地震是影响桥上列车行车安全的主要因素,但当考虑波浪-地震联合作用后,其桥上列车的行车安全性会进一步降低。根据指标1～指标3,不同重现期波浪-地震联合作用下该高速铁路跨海斜拉桥桥上列车的安全车速阈值如表10所示。

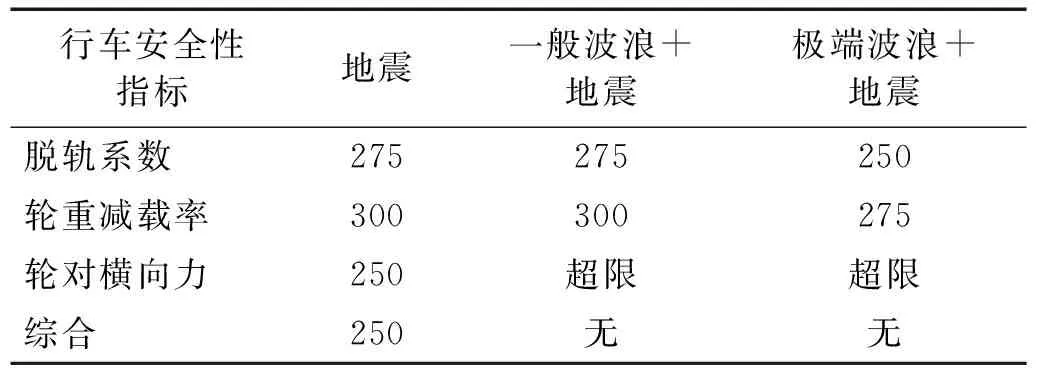
表10 列车的安全车速阈值Tab.10 Train safety speed threshold

由表10可知,根据不同的行车安全性指标得到的安全车速阈值有差异,因此需综合3项指标进行行车安全性评判。对于本文算例,地震单独作用下,该高速铁路跨海斜拉桥的安全车速阈值为250 km/h,而一般波浪-地震联合作用和极端波浪-地震联合作用下,由于桥上列车的轮对横向力均超限,计算范围内的所有车速均不安全,无安全车速阈值。由此可见,对于高速铁路跨海斜拉桥,波浪会严重威胁桥上列车的行车安全性,考虑波浪-地震的联合作用十分必要。

4 结 论

本文建立了波浪-地震联合作用下列车-轨道-桥梁耦合振动的分析方法,并以一座主跨400 m的高速铁路跨海斜拉桥为例,系统研究了波浪参数、地震动参数对车桥系统动力响应的影响,得到了以下几点结论:

(1) 对于高速铁路跨海斜拉桥,地震附加动水压力不可忽略。考虑地震附加动水压力会显著增大斜拉桥主梁跨中的横向动力响应及列车的行车安全性指标。对于本文算例,列车的3项行车安全性指标的增幅分别为12.6%,6.8%和12.1%。

(2) 对于高速铁路跨海斜拉桥,考虑波浪-地震的联合作用十分必要。随着波浪重现期的增大,桥梁的横向动力响应及列车的行车安全性指标均增大。对于本文算例,相比地震单独作用工况,100 a重现期波浪-地震联合作用工况下的3项列车行车安全性指标的平均增幅为13.8%,12.5%和10.6%。

(3) 对于高速铁路跨海斜拉桥,地震是影响桥上列车行车安全的主要因素,但当考虑波浪-地震联合作用后桥上列车的行车安全性会进一步降低。对于本文算例,综合3项列车行车安全性指标,单独地震作用下,该高速铁路跨海斜拉桥的安全车速阈值为250 km/h;而一般波浪-地震联合作用和极端波浪-地震联合作用下桥上列车的轮对横向力会超限,计算范围内无安全车速阈值。