基于动态合作博弈的天津市水资源优化配置研究

李春玲，孙亮科

(中水北方勘测设计研究有限责任公司，天津 300222)

水资源是生命存在的物质基础，是重要的战略资源，对社会经济发展关重要[1]。自古以来，人类部落的形成离不开水资源。现代城市的运转和发展更离不开水资源[2-3]。我国水资源匮乏，水资源总量仅为世界水资源总量的6%左右，人均水资源占有量低于世界人均水平。水资源存在地域分布不均衡、污染严重等问题，优化水资源配置，提高水资源使用效率尤为重要[4-5]。

在水资源优化配置过程中，政府作为社会经济活动的管理者，具有引导经济发展方向，促进经济可持续发展的作用，一般经济规律中，决定水资源配置方式的为市场[6]。由于水资源的稀缺性，水资源的优化过程中，利益相关者都想获取利益，引发矛盾。本文以政府与市场作为水资源优化配置参与主体，分析双方在此过程中的关系，基于博弈理论对水资源配置进行优化，以全新的视角和思路解决水资源优化配置问题。

1 政府与市场在水资源配置中的关系分析

水资源的优化配置过程中，应当由市场起决定性作用，更好的发挥政府的指导作用。我国是社会主义国家，水资源的配置除了遵循市场经济规律，还具有计划的成分，即市场和政府都要在水资源的优化配置过程中充分发挥各自的作用。因此，在我国的经济体制下，单纯的依靠政府干预或者市场经济规律是无法使水资源得到合理配置的。将政府干预与市场机制有机结合起来，兼顾公平和效率，才能够实现水资源最优配置。涉及公平的水资源开发与利用需要政府进行干预，涉及效率的供求和价格机制都需要市场进行决定。除民生用水，大多数与经济效益相关的水资源配置都需要市场机制得以实现。通过市场机制将水资源利用效率低的产业转移到水资源利用率高的产业，实现水资源的最优配置[7-8]。

水资源配置过程中，协调与互动是政府与市场最理想的关系。由于我国目前仍然处于社会主义初级阶段，各方面制度建设还不完善，当前发展背景下，政府应当准确定位，从“管理型”向“服务型”和“监督型”转变，建立健全各项体制机制。同时，水资源作为一种稀缺资源，为避免浪费，需要充分发挥“看不见的手”的作用，提高水资源利用效率，弥补行政管理模式的缺点，实现参与主体共赢[9]。

2 基于动态合作博弈的天津市水资源优化配置模型

水资源优化配置过程中，主要经历两个阶段：第一阶段是由政府完成的初始水权分配和费率核定，第二阶段是用水主体进行水权交易的过程。用水主体根据自身需求对取水量和用水量做出决定，政府的职责是保障生产生活的最基本用水和生态用水，并对初始水权分配进行调整。

政府无法在第二阶段对用水主体需求进行干预，只能在第一阶段对用水费率和初始水权分配进行决策。但是政府能够预测到在第二阶段用水主体势必会为了自身利益而采取行动，从而能够在第一阶段制定相应的对策进行宏观调控。

假设政府能够分配的总水量为Q，m3；公共水权为s，m3；水资源费率为t，%；初始水权为r，m3；(ri表示i地区分到的初始水权)，则可得：

(1)

假设X—实际需水量，m3；q1i—直接取水量，m3；q2i—新开发水源量，m3；q3i—节水量，m3。实际用水量大于总水量时，缺额部分由新开发水源或者提高水资源的利用效率来补足；当总水量大于初始水权量时，缺额部分则需要在市场中购买；总水量小于初始水权量时，则多余部分可在市场中出售。

在水资源交易市场中，需求关系同样也影响这水资源的价格，当供大于求时，价格下降，反之，则价格上升。采用古诺模型，水资源反需求函数为：

P(x)=a-bx(a，b>0)

(2)

(3)

其中，x—水资源供求差值，m3。

假设供水成本为C1i(q1i)(元)，新水源开发成本为C2i(q2i)(元)，节水成本为C3i(q3i)(元)，用水收益为Bi(q1i+q2i+q3i)，可以由此得出效益函数(元)：

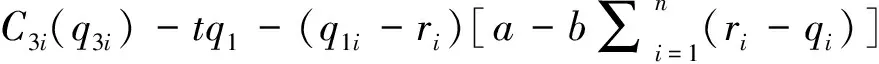
(4)

假设公共效益为d(s)，政府由管理水资源取得的水资源费和公共效益为F0，则：

(5)

由此，可得社会总效益为：

(6)

政府最大目标是社会效益和群众满意度，则目标函数可表示为：

Z=maxFT

(7)

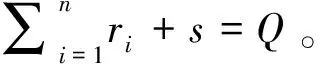
本文将水资源优化配置分为两个阶段，其博弈过程亦为两个阶段的动态博弈。在博弈过程中，子博弈要达到纳什均衡。根据逆向思维，要先对第二阶段进行求解，即在确定初始水权分配和水资源费率的前提下，求每个子博弈纳什均衡解。然后在求解第一阶段政府对初始水权的分配和水资源费率。

当边际效益为0时，效益最大，则有：

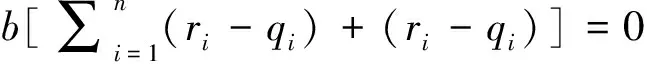
(8)

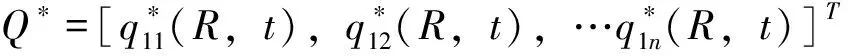
(9)

其中，q—最优取水量m3；R—获得的初始水权，m3。

求解第一阶段，将Q*带入社会总效益求解公式，得出：

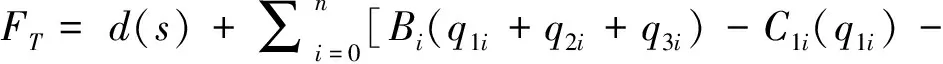
(10)

可解出社会总效益和初始水权，带入最大化社会总效益公式，求出最大化社会总效益。

上述两个阶段的博弈过程是双方在非合作状态下的博弈，但是在水资源的优化配置过程中，政府与市场是具有合作特点的博弈，即正和博弈。在合作博弈过程中，参与者的收益不会低于非合作状态下的收益。合作博弈状态下，整体收益提高，对合作后的收益问题进行分析，求出Shapley值。

在合作博弈过程中，一般用N={1，2，…n}表示博弈参与成员集合，其利益分配需要满足以下要求：

∑l∈nxi=v(N)

(11)

上式中，x—成员分得的收益，元；v(N)—集合成员的总收益元。并且，合作状态下的参与成员所得利益应不低于非合作状态下个人所获收益，即：

vi≤xi，i∈n

(12)

假设S={1，2，…m}是一个博弈联盟，满足：

∑l∈nxi≤v(S)，xi≥vi，i∈S

(13)

Shapley值是合作博弈的解，是根据计算贡献率来对收益进行分配的，其表达式为：

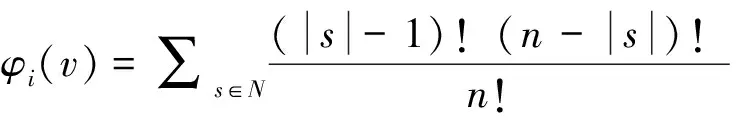
(14)

上式中，φi—成员i应得的利益，|s|—成员数，vS-v(S-{i})—成员i的贡献利益。水资源的优化配置过程中，假设双方是理性的，具有水资源量分别为r1和r2，合作目标可表示为：

(15)

其中，k1+k2=r1+r2。

同时，根据合作博弈的定义可得：

(16)

即合作总收益不低于非合作收益之和。

3 实证研究—天津市水资源优化配置分析

3.1 要素集与函数的界定

首先，对天津市水资源优化配置中的参与者集合进行确定，根据天津市行政区划，将参与者分为4部分区域，分别为市内六区、环城四区、滨海新区和远郊二区三县，具体见表1。

表1 参与者集合情况

同时，基于《天津市水资源公报》《天津市统计年鉴》《天津市水务发展统计》以及水务部门官网公布相关数据等资料和各类函数之间的关系，对天津市各区域的支付函数予以确定，其中包括用水收益函数、供水成本函数、新开发水源函数和节水费用函数，如题见表2。

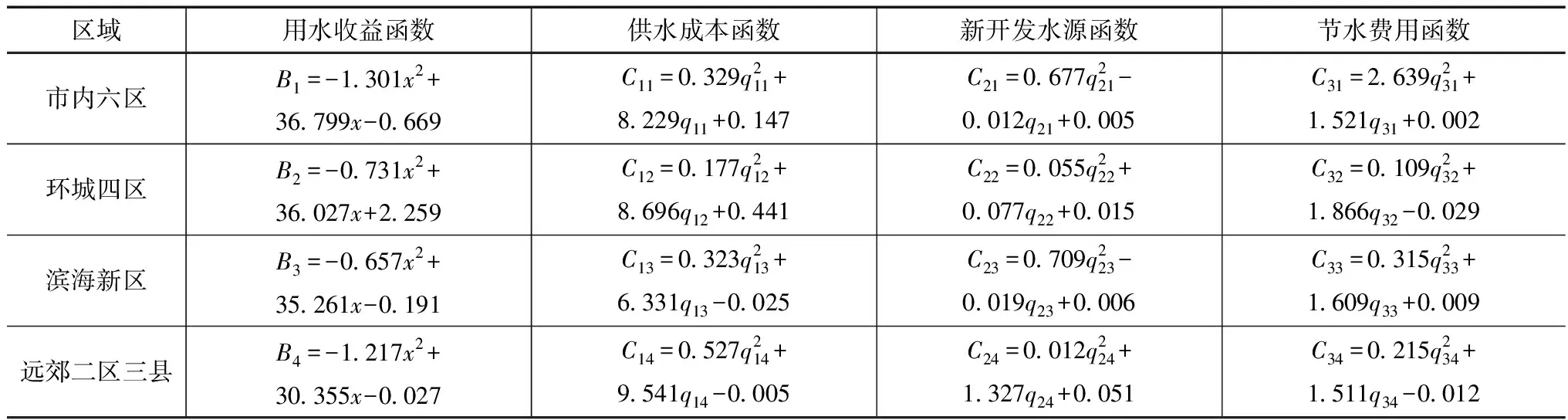
表2 天津市各区域支付函数 单位：亿元

3.2 初始水权的分配

将天津市近年来平均水资源量与入海量之间的差值作为可进行分配的总水权。初始水权进行合理分配时，应当遵循以下原则：

第一，优先保障基本用水需求，即在对水权进行分配时，要优先考虑各区域的居民生活用水和生态环境用水。

第二，遵循经济发展实际规律。天津市各区域经济发展具有不均衡性，导致水资源消耗情况也不近相同。因为，可以按照GDP来确定在生产用水方面的水权分配系数，其计算公式如下所示：

(17)

其中，αk—生活用水水权分配系数。

第三，适度照顾原则。天津市各区域发展不均衡，其工业生产、经济机构等也存在区别。在这种情况下，部分落后但耗水量高的工业难以在短时间内降低用水量。因此，初始水权进行分配时，应考虑对经济落后区域给予政策上的支持，引入政策权系数γ，该系数的取值可根据实际情况由多方协商予以确定，如在考虑政策权系数的情况下，k地区的初始水权分配系数计算公式如下：

(18)

天津市2021年各区域可分配初试水权及各区域人口、GDP情况见表3。

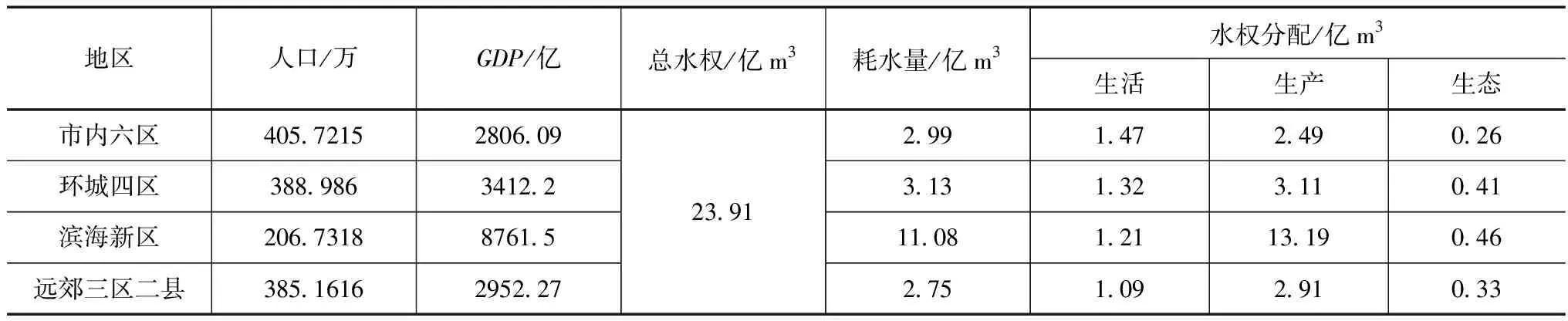
表3 天津市各区域初始水权分配情况

根据建立的合作博弈模型，设d(s)=0.49s，将其带入最大化社会总效益公式并进行计算，可以得出基于合作博弈理论的天津市各地区水资源优化配置结果，具体见表4。

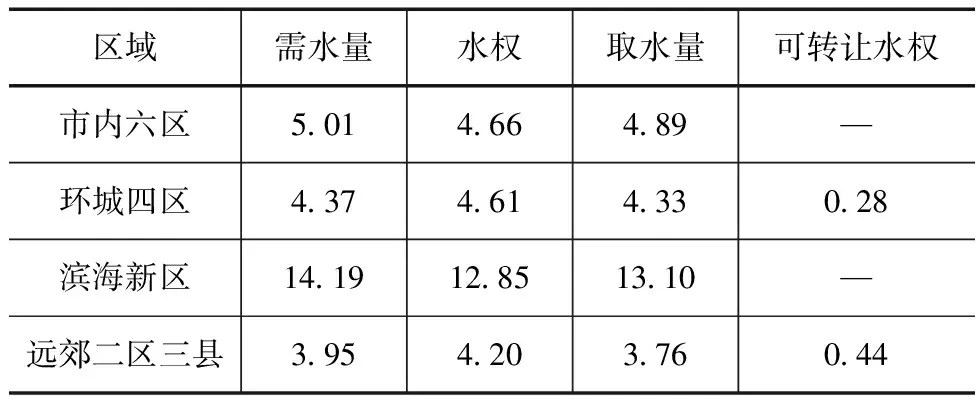
表4 天津市各地区水资源优化配置结果 单位：亿m3

如果采用节水措施或者进行技术创新以提高水资源利用效率将会大大提高有效水资源量，这就需要建立明确的利益分配机制，促使参与方由非合作状态向合作状态转变。

将不具有可转让水权的市内六区和滨海新区组成联盟S，根据贡献率计算公式，可得：

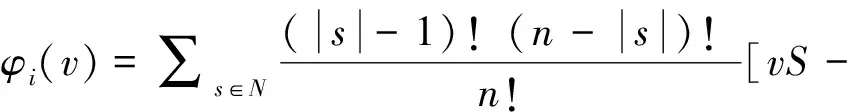
(19)

在天津市水资源优化配置的过程中可以看出，各参与主体之间存在着用水冲突，但在政府与市场的共同作用下，建立有效的取用水和水权交易机制，能够促进水资源的合理配置，促进水资源的可持续发展。

4 结论

充分考虑政府与市场在水资源配置中的作用，将动态合作博弈理论应用到水资源优化配置中，从新的视角出发建立了天津市水资源优化配置体系。结果表明，水资源配置既不能只依靠政府的调节作用，也不能全然根据市场经济规律进行水资源配置，需要双方合作，才能得到水资源优化配置的目的。基于动态博弈理论建立的政府与市场共同作用下的水资源优化配置模型能够优化水资源配置，为天津市在水资源优化配置方面的工作提供了全新的思路，符合我国社会经济可持续发展的宗旨。本文研究在考虑水权交易时，未考虑排污权及我国水权制度方面的问题，应重点关注该方面的问题。