改进Copula函数在中型水库枯期径流预测中的应用

白天竺

(辽宁省铁岭水文局，辽宁 铁岭 112000)

对于中型水库而言，其主要用于区域灌溉供水和发电，尤其是在枯水期，需要对其径流进行预测，从而制定相应的供水和发电计划[1]。因此对于中型水库而言，其枯水期径流预测精度的高低，直接影响水库的调度效益[2]。当前，对于水库枯水期径流预测取得一定研究成果[3-8]，其中Copula函数通过建立水库枯水期径流数据系列，对其未来变化概率进行趋势预测，预测效果要好于传统趋势预测模型，但传统Copula函数需要对不同数据系列进行概率密度的推求，使得其求解精度往往不高[9]。有学者针对传统Copula函数求解精度不高的局限，引入变量条件概率边际分布函数对其进行改进，并在国内一些大型水库枯水期径流预测中得到相关应用[10-15]，应用结果均好于传统Copula函数。但改进的Copula函数在中型水库枯水期径流预测中还未得到相关应用，大型水库多为季节调节型，其枯水期径流预测精度相比较高，而对于中型水库而言，其枯水期径流受季节调蓄作用影响较大，因此其径流预测难度较高，为提高中型水库枯水期径流预测的精度，引入改进的Copula函数对铁岭地区中型水库进行枯水期径流预测，研究成果对于中型水库枯水期径流预测方法具有重要参考价值。

1 改进的Copula函数

对于任何一个变量X和Y按照Copula函数原理建立联合概率法密度分布函数C(u，v)，其条件概率密度函数H(X，Y)的计算方程为：

H(X，Y)=C(u，v)

(1)

其中：

u=Fx(x)=P(X≤x)

(2)

v=FY(y)=P(Y≤y)

(3)

式中，u和v—变量条件概率密度函数；FX和FY—各变量对应的概率函数。

改进的Copula函数对水库枯水期径流采用二元模型进行概率密度分布函数的构建，并计算其联合概率分布函数的特征值：

(4)

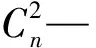
对构建的Copula函数采用K-S检验方法进行离差检验：

(5)

式中，Cemp、Ci—概率密度函数的边际密度计算系数。

相邻月份径流概率条件分布采用改进Copula函数进行描述，任一个系列的月枯期径流量采用前一月份已知的水库枯期径流进行推求，其计算步骤为：

(1)计算枯期径流序列边缘概率函数：

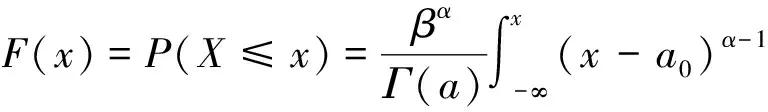
(6)

式中，α、β、α0—概率密度函数分布参数；x—径流预测值，m3；Γ(α)—条件概率密度分布函数。

(2)计算相邻月份枯期径流条件概率分布函数：

(7)

式中，ut，n+1—推求的相邻时间段的水库枯期径流量预测值，m3；St，St-1—不同时间段枯水期径流变量概率密度函数；xt，n+1—水库枯水期总的径流量预测值，m3；Ft—预测变量在时间t内的概率分布函数。

水库枯水期径流预测变量按照P-Ⅲ型分布进行计算：

(8)

式中，Φt—模型概率密度函数的偏态系数；xt，n+1，xt—不同时间段的径流预测样本数据系列。

改进的Copula函数对水库枯水期径流预测序列进行置信度区间的设置：

(9)

(10)

式中，uup和ulow—样本序列置信区间最高和最低值；xup和xlow—预测变量置信区间的最高和最低值。

2 模型应用

2.1 分析数据

以铁岭地区寇河诚信中型水库为具体实例，水库主要功能为灌溉供水，水库枯水期水量调度的关键在于其枯水期径流预测精度的高低。11月份～次年的4月份为诚信水库枯水期月份，结合水库2000—2020年近20年的枯水期径流数据系列作为分析数据，其中枯水期径流预测变量的概率密度分布函数采用2000—2015年径流数据序列进行计算，2011—2020年的枯水期径流系列主要用于对比分析改进前后的Copula函数在诚信水库枯水期径流预测的精度。

2.2 模型构建

采用诚信水库2000—2015年枯水期径流数据作为改进前后Copula函数变量计算序列样本，分别对不同时间尺度下模型的参数进行设定，结果见表1。

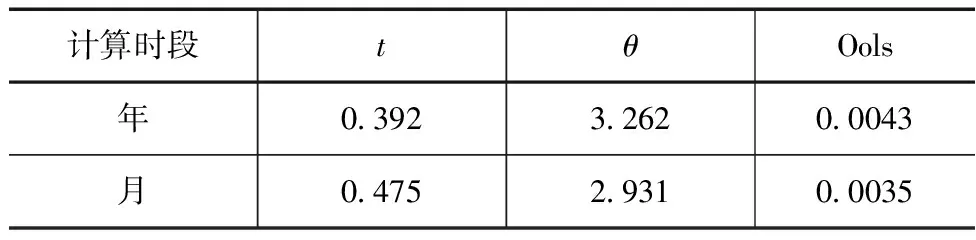
表1 改进前后Copula函数计算变量参数

2.3 年尺度预测精度对比

结合诚信水库在2011—2020年11月份～次年的4月份实际入库水量，对比分析改进前后的Copula函数在水库枯水期年尺度的入库水量的预测精度，并对改进前后模型预测值和实际入库量之间的相关系数和误差分布进行统计，统计分析结果见表2，如图1所示。

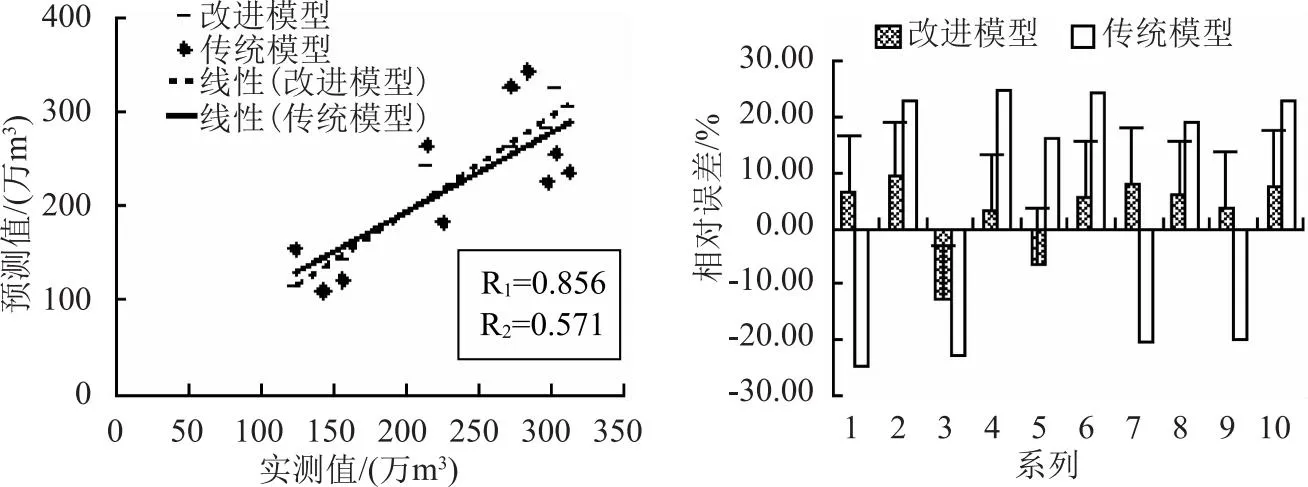
图1 诚信水库年尺度枯水期预测值和实际值误差统计

从改进前后Copula函数下诚信水库年尺度入库水量预测精度对比结果可看出，相比于改进前的Copula函数，改进后的Copula函数其枯水期径流预测精度得到明显改善，改进后诚信水库在枯水期年尺度下的入库水量预测值和实际入库水量之间的相对误差均在±10%以内，而改进前的相对误差均高于±10%，相比于改进前，改进后水库枯水期径流预测相对误差均值降低13.4%。从绝对误差对比可看出，改进前，各年份诚信水库枯水期径流预测值和实际入库量之间的绝对误差在27.72万m3～69.84万m3之间，且具有明显的年际变幅，而改进后诚信水库枯水期径流预测的绝对误差可控制在30万m3之内，且年际变幅较小。从改进前后Copula函数下诚信水库枯水期年尺度预测误差统计结果可看出，相比于改进前，改进后的相关系数达到0.856，相关系数提高0.285，相对误差分布也更为集中。

2.4 月尺度预测精度对比

对于水库而言，枯水期径流在月尺度变化更为明显，因此在年尺度精度对比分析基础上，分别结合改进的Copula函数对枯水期各月径流量进行预测精度对比，并统计改进前后径流预测的误差分布，统计结果分别见表3，如图2所示。

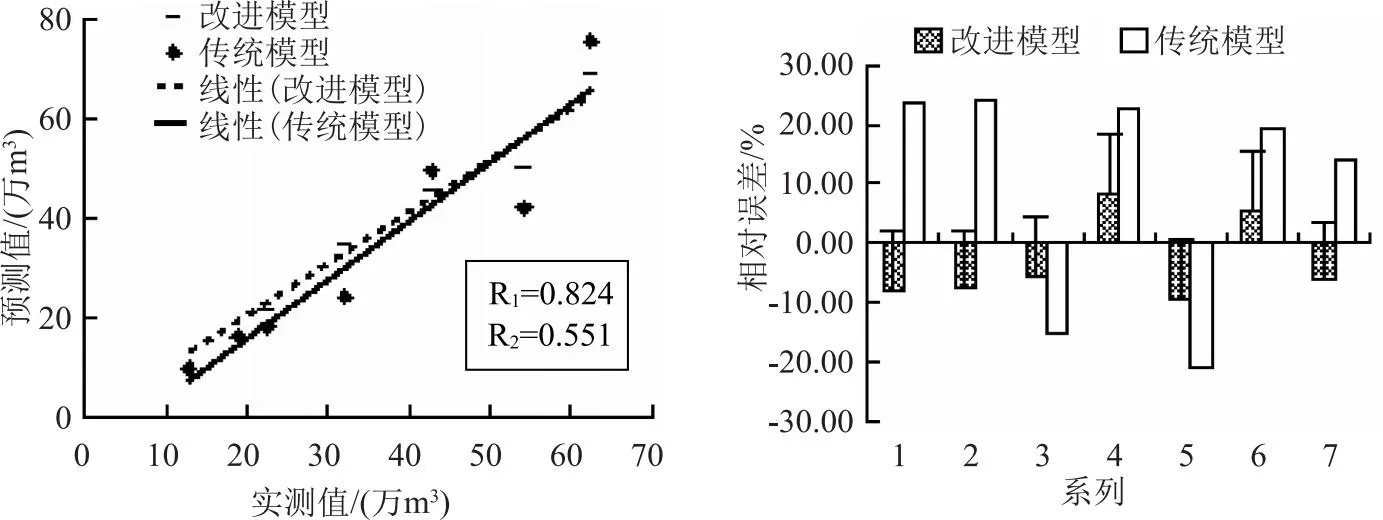
图2 诚信水库月尺度枯水期预测值和实际值误差统计

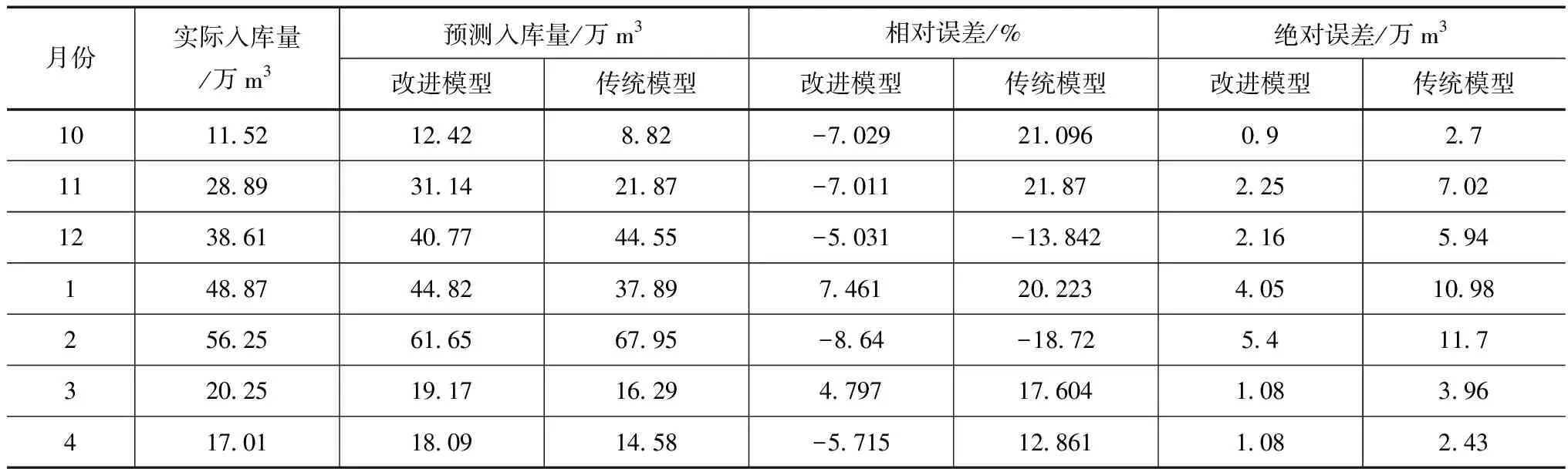
表3 改进前后Copula函数下诚信水库月尺度入库水量预测精度对比

从改进前后Copula函数下诚信水库月尺度入库水量预测精度对比可看出，相比于改进前，改进后的Copula函数下诚信水库月尺度入库水量预测精度也同样明显改善，改进后诚信水库枯水期各月入库水量预测值和实际入库水量之间的相对误差均在±10%以内，且要低于年尺度预测相对误差，这主要是因为年尺度下径流预测有均化现象，一定程度提高了其预测误差。相比于改进前，在月尺度上改进后的Copula函数下诚信水库月尺度入库水量预测值和实际入库水量之间的相对误差均值降低11.5%，绝对误差降低3.97万m3。从诚信水库月尺度枯水期预测值和实际值误差统计结果可看出，对于月尺度而言，改进后的Copula函数其径流预测值和实际入库水量之间的相关系数提高0.273，误差分布也相比于改进前更为集中。

3 结语

(1)在采用改进后Copula函数对中型水库进行枯水期径流预测时，应结合K-S检验对其预测变量序列的概率密度分布函数进行离差检验，检验系数低于0.95时其变量概率密度函数可通过检验。

(2)在进行中型水库枯水期逐月径流预测时，可降低其预测变量置信区间的上限值，通常可在0.5～1.5之间进行调整，可解决其不同月份之间径流预测差异较大的问题。

(3)降水量变化对于中型水库枯水期径流预测影响较大，在后续研究中可建立降水和径流量的双变量Copula函数，充分考虑降水变化对其枯水期径流影响。