基于代价敏感决策树的电压稳定在线评估方法

付兆隆,蒋轶周,梁鑫玉,王东哲

(1.三峡大学电气与新能源学院,湖北 宜昌 443002;2.上海电力大学电气工程学院,上海 200090;3.中咨工程管理咨询有限公司,北京 100048;4.东北电力大学电气工程学院,吉林 吉林 132012)

0 引言

众多大规模停电事故的发生往往是由某条线路或者某个节点的电压失稳引起的,并且很快扩散至整个线路,导致系统大面积瘫痪。因此,电压稳定是电力系统安全稳定运行的前提。

电力系统的众节点中,最容易失去稳定性的节点为薄弱节点,该节点能承受负载功率的范围最小,即该节点的稳定程度就在一定程度上代替了整个电力系统的稳定程度。文献[1]说明了电力系统中有1条线路或1个节点的电压临近崩溃,那么此电力系统就是不稳定的。通常采用灵敏度指标来判断薄弱节点、薄弱区域,常见的灵敏度指标有网损灵敏度指标和电压灵敏度指标[2-6]。但是这些单一的灵敏度指标对于识别薄弱节点或识别薄弱区域的准确性不高,很难应用到实际工程。聚类算法可以将数据按特征进行分类,属于无监督算法,在电力系统中应用广泛,包括电力系统负荷预测、变压器故障分类等。相比于传统的聚类算法,模糊聚类分析方法引入了隶属度的概念,分析隶属于各类别的程度,而不是非此即彼的判断,更符合实际情况。文献[7-9]将模糊聚类应用于变压器的故障分类中。文献[10]将模糊聚类应用于电能质量综合评估中。因此,可将聚类算法与电压灵敏度指标相结合来准确识别出电压薄弱节点区域。

传统的电压稳定分析方法不仅计算量很大,而且无法实时检测到实际的电压稳定运行状态[11-12]。随着PMU[13]问世,其在电力领域应用广泛,该技术可以实时提供电力系统大量精确、可靠、高速的同步数据,为电力系统在线分析提供可能。

综上,本文将模糊聚类与灵敏度指标相结合对电压薄弱点进行分区,相比起单一的灵敏度指标电压薄弱点分区更加准确。然后,采用基于代价敏感决策树模型对电压稳定在线评估,相比于传统决策树,电压稳定/失稳的判别更加准确。

1 灵敏度指标

1.1 网损灵敏度指标

网损灵敏度为

(1)

式中:Q、U和θ分别为注入节点的无功、节电电压和相角。

经过变化可得网损灵敏度:

(2)

由式(2)可知,网损灵敏度也与潮流雅可比矩阵有关。当电压崩溃时雅可比矩阵行列式的数值可以无限接近于零,此时网损灵敏度的数值就可以无限扩大,由此检验了网损灵敏度的有效性、合理性。在实际中,当网损灵敏度值达到相应的阈值后,便可以判断整个网络电压处于崩溃阶段。

计算各个节点网损灵敏度只要求在每次潮流运算的基础上,再增加少量运算。所以,网损灵敏度指标具有运算简便、统计效率高、精确度高的优势。具体计算流程如图1所示。

图1 网损灵敏度法流程

1.2 电压/无功灵敏度指标

用静态模型来表述电压和无功的灵活性指标,通过计算简化雅可比矩阵数目中最小的特征值和最大特征向量,这些特征值与电压/无功变化相关,提供了电压不稳定的相对量度,可以从电压与无功的关系来分析电压的稳定性[14-15]。计算方法如下。

线性化静态系统功率-电压方程为

(3)

式中:ΔP、ΔQ、Δθ、ΔV分别为节点电压的有功微增量、无功微增量、相角微增量、电压微增量;JPθ、JPV、JQθ、JQV分别为潮流偏微分方程形成的雅可比矩阵的子矩阵。

令ΔP=0,则

(4)

具体求解简化雅可比矩阵特征值和特征向量见文献[16]。

得到节点k的电压-无功灵敏度为

(5)

式中:Mki为第k个节点简化雅可比矩阵的第i列右特征向量;Nik为第k个节点简化雅可比矩阵的第i列左特征向量;λi为第i个特征值。

2 基于改进模糊C聚类算法的电压薄弱区域识别

2.1 模糊聚类的原理及应用

聚类算法的基本原理是把所有数据样本都按提前设置的条件以及其本身的规律加以区别和划分,在这一步骤中,由于没有任何经验,也没有他人干预,只靠数据本身的相似性成为区分类型的标准,从而构成了无监督计算。常用的聚类算法有K-means聚类算法、层次分析法等,聚类算法能够从样本的数据特征中发掘出信息和规则,是一种信息处理很有效的方法。因其计算效率高、计算准确、求解方便等优点在许多领域发挥着重要作用,例如数据挖掘、计算机视觉、图像分割等。

模糊聚类和传统的聚类算法不同,其抛弃了传统算法非“0”即“1”的思想,不再有明显界限。模糊聚类算法是在传统聚类算法的基础上对模糊性问题进行分析,特点是数据不是纯粹属于或者纯粹不属于某个分类,描述的是数据在一定程度上属于某个分类,这一思想相比于传统的聚类分析算法更加合理、高效。

2.2 模糊C聚类算法

模糊C聚类算法是一种非监督模式的识别方法,能够定量表征样本对类别的从属程度[14]。利用模糊数学思想求出隶属于各类别的程度,在工程实际问题中得到了广泛的应用。

假设数据样本有n个样本,X={x1,x2,…,xn},每个样本都具有m个特征,这样就可以得到一个n×m阶的原始数据矩阵。聚类中心为v={v1,v2,…,vc};隶属度矩阵为U={uij},其中uij为样本数据j对i类的隶属度,uij∈[0,1]。则模糊C聚类算法的目标函数为

(6)

(7)

(8)

(9)

式中:m为模糊加权系数,一般取m=2。

通过构造拉格朗日函数得到迭代公式:

(10)

(11)

式中:k为迭代次数,当目标函数达到收敛条件是聚类结束。

2.3 模糊C聚类算法的缺点及改进方法

模糊C聚类算法存在如下2个缺点。

a. 在传统模糊C聚类算法中,初始聚类中心和聚类数都是通过随机初始化或人为设定的,聚类结果的好坏依赖于初始值的选取。初值选择不合理,则会导致聚类结果和实际相差较大。

b. 传统模糊C聚类算法仅对聚类中心附近的数据具有较好的分类效果,有效的刻画区间比较小,容易陷入局部极值的问题。

为了解决上述2个问题,本文首先利用聚类有效性指标[17]来确定最佳聚类中心数,其次对隶属度迭代函数进行重构。

(12)

由式(12)可知,S越小,聚类结果越好,效果最佳。

对于解决问题2中传统模糊C聚类易陷入局部最优解的问题,本文对模糊C聚类的隶属函数进行重构,首先采用基于负指数函数的相似度指标:

ηij=e-adij

(13)

式中:a为灵敏系数,用于调整相似度函数的灵敏程度;dij为两点之间的欧氏距离;ηij为两点的相似程度。

然后,对某样本对所有聚类中心的相似指标进行标准化,构建出隶属度函数:

(14)

通过重构后的迭代函数可知两点之间的相似度控制在0～1,较原有模型变得较为平缓,度量的有效范围变宽,在一定程度上避免了聚类结果陷入局部最优解的可能性。样本对聚类中心的隶属度随着对聚类中心的远离单调递减。

2.4 基于改进模糊C聚类算法的薄弱区域识别流程

图2 薄弱节点分区流程

具体流程如下。

步骤1:收集节点数据,计算各个节点的灵敏度矩阵,并对其数量级数据进行归一化处理,使这些数据分布在[0,1]区间;

步骤2:初始化模糊C聚类算法的参数;

步骤3:由式(13)、式(14)得到新的隶属度矩阵U(k);

步骤4:令v=v+1,若满足收敛阈值ε,则得到聚类数为v的聚类结果;否则回到步骤2;

步骤6:得到多个聚类中心数的聚类有效性指标,确定最佳的聚类中心数;

步骤7:输出电压薄弱点的分区结果。

通过此方法对正常网架和N-1事故进行电压薄弱分区识别,得到了大量电压稳定/失稳的数据,为在线电压稳定评估提供了原始的数据样本。

3 基于代价敏感决策树的电压稳定在线评估

3.1 引入代价敏感机制的决策树算法

常见的分类法包括决策树、支持向量机、神经网络[18-19]等。决策树相较于其他分类方法,有着计算简单、计算速度快、输出结果易于理解等优点,适用于实现在线电压稳定分析。决策树C4.5算法的具体计算流程见文献[20]。

由于在电力系统运行中一般有一定的安全裕度,因此样本中的电压稳定样本占大多数,电压失稳的样本很少,两者样本数量会失衡。如果在电压稳定评估过程中,电压稳定样本被误判为电压失稳,则增加了工作人员的工作量;电压失稳样本被判定为电压稳定,则后果严重。由此可知,电压失稳被判为电压稳定的后果十分严重。

本文将代价敏感机制[21]引入电压稳定决策树分类中,改变样本权重,而无需改变样本的分布,从而达到电压稳定预测更加准确。

在决策树的基础上设定代价矩阵如表1所示。

表1 代价矩阵

由表1可知,cost-+、cost+-分别为误判的代价;cost--、cost++为预测正确,令其为0。由于电压失稳误判为电压稳定的后果更加严重,需要调整这两者之间代价,加强对失稳样本的学习。根据表1对样本权重进行调整,初始样本权重值为

(15)

(16)

式中:w-、w+分别为电压失稳和电压稳定的初始权值;N-、N+分别为电压失稳和电压稳定的样本数。

通过权重系数w,将决策树C4.5中的样本比例调整为加权比例p:

(17)

(18)

式中:pw-、pw+分别为电压失稳和电压稳定的加权比例。

通过加权比例,提高电压失稳样本的权重,减少漏判电压失稳样本的风险。

3.2 电压稳定在线评估流程

决策树在线监测依靠PMU数据的实时采集,从而实现电压稳定在线评估。具体流程见图3。

图3 电压稳定在线评估流程

a. 预测第2天的负荷水平、发电机开机状态、网架结构等。

b. 判断是否为新的运行方式。如果是新的运行方式,则生成新的决策树;如果不是,则利用决策规则在线判断。

c. 输出电压稳定或失稳结果。

4 算例分析

在如图4所示的IEEE39节点系统上进行仿真,验证本文采用的电压薄弱区域识别方法的准确性。并通过文献[20]中某地区电压失稳、稳定样本分析本文采用的电压稳定在线评估方法的有效性。

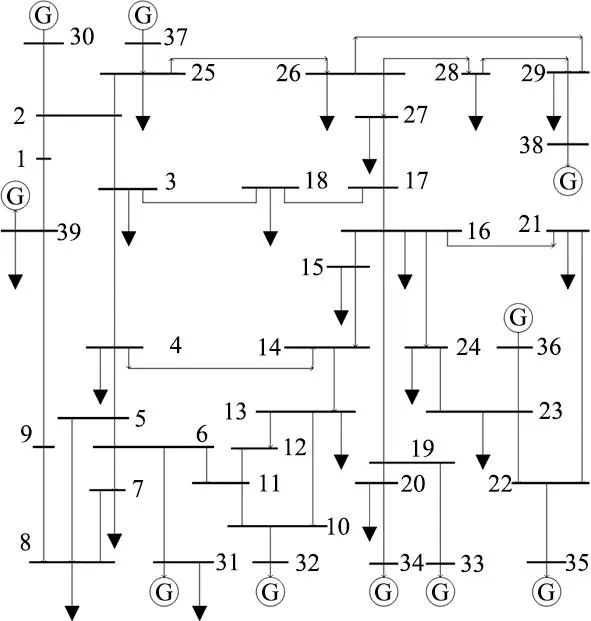
图4 IEEE39节点系统

4.1 验证电压薄弱分区识别方法准确性

本文采用聚类有效性指标来确定聚类中心数,经过计算可得,当聚类数为3时,聚类有效性指标S最小,即聚类效果最佳。按严重程度分为薄弱区域、次薄弱区域和不薄弱区域3类。聚类分区结果如表2所示。

表2 聚类分区结果

将3种灵敏度指标的薄弱点分区结果与本文采用聚类分析结果对比,以模态分析为标准,网损/有功灵敏度指标对薄弱点分区结果见表3。

表3 网损/有功灵敏度指标分区结果

网损/无功灵敏度指标对薄弱点分区结果见表4。

电压/无功灵敏度指标对薄弱点分区结果见表5。

表5 电压/无功灵敏度指标分区结果

模态分析指标对薄弱点分区结果见表6。

由表2—表6对比分析可得,聚类算法得到的电压薄弱节点区域、次薄弱节点区域和由模态分析得到的电压薄弱点分区、次电压薄弱节点分析非常接近,尤其是在薄弱区域的判断上,两者一致。另外3种灵敏性指标对电压薄弱点分区的结果与模态分析[22]的结果相差较大,无法准确判断出薄弱区域。由此可见,通过模糊聚类算法得到的电压薄弱点分区的结果较为准确,且计算效率高、计算简单,同时也避免了单一灵敏度指标分析结果相差较大的风险。

4.2 验证电压稳定在线评估方法的有效性

采用某地区实际电压稳定/失稳样本进行分析电压稳定在线评估的有效性。该样本包括4605个稳定样本和314个失稳样本。

采用混淆矩阵、精度、召回率和调和平均数[23-26]为模型的评价指标用于分析采用的基于代价敏感决策树相比于传统决策树更加准确、有效。验证结果见表7。

表7 传统决策树与本文采用方法比较

传统的决策树在分类中对待每个样本都是平等的,因此其漏警率为1.68%。而引入代价敏感的决策树其对漏警进行3倍惩罚,其结果漏警率为0,有效预防了电压失稳被判别为电压稳定的事故。综合考虑这些指标,验证了引入代价敏感决策树判断电压稳定/失稳的有效性。

5 结语

电压薄弱点分区判定是电压安全评估的重要组成部分。本文针对模糊C聚类算法的2点不足,采用聚类有效性指标和重构隶属度函数对其进行改进。然后,将灵敏度指标和模糊聚类相结合对电压薄弱点进行分区,并对电网正常运行和N-1事故进行仿真分析,得到大量数据,形成判断电压稳定/失稳的样本数据。最后,基于代价敏感决策树模型对电压稳定在线评估。在IEEE39节点系统上验证本文采用的电压薄弱点分区方法相比于单一指标的准确性,并对某一地区电压稳定/失稳样本数据进行仿真分析,验证本文采用的电压稳定在线评估方法的有效性。