新能源接入电网振荡中心快速识别方法

章玉杰,刘 绪,庞家彧,单 哲,刘艳梅

(1.国网江苏省电力有限公司超高压分公司,江苏 南京 211100;2.国网辽宁省电力有限公司物资分公司,辽宁 沈阳 110006)

0 引言

“双碳”目标下,构建以风电、光伏、水电等新能源为主体电源的新型电力系统成为主流趋势[1]。随着新能源接入电网的比例日益提高,其间歇性、波动性、随机性等特点对电网的安全稳定运行带来较大的影响,尤其当发生新能源大面积脱网和外送通道发生三相短路等严重故障时,电网振荡和暂态稳定性问题突出[2-4]。此外,新能源通过电力电子装置大规模并网,导致接入近区送端电网动态行为愈趋复杂,稳定特性发生了巨大变化,保障电网安全的稳定控制技术在以电力电子型设备为主要设备的新型电力系统中面临新的需求和挑战。

近年来,随着相量测量单元(PMS)在电力系统的广泛应用,挖掘广域量测系统(WAMS)实时、全局电力大数据中反映系统稳定特征的关键数据进行暂态稳定分析与控制、距离保护振荡闭锁以及失步解列等技术成为研究热点[5-8]。文献[8]通过研究系统振荡中心联络断面电压与系统暂态失稳功角的映射关系,提出了一种基于振荡中心联络断面受扰电压轨迹时域积分的暂态失稳判别方法。

基于理论研究成果,学术界和工业界对基于电网广域测量大数据的安全稳定控制技术在高比例新能源接入电网中的实际应用进行了探索[9-12]。工程应用结果表明,基于广域响应的稳定控制技术能够快速、有效地对系统稳定性进行评估;但同时也存在一定的不足,如依赖于能够敏感反映系统稳定特征的振荡中心观测点的选取,目前大多采用启发式人工选点方式。因此,研究如何在电网受扰后快速辨识系统重要断面振荡中心、确定重点观测站点,对于电网稳定控制具有重要意义。

关于电力系统振荡中心的研究,文献[13]较早地揭示了其变化原因并研究了系统发生失步振荡时电压公式及其变化特征,提出了基于Ucosφ的失步解列装置启动判据。文献[14]针对基于本地量的失步解列装置进行了研究,提出了利用阻抗角的变化时序及功率变化过零点判断振荡中心是否在线路上的方法。文献[15]指出传统失步解列装置存在的问题,并提出了自适应解列的必要性。振荡中心在上述暂态失稳判别和失步解列研究中具有重要地位,其运行特征和原理也有较多的研究。文献[16]提出了一种利用线路两侧电气量频率的差异识别系统振荡中心的方法。文献[17]研究了机电暂态仿真过程中振荡中心的计算方法、振荡中心的特点和变化规律。文献[18]研究了线路阻抗不均导致振荡中心偏移的规律。

本文在前期理论研究和工程应用基础上,进一步充分利用广域测量大数据的全局性和实时性的特点,深入研究了电力系统发生扰动后,系统振荡中心的变化过程与机理,提出一种基于广域量测大数据的电力系统振荡中心快速识别方法。该方法无需考虑系统和线路阻抗,仅需少量观测点电压量测相量数据即可快速筛选并确定受扰后系统重要断面(线路)振荡中心位置。通过IEEE39节点系统算例和中国南方电网实际电网算例验证了本文方法的有效性,可为新能源接入电网受扰后系统振荡薄弱断面快速识别提供参考。

1 振荡中心的定义

在电力系统振荡过程中,通常可等效为两机群振荡模式,可近似采用如图1所示的两机等值系统来描述其电气特性[13]。

图1 等值两机系统

图1中,EM和EN分别为两侧等值机群电势,C点为系统振荡中心。两机等值系统电压相量图如图2所示。

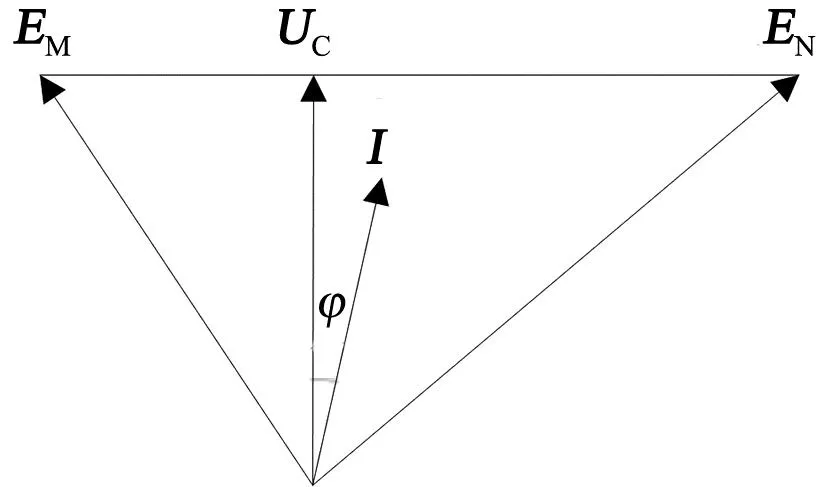
图2 等值两机系统电压相量图

两机系统发生振荡时,在两侧电势角度差逐渐变大的过程中,两系统中间各点电压会发生变化,最低点电压逐渐降低,这个电压最低点就是振荡中心。因此,振荡中心定义为电力系统振荡过程中同调机群之间电压幅值最小的点,通常位于2个区域和地区之间的联络线上。

2 线路振荡中心识别方法

振荡中心是电压幅值最小的点,如果线路存在振荡中心,则该点的电压低于线路两端母线电压。图3中电压最低点落在线路外侧,即线路中不存在振荡中心,图4中电压最低点落在线路中间,即线路中存在振荡中心。

图3 不存在最低电压的线路电压相量图

图4 存在最低电压的线路电压相量图

如图4所示,设线路两侧电压相量为U1和U2,相角差为θ0,U1与U1-U2相角差为θ1,U2与U2-U1相角差为θ2。假定线路上各点电压沿着U1和U2之间的连线均匀分布,则振荡中心电压为与该连线垂直的电压,即图4中的U0。

根据余弦定理得:

(1)

(2)

(3)

记|U1|=k|U2|,则有:

|U1-U2|2=(k2+1)|U2|2-2k|U2|2cosθ0

(4)

由相量图可知,θ1和θ2均为锐角,于是有:

(5)

联立式(4)和式(5),可得线路存在振荡中心的充要条件判据为

(6)

记振荡中心距离线路一侧距离与线路长度之比为ρ,则:

(7)

振荡中心电压幅值为

(8)

3 基于广域信息的振荡中心识别

通过分析推导可知,系统振荡中心存在于1条或几条关键线路上。可通过广域量测系统实时获取系统线路两侧的电压幅值和相角信息对系统振荡中心进行实时识别和跟踪,实现步骤如下。

a. 选择观测线路,对指定线路进行实时监测,并获取其两侧母线电压幅值和相角信息;

b. 利用式(6)判据对观测线路进行振荡中心识别,记录线路振荡次数和振荡中心位置;

c. 根据线路振荡中心电压和振荡次数筛选主振荡线路,确定系统的振荡中心。

具体算法实现流程如图5所示。

图5 振荡中心识别流程

4 算例分析

4.1 IEEE39节点系统算例

IEEE39节点系统结构如图6所示,采用PSD-BPA软件时域仿真结果模拟实时广域量测数据,仿真步长为0.02 s,仿真时长为6 s,观测线路34条。

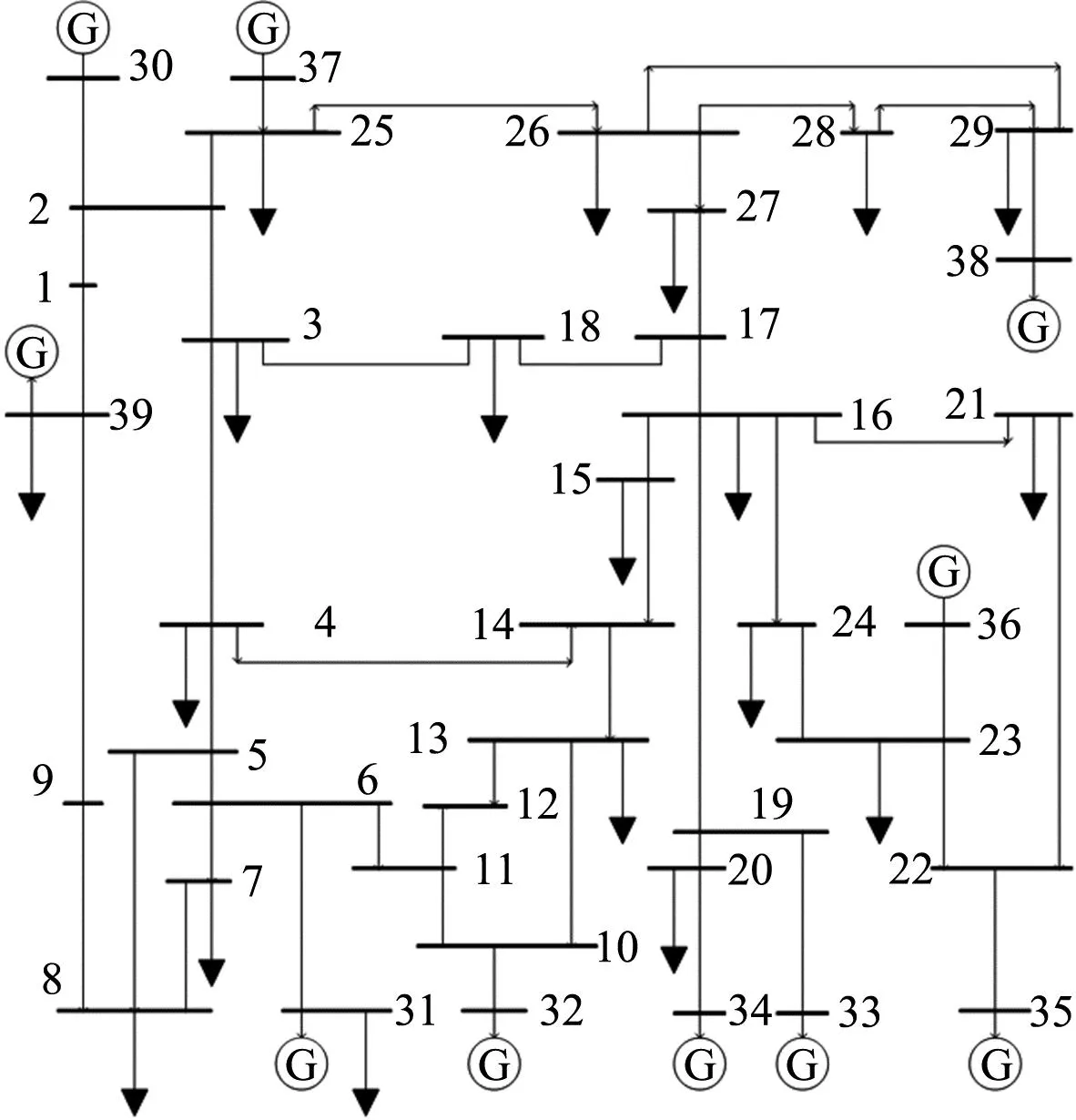
图6 IEEE39节点系统结构

算例1:线路4-14母线4侧0.18 s发生三相短路故障,0.4 s切除线路(系统稳定)。

共有24条线路存在振荡中心,选取了其中3条振荡线路,线路排序如表1所示。线路8-9振荡次数最多、电压最低。

表1 线路4-14三相短路故障振荡线路统计

线路8-9和线路5-6振荡中心位置和电压幅值变化曲线如图7所示。

(a)线路8-9

算例2:线路3-18母线3侧0.18 s发生三相短路故障,0.4 s切除线路(系统失稳)。

共有21条线路存在振荡中心,选取了其中3条振荡线路,线路排序如表2所示。

表2 线路3-18三相短路故障振荡线路统计

线路8-9和线路1-2振荡中心位置和电压幅值变化曲线如图8所示。线路1-2、8-9为重要输电通道,线路8-9发生三相短路后,发生潮流转移,导致线路1-2和线路8-9功率振荡。

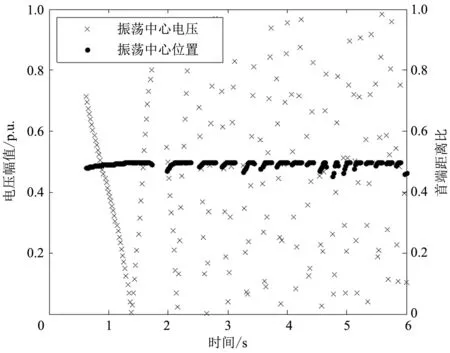
(a)线路8-9

4.2 南方电网实际系统算例

以贵州六盘水电网为研究对象,进一步验证本文所提方法有效性。电网结构如图9所示,总装机约2225 MW,水电风电等新能源装机约640 MW(占比约28.7%),负荷水平在790～1200 MW,电力外送功率较大,送端电网特征明显。当重要输电通道发生三相短路故障切除后,系统潮流短时间内大量转移,易发生暂态稳定性问题。采用PSD-BPA软件时域仿真结果模拟广域测量数据,运行方式为某年丰大方式。仿真步长为0.02 s,仿真时长为4 s,观测线路16条。

图9 六盘水电网结构

算例1:盘县-双龙线(盘县电厂侧)0.18 s三相短路故障,0.3 s切除线路(稳定)。

共有11条线路出现振荡,选取了其中3条振荡线路,线路排序如表3所示。

表3 盘双线三相短路故障振荡线路统计

线路盘县-台沙和威宁-水城振荡中心位置和电压幅值变化曲线如图10所示。

(a)盘县-台沙

盘台和盘双线作为盘县电厂外送电力通道,当盘双线路发生三相短路故障切除后,外送功率转移至盘台线,发生明显的功率振荡现象。

算例2:盘县-台沙线(盘县电厂侧)0.18 s三相短路故障,0.3 s切除线路(失稳)。

共有12条线路出现振荡,选取了其中3条振荡线路,线路排序如表4所示。

表4 盘台线三相短路故障振荡线路统计

线路六枝-双龙和盘县-双龙振荡中心位置和电压幅值变化曲线如图11所示。当盘台线故障切除后,盘县电厂外送功率转移至盘双线、六双线,超出线路功率限额,系统暂态失稳,振荡明显。

(a)六枝-双龙

4.3 算例小结

根据算例分析,电网重要输电通道发生三相短路故障等大扰动后,重要断面或线路存在明显振荡,其振荡中心的分布和变化规律呈现如下特点:

a. 在系统振荡过程中,部分线路会出现明显的振荡特征,可选择出现振荡中心次数较多、电压较低的线路作为重点观测线路;

b. 系统稳定时,线路出现振荡中心次数较少,振荡中心电压也较高;系统失稳时,线路出现振荡中心次数较多,且振荡中心电压较低,接近于零;

c. 振荡中心电压的高低反映了系统的安全稳定状态,振荡中心电压越低,系统的稳定水平越差;

d. 可根据振荡中心联络断面电气量进行进一步暂态稳定性判定,避免对全网数据的依赖。

5 结语

本文重点研究了新能源接入电网发生严重故障后、暂态过程中重要断面存在振荡中心的识别判据、振荡中心的特点以及振荡中心的位置变化规律。利用广域测量大数据全局性和实时性的特点,提出了一种基于广域测量大数据的电力系统振荡中心识别方法,该方法能够为基于电力大数据的新型电力系统安全稳定分析确定系统振荡中心。通过IEEE39节点系统和中国南方电网实际系统算例分析,验证了本文所提方法的有效性及实用性。