基于MI-LSTM输电线动态参数修正的电力系统可用输电能力计算
秦 爽,朱秋成,施宇丹
(1.国家电网有限公司东北分部,辽宁 沈阳 110181;2.四川大学建筑与环境学院,四川 成都 610065;3.华北电力大学国际教育学院,河北 保定 071003)
0 引言
电力系统可用输电能力(available transfer capability,ATC)是衡量电力系统区域间进一步可靠传输电能的能力[1]。ATC计算值高于实际值会导致电力系统发生网络阻塞、电压越限、线路超出热稳极限等问题,威胁系统安全;ATC计算值低于实际值会导致电力系统资源利用不足,能源消纳能力下降等问题。因此,准确、高效的ATC计算有助于提升电力系统运行的安全稳定性,为区域间电能交易提供重要的参考信息[2]。
影响ATC计算的不确定性因素主要分为2类,一类是新能源厂站引入电力系统中造成的出力不确定性;另一类是电力系统实际运行中的参数不确定性。文献[3-4]考虑了新能源出力不确定性对ATC的影响,分别提出了新能源出力波动及新能源发电装置断网离网时ATC的计算方法。灵活交流传输系统中潮流控制器对潮流方向的实时控制及大量电力电子设备引入电力系统对传统潮流模型的参数改变,会通过参数不确定性引起潮流的变化,进而影响ATC的计算准确性,已有相关学者针对上述问题对ATC计算模型进行优化[5-6]。
引起电力系统潮流计算中参数变化的原因不仅包括电力电子器件的引入,环境及气象变化也会造成参数的动态变化。文献[7]建立了复杂天气的电力系统ATC计算模型,该模型通过计算不同天气场景下的设备故障率,探究了设备故障造成的参数及拓扑变化对ATC潮流计算的影响。在电力系统实际运行中,环境及气象除了影响设备运行外,还造成了输电线参数的不确定性。因此,ATC计算也应考虑环境影响下的输电线参数的动态变化。一方面,天气与环境因素造成输电线电阻、电抗和电纳参数发生动态变化,进而影响网络的潮流分布;另一方面,天气和电阻的动态变化造成传输线的载流能力和最大热载流极限发生动态变化。文献[8]验证了环境与气象的变化会造成输电线路电气参数的动态变化。输电网络架空线分布范围广,每条线路的参数在不同地域和不同季节受到的微气象的影响程度不同,如何考虑时空特异性对输电线参数进行合理的动态估计仍需进一步研究。文献[9]提出风速、环境温度、日照影响架空线热载流量,准确评估最大载流量应使用动态热定值。动态线路潮流极限(dynamic line rating, DLR)通过环境等因素对输电线最大载流能力进行计算,可以实现对线路最大载流量的动态评估,目前已有学者将DLR应用到ATC计算中[10]。文献[11]通过神经网络技术在不同气象场景下实现DLR的动态估计,该估计方式将气象特征作为输入,静态参数对应的理论极限值作为输出,但并未充分考虑动态参数和时空环境因素对DLR的影响。
针对上述问题,本文提出一种基于MI-LSTM输电线动态参数修正的可用输电能力计算方法。首先利用互信息(mutual information, MI)量化不同时空区域下环境因素对输电线参数的影响程度,通过量化矩阵对环境特征进行动态修正。将环境特征作为输入,利用长短期记忆神经网络(long-short-term memory, LSTM)对输电线参数进行并行预测[12]。利用动态参数进行潮流计算和动态线路潮流极限修正,最终实现ATC的动态计算。所提方法利用辽宁电网实测数据在IEEE14节点系统中进行仿真验证。
1 考虑环境影响程度时空变化的动态参数估计模型
1.1 环境因素影响程度的时空变化特性
电力系统输电线路参数受多种因素影响,影响输电线参数的环境及气象因素具有较强的时空特性,科学和客观的量化环境因素对参数变化的影响程度尤为重要。本文引入信息熵理论中的MI值来实时量化各类环境因素对参数的影响程度[13]。MI值可以有效地度量特征数据之间的线性及非线性关联,在量化过程中不需要预知数据分布,因此,可以利用MI量化不同时空状态下环境数据对输电线参数的影响程度大小。
设定X为某条输电线路在特定时间区间内某种环境特征的数据集,Y为该种特征数据所对应的某一种参数值集合。特征数据X的自信息计算公式如式(1)所示。
(1)
式中:p(x)为X的概率密度函数。
环境特征数据X和对应参数Y之间的MI值计算公式如式(2)所示。
(2)
式中:pXY(x,y)为随机变量X和Y的联合概率密度函数;pX(x)为随机变量X的边缘概率密度函数;pY(y)为随机变量Y的边缘概率密度函数。本文中环境因素X及线路参数Y为离散变量,式(2)改写为
(3)
环境特征X对线路参数Y的影响越大,2个变量间的相关性越强,MI值越大,环境特征X对线路参数Y没有影响,则2个变量相互独立,MI值为零。由此,可通过MI值实现不同时空尺度下环境因素对线路参数影响程度的量化。
1.2 基于MI-LSTM的动态参数估计模型
输电线路参数的动态变化受时空因素影响,本文选用LSTM模型,对时空因素影响下的动态参数进行预测。但LSTM模型中的权值共享机制不能随时间推移及天气变化去动态修正环境因素的输入特征对输出参数的影响程度,忽略了环境因素的影响程度是随时间的改变而变化的这一特性。为了弥补LSTM模型权值共享结构的时不变性,本文利用MI量化不同时刻下环境因素对线路参数的影响程度,将量化值作为系数与环境因素变量相乘,进而实现对输入特征权值的动态修正。输入特征权值修正前后的动态参数预测结构对比如图1所示。

图1 LSTM及MI-LSTM动态参数预测结构对比
以t时刻某条线路的实时参数预测为例,选取t-n至t-1时刻的n组历史数据作为训练集。训练集输入矩阵如式(4)所示。
(4)
式中:z为环境因素输入特征的种类数。
训练集输出矩阵如式(5)所示。
(5)
利用上节提到的环境因素影响程度量化方法,通过历史数据计算不同季节不同天气下,每个训练时刻各类环境因素对3种参数影响程度的MI值。以电阻参数预测为例,其MI值矩阵计算方法如式(6)所示。
(6)
训练集MI矩阵中每个元素都由与该时刻对应季节及天气相同时刻的历史数据计算得到。MI矩阵中包含了不同维度下输入特征对某种参数的影响程度信息,通过横向时间维度对比可以反映同类输入特征在不同时刻下的影响程度变化,而纵向种类维度对比可以反映不同类型的输入特征在同一时刻、同一季节天气下的影响程度差异。以电阻参数估计为例,利用MI修正训练集输入,其计算过程如式(7)所示。
I′=I×MIR
(7)
式中:×是对2个矩阵进行哈达马积运算,即将2个矩阵对应位置的元素分别相乘;I′为计及影响程度变化的环境因素特征输入矩阵。

(8)
滚动修正时序神经网络预测模型的输入矩阵,得到t时刻实时参数预测输入矩阵I″。
(9)
将矩阵I″作为输入代入经过训练的时序预测模型中,即可得到t-n+1至t时刻电阻参数的预测值,其中t时刻预测值即为实时电阻参数预测值。
综上,可实现对动态参数特征输入的动态修正,使参数预测模型可以动态追踪输入特征影响程度的时序变化。单条输电线路MI-LSTM动态参数估计模型的整体流程如图2所示。

图2 单条输电线路MI-LSTM动态参数估计流程
2 考虑输电线路参数动态变化的ATC计算模型
ATC是指在现有传输合同的基础上,实际的物理传输网络中剩余的、可用于商业的输电能力[14]。ATC计算是在保证系统安全可靠运行前提下,计算电力系统区域间或点对点之间可能增加的最大输送功率。本文重点从环境因素影响下的输电线参数动态变化的角度出发,探究参数变化引起的潮流变化、最大载流极限变化对ATC计算的动态影响。
2.1 线路参数修正

(10)

2.2 动态潮流极限修正
影响线路传输容量的关键因素为导体的热稳定极限,导体的温度主要取决于导体载流量、导体横截面积及电阻、导体所处环境条件3个方面。因此,本文通过输电线动态电阻及环境因素计算线路的热容量极限,进而实现对输电网各线路动态潮流极限的实时修正。线路潮流极限以最大传输电流进行衡量,其计算式为
(11)
(12)
(13)
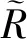
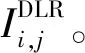
考虑输电线动态参数变化的ATC计算流程如图3所示。

图3 考虑输电线动态参数变化的ATC计算流程
3 算例分析
3.1 算例系统及数据
本文算例以IEEE14节点输电网络为基础进行仿真验证[15]。IEEE14节点系统共有5个发电机节点,20条输电线路,拓扑结构如图4所示。其中,区域A为供电区域,包含发电机节点1和负荷节点5;区域C为受电区域,包含负荷节点13及负荷节点14。系统的电压等级为110 kV,装机容量为500 MW。在计算中假定负荷节点有功的上、下限标准为100 MW和0 MW;供电区域发电机组最大允许出力为300 MW;负荷节点无功上、下限标准为100 Mvar和0 Mvar;电压上下限依据电力系统安全基准进行设定。

图4 IEEE 14节点输电网系统接线图
算例采用东北某地区110 kV输电系统近3年的线路参数量测数据库、气象数据库及环境因素量测数据库进行动态参数估计模型的验证,并利用实际网络动态参数及环境因素数据在IEEE 14节点输电网络上进行ATC改进计算模型的仿真及验证。
3.2 MI-LSTM动态参数估计模型可行性验证
为探究MI-LSTM改进动态参数估计模型的估计准确度,算例选取线路1-5进行参数估计算法的可行性验证。由于实际运行数据中,环境因素对输电线路电抗影响程度不大,动态电抗参数变化不明显,因此,算例选取线路1-5的动态电阻、动态电纳进行估计及对比验证。分别从夏季和冬季数据库中各选取天气变化较为剧烈的一天,对其进行间隔为1 h的动态参数滚动预测。夏季选取日1—22时为晴天,22—24时为降雨天气;冬季选取日1—15时为晴天,15—24时为降雪天气。电阻动态参数在夏季选取日和冬季选取日的估计结果如图5和图6所示。

图5 夏季某天电阻动态参数估计结果对比

图6 冬季某天电阻动态参数估计结果对比
由电阻动态参数估计结果可知,LSTM估计模型利用动态参数的时序关联性,可以整体上跟随真实参数的变化趋势。然而,当一些对电阻影响程度较小的环境因素发生较大变化时,如夏季暴雨天气湿度突然增加、日照强度突然减少;冬季雨雪天气风速突然变大、日照突然减少时,LSTM的权值共享特性会导致学习模型过度参考非重要环境影响因素,最终导致预测精度偏低。MI-LSTM模型通过对环境数据输入权值的修正,充分考虑各类天气状态下的影响变化,进而提高估计精度。经计算可知,上述估计时段LSTM模型夏季平均估计误差为0.245%,冬季平均估计误差为0.107%;MI-LSTM模型夏季平均估计误差为0.048%,冬季平均估计误差为0.032%。夏季选取日输电线动态电纳参数的估计结果如图7所示。
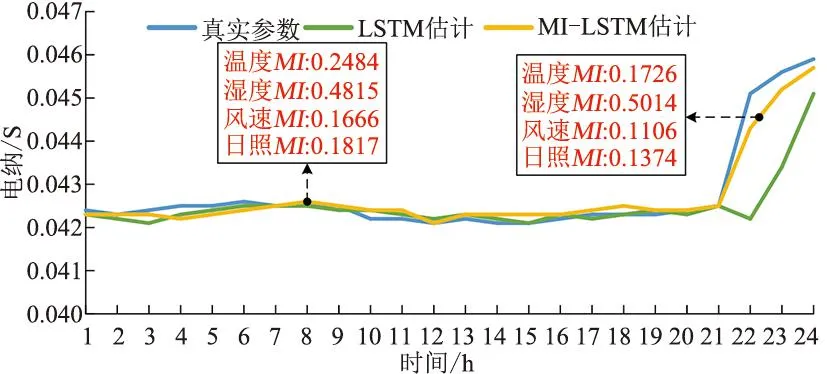
图7 夏季某天电纳动态参数估计结果对比
由图7可知,在夏季晴天时段LSTM估计和MI-LSTM估计准确度较高。在暴雨时段,空气湿度骤增,LSTM无法及时响应湿度的变化,因此估计准确度降低,而MI-LSTM通过MI动态修正输入特征权值,使估计模型及时响应湿度变化,提高了电纳估计精度。
综上所述,MI-LSTM模型可以实时追踪天气变化,动态修正输入特征权值,提升动态参数估计的准确度。
3.3 含动态参数修正的ATC计算
为探究动态参数及动态线路潮流极限引入后输电网可用传输容量的变化情况,分别在夏季及冬季各选取30天,计算每日中午12时的ATC。计算结果如图8所示。

(a)夏季ATC
算例选取了原始负荷需求较为接近的2天(夏季的第15天与冬季的第8天),分别比较在不同参数下ATC计算值的大小。由数值结果对比和曲线对比可知,夏季采用动态参数计算的ATC结果略小于采用静态参数计算的ATC结果,引入DLR后的ATC计算结果与静态参数计算结果相差较大,其计算值远小于静态参数计算结果;冬季采用动态参数计算得到的ATC结果与静态参数得到的参数结果相差不大,引入DLR后的ATC计算结果与静态参数计算结果相差较大,其计算值大于静态参数计算结果。
这是因为夏季环境温度较高,日照强度较大,输电线路动态电阻值偏大,各类动态参数波动性受环境影响波动性较大,导致传输线路更易达到热稳极限,采用动态电阻及环境计算求得的DLR约束变低。因此,使用动态参数的ATC计算值偏小,使用动态参数和DLR的ATC计算值远小于使用静态参数的ATC计算值。而冬季环境温度较低,动态电阻值相对减小,线路载流能力提升,不易到达热稳极限,DLR约束变高。因此,使用动态参数和DLR的ATC计算值要高于使用静态参数的ATC计算值。
4 结语
本文建立了基于输入特征影响程度量化的输电线路MI-LSTM动态参数估计模型,并基于参数估计模型建立了考虑输电线路动态参数及动态传输极限的ATC计算模型。应用东北地区实际天气数据及输电线参数数据,对环境因素互信息熵进行量化计算,对环境变化影响下的输电线路动态参数进行计算,对计及动态参数变化和线路动态传输极限变化的电力系统ATC进行求解。
计算结果表明,利用互信息熵可以量化环境因素在不同时空下的影响程度;利用影响程度的量化值修正特征输入,可提高动态参数的估计精度;采用动态参数和动态潮流极限可以更加准确评估系统ATC,更加贴近运行实际,为电力市场参与者和电网运行人员提供更准确的电网信息。

