数形结合百般好

严予瑢

今天是平凡得不能再平凡的一天，我们上着一节与往日“无异”的数学课。

交流环节，老师布置了一道题：

在数轴上，点A、B分别表示a、b，计算下列情况下点A、B之间的距离：a=1，b=5；a=0，b=5；a=1，b=-5；a=-1，b=-5。你能发现点A、B之间的距离与数a、b之间的关系吗？

我看到题目后，先把每组数分别在数轴上表示出来，如下图所示：

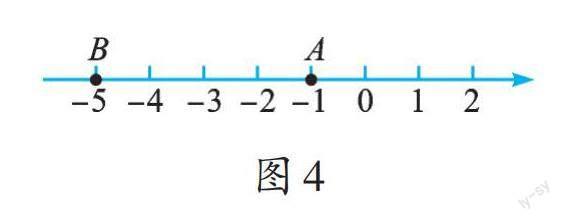
图1中，AB=b-a=5-1=4；图2中，AB=b-a=5-0=5；图3中，AB=a-b=1-（-5）=6；图4中，AB=a-b=（-1）-（-5）=4。

通过观察，我发现，AB=a-b或b-a。因为互为相反数的两个数的绝对值相等，AB的长度为非负数，所以AB=[a-b]。我知道了：已知数轴上两点表示的数，利用这个公式可以求出这两點之间的距离。

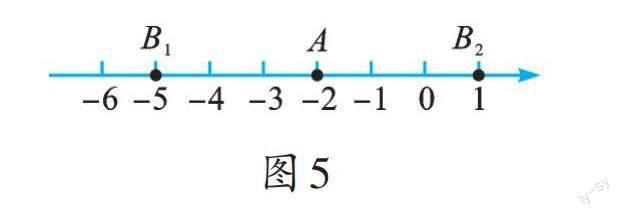
如数轴上，点A表示的数是-2，AB=3，若表示点B的数记为x，则[x-（-2）]=3。没有学过含绝对值的方程，怎么求x的值呢？这时，我想到老师讲过，绝对值表示距离，如到原点的距离等于3的点有两个，一个在原点的左边，另一个在原点的右边，所以到点A的距离等于3的点也有两个，一个在表示-2的点的左边，即x=-5，另一个在表示-2的点的右边，即x=1（如图5）。所以，我又发现：某点到一个定点的距离等于一个正数时，画数轴能直观地找到两个这样的点。

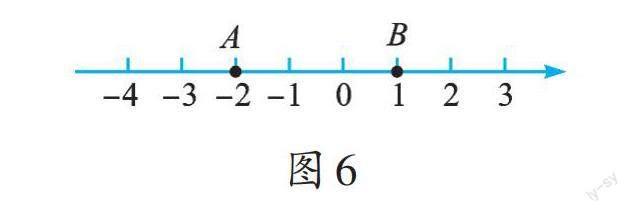
类比可知，[x-1]表示x到1的距离，[x-（-2）]表示x到-2的距离。若已知[x-（-2）]+[x-1]等于一个正数，怎么求x呢？我在数轴上标出分别表示-2、1的两个点，观察数轴：这两个点将数轴分成3部分——表示-2的点的左边部分，表示-2与表示1的两点之间的部分（包括表示-2、1的两个点），表示1的点的右边部分（如图6）。我惊喜地发现：在x变化的过程中，[x-（-2）]+[x-1]有最小值，且最小值是3；当[x-（-2）]+[x-1]取一个大于3的数时，满足条件的点也有两个。

如果将3个绝对值相加呢？如[x-（-2）]+[x-1]+[x+1]，小伙伴们不妨动手试试，你发现了什么？

“数形结合百般好”。从1个绝对值，到2个绝对值，再到3个绝对值……研究的问题越来越复杂，但只要我们抓住问题的本质，利用好数轴，就能轻松地解决问题。

教师点评

数形结合是解决数学问题的有效思想，“数缺形时少直观，形少数时难入微”。小作者借助已有的学习经验，积极思考，主动类比探究，从数量特征联想到几何特征，把数的问题转化为形的问题。同时，小作者还发现变化中不变的量，这是个了不起的发现！

（指导教师：严亚琴）