面向新型配电系统电压支撑的微电网供电性能提升控制策略

李秉宇，杜旭浩，郭小凡，刘 超，程麟舒

(1.国网河北省电力公司电力科学研究院，河北 石家庄 050021；2.北方工业大学，北京 100144）

0 引言

新型配电网系统是在传统配电网基础上，通过微电网大规模集成风/光/储等多种电源，实现对负荷高可靠供给的配用电系统。新型配电网系统是实现“双碳”目标，有效促进清洁能源开发利用和落实大气污染防治措施的重要举措，具有鲜明的技术革命特征。由于高渗透率分布式能源组成的微电网接入配电网，导致微电网母线电压的动态特性将会直接影响新型配电网系统的稳定性，因此，保证微电网的母线电压性能是维持新型配电网安全可靠运行的基础[1]，[2]。

由于新型配电系统内部分布式电源出力的不确定性、负载投切以及微电网系统自身低惯量的特点，用户侧的电能使用受到了较大的影响，在运行过程中容易造成母线电压偏差、三相电压不平衡、谐波等电能质量问题，从而导致系统供电性能下降。为此，国际电工委员会(IEC）已经建立了多项标准，为用户侧电能质量的治理提供了发展契机[3]。当微电网并网时，大电网可以稳定其电压和频率，提升其抗扰能力。当微电网在孤岛模式下运行时，其交流母线电压由众多微源共同支撑，这些微源主要通过双向AC/DC换流器(逆变器）进行控制。因此，通过对逆变器进行合理的控制能够提升用户侧的供电性能。

在工业实践中，PID(Proportion-Integral-Derivative）控制运用最为广泛，设计方法也有很多种，但其闭环稳定性仍然是一个须要深入研究的问题。另外，PID控制对象的稳定域难以在线确定，限制了控制性能[4]。尤其是在各种扰动出现的情况下，难以获得理想的动态特性，严重时会使得系统崩溃。文献[5]针对微电网功率和电压波动问题，提出了一种基于扰动观测器的补偿控制策略，并与传统PID控制进行了对比，提升了系统的鲁棒性，但其电压幅值在投切负载时仍有较大的波动。文献[6]将负载电流作为扰动，提出了一种基于扰动观测器的电流前馈控制方法，在无须增加额外的传感器的情况下，实现了对输出电压波动的抑制，并给出了普适性的参数计算方法。文献[7]提出了一种基于卡尔曼滤波的控制方法，将逆变器进行简化，从而提高了控制器的执行效果，提高了输出电压的鲁棒性。文献[8]，[9]提出了基于非线性干扰观测器的电压控制方法，可以有效地抑制母线电压的波动，但逆变器存在dq轴耦合的关系，会使得系统变得十分复杂。文献[10]提出了自抗扰控制，将影响系统控制的不良因素视为总扰动，并进行动态补偿，与传统PI控制相比，在跟踪和抗扰性能方面都有了明显的提升。文献[11]提出了一种鲁棒分散式电压控制结构，将微电网的电压控制问题转化为一个凸优化问题，成功抑制了负载投切对系统产生的影响。

为了提升新型配电系统微电网中逆变器输出电压的暂态响应速度、抗干扰能力以及新型配电系统的供电性能，本文通过对新型配电系统中的逆变器进行线性化建模，结合状态反馈和线性二次最优控制算法，设计了基于LQR的控制器，该控制器的控制目的更为明确，参数设计简单且能够更有效地提升系统的暂态响应速度。在对逆变器输出电压进行分析后，在LQR控制器的基础上，提出了一种基于扰动残差生成器性能提升的控制结构，该结构基于鲁棒二重互质分解和尤拉参数化理论，无需额外的电压电流传感器。同时，也无须知道具体的扰动形式，在扰动发生时，只须通过残差生成器输出的残差驱动动态性能提升控制器，即可抑制扰动信号对系统的影响，增强系统的抗干扰能力。

本文在MATLAB/Simulink中设计了负载投切、三相不平衡负载以及谐波负载实验来验证所提控制策略的正确性和有效性。

1 新型配电系统下逆变器LQR控制策略

1.1 新型配电系统下三相逆变器的数学模型

逆变器作为新型配电系统中常见的电力电子变换器，其拓扑结构如图1所示。图1中：udc为直 流 侧 电 压；ui，abc为 交 流 测 三 相 电 压；iL，abc为 交 流测 电 感 电 流；uo，abc，io，abc分 别 为 交 流 侧 负 载 电 压、电流；Rf，Lf分别为交流侧滤波电感等效电阻、电感；Cf为交流侧滤波电容。

图1 三相电压型逆变器拓扑结构Fig.1 Three-phase voltage inverter control structure

将三相静止坐标系转换到dq旋转坐标系后，选 取 负 载 电 压uod，uoq，电 感 电 流iLd，iLq为 状 态变量，逆变桥输出电压uid，uiq为输入变量，负载电流iod，ioq为 扰 动 输 入d，uod，uoq为 系 统 输 出，可 以 得到线性化三相逆变电路的状态空间方程为

式 中：ω为 基 波 角 频 率；x=[iLd，iLq，uod，uoq]T为 系 统的状态变量，分别为派克变换后dq轴电感电流和输出电容电压；y=[uod，uoq]T为系统输出变量。

1.2 线性系统最优控制

在现代控制理论中，状态反馈可以全面地反映系统的内部特性，通过极点配置，可以得到良好的动态性能[12]。但是由于加载后的三相逆变电路为零型系统，根据终值定理，输入阶跃信号时，输出电压会产生稳态误差，影响系统的稳态运行[13]。因此，需要通过增加一个积分型控制器来消除稳态误差。此外，没有必要使用比例积分控制器来代替积分控制器，因为这会使得系统引入一个新的零点，影响系统的动态响应[14]。三相电压型逆变器控制结构如图2(a）所示。

图2 三相电压型逆变器控制结构Fig.2 Three-phase voltage inverter control structure

图2中：k1，k2为状态电流电压反馈参数；k3为积分参数；e为给定电压与实际输出电压的差值；uo*为逆变电路的给定输入。

通常利用Riccati方程求解一个常值正定矩阵P来得到最优控制输入ui*。通过选取合适的误差加权矩阵Q和控制信号的加权矩阵R的值，带入Riccati方程，即可得到最优控制参数k1，k2，k3的值。ui*的求解如式(2）所示。

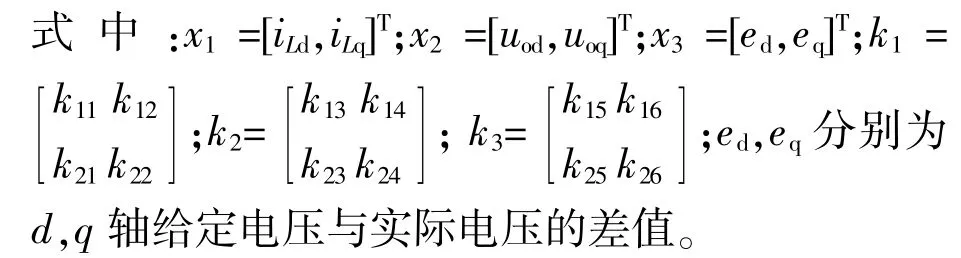
为了求解最优控制输入ui*，可以重新定义状态变量，令：

在不考虑扰动的情况下，式(1）可以变换为如下新的状态方程：

重新定义状态变量后的系统控制框图如图2(b）所示，新系统的性能指标可以表示为

由式(4）可知，控制器参数求解的问题被转化为一个LQR的调节问题，只须要选取合适的Q和R的值，就可以得到优化控制参数矩阵K，得到期望的系统性能。

通过LQR控制器可以提升新型配电系统内电压的暂态响应速度以及稳态精度，但是在系统稳定运行的过程中，投切负载、加入三相不平衡负载或是加入非线性负载仍然会使得母线电压出现较大的波动，影响系统的稳态运行。因此，为了进一步提升系统的抗干扰能力，在原有LQR控制器的基础上设计了一个基于扰动残差生成器的性能提升结构，提取残差值并补偿到输入端。根据叠加原理，补偿信号与扰动信号在输出端相加为零，可以有效地抑制逆变器输出电压的暂升暂降或者畸变等，提升逆变器的抗扰能力和可靠性。

2 基于扰动残差生成器的新型配电系统下逆变器动态补偿性能提升控制

2.1 新型配电系统内电压扰动分析

一般情况下，新型配电系统下的理想电压可以表示为[15]

式中：U1为基波电压幅值；θ1为初相角。

系统内部扰动被分为两类：①基波电压的幅值U1发生变化，其中包括电压暂降、过电压、欠电压以及波动与闪变等；②加性扰动，包括谐波、三相不平衡、冲击脉冲电压等。

三相逆变器的桥臂电流转化到dq坐标系下的表达式如式(6）所示。

由式(6）可知，当输出电压出现波动时，逆变器输出电流iod，ioq相当于扰动输入。当电路进行负载投切时，dq轴输出电流表达式为

式 中：iod1，ioq1为 基 波 电 流 幅 值；Ipd，Ipq为 波 动 电 流幅值；l(t-tp）为阶跃函数；tp为负载投切时刻。

根据式(7）可知，微网逆变器投切负载后对新型配电系统内的电压影响在dq坐标系下主要表现为阶跃扰动。

当逆变器接入的负载为三相不平衡负载时，根据对称分量法，可以将相电压分解为正、负、零序电压，忽略谐波分量后，三相电流在dq坐标系下的输出表达式为[16]

式中：ioo为零序电流；分别为输出正、负、零 序 电 流 幅 值；θ+，θ-，θo分 别 为 正、负、零 序 电流初相角。

由式(8）可知，新型配电系统内部不平衡电压在dq轴表现为直流分量和2倍工频交流负序分量的叠加。

当逆变器带非线性负载时，新型配电系统内的电压可表示为基波电压与谐波电压之和的形式。其中，正序谐波电压将以6k+1(k为正整数）次谐波的形式出现在dq轴中，负序谐波电压将以6k-1次谐波的形式出现在dq轴中，零序谐波电压都为零[17]。

2.2 性能提升理论

如果对于一个真有理传递函数G(s），可控可观，并外加控制器K(s）保持稳定，传递函数G(s）可 用RH∞上 的 左 互 质 矩 阵M^(s），N^(s）和 右 互 质矩 阵M(s），N(s）表 示：

同理控制器K(s）也可用RH∞上的左互质矩阵X^(s），Y^(s）和 右 互 质 矩 阵X(s），Y(s）表 示：

存 在M(s），N(s），M^(s），N^(s），X(s），Y(s），X^(s），Y^(s）∊RH∞，满 足Bezout方 程，即：

通过引入矩阵Qc(s）可得到稳定化控制器的参数化形式，即尤拉参数化，如式(12）所示[18]。

Steven Ding深入研究了尤拉参数控制理论并 推 导 出 定 理1[19]，[20]：给 出 被 控 对 象G(s）的 控 制回路和一个由现有控制器K(s）提供的控制信号u1，该控制环内部稳定，则所有内部稳定的控制器可以被参数化为

式中：u1为原控制器的输出；u为实际控制器的输出；Qc为补偿信号的传递函数矩阵；r为残差信号。

控制器性能提升结构如图3所示。当原系统稳定时，加入性能提升控制器后系统仍然稳定。当发生未知扰动时，通过残差生成器可以得到观测电压与实际输出电压的差值，也就是残差信号。然后通过Qc进行反向补偿，抵消扰动d对系统电压造成的暂态影响。残差生成器的结构如式(14）所 示。

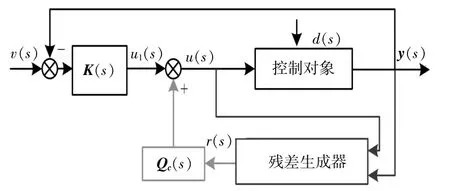
图3 基于鲁棒残差观测器的性能提升控制框架Fig.3 Performance improvement control framework based on robust residual generator

式中：L为观测器增益矩阵；x^为重构的状态向量；y^为重构的输出。

2.3 新型配电系统下基于LQR的逆变器性能提升控制

2.3.1电压性能提升控制

控制器性能提升结构独立于原控制器，且不影响原系统的稳定性。令ex=x-x^，联立式(1），(14）可以得到如式(15）所示的逆变器残差生成器计算表达式。

式中：ex为残差生成器的状态向量；d为残差生成器的输入。

残差生成器可以等效为一个以扰动d作为输入，残差r作为输出的系统。新型配电系统内基于LQR控制器的三相逆变器解耦后的d轴性能提升结构如图4所示。图4中：uod*为d轴的输入参考电压；uod为d轴的输出电压；iLd为电感电流；Io为扰动输入；rd为d轴残差生成器的输出残差信号；Qc为电压补偿信号的传递函数；urd为电压补偿输出；uid为控制器输出。

图4 解耦d轴性能提升结构Fig.4 Decoupling d-axis performance improvement structure

系统处于稳态时，在某一时刻加入扰动电流Io，通过梅森公式可以求得扰动作用下系统的传递函数，并求得等效开环传递函数。通过开环传递函数可以发现，整个配电系统的电压会受到扰动的影响出现短暂波动。

本文通过增加扰动残差生成器和性能提升控制器Qc来实现逆变器的性能提升，从而达到提升新型配电系统供电性能的目的。当没有扰动Io时，残差生成器的输出为0，Qc的输出补偿电压信号为0。当出现扰动电流Io时，残差生成器会迅速输出一个残差信号rd，再经过补偿传递函数矩阵Qc输出一个补偿信号urd，根据叠加原理，urd作用于被控对象与Io作用于被控对象的输出和为零，可以实现扰动的抑制。

2.3.2二次补偿控制

由图5可知，当扰动电流Io出现时，补偿控制信号urd在补偿扰动的同时，也会对电感电流iLd造成影响，而电感电流会通过反馈系数k2反馈到控制回路中，使得控制信号uid发生变化，造成系统的二次扰动。因此，为了避免控制器带来的二次扰动，本文设计一个二次补偿控制器H来抵消控制回路的二次扰动，补偿结构如图5所示。

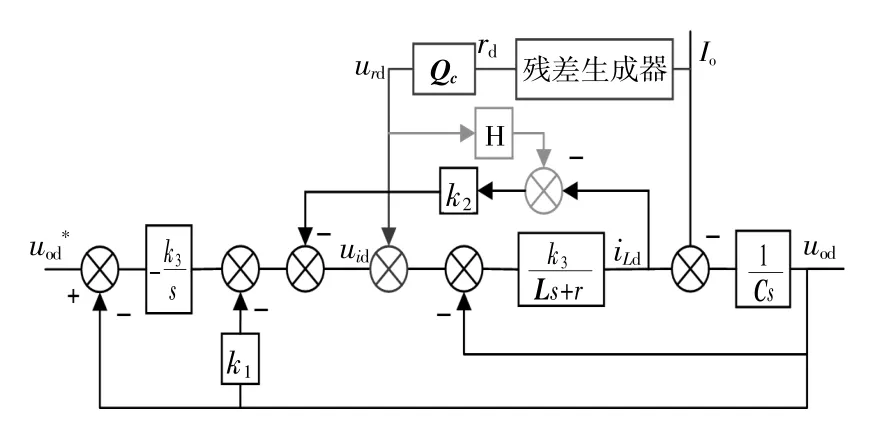
图5 二次补偿后系统性能提升控制结构Fig.5 System dynamic compensation structure after secondary compensation

基于上述的理论分析推导，得到了完整的基于线性二次最优控制的逆变器性能提升架构以及需要求解的参数，扩展到双轴的控制结构见图6。

图6 新型配电系统下三相逆变器性能提升结构Fig.6 Performance improvement structure of three-phase inverters in new distribution systems

3 新型配电系统下的性能提升控制器求解

3.1 性能提升控制器Qc求解

根据上述理论推导以及模型匹配理论[22]，得到性能提升控制器的模型匹配结构，如图7所示。图7中：Gyd为扰动直接作用于系统的传递函数矩阵；Grd为残差生成器的传递函数矩阵；Gp为Qc输出的补偿控制信号；ur为系统输入的传递函数矩阵。

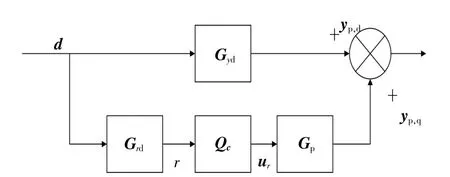
图7 模型匹配结构Fig.7 Model matching structure

根据线性系统的叠加原理，当扰动作用于控制对象时，会产生一个扰动输出yp，d，而性能提升控 制 器 也 产 生 一 个 补 偿 输 出yp，q，当yp，d+yp，q=0时，理论上就可以抵消任意扰动对系统的作用。Qc的求解过程如式(16）所示。

Gyd输 入 为d，输 出 为yp，d，状 态 空 间 表 达 式 为

Grd输入为d，输出为r，状态空间表达式如式(15）所示。根据系统维数，可知观测器的增益矩阵是一个4×2的矩阵，因此设观测器增益矩阵为

Gp输 入 为ur，输 出 为yp，q，状 态 空 间 表 达 式 为

xp=[iLdiLquoduoq]T为 状 态 变 量 ，ur=[urdurq]T为补偿电压输入。

根据式(16），通过矩阵运算，可以解得性能提升控制器Qc的传递函数矩阵，经过化简后可以得到矩阵元素最简表达式。

由式(19）可知，分子阶次大于分母阶次，根据线性系统控制原理，必须对分母进行补偿，使分母阶次大于等于分子，由此可得最简Qc的矩阵表达式为

式中：η为补偿系数。

3.2 二次补偿求解

只考虑逆变器单轴，不考虑外环控制器时，通过求解传递函数可以得到：

根据式(16）可以解得：

当考虑到外环控制器时，电感电流的反馈会给系统造成二次扰动，为了消除二次扰动对系统的影响，必须进行二次补偿。根据图6的结构，传递函数可以表达为

联立式(22）和式(24）可以得到H的求解表达式。

式中：G′yd为扰动直接作用于整个系统的传递函数；Q′c为 整 个 系 统 补 偿 信 号 的 传 递 函 数；G′p为Q′c输出的补偿信号作用于整个系统的传递函数。

扩展到三相逆变器双轴解耦模型可以得到最终二次补偿的表达式。

式 中：ird，irq分 别 为d，q轴 二 次 补 偿 输 出；urd，urq分别为d，q轴电压补偿输出。

4 实验验证

为了验证本文所设计的新型配电系统下基于线性二次控制和残差生成器的逆变器性能提升架构的效果，设计不同种类的实验，并利用MATLAB/Simulink仿真验证本文所提控制策略的合理性。实验参数设置如表1所示，供电的电能质量国家标准如表2所示。

表1 仿真参数Table 1 Simulation parameters

表2 供电电能质量国标Table 2 National standard for power quality

4.1 阶跃扰动实验

投切有功功率为15 kW，无功功率为8 kVar的负载，保证线路其他参数不变，通过MATLAB/Simulink仿真，得到系统d轴电压波形，如图8所示。逆变器输出三相电压如图9所示，0.1 s投入负载时，在只有传统PI控制的情况下，三相电压幅值降低至302 V，50 ms后恢复稳定。LQR控制下的逆变器输出三相电压在投入负载后，电压幅值暂降至303 V，经过15 ms就可以恢复稳定。加入性能提升控制结构之后，三相电压的波动幅值大幅降低，波动比例由3%降低至1%以下，15 ms后即可恢复稳定。实验结果表明，LQR+Qc控制策略可以在不改变系统快速性的前提下大幅降低电压波动，提升新型配电系统电压的暂态性能和稳态性能。

图8 阶跃扰动d轴电压波形对比Fig.8 Comparison of step disturbance d-axis voltage waveform

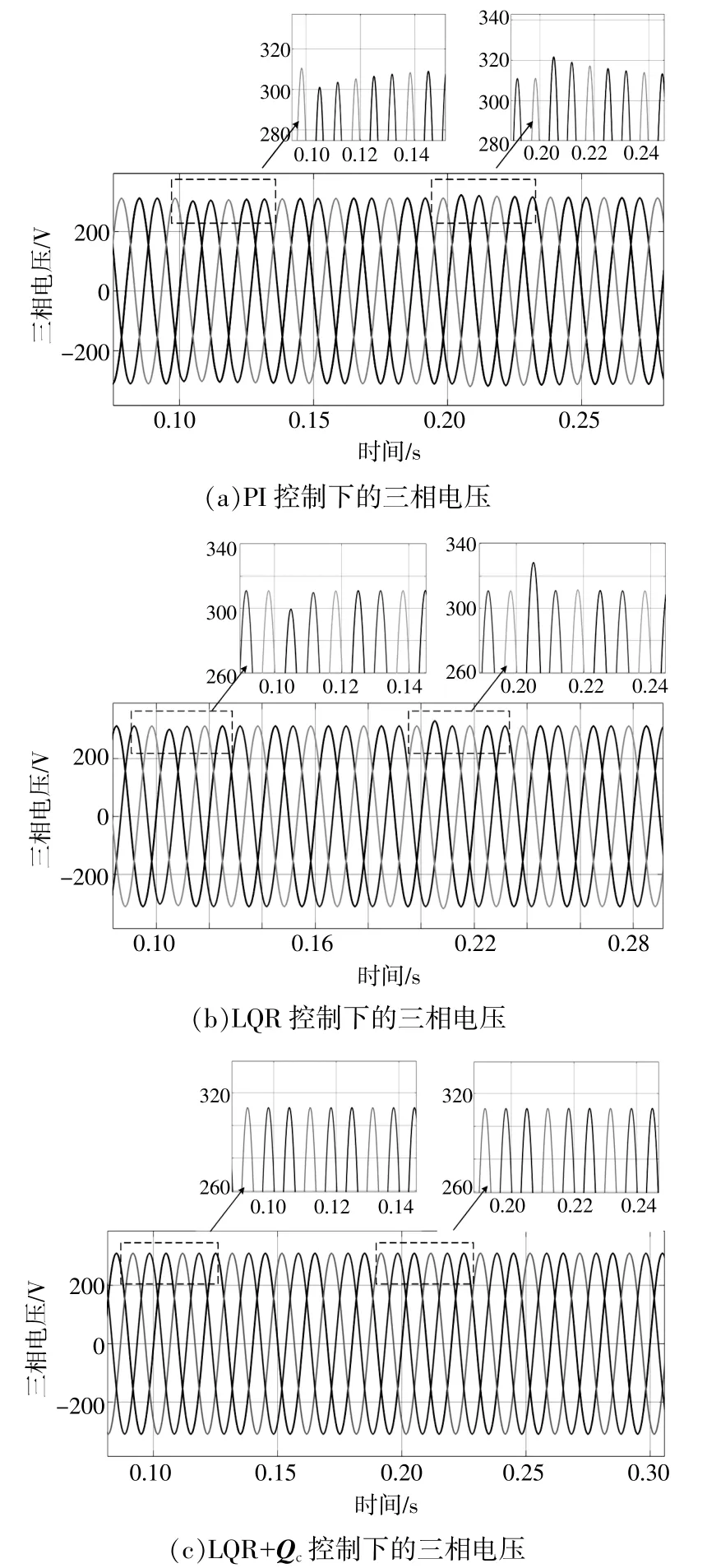
图9 阶跃扰动三相电压波形Fig.9 Step disturbance three-phase voltage waveform

4.2 三相不平衡扰动

在运行中的逆变器上投入不平衡的三相负载，通过MATLAB/Simulink进行仿真验证，得到d轴电压对比波形如图10所示。由图10可以看出，投入不平衡负载后，LQR控制下的d轴电压发生了明显的2倍工频正弦波动，波动幅值为323 V，在加入本文所提的LQR+Qc控制结构后，波动幅值明显降低。

图10 三相不平衡d轴电压波形对比Fig.10 Three-phase unbalanced d-axis voltage waveform comparison

不平衡负载下的三相电压波形如图11所示。在不平衡负载的影响下，三相正弦电压的幅值随三相负载的不同出现了不同程度的变化，幅值分别变为325，305 V和308 V。加入本文所提的LQR+Qc控制结构后，三相电压幅值基本相同，维持在311 V附近。

图11 不平衡负载下三相电压波形Fig.11 Three-phase voltage waveform under unbalanced load

计算三相电压不平衡度，如图12所示。LQR控制下的三相电压不平衡度为4%，加入补偿结构后电压不平衡度降至0.05%。LQR+Qc控制结构可以有效地抑制三相不平衡负载对输出电压波形的影响，提升新型配电系统内电压的可靠性。

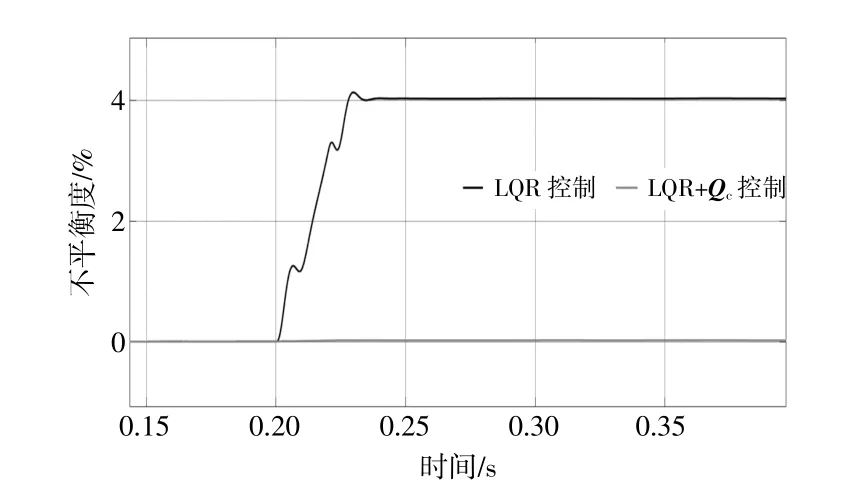
图12 电压不平衡度波形对比Fig.12 Comparison of voltage imbalance waveform

4.3 谐波扰动

谐波扰动主要是由非线性负载造成的，投入非线性负载后可以得到d轴电压对比波形，如图13所示。

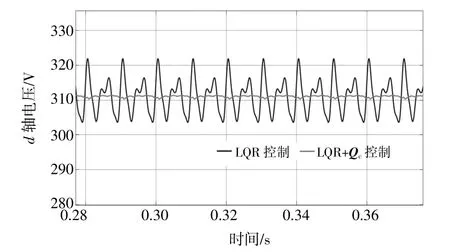
图13 非线性负载d轴电压波形对比Fig.13 Comparison of d-axis voltage waveforms of nonlinear loads

由图13可以看出，加入非线性负载后，在LQR控制下，d轴电压出现了明显的波动，波动幅值为322 V。加入本文所提控制结构之后，d轴电压波动明显改善，幅值降低为311.5 V，抗干扰能力大幅提升。图14为加入非线性负载后的三相电压输出波形。由图14可以看出，三相电压有明显的畸变现象，加入性能提升控制结构后电压波形明显得到改善，接近标准的三相正弦波形。然后利用MATLAB/Simulink自带的FFT对电压进行分析，结果如图15所示。

图14 非线性负载下三相电压波形对比Fig.14 Three-phase voltage waveform comparison under non-linear load

图15 非线性负载FFT分析Fig.15 Nonlinear load FFT analysis

在LQR控制下，逆变器输出电压的畸变率为2.26%，加入性能提升控制结构后输出电压的畸变率降为0.09%。实验表明，性能提升控制结构可以有效地抑制非线性负载对系统电压的影响，提高新型配电系统内电压的鲁棒性和可靠性。

5 结束语

本文在新型配电系统的背景下，选取微电网中的逆变器为研究对象，提出了基于最优控制及扰动残差生成器相结合的逆变器供电性能提升策略，实现了输出电压响应的快速性和抗扰性。通过输出电压和电感电流的状态反馈可以使得逆变器获得良好的动态性能，加入积分控制后可以消除系统的稳态误差，将两者相结合并利用LQR进行求解，使得逆变器启动时电压快速跟随且没有超调，提升了系统的暂态响应速度。当发生扰动时，负载电流作为扰动引起了逆变器输出电压的波动，本文所提的性能提升控制策略在无需额外的电压电流传感器的情况下，快速提取扰动并实现补偿，能够在保证暂态响应速度不变的情况下提高逆变器的抗扰能力，提升新型配电系统中电压的鲁棒性。